高铁锻钢制动盘热疲劳裂纹扩展仿真及寿命评价

王连庆，吴圣川，胡雅楠，秦庆斌，钱坤才

(1.北京科技大学 新金属材料国家重点实验室，北京 100083；2.西南交通大学 牵引动力国家重点实验室，成都 610031；3.中车戚墅堰机车车辆工艺研究所有限公司，常州 213011)

1 引 言

高速列车普遍采用摩擦盘形制动装置。随着运行速度的提高，制动负荷及热能呈现几何级增长，必然使制动盘局部区域产生超常热点。反复制动后会导致热疲劳、氧化和磨损等损伤，一般表现为盘面中心区出现网状的径向热疲劳裂纹[1]。微裂纹缓慢增长并逐渐汇聚为一条主裂纹，扩展至一定尺度后，便导致整个制动盘的断裂失效，严重危及乘客生命财产和行车安全[2]。

对在役制动盘进行无损探伤，探索热疲劳开裂行为及其演变机制，有利于厘清制动盘不同服役工况下的运用情况，为制定合适的检修周期和判废限界提供重要的理论依据[2，3]。然而，制动盘的高速转动使得实验技术很难准确测定热斑和热裂纹的形成区间，并且实验数据稀缺，代表性严重不足，更无法实时追踪缺陷空间演化行为[4-6]。

另一方面，采用数值方法能够高效地重建给定制动工况下制动盘中热应力场的演变规律，结合制动盘材料的疲劳断裂参数，得到裂纹尖端场的应力强度因子，估算出剩余寿命，已成为当前制动盘损伤容限分析的首选方法[7,8]。

必须指出，传统数值方法基于小变形理论进行热应力场研究。以往方法在进行热裂纹扩展仿真中，裂纹每扩展进一步，制动盘的几何模型、单元网格、材料属性、载荷和边界条件等均需要重置，这就导致传统方法的计算效率、精度和收敛性较低，在产品设计和工程运用中进展缓慢[8,9]，因此尚不能对更高速度级高铁制动盘的损伤容限设计和剩余寿命评估提供直接的科学支撑。

以下一代高速列车锻钢制动盘面的径向热裂纹扩展为对象，实验获取热疲劳断裂参数，模拟出制动热力耦合过程，在铁路车辆关键基础部件损伤评价领域，采用扩展有限元法(XFEM)和自主研发的虚节点多边形单元(VPM)的自适应加密进行三维热疲劳断裂仿真[10,11]，得到径向热裂纹扩展的寿命曲线。研究结果为制定新型国产锻钢制动盘的探伤周期决策提供了理论依据。

2 理论模型

制动热能通过盘体与环境的热传输实现能量转化，并在盘面形成热斑和严重的应力集中。这种急剧的循环热机耦合过程是导致制动盘热疲劳开裂的根本原因[12,13]。本文基于线弹性断裂力学理论，以应力强度因子表征热裂纹尖端奇异场强度，建立基于热力耦合场的裂纹扩展模型。

2.1 能量平衡方程

考虑弱热力耦合的三维瞬态热系统，各项同性材料中某点x在笛卡尔坐标系的温度可由能量平衡方程和边界条件得到[8，10]，即

(1)

(2)

(3)

(4)

式中k为热传导系数,Qv为热生成,n为单位向量,Ta为远场环境温度(令初始温度为25 ℃),热流密度qn由制动摩擦能量换算得到,并作为Qv的热输入,假设制动盘边界温度为T0。

为简化计算和便于编程,总散热损失系数he包括对流换热系数hc和热辐射系数hr,即[9]

hc=0.036Pr1/3λ[(u∞·L/γ)0.8-23500]/2πr

(5)

(6)

式中Pr为常数,r为盘面半径,ε为发射系数,λ为热导率,γ为动力粘度,σ为玻尔兹曼常数,L为制动盘周长,盘面空气流速u∞由线性插值得到,与列车速度的关系曲线如图1所示[14]。

根据图1得到对流换热系数,与辐射换热系数叠加得到等效换热系数,如图2所示[8]。

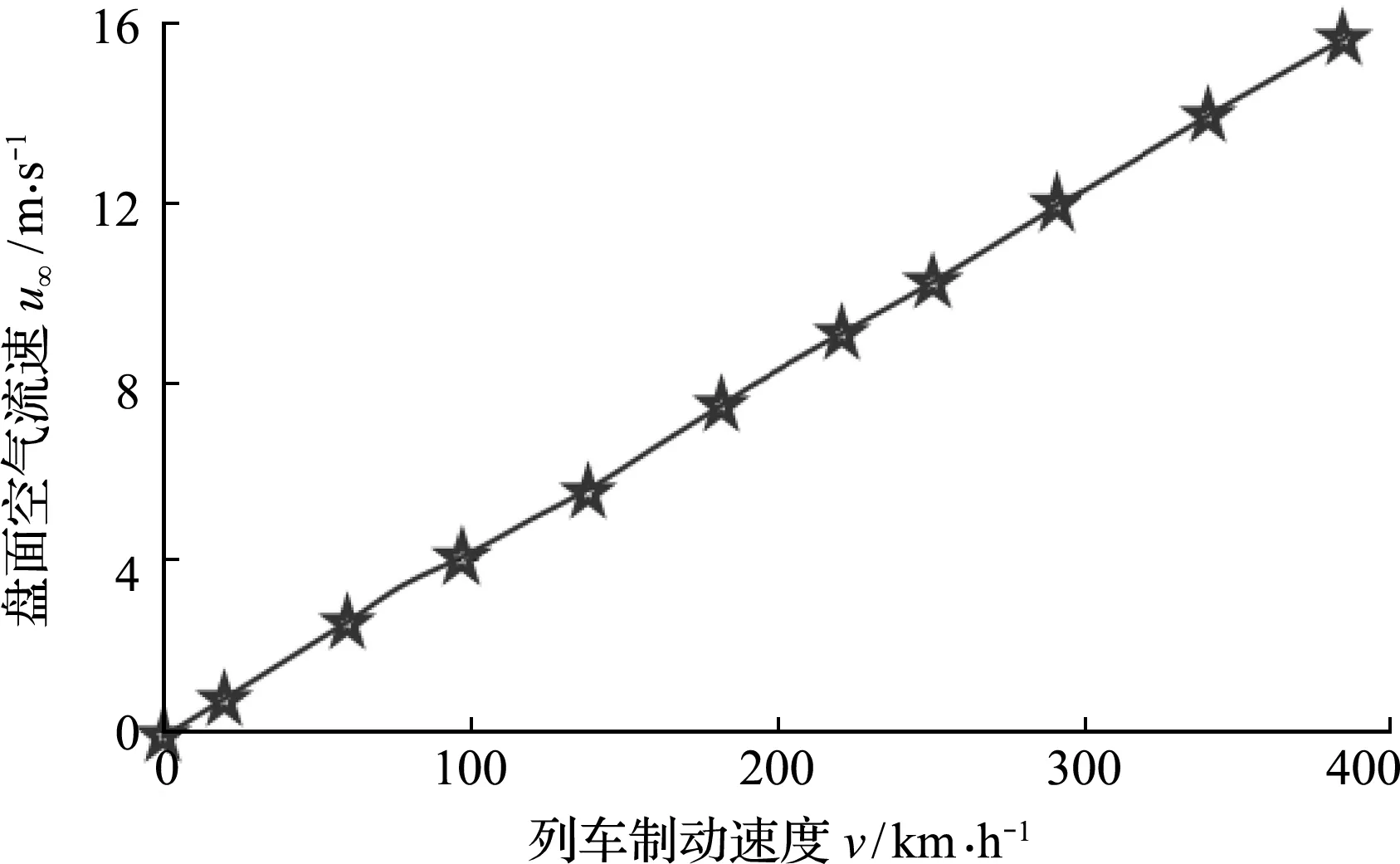
图1 盘表面上空气自由流速变化

2.2 制动能量转换

由于形式简洁和精度较高，能量转换法在制动盘热机分析中应用广泛[5]。为此,本文采用能量转换法估算式(1)所示内能,有

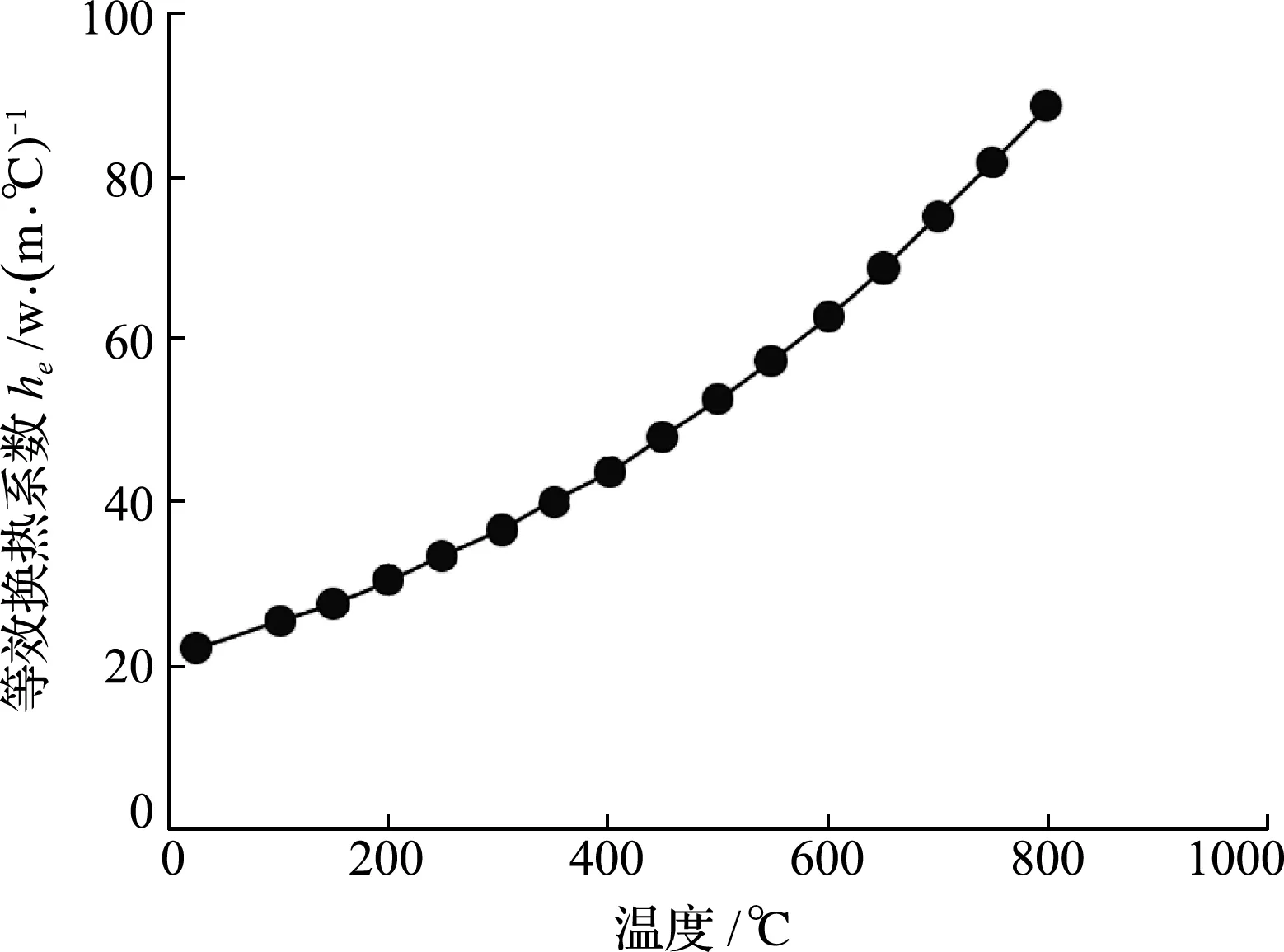
图2 等效换热系数与温度关系

(7)

设列车前进方向为x轴,当匀速行驶进行正常制动时,热流密度由式(8)计算得到。

(8)

式中a和v0分别为制动加速度和制动初速度。

2.3 热弹性应力场

设应变张量ε和柯西应力张量σ与温度变化呈比例关系,则

(9)

ε=su，σ=D·ε0

(10，11)

式中I和D分别为单位向量和弹性矩阵,α为制动盘材料的热扩展系数。把瞬态温度场作为载荷条件代入式(9～11)即可得到制动盘的热应力场。单一问题域Ω内热弹性问题的控制方程和相应边界条件为

(12～14)

式中b，u0和p分别为体积力(=0)、对称边界位移条件(=0)和制动闸片的压力。

3 基于XFEM的热裂纹扩展

传统有限元法基于小变形假设,无法高效求解动态裂纹问题,其根本原因是动态裂纹面与结构模型不能保持独立。基于单位分解原理,通过富集经典有限元的位移模式,Mo⊇s等[15]发展了著名的扩展有限单元法,已成为当前求解不连续问题最有效的数值方法之一[16,17]。

但XFEM对求解精度和效率的改善效果较差。为此,本文基于提出的VPM算法实现了裂纹尖端分层加密和网格松弛技术(图3),并据此开发出一款三维裂纹扩展分析商业软件[11,18]。本文将进一步发展热疲劳开裂问题,从而为在役结构无损检测周期方案的制定提供理论支持。

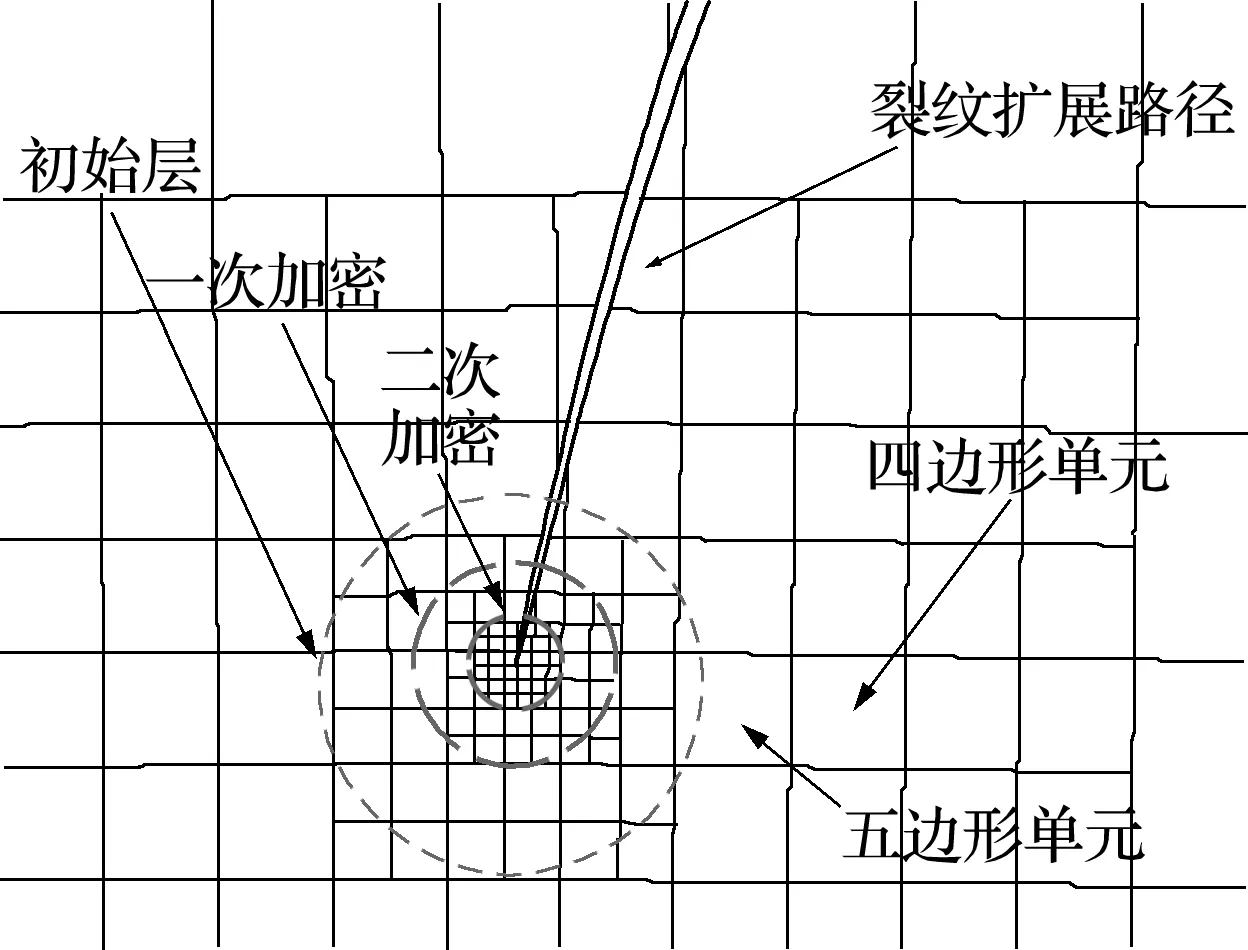
图3 裂纹尖端分层加密示意图

根据图3,瞬态温度场和位移场将分别在裂纹尖端处进行重构[18，19],即有

(15)

(16)

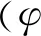
大队学校也开学了。大水淹死了三个老师，表姐补了上去。杆子说，还是有文化好啊，国家惦着你们哩。上面扒来扒去，大队就剩你小水是刚下学的初中生了。

(17)

式中θ和r为以裂纹尖端为中心的极坐标。

张开型裂纹是理论和工程研究中最危险但最常见的一类断裂问题。制动盘为I型裂纹为主的失效模式,为此还计入了II型裂纹贡献。则裂纹扩展方向θc和裂尖等效应力强度因子Ke为

(18)

(19)

4 热疲劳开裂XFEM模型

根据国家标准《GB/T 6398-2017金属材料疲劳裂纹扩展速率试验方法》和《GB/T 21143-2014标准金属材料准静态断裂韧度的统一试验方法》在图4所示锻钢制动轴盘上沿着轴向截取断裂力学试样,实测高温下应力比为-1的经典Paris曲率中常数C和m、断裂韧度KI C和门槛值ΔKt h。

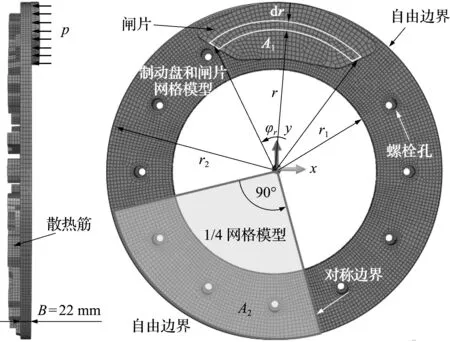
图4 三维热疲劳裂纹计算网格模型及参数

4.1 材料抗热开裂属性

制动盘在经历奥氏体化、淬火、回火和空冷处理后,锻钢材料的室温强度达到1000 MPa。由于制动峰值温度达到700 ℃,需要测定高温区的热物性参数[5,10]和抗疲劳断裂属性列入表1。

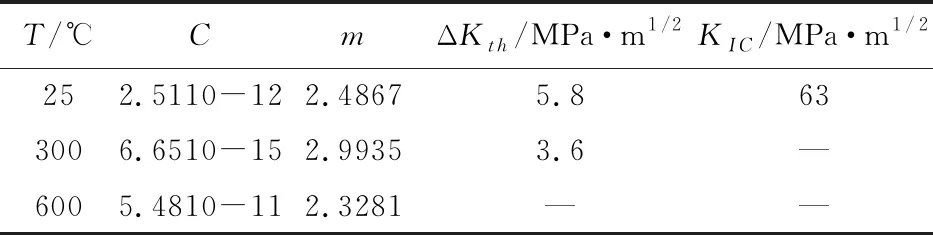
表1 制动盘不同温度下的开裂参数

4.2 三维网格模型

图4为温度场、热应力场和三维热疲劳裂纹的仿真网格模型及边界条件和几何参数。

可以看出,首先在Hypermesh中剖分好三维实体网格(六面体单元C3D8,总节点数为27025,单元数为22260),然后在ABAQUS软件中进行温度场分析。用Г0，Г1，Г2和Г3分别表示温度边界、热流输入边界、对流边界和热辐射边界。考虑到结构对称性,取图4的1/4为计算模型。

表2为几何参数和制动条件,用以模拟行车速为400 km/h下制动热损伤演变规律。

表2 制动盘的计算模型参数

4.3 失效判据

考虑到裂纹扩展计算和评估方法的局限性,本文主要考察单个主裂纹。多裂纹和短裂纹问题仍是一个极具挑战性的课题[2]。

工程中,目视检查摩擦面或者加工面的失效判据如下。(1) 裂纹底部点和表面两点的最大应力强度因子值Kmax>KI C； (2) 盘面上裂纹总长度大于100 mm； (3) 裂纹尖端距离盘体边缘大于 10 mm；(4) 深度a大于制动盘厚度B。

此外,对于非摩擦面或者孔边的裂纹容限尺寸,与此并不相同,需要根据制动工况以及具体的制动盘的结构形状进行综合分析。

5 结果与讨论

5.1 热斑的形成

图5为制动185 s后的温度场。可以看出,制动初速度为400 km/h开始仅制动,至185 s时在制动盘两孔间形成一个最大的宏观热点或热斑,峰值温度约为681.2 ℃,这与现场实测温度及分布基本一致。

5.2 热疲劳开裂应力场

仿真和实验均表明,在热点处会形成热损伤和热裂纹[5，7-10]。据此在图5的热点处插入半椭圆表面裂纹,基于XFEM进行热裂纹扩展仿真。图6给出了失效阶段的裂纹尖端应力场[8]。可以看出,应力最大区始终位于裂纹尖端。考虑到制动盘热裂纹主要沿着径向扩展,而摩擦片运动方向和最大摩擦力均垂直于裂纹扩展方向,因此认为制动盘热疲劳失效应为I型裂纹张开模式为主和其他裂纹扩展模式为辅。为了方便表征裂纹尖端的热应力场强弱,采用第一主应力和式(19)得到等效应力强度因子幅值ΔKe。根据表1不同温度下Paris公式常数C和m,基于式(20,21)获得一个循环后表面和内部最深点的裂纹长度。

ai=ai - 1+C(ΔKi - 1)m

(20)

cj=cj - 1+C(ΔKj - 1)m

(21)

以上方程用于裂纹扩展判据,若有任一计算的裂纹长度满足4.3节的失效判据,则即可停止计算。设裂纹扩展增量为0.5 mm为计算步,对于裂长度2c在2 mm～132 mm积分得到循环周数。

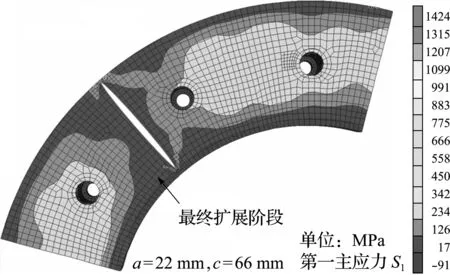
图6 裂纹尖端第一主应力场

图7给出了列车总制动次数或者循环周数与裂纹表面长度之间的关系曲线[8]。研究发现,对比4.3节所述(1)、(3)和(4)均未超出限制,当裂纹长度超过100 mm时认定制动盘报废,据此得到初速度400 km/h时制动总次数约276710。假设每天制动为50次,安全系数取3.0,换算出该制动盘可以正常运行5.1年。这一预测基本符合实际锻钢制动盘的平均运用寿命。

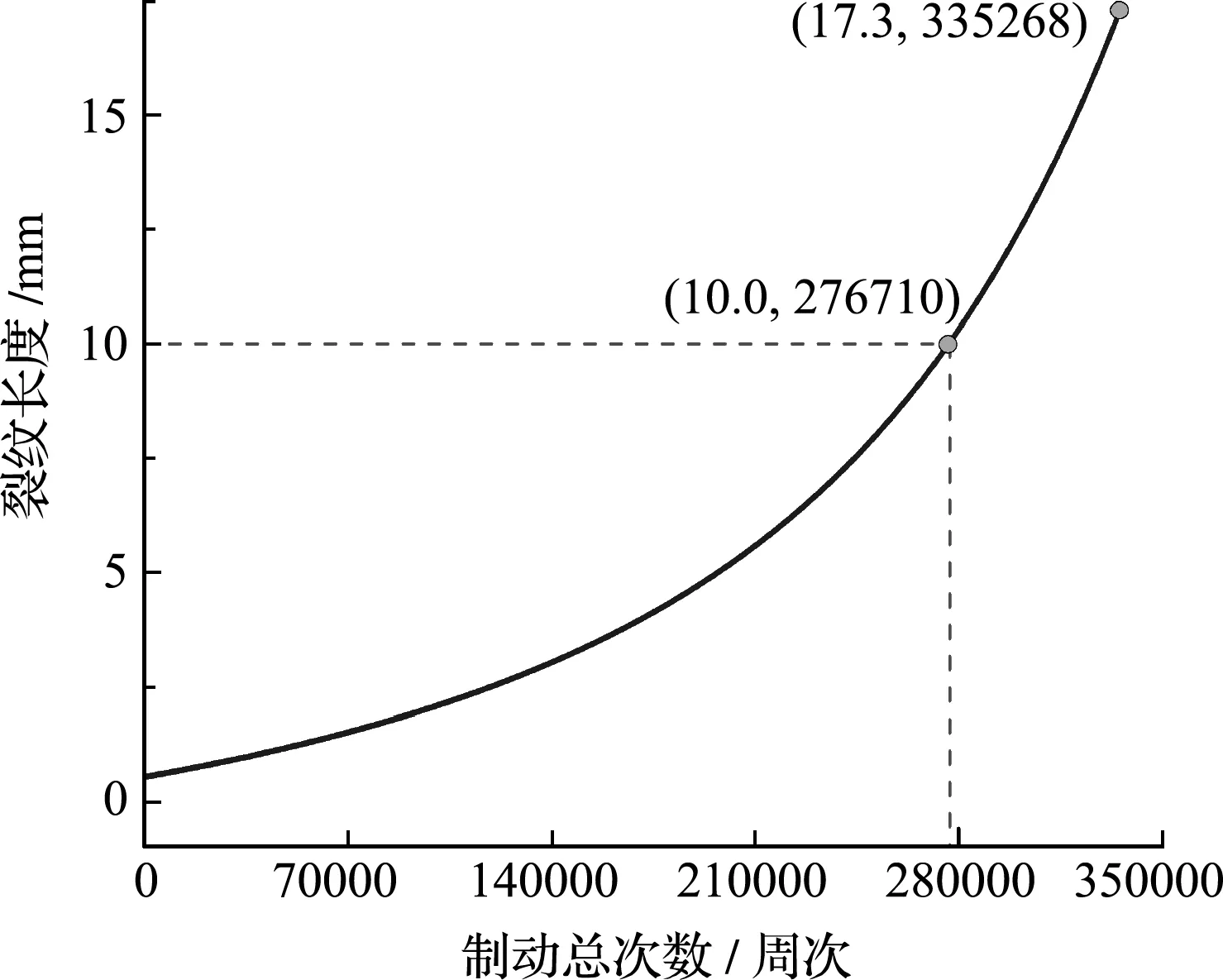
图7 制动总次数与裂纹长度的关系

6 结 论

本文基于新型裂纹扩展算法XFEM和自主研发的多边形单元加密VPM技术,结合制动盘检测限值2 mm和材料的抗疲劳开裂属性,在热点区域插入半椭圆表面裂纹,预测得到初速度为 400 km/h 锻钢制动盘的服役寿命,结论如下。

(1) 温度峰值与实测基本一致,表明能量折算法及边界条件设置合理、可行且有效。

(2) 宏观热点位于两个散热孔间偏向盘面外缘位置,同时还存在多个小的热点区域。

(3) 裂纹主要沿着径向扩展,400 km/h初始制动速度下能够正常使用5.1年。

为确保制动盘损伤容限分析的准确性、可靠性与有效性,下一步研究中有必要对制动闸片接触摩擦以及结合空气动力学仿真结果考察制动温度场和热应力场的时变演化行为。此外,准确地测定出高温区制动盘材质的力学性能尤其是热疲劳开裂性能参数迫在眉睫。最后,本文虽然测定了应力比R=-1的热疲劳断裂参数,但仍然基于Paris方程进行剩余寿命预测,所得结果偏于安全。在未来研究中,有必要综合考虑塑性致裂纹闭合和氧化膜致裂纹闭合效应对裂纹扩展模型进行改进。