正交各向异性加筋板屈曲分析方法研究

黄丽华，刘鹏洋，曲激婷

(大连理工大学 建设工程学部，大连 116024)

1 引 言

复合材料薄壁加筋层合板结构具有比强度高、比刚度大和可设计性强等显著优点，在航空航天和工业建筑等工程领域得到广泛应用。该类薄壁加筋构件最常见的失效模式为屈曲，开展此类结构的稳定性计算方法研究具有实际意义和应用价值。

针对正交各向异性薄壁加筋板的稳定性计算问题，国内外学者开展了大量研究。刘腾喜等[1]用混合硬化正交各向异性塑性理论和屈曲的能量法则，推导了正交各向异性薄板在面内压缩下的弹塑性稳定方程。刘从玉[2]在筋条与壁板之间引入界面单元及罚刚度，研究了加筋板前后屈曲行为及筋条与壁板之间的脱粘现象。曲文斌等[3]利用有限元软件模拟了各种边界条件和荷载作用下正交各向异性板的屈曲失稳形式。杨端生等[4]根据各向异性矩形薄板剪切屈曲横向位移函数的微分方程建立了一般性的解析解。刘毅等[5]将加筋板简化为受弹簧约束的层合板，利用伽辽金法得到屈曲与后屈曲解析解。王春玲[6]讨论了正交各向异性板在面内边界力作用下的屈曲和后屈曲行为。Mittelstedt[7,8]推导并求解了对称轴压荷载作用下加筋板的弹性屈曲荷载理论解;此外，采用半解析法推导了单筋加筋板在压剪复合荷载作用下的屈曲荷载理论解。Byklum等[9]引入几何非线性，分析了双向加筋板在双向轴压载荷下发生局部屈曲的前后屈曲行为。 Brubak等[10]用半解析法对带有任意方向筋条的加筋板在压剪载荷下的前后屈曲行为进行了分析。Kharazi等[11]采用里兹法，基于一阶剪切变形理论并结合多项式级数得到位移场，对板的稳定性问题进行分析。杨俊清等[12]将正交各向异性矩形层压板的剪切屈曲荷载计算公式应用于预测试验屈曲荷载。徐元铭等[13]基于假设提出了一种对于四边简支矩形次加筋板的屈曲荷载近似计算方法。刘文庆等[14]提出了复合材料层合板等效材料力学参数公式。汪厚冰等[15]对帽型加筋板的剪切屈曲荷载进行理论分析及数值模拟，推导了蒙皮应变分布，并基于半经验和理论公式计算出剪切屈曲荷载。

为简化正交各向异性薄壁加筋板的稳定性计算，本文基于里兹法，推导板和筋条的总势能，基于最小势能原理，建立不同压剪比复合荷载作用下正交各向异性加筋板的弹性稳定性控制方程，进而针对单筋和三筋加筋板开展屈曲荷载及模态分析。

2 理论推导

任意正交各向异性加筋板及筋条坐标系如图1所示。

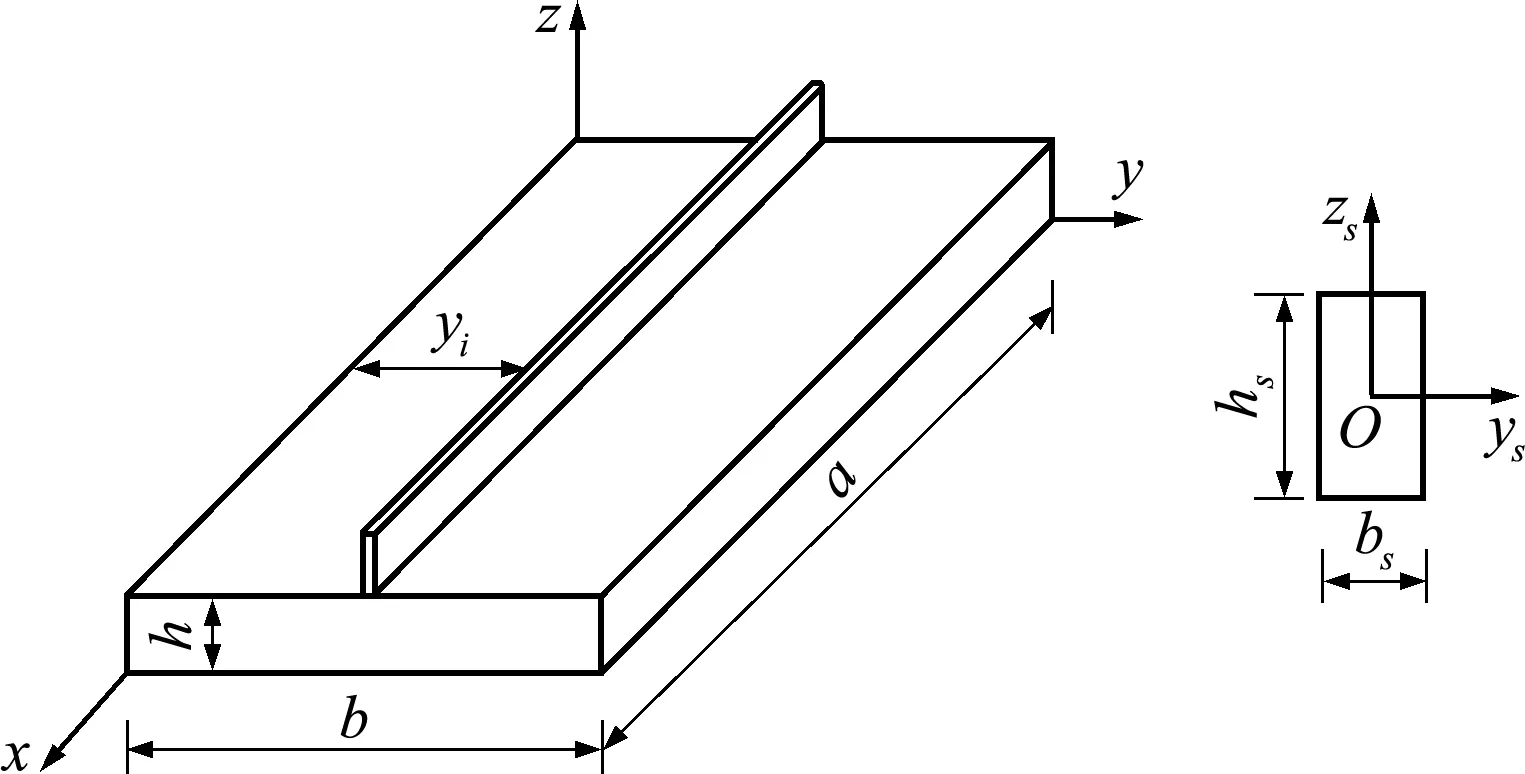
图1 加筋板及筋条

设u，v和w分别为薄壁层合板中面x，y和z三个方向的位移，根据基尔霍夫假设，薄板内任一点位移场表达为

u(x,y,z,t)=u0(x,y,t)-z∂w0/∂x

v(x,y,z,t)=v0(x,y,t)-z∂w0/∂y

w(x,y,z,t)=w0(x,y,t)

(1)

由格林应变张量得弹性体的应变与位移关系

(2)

根据小变形假设，忽略式(2)的u和v二次项，计横向法线的偏转角度，将位移场表达式(1)代入式(2)，可得到von Karman应变位移假设，

(3)

正交各向异性板的应力-应变关系为

σx=Ex(εx+εyνy x)/(1-νx yνy x)

σy=Ey(εy+εxνx y)/(1-νx yνy x),τx y=Gx yγx y

(4)

式中Ex和Ey为x和y方向弹性模量，νx y和νy x为主副泊松比，Gx y为剪切模量。将式(3)的非线性应变位移关系线性化，与式(4)一同代入应变能的计算公式，得正交各向异性板应变能表达式为

(5)

式中各系数的表达式如下，h为板厚。

筋条坐标系ysOzs如图 1所示。设沿x方向上固定第i个筋条，将筋条简化为附着在板上的梁，根据梁和板在连接处位移协调，梁内任意点位移场与连接在板上的点的位移关系表达式为

zs[∂w(x,yi,t)/∂x]

zs[∂w(x,yi,t)/∂y]

(6)

式中偏心距ex i=(hs+h)/2，hs和bs为筋条高度及宽度。

根据加筋条内部位移场表达式(6)，结合应变位移关系式(3)，得到由板中面位移表示的加筋梁应变位移关系式为

(7)

由此正交各向异性筋条的势能表达式为

(8)

薄板面内载荷在位移上所做的功为

(9)

式中Nx x和Ny y分别为x和y方向的面内力,Nx y为剪切力。由此，正交各向异性加筋板的总势能为

(10)

四边简支约束时，满足边界条件的位移函数为

(11)

式中Ai j，Bi j和Ci j为待定系数，a和b分别为板在x和y方向的几何尺寸。将式(11)代入总势能方程(10)，由最小势能原理,得到齐次线性方程组的矩阵表达式为

(12)

由此可得正交各向异性加筋板在压剪荷载下屈曲分析的控制方程。其中第一个方阵为正交各向异性板的线性刚度阵，矩阵中各项表达式如下。

第二个方阵为正交各向异性筋条的线性刚度阵，矩阵中各项具体表达式如下。

式(12)等号右侧的方阵为沿x方向轴压荷载、面内剪切力及沿y方向的轴压荷载作用下的刚度矩阵，具体表达式如下。

由此可得关于Ai j,Bi j和Ci j的齐次方程。使用Matlab编程，采用梯形trapz函数进行数值积分，计算特征值及特征向量，即得到正交各向异性加筋板的特征值屈曲荷载及对应的屈曲模态。

3 实例分析

3.1 模型参数

如图2所示，取边长a×b=1 m×1 m，厚度h=0.01 m的正交各向异性加筋板，筋条厚度bs=0.029 m，筋条高度hs=0.04 m，板和筋条由同种正交各向异性材料构成，材料性能分别为Ex=133 GPa，Ey=10.4 GPa，Gx y=4.14 GPa，νx y=0.29。

加筋板在平行于筋条方向上受到对边施加的轴压荷载，沿四边方向受到剪切荷载，如图3所示。取压剪比为1∶1，5∶1和1∶5，分别计算四边简支的正交各向异性加筋板在复合荷载作用下的屈曲荷载及屈曲模态。工况1，筋条位于yi=0.5 m 处；工况2，筋条分别位于yi=0.25 m，0.5 m，0.75 m 处。

3.2 计算结果分析

将上述参数输入到Matlab程序中，同时使用Abaqus有限元软件，建立有限元模型如图4所示。

图2 几何示意图

图3 边界条件及荷载

在有限元分析中，固定四个侧边所有节点的w方向位移，以及垂直于筋条方向侧边的y方向位移，实现四边简支的边界条件。沿x方向施加轴向载荷，四边施加剪切载荷。

工况1： 单筋板在三种压剪比下，前五阶屈曲荷载及屈曲模态计算结果列入表1和表2。

工况2： 三筋板在三种压剪比下，前五阶特征值屈曲荷载及模态计算结果列入表3和表4。

由表1和表3可知，单筋加筋板在三种压剪比下，一阶屈曲荷载值较小，故相对误差略大，最大误差为6.41%，三种荷载下前五阶屈曲荷载值的平均相对误差分别为3.39%，2.12%和1.47%。三筋加筋板在三种压剪比下，一阶特征值屈曲荷载相对误差较大，最大为10.55%，三种荷载下前五阶屈曲荷载值的平均相对误差分别为4.30%，5.40% 和 4.27%。整体而言，当压剪比为1∶1时，各阶屈曲荷载值均最小，故在实际应用中应尽量避免加筋板构件受到压剪比相近的复合荷载。随着筋条数目增加，屈曲荷载平均增加28%左右，三筋加筋板前五阶特征值屈曲荷载的相对误差均比单筋加筋板的相对误差大2.3%左右。

图4 有限元模型

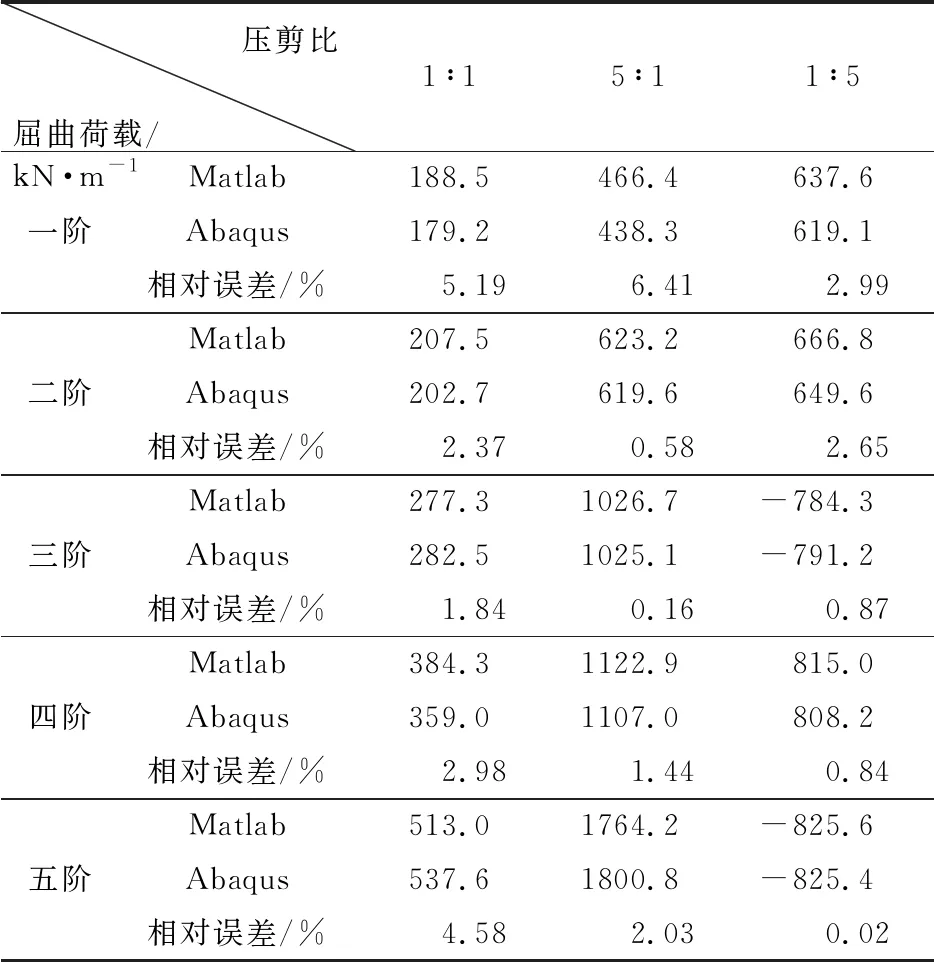
表1 屈曲荷载计算结果对比

由表2和表4可知，三种压剪比下前5阶模态呈反对称形式，三筋加筋板与单筋加筋板前3阶模态差异较小，可见筋条数目对于屈曲模态影响较小。压剪比为1∶1的屈曲模态与压剪比为5∶1的屈曲模态相似，说明轴压荷载主导了屈曲模态。基于本文算法得到的两种工况的三种复合荷载下的前五阶特征值屈曲模态与Abaqus软件计算结果基本一致。个别模态存在细微差别，主要原因在于，本文计算单筋、三筋加筋板所取位移函数的阶数上限分别为11阶和13阶，上限值越大，计算得到的屈曲荷载及模态越精确，但相应的计算量也越大；此外，本文仅考虑面内荷载对薄板做功，而忽略外荷载对筋条做功，导致结果误差，筋条越多误差越大。

表2 屈曲模态计算结果对比

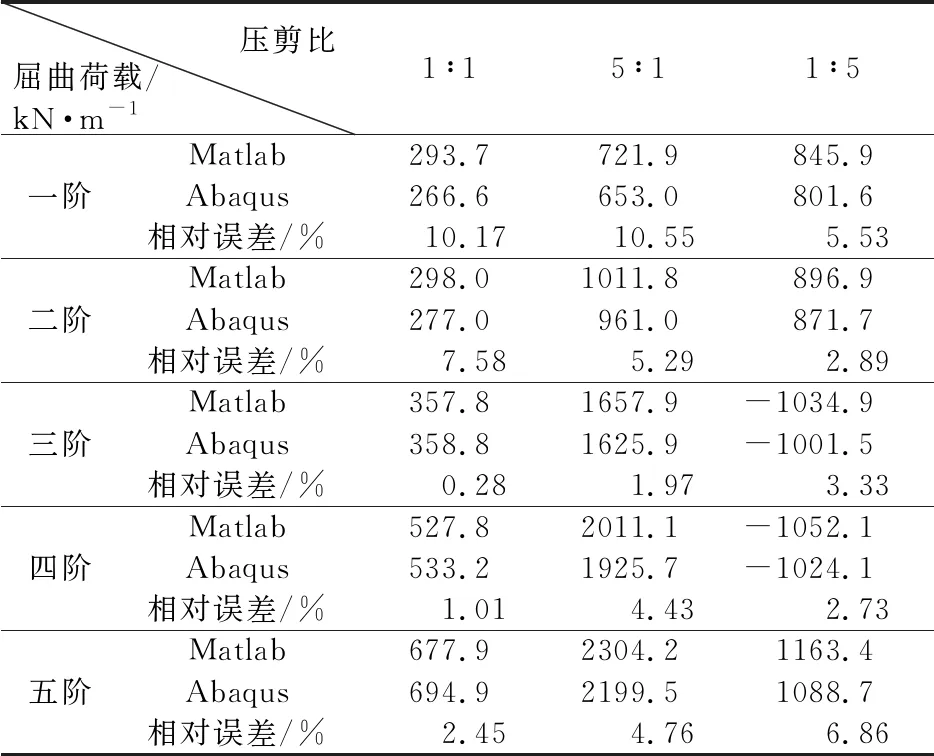
表3 屈曲荷载计算结果对比

表4 屈曲模态计算结果对比

4 结 论

本文基于里兹法推导了正交各向异性加筋板屈曲分析的控制方程，采用Matlab计算加筋板的屈曲荷载和屈曲模态。通过计算单筋和三筋加筋板在三种不同比例的压剪复合荷载下前五阶屈曲荷载及模态可知，当压剪比为1∶1时，各阶屈曲荷载均最小，故在实际应用中应尽量避免加筋板受到压剪比相近的复合荷载；筋条数目由1根增加到 3根后，屈曲荷载平均增加28%左右，计算相对误差平均增大2.3%，计算精度可通过增加位移函数阶数提升。基于本文推导的正交各向异性加筋板弹性屈曲解，能够得到较精确的特征值屈曲荷载及对应模态。