行星架应变片粘贴与标定

郑晖，冯金，覃琨，刘晓凡，李嘉东

（中国航发商用航空发动机有限责任公司 机械系统部，上海202007）

0 引言

齿轮传动系统是机械传动系统中最重要而且应用最广泛的运动装置，星型齿轮传动是航空发动机上常用的一种功率分流齿轮系传动，其结构如图1所示。由于星型齿轮传动结构采用定轴轮系，其系统刚度、强度和工作可靠性都较高，一般适用于航空减速器。星型轮系的传动路径是从太阳轮经行星轮到内齿圈，依靠多个行星轮将轮系的动力分流传动，行星架则作为固定机构，将齿轮啮合产生的转矩传递到传扭支架上。

当星型轮系由于加工误差和装配误差产生不均载现象时，会导致系统应力分布不均，从而产生振动、噪声、降低齿轮寿命等影响，降低了系统的性能和效率。对星型齿轮传动系统动态不均载特性进行计算分析，有助于进一步地了解系统的传动动态特性和均载特性，提高齿轮箱稳定性、寿命和效率。

目前国内很少有对行星架应变片的粘贴和标定方法方面的研究，大多数研究都集中在使用有限元软件对风电齿轮箱和大型机械设备使用的减速器行星架进行分析。通过理论的计算与试验的数据，使用软件模拟行星架在齿轮传动系统在实际运转过程中的受力情况和边界条件，得出行星架的应力和应变分布，从而对行星架进行优化处理[1-3]，但是国内并没有对行星架均载试验过程中均载系数进行计算和监测的方法。

图1 星型齿轮传动结构图

本文通过有限元分析与应变片粘贴的方式对行星架每个轴孔的受力情况进行分析与验证。首先通过ANSYS软件对行星架进行有限元分析，确定应变片粘贴的位置，将应变片贴至轴孔受力最大处，将补偿片贴至轴孔受力最小处，并使用工装对应变片进行标定，最后得出拉力与应变的关系进行分析。标定完的应变片可以在试验过程中通过数采设备获得应变数据，从而可以算出行星架每个轴孔在特定时刻（使用静态数采设备）或者特定时段（使用动态数采设备）的均载情况，对星型轮系的合理设计与成功使用具有重要意义。

1 位置选择

1.1 理论分析

使用有限元分析软件对行星架实际受力情况进行模拟，5组轴孔分别受到来自行星轮轴的周向力，所有孔的内外表面受力情况如图2所示。行星架5个轴孔上下表面处，沿受力方向靠近轴孔边缘处应力都较大，逆着受力方向靠近孔边缘处和行星架边缘处应力都较小。

1.2 位置选取

行星轮轴与行星架为小间隙配合，在转动方向不变的情况下，齿轮啮合对行星架产生的周向力会使行星轮轴只有一侧与行星架接触，另一边不接触。结合有限元静力计算分析，行星架上单个轴孔受到应力最大处在沿着受力方向经过轴孔圆心的连线上。在沿着行星架轴孔的受力方向不同距离的上下端面处粘贴多组应变片，大致位置如图3所示，使用工装对行星轮轴孔施加拉力。试验测得，2号、9号和11号应变片位置处应力变化的线性度较好。所以最终将沿着受力方向且过圆心的线上选取最靠近轴孔的一点作为贴片点。

图2 行星架受力有限元模拟结果

图3 应变片位置选取

在行星齿轮箱实际运转过程中，系统由于摩擦会产生大量的热量，润滑油和油雾会使系统温度上升。材料会随温度上升而膨胀，导致应变片测量结果偏大。因此，在行星架应力最小且距离应变片距离较近处需要粘贴补偿片，补偿片会补偿应变片由于温度而产生的误差。由于行星架受到的转矩是沿着切线方向的，所以补偿片的位置选定在垂直于受力方向且尽量靠近应变片的位置。最终，补偿片粘贴在轴孔与内孔圆心的连线上且在轴孔和外圆之间。

行星架上每个孔的内表面在选取的粘贴点水平粘贴了3个应变片作为工作片，再贴了3个应变片作为补偿片与3个工作片一一对应。行星架孔1应变片和补偿片的粘贴位置如图4所示，应变片和补偿片编号从外向内依次为1号、2号、3号。行星架孔1应变片和补偿片的粘贴位置如图5所示，应变片和补偿片编号从外向内依次为1号、2号、3号。2号与4号工作片与补偿片距离行星架轴孔中心的距离都约为60 mm。

2 试验方法与过程

此试验需要设计一套工装，要求工装有一根工装轴可以施加沿轴孔实际受力方向的拉力并将所有受到的力传递到行星架轴孔上，工装还需要有4根工装轴将行星架定位并将受到的力全部传递到铸铁平台上。

图4 行星架孔1应变片实际贴片位置与编号方法

图5 行星架孔2应变片实际贴片位置与编号方法

行星架应变片标定工装如图6所示，底座由螺栓安装在铸铁平台上，垫板由螺栓安装在底座上，支撑座和盖板由螺栓安装在垫板上。行星架安装在支撑座内并由定位轴安装在垫板上，施力轴安装在行星架上且不与垫板接触，牵引杆与拉杆通过键槽定位安装在施力轴上，施力轴截面图如图7所示。

试验时在拉杆上施加拉力，拉力通过施力轴全部作用在行星架上，拉力方向与星型齿轮系统受力方向相同。此试验采用手拉葫芦施加拉力，使用标定过的电子吊秤来读取拉力。现场安装照片如图8所示，由于安装空间不足和精度问题，定位轴只安装了2根。

标定开始前，首先施加适当的拉力，去除行星架与工装的残留应力和安装间隙。试验开始时，先将铁链保持在松弛状态，待电子吊秤读数为0时，采集第一组数据确保应变片为不受力状态。随后拉动手拉葫芦，依次增大拉力至1000、2000、3000、4000、5000、6000、7000 kg，待每个测量点读数稳定后停留至少2 min再采集应变片数据。然后从7000 kg减少拉力至1000 kg，并每隔1000 kg待拉力稳定后采集应变片数据。为了使数据有对比性，在拉力减少至1000 kg后，继续加载到7000 kg最后卸载到1000 kg，并每隔1000 kg待拉力稳定后采集应变片数据。做完行星架上一组孔后，旋转行星架，使用相同的方法采集其余4组轴孔上应变片拉力与应变片读数。

图6 行星架应变片标定工装示意图

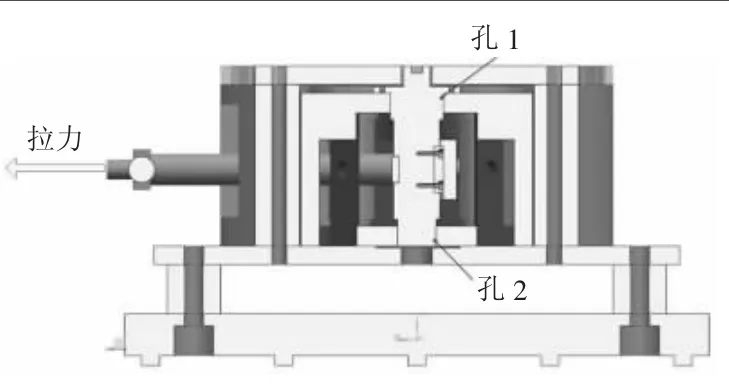
图7 行星架应变片标定工装施力轴截面图

图8 行星架应变片标定工装整体照片

3 试验结果分析

3.1 试验数据

由于行星架每组轴孔都有6组应变片，且需要完成2次加载和2次卸载，总计840个数据点。本文挑取了一组轴孔应变片数据进行分析，2次加载与卸载的数据如表1～表4所示。

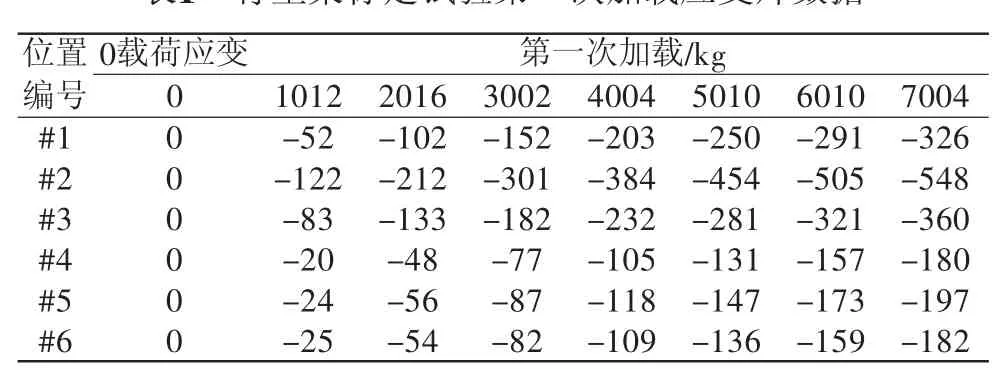
表1 行星架标定试验第一次加载应变片数据

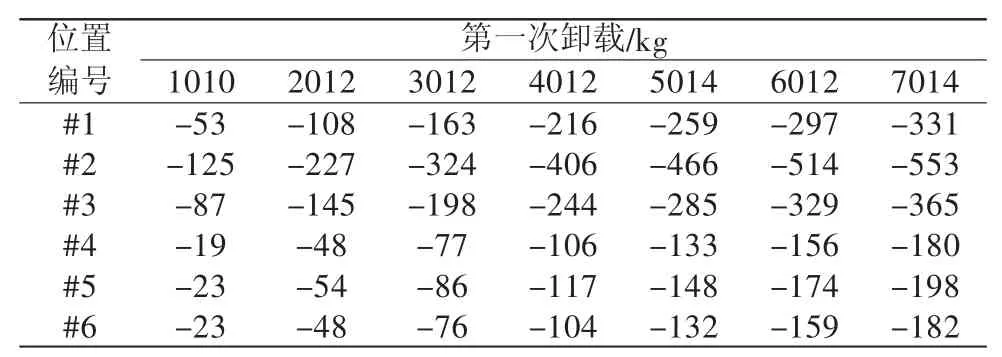
表2 行星架标定试验第一次卸载应变片数据

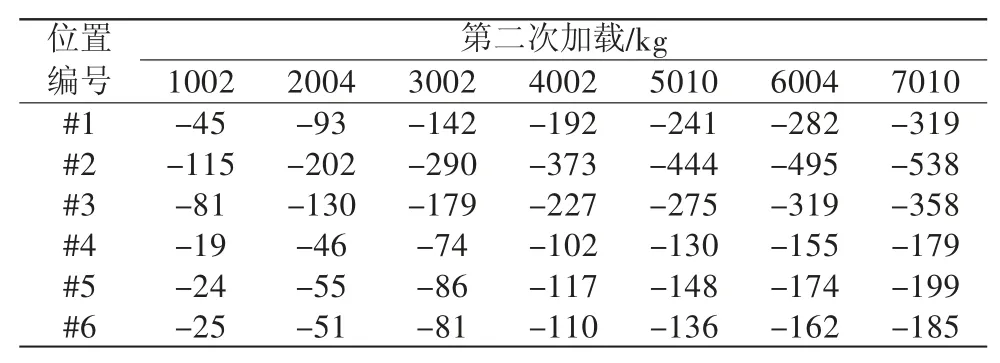
表3 行星架标定试验第二次加载应变片数据

表4 行星架标定试验第二次卸载应变片数据

每次加载与卸载的折线图如图9所示，每组应变片在单次加载与卸载过程与拉力中呈现出良好的线性关系。

然后对比各组应变片在每次加载与卸载时的线性趋势，每次加载与卸载的拟合线性关系如图10所示。

3.2 数据分析

行星架受力后产生弹性形变，行星架轴孔受到的应力与应变呈线性关系；应变片是由敏感栅构成，其工作原理是基于应变效应制作的，即导体或半导体材料在外界力的作用下产生机械形变时，其电阻值也会相应地发生变化。在理想状况下，行星架轴孔上施加的拉力应与应变片的读数呈线性关系。在统计学中，对变量进行线性回归分析，采用最小二乘法进行参数估计，R平方为回归平方和与总离差平方和的比值，表示总离差平方和中可以由回归平方和解释的比。R平方介于0～1之间，越接近1，模型越精确且回归拟合效果越好。在分析数据时，可以通过比较R平方的大小来确定拉力与应变片读数的线性度情况。

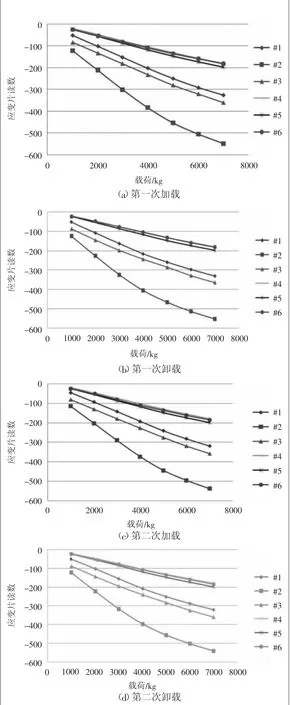
图9 行星架应变片加载与卸载数据线形图

首先分析6个位置的应变片的线性度，从图10可知，2号位置应变片的线性较差，R平方值约为0.9703～0.9842之间，1号与3号应变片的线性较好，R平方值可达到0.995左右，4号、5号、6号应变片的线性最好，平均能达到0.997以上。通过图9可以比较直观地看到，4号、5号、6号应变片在每次加载与卸载的过程中能保持较好的重叠性，3组应变片拉力与应变读数的线性关系一致性较好；1号与3号应变片虽然本身线性度较好，但是1号、2号、3号应变片的重叠性较差，3组应变片拉力与应变读数的线性关系一致性较差。

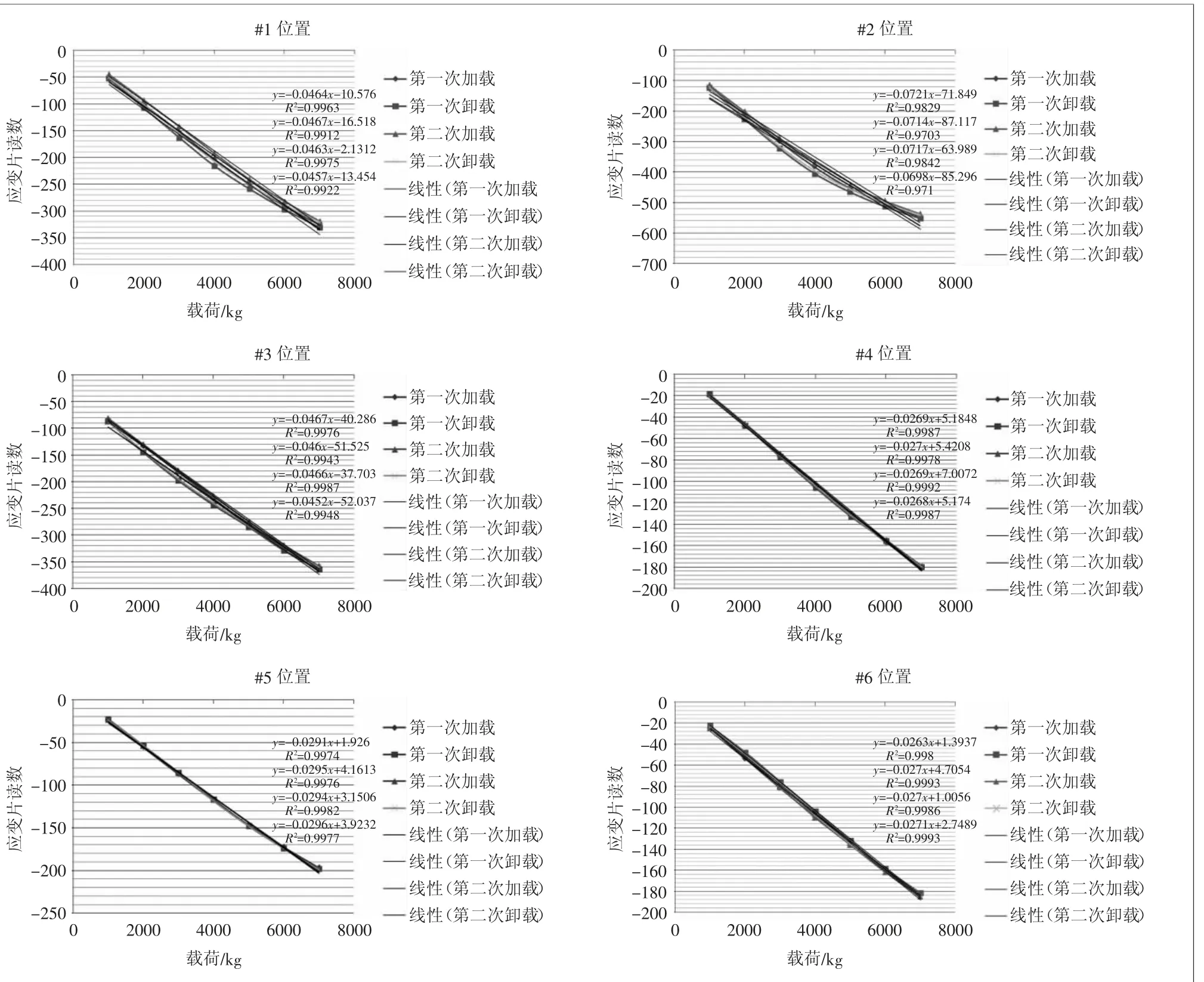
图10 各组应变片加载与卸载线性图

对比其余4组行星轮轴孔，每组轴孔的数据经过分析后得出一样的结论，4号、5号、6号应变片显示出非常好的线性度和重合度，1号、2号、3号应变片的线性度和重合度相比较4号、5号、6号应变片来说呈现出较差的趋势。

从应变片粘贴位置来看，1号、2号、3号应变片粘贴在孔1处，而4号、5号、6号应变片粘贴在孔2处，虽然两组应变片距离轴孔中心距离都为大约60 mm，但是由于孔1孔径大于孔2，导致了1号、2号、3号应变片距离受力点相对比较近，而4号、5号、6号应变片则较远。

根据圣维南原理，分布于弹性体上一小块面积（或体积）内的荷载所引起的物体中的应力，在离荷载作用区稍远的地方，基本上只同荷载的合力和合力矩有关；荷载的具体分布只影响荷载作用区附近的应力分布。1号、2号、3号应变片可能距离受力点比较近（荷载作用区），在加载和卸载的过程中，施力轴与轴孔之间的接触面积在发生变化，导致1号、2号、3号应变片区域的应力分布发生变化，3组应变片的线性与重合性较差。相比较4号、5号、6号应变片，其距离与受力点较远，应力变化只同荷载的合力与合力矩有关，所以线性和重合性较好。

4 结语

本文通过有限元分析的方法模拟行星架在系统运转过程中受到的转矩，并发现行星架轴孔沿受力方向应力比较大，随后在一个轴孔附近粘贴多组应变片，使用工装对该轴孔施加拉力，通过拉力与应变片读数的线性关系最终确定工作片和补偿片的粘贴位置。

通过对行星架5组轴孔的试验数据进行分析，6组应变片在加载与卸载过程中，拉力与应变片读数呈现出较好的线性关系。在对比每组应变片的线性关系时发现，4号、5号、6号应变片拉力与应变片读数的线性关系比较一致，而1号、2号、3号应变片线性关系一致性较差。

在分析问题原因时，发现此现象可能符合圣维南原理，1号、2号、3号应变片处在荷载作用区，受到载荷分布影响大，而4号、5号、6号应变片距离受力点较远，基本上只同荷载的合力和合力矩有关。

最终，在星型齿轮系统正式运转时，会优先考虑4号、5号、6号应变片数据进行均载特性的分析。