铅笔外观缺陷检测装置中齿轮齿条有限元分析

王铭越，王金玉，温博伦，石明顺

（安徽理工大学 机械工程学院，安徽 淮南232001）

0 引言

目前设计铅笔外观缺陷检测的自动化装置能极大地改善传统人工检测的效率，在铅笔外观检测装置中，齿条与齿条挡板通过螺钉连接，当驱动气缸推动齿条挡板时，齿条做直线运动，带动齿轮轴啮合传动，铅笔插入齿轮轴，齿轮轴转动完成待测铅笔转换待测面。齿轮齿条机构作为装置传动系统的执行机构，其结构强度直接影响检测装置的可靠性、准确性和使用寿命。为保证装置机械结构设计的合理性和可靠性，需要对系统中的关键结构部件或容易发生变形、损坏的零件进行力学分析和模态分析。采用有限元软件对齿轮齿条机构进行力学分析，主要研究齿廓面应力和变形情况，以确保齿轮齿条啮合传动机构的可靠性；对齿轮齿条进行模态分析以研究其振动特性，避免系统共振。

1 齿轮齿条结构力学分析

为实现铅笔在卡槽内的360°整周旋转，齿轮箱传动机构由齿轮轴、齿条、直线轨道、齿条挡板、支撑台、矩形钢管、压缩弹簧等部分组成。工作原理为驱动装置（气缸）推动齿条挡板，齿条带动齿轮轴转动，完成待测物转换待测面，其具体结构如图1所示。

齿轮齿条机构作为本装置传动系统的执行机构，其结构强度直接影响着检测装置的可靠性、准确性和使用寿命。为了对实际复杂工况下机构的结构强度进行有效的评估，利用SolidWorks软件建立齿轮齿条系统三维模型，导入ANSYS Workbench中进行结构动力学分析。齿轮齿条材料选择为40Cr，通过查阅材料手册查得40Cr的相关性能参数[1]，如表1所示。

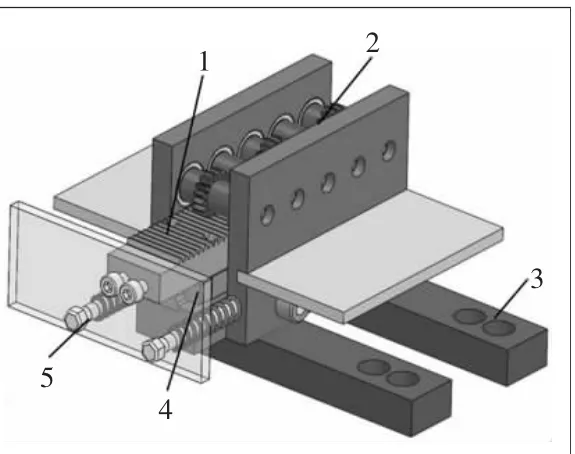
图1 齿轮箱传动装置

表1 齿轮、齿条材料属性

由于本齿轮齿条组中的各齿轮之间无相互接触，只有各个小齿轮与齿条直接发生啮合传动，进行有限元分析时，可简化为单个齿轮和齿条的配合模型。在传动过程中，当结构承受载荷逐渐变大时，接触区域会出现微小形变，导致啮合接触面逐渐扩大，齿轮齿条之间的啮合力呈指数增长。为了提高数值模拟的真实性和可靠性，减少或消除有限元计算过程中误差，在对模型进行网格划分时，可适当地减小沿齿轮轴向和齿条厚度方向的网格密度。初设啮合区域网格尺寸为0.4 mm，其它区域选用1 mm网格，划分成341 681个单元，得到583 285个节点。模拟实际工况，通过添加自由度约束，使得齿轮只能绕Z轴旋转，旋转角速度为50 rad/s；齿条通过导向机构只存在X轴方向上的平动。通过仿真分析，得到齿轮齿条在极限工况下的应力、应变及变形云图，如图2～图4所示。

由以上仿真分析结果可知：1）齿轮齿条啮合传动中的最大接触应力发生在轮齿啮合接触处，即齿廓面在节线附近的位置；2）在系统最高负载时，齿轮齿条间最大接触应力为445.89 Pa，远小于齿轮齿条材料屈服强度；极限条件下可能造成齿轮齿廓面的最大变形量为5.203×10-9mm，在允许变形范围内。

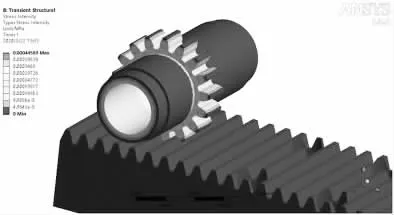
图2 齿轮齿条啮合应力云图

图3 齿轮齿条啮合应变云图

图4 齿轮齿条啮合变形云图

2 齿轮齿条振动模态分析

对齿轮齿条系统进行模态分析，首先确定齿轮齿条系统的各阶模态参数。齿轮齿条系统的模态参数主要包括系统固有频率、固有振型矢量、模态质量、模态刚度、模态阻尼等[2-4]。可将齿轮齿条系统有限元的运动方程写为

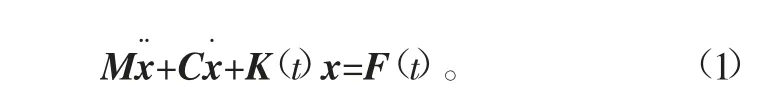
式中：M为质量矩阵；C为阻尼矩阵；K为刚度矩阵；x为位移向量；F（t）为作用力向量；t为运动行程持续时间。

对于该装置中的齿轮齿条线性振动系统，若不计阻尼的影响，则可以将其自由振动的运动微分方程的一般形式表示为

式中，X为系统内各元素点的振幅。将该方程的解表示为简谐运动形式，可得

其中，ejwt为消除因子。

根据模态分析理论，将啮合区齿轮齿廓面和齿条齿廓面定义为一个接触对，其中齿条齿廓面为目标面，齿轮齿廓面为接触面。在齿轮轴心处添加圆柱面和旋转副约束；齿条底部添加移动副和2自由度的位移约束。因为越高阶振型对系统动力特性的影响越小，所以只分析系统工作条件下可能引起共振的低阶频率即可，将本系统仿真模态数设为6，频率范围为0～108Hz，得到齿轮齿条前6阶固有振型云图，如图5～图10所示。

图5 1阶模态固有振型

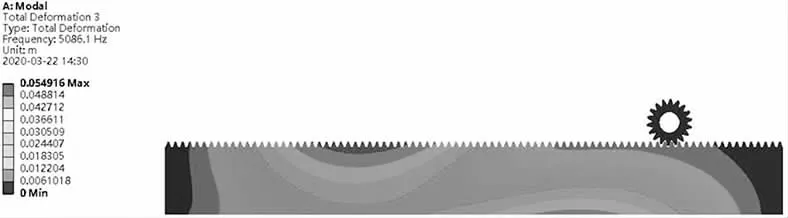
图7 3阶模态固有振型

图8 4阶模态固有振型

图9 5阶模态固有振型

图10 6阶模态固有振型

由前6阶模态固有振型分析可知，齿轮齿条组的最低模态频率为2139 Hz，当装置达到最高传动效率情况下，所选气缸型号的外部最大激励频率fmax约为203.67 Hz，此时外部激励频率并不在系统固有频率的影响范围之内，由此可以确定该驱动系统可以成功地避开共振频率，系统不会发生共振。

3 结语

利用有限元软件对齿轮齿条进行了力学分析，确保了结构强度满足相关使用要求。利用模态分析确定了齿轮齿条系统前6阶模态固有振型，得出系统最高运动效率条件下，外部激励频率也小于齿轮齿条机构固有频率，由此可知，以不同的检测效率运行时，系统均不会引起共振。