细绳牵引条件下二体弹性碰撞的分析与讨论
张 孟 陆 慧 吴赵龙 钟菊花
(1 华东理工大学物理系,上海,200237)
碰撞是物质间作用的常见形式,表现为两粒子或物体间极短时间的相互作用,碰撞过程中伴随着动量、能量和角动量的转化和转移。因其涉及物理学中诸多的守恒定律,故碰撞知识点是高中和大学物理的重要内容。现有的物理学教材和文献对两小球的非牵引碰撞做了非常详尽的讨论[1-7],但对于细绳牵引条件下的碰撞却鲜有文献报道。文献[3]以高中物理教学常用的速度关联方法对理想刚性细绳绷直条件下的两球碰撞问题展开了多种解法的讨论,而文献[4]从能量角度定性讨论了牵引碰撞问题,但对牵引过程的动力学方程和两物体运动状态随时间的演化过程没有给出具体的定量分析。为深入研究牵引碰撞的本质规律,本文对两小球更为一般的弹性牵引碰撞进行分析与讨论,细绳牵引下碰撞过程模型如下:
如图1所示,光滑平面上用长为x0的轻质细绳连接质量分别为m1与m2的小球,初始时细绳松弛,m1速度大小为v0,m2静止,细绳拉紧以后,两小球运动状态的变化类似碰撞过程,故称为牵引碰撞。
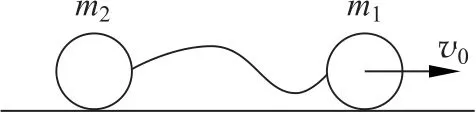
图1 牵引碰撞示意图
当小球和细绳均完全无弹性时,两小球发生完全非弹性牵引碰撞,碰撞后两小球以相同速度继续运动[4]。然而,一般情况下小球和细绳均具有一定弹性,以下将建立谐振子模型对弹性牵引碰撞的性质进行研究。
1 模型建立
为了描述牵引碰撞过程中小球和细绳的弹性形变,首先建立简谐振子模型代替系统中的弹性部分。该模型清晰直观,简化了弹性牵引碰撞的具体过程,尽管忽略了细绳的松弛状态,但仍可以将牵引碰撞的性质阐述清楚。
如图2所示,该谐振子模型将两小球发生弹性牵引碰撞时未形变的部分看成质量分别为m1与m2的刚性物体,而形变部分质量很小,可看作轻质弹簧(原长为x0),并假设回复力F与形变位移x-x0成正比,又因为碰撞过程通常存在能量耗散,设耗散力f与形变速度˙x成正比[2],即

图2 弹性牵引碰撞的谐振子模型
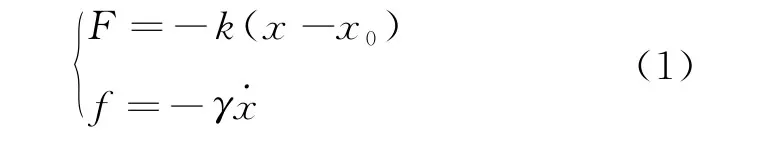
特别地,若两小球发生完全弹性牵引碰撞,则弹簧振子形变过程中不存在能量的耗散,即γ=0,耗散力为零。除此之外,在非完全弹性牵引碰撞中,γ均不为零,且γ越大表示牵引碰撞中能量耗散越快。阻尼存在时弹性牵引碰撞的阻尼力如图3所示。
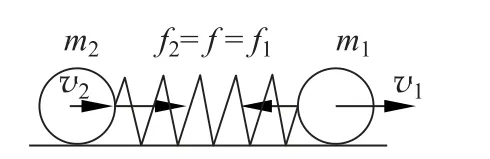
图3 阻尼存在时弹性牵引碰撞的示意图
为方便分析,进一步假设该模型的初始状态为:物体m1以v0速度运动,m2静止,且弹簧处于原长x0。以下在该模型的基础上对完全弹性牵引碰撞与非完全弹性牵引碰撞进行分析讨论,且考虑到最终要分析实验室系中的观察结果,故为避免参照系变换引入的麻烦,以下分析直接在实验室系进行计算。
2 完全弹性牵引碰撞
对于两小球的完全弹性牵引碰撞,设x1与x2分别为物体m1与m2的位置,则根据动量守恒定理与动力学方程,有
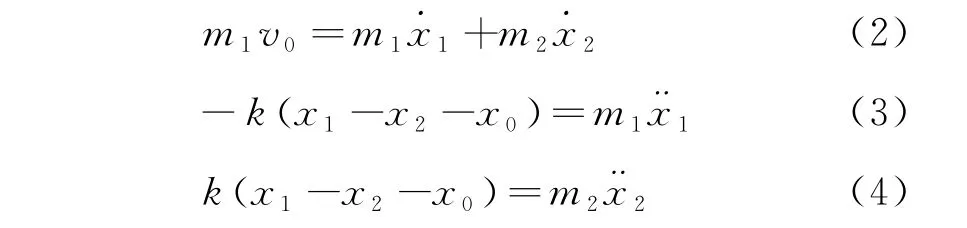
分别对式(3)与式(4)求导,并与式(2)联立,可得
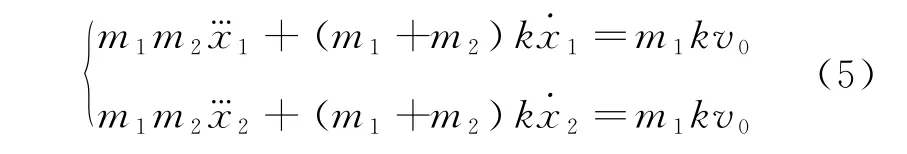
为求解式(5)的三阶常系数非齐次微分方程,列出其初始条件
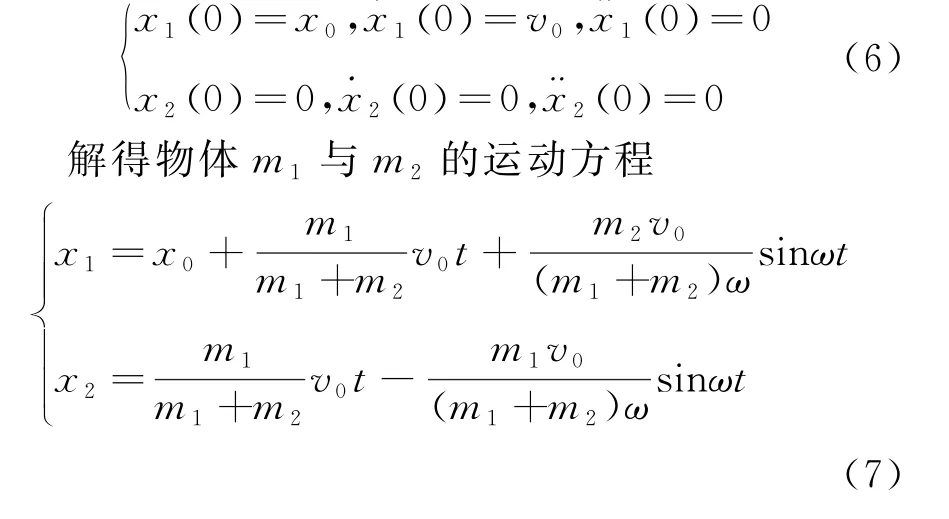
进一步计算可以得到两物体的速度大小v1与v2以及弹簧长度x随时间的变化关系
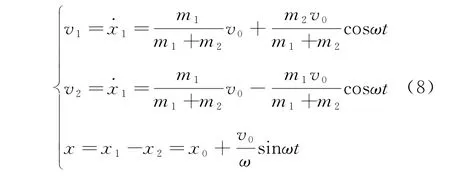
采用MATLAB对上述解析式进行数值计算和分析,给出两小球的速度v随时间t演化的曲线图,其中m1=1.5kg,m2=1kg,x0=1m,v0=1m/s,k=0.6N/m。
分析式(8)并对照图4可知,在完全弹性牵引碰撞中,两小球的速度随时间发生周期性变化,且谐振子的振动永不停止。速度表达式中的常数项等于质心速度,振荡项符号相反,即动量在两小球之间不断地发生周期性交换;做伽利略变换后,质心系中两物体反相位振动,因而弹簧长度以相同频率周期变化,即能量在动能与弹性势能之间不断转化。同时,系统的总动量守恒,总动能在谐振子恢复原长时守恒,满足完全弹性牵引碰撞的要求。
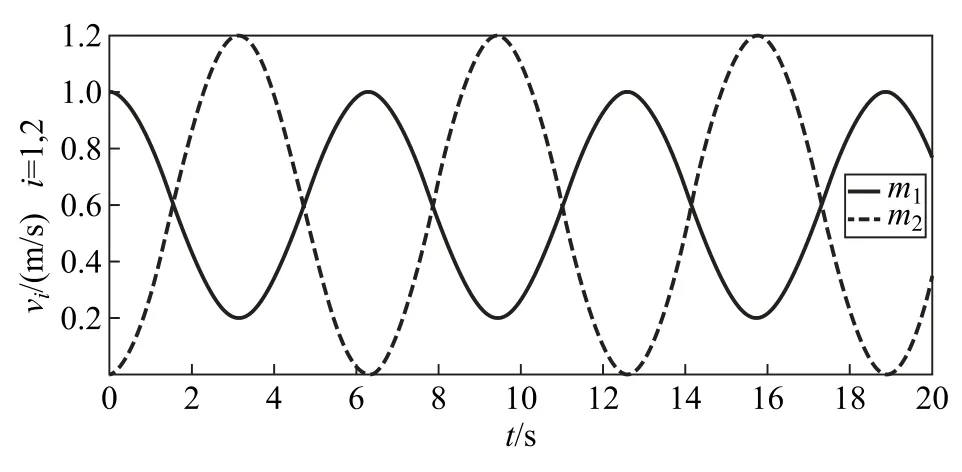
图4 完全弹性牵引碰撞后两物体的v-t图
特别地,当小球和细绳完全失去弹性时,即k→∞,ω→∞,则运动方程化为
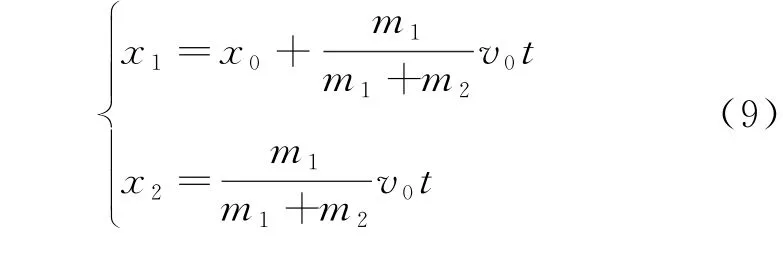
即两小球以相同速度继续运动,类似完全非弹性牵引碰撞。
3 非完全弹性牵引碰撞
对于非完全弹性牵引碰撞,γ≠0,则动力学方程式(3)与式(4)应修正为
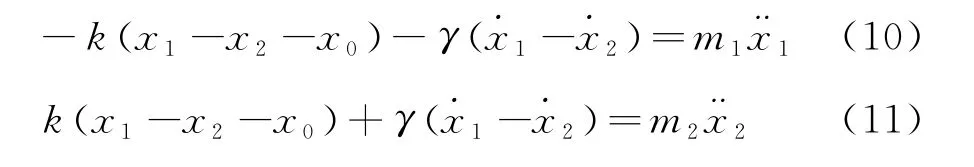
对式(2)求导可得
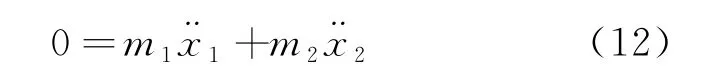
分别对式(10)与式(11)求导,并与式(2)、式(12)联立,可得三阶常系数非齐次微分方程
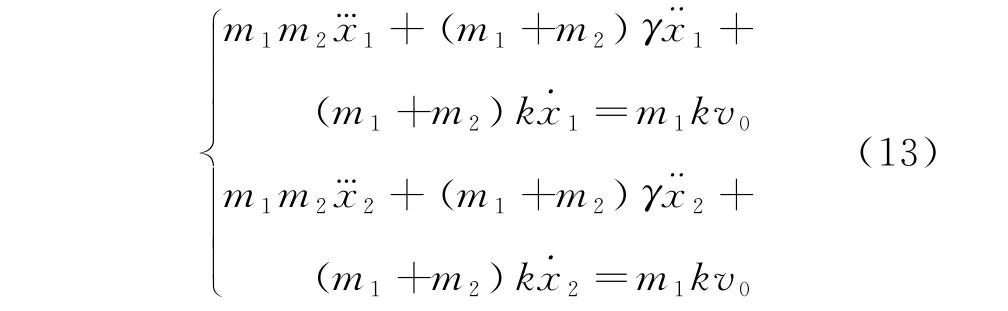
同时,初始条件修正为
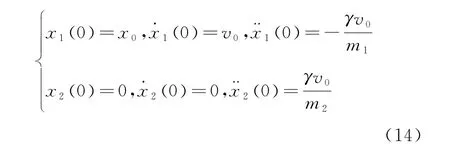

进一步计算可得

②β=ω时,解得
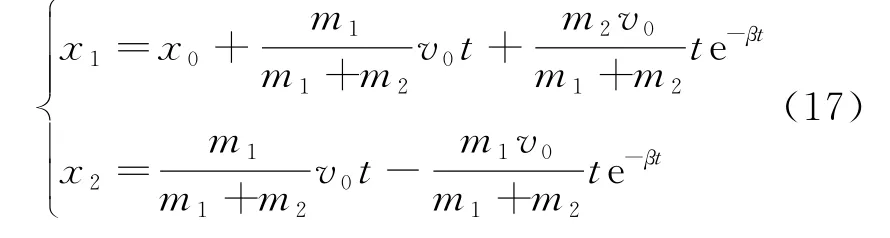
进一步计算可得

进一步计算可得

分析式(20)可知,当形变过程耗散较慢时,两物体相对速度大小与弹簧长度衰减振荡,经过更长时间后振荡项才衰减为零,最终两物体仍以相同速度运动,弹簧恢复原长。
图5和图6分别给出了非完全弹性牵引碰撞(β>ω,β=ω和β<ω)时两物体m1和m2的运动状态v-t图。其中m1=1.5kg,m2=1kg,x0=1m,v0=1m/s,k=0.096N/m,γ分别为:0.83N·s/m(β>ω),0.48N ·s/m (β=ω),0.13N·s/m(β<ω)。

图5 非完全弹性牵引碰撞后物体m1的v1-t图
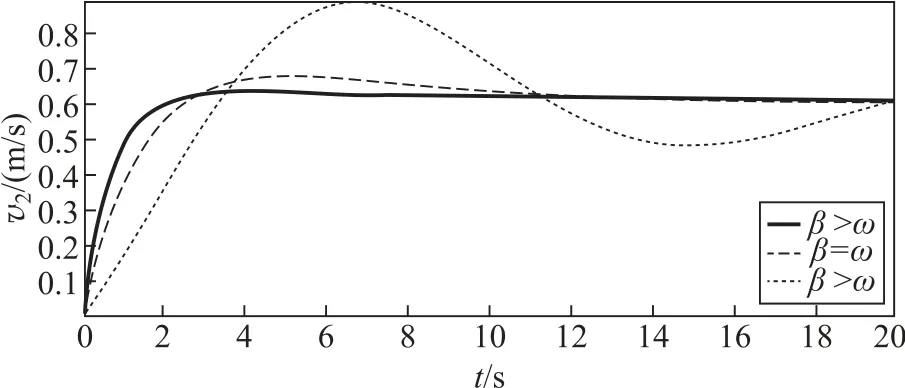
图6 非完全弹性牵引碰撞后物体m2的v2-t图
将图5和图6与式(16)、式(18)、式(20)对照可知,当形变过程耗散较快时,两物体相对速度大小与弹簧长度单调衰减,且β>ω时较β=ω的情况衰减得更快;当形变过程耗散较慢时(β<ω),两物体相对速度大小与弹簧长度振荡衰减。经过长时间后两物体均以相同速度运动,弹簧长度也均恢复原长。
需要指出的是,由于细绳只有伸长时才会有收缩张力,压缩时细绳变软,不会有拉伸的张力,所以严格地说,本文采取的弹簧振子模型,与细绳模型还是存在差异的。但从上面讨论的结果来看,细绳模型在完全弹性牵引碰撞时两小球也做能量不损耗的周期运动,只是每个周期内前半段与后半段运动不对称,一段受到回复力,另一段细绳变软不受力,两小球会发生碰撞,作用效果类似向外的回复力;非完全弹性牵引碰撞时,阻尼力仅在细绳拉伸时存在,压缩时同样不受力,运动形式也与弹簧振子模型非常相似。因此,在弹簧振子模型基础上,本文对细绳牵引条件下两体碰撞做了有益的讨论和研究。
此外,如果在质心系中考虑该问题,可以将二体问题转化为单体问题。以质心为原点,两小球的位置分别为与,以完全弹性情况为例,物体m1在质心系中的折合质量为,列出其相对于物体m2的动力学方程
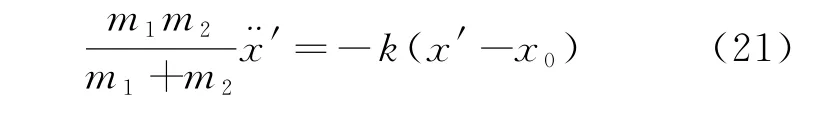
由此可以解得相对位移与相对速度

两质点相对质心系的速度为
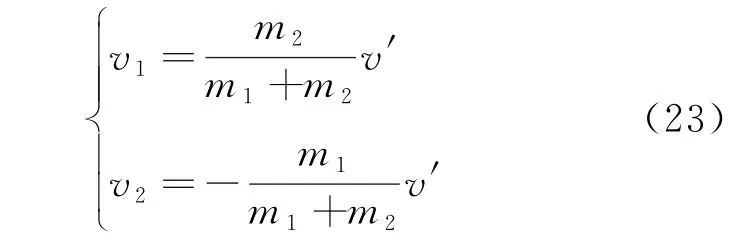
因为最终需要求解实验室系中两小球的运动,故需要根据以下方程组进行变换
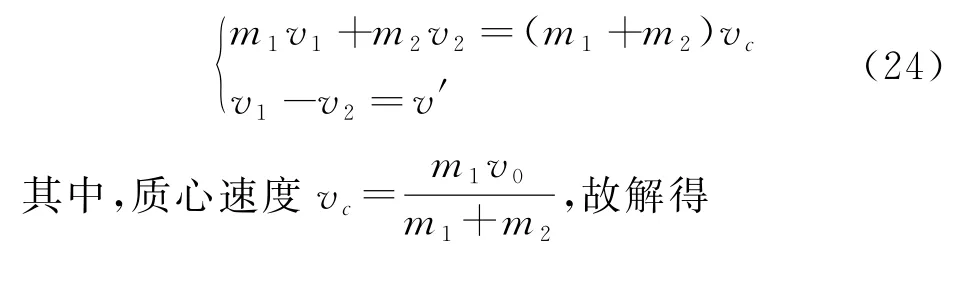
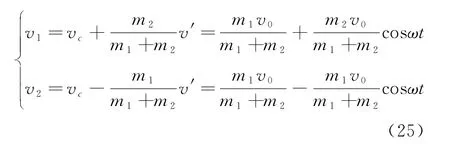
该结果与上文中在实验室系的结论式(8)相一致。因此,如果读者对折合质量与参照系变换较熟悉,则在质心系中计算可以相应减少数学运算的复杂度。
4 结语
通过对牵引碰撞采用谐振子模型的分析与讨论,可以得到弹性牵引碰撞的具体动力学表达式和各种性质:
①两小球发生完全弹性牵引碰撞后,总动量与总能量均不损失,且谐振子恢复原长时动能守恒。式(8)与式(9)表明,两小球的相对速度与谐振子长度发生周期性变化,永不停止。
②两小球发生非完全弹性牵引碰撞后,总动量不损失,但总能量减小。式(16)、式(18)与式(20)表明,当耗散力较大时,两小球相对速度与谐振子长度不断衰减,当耗散力较小时,两小球相对速度与谐振子长度衰减振荡,且最终均趋于相同的运动状态:两小球以相同速度运动,弹簧恢复原长。
一般情况下,碰撞总伴随能量损失,因而非完全弹性牵引碰撞更符合实际情况。与完全非弹性牵引碰撞类似,非完全弹性牵引碰撞后两小球以非线性变化方式也趋于以相同速度运动,故文献[1]~文献[4]中相关的习题解答是合理的。

