量子力学的基本对易关系

黄永义

(西安交通大学理学院,陕西 西安 710049)

量子力学的基本对易关系是位置和其共轭动量的对易关系[x,p x]=iħ,该对易关系包含了量子力学最核心的规律,是量子力学和经典力学最根本的区别。和其他物理理论类似,基本对易关系也有一个发展过程,这个发展过程也是矩阵力学的发展过程。这个发展过程是非常快速的,自克喇默斯色散理论在1924年提出以来,基本对易关系的三种形式,库恩-托马斯求和规则的萌芽形式,海森堡量子化条件的过渡形式和玻恩-约当、狄拉克的现代形式都发生在1925 年。本文先简要介绍克喇默斯色散理论,然后介绍库恩-托马斯求和规则,海森堡量子化条件和玻恩-约当的贡献、狄拉克量子泊松括号。本文的最后简要地介绍了矩阵力学求解氢原子的过程,较详细地阐述了波动力学与矩阵力学的等价性。

1 克喇默斯色散理论

康普顿效应的实验使得人们不得不承认爱因斯坦光量子理论的正确,但这就势必要推翻现有的电磁理论体系,而麦克斯韦电磁理论看上去又是如此牢不可破,无法动摇。1924 年玻尔、克喇默斯、斯莱特发表了玻尔-克喇默斯-斯莱特(BKS)理论试图解决光波的连续性和原子跃迁的不连续这个两难问题[1]。在BKS理论看来,当一个原子在定态时,它会通过辐射场和别的原子建立联系。这个虚辐射场来自于具有可能原子跃迁频率的虚振子,它具有诱发原子跃迁的功能。由于玻尔对光量子的消极态度,BKS理论不是调和光的波动和粒子的矛盾,而是想把连续的电磁场和不连续的原子跃迁联系起来。虚辐射场作用是通过确定原子的跃迁几率得到统计的能量、动量守恒,这意味着要放弃原子对辐射发射和吸收的因果描述。由此BKS得到结论:能量、动量守恒只在统计意义上成立,而在基元过程不是严格成立。能量、动量不守恒代价太大,遭到了爱因斯坦、泡利等人的强烈反对。1925年博特和康普顿等人独立地从实验上否定了BKS理论,证实光子和电子相互作用的基元过程能量和动量守恒也精确成立[2,3]。他们对康普顿效应实验进行细致研究,实验结果显示康普顿散射中反冲电子和散射光子存在明显的同时性和角度关联,这和BKS理论完全矛盾,因为后者预言散射光的发射在时间和方向上都是随机的,与反冲电子之间不存在显著的同时性和角度相关性。

虽然BKS理论被否定,但它的一些思想也不是毫无意义,克喇默斯利用虚拟振子的思想研究了色散现象并取得了积极的结果。为此我们先介绍一下经典的色散理论,一个原子和一个价电子被视为一个电偶极振子,一束偏振的单色光E=E0cos(2πνt)照射该原子时,会产生和光偏振方向相同的电偶极矩p=-ex,由牛顿第二定律可得电偶极矩满足的方程

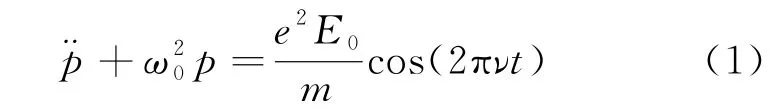
式中m为电子质量,=k/m振子的本征频率。式(1)稳态解为

如果原子有k种极化,每种极化有f k个电子,则原子的极化强度为

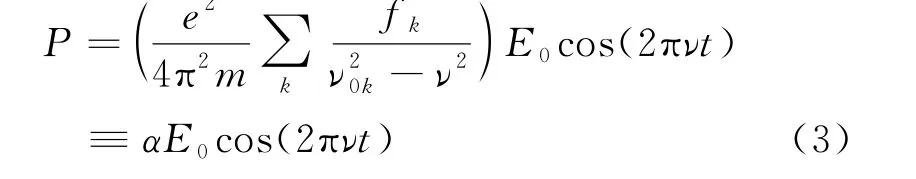
由此可得

式(4)的介电常数α和原子对光的折射率联系在一起,因此称原子对光的响应为色散理论。

以上是原子对光色散的经典结果,1921年拉登堡将经典的色散理论的强度因子f和爱因斯坦自发辐射系数A联系在一起,得到,其中νki=（E k-E i）/h,h为普朗克常数。将经典形式的式(3)改写为量子形式[4]

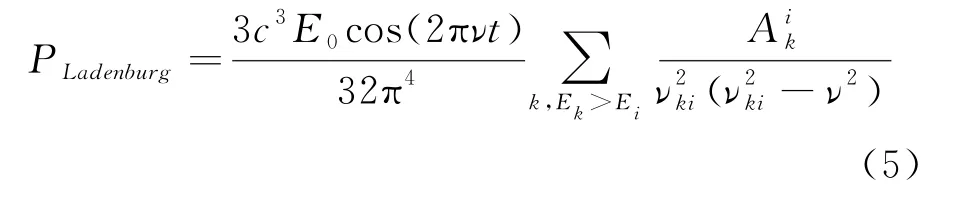
式(5)中的i表示原子的基态,k表示激发态。这种形式的色散体现了原子对光的吸收,原子吸收光,同时原子的能级由基态i向高能级k跃迁。1924年克喇默斯将i推广为激发态,将拉登堡色散公式(5)改写为

其中νik′=（E i-E k′）/h[5]。式(6)第一项内涵和同式(5)相同,第二项对低于i能级的k′能级求和。第二项表示原子吸收光,同时原子的能级由高能级i向低能级k′跃迁,这种负吸收对应于爱因斯坦的受激辐射。反常色散的第二项后来被拉登堡等人的一系列实验证实。1924年克喇默斯,玻恩和范夫莱克独立地借助于玻尔对应原理推出了克喇默斯的色散公式(6)[6,7,8]。

2 基本对易关系的萌芽形式:库恩-托马斯求和规则

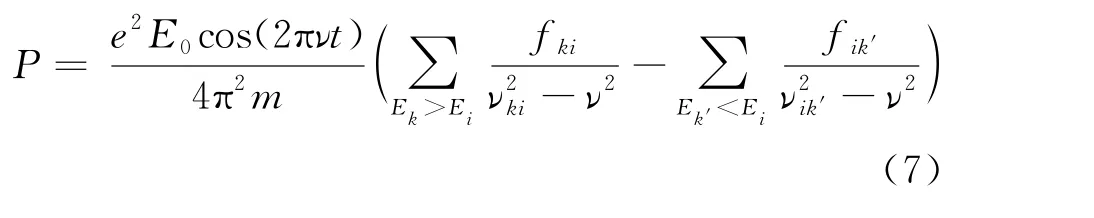
此式为库恩-托马斯求和规则[9,10]。库恩和托马斯没有给出进一步研究结果,只需要稍微前进一点点,他们就能得到基本对易关系的过渡形式:海森堡量子化条件,因此库恩-托马斯求和规则只能算基本对易关系的萌芽形式。事实上由玻尔对应原理,可得爱因斯坦自发辐射系数和x ki的关系式[11],

后文还会出现玻尔的对应原理,这里我们对对应原理作较详细的说明。对应原理是旧量子论时期玻尔的一个重要贡献。在矩阵力学出现后玻尔曾表示量子力学的整个工具,可以看成是对包含在对应原理中的那些倾向的一种精确表述。玻恩也认为,对应原理是从经典力学通向量子力学的桥梁。什么是对应原理呢? 1918 年玻尔是这样表述的:没有关于定态间跃迁机制的详细理论,我们当然不能普遍地得到两个这种定态之间自发跃迁几率的严格确定法,除非各个n是一些大数……对于并不是很大的那些n值,在一个给定跃迁的几率和两个定态中粒子位移表示式中的傅立叶系数值之间也必定存在一种密切的联系[12]。

从玻尔的论述来看对应原理主要目的是试图找到影响跃迁几率的相关因素,而玻尔表述的跃迁几率和粒(电)子位移表示式的傅里叶系数值之间存在着密切的联系展现了玻尔的强大的物理直觉,后来量子力学证实了跃迁几率和经典傅里叶系数对应的跃迁振幅有关。玻尔所说的跃迁几率与经典振幅之间的密切的联系包含了一些重要的定性对应,比如可以通过对经典振幅的分析确定量子跃迁为零的情形。这样他就可以导出量子跃迁的选择定则,以及跃迁辐射的偏振性质,而这些在旧量子论时期具有极大的重要性。玻尔对应原理的表述中“除非各个n是一些大数”这句话为人们提供了对应原理的具体使用方法,实际情况对应原理通常是这样使用的,对于从定态n′～n的跃迁:

a.当n′与n都是大数,且都比n′-n大得多时,跃迁辐射的频率与相应轨道的经典绕转频率的某个倍频 (或者说与一个经典泛频) 基本重合。特别是,当n′与n为相邻定态时,跃迁辐射的频率基本等于相应轨道的经典绕转频率。

b.在上述大量子数极限情形下,跃迁几率正比于相应泛频所对应的经典振幅的平方。

c.上述规律不仅在大量子数极限下成立,而且或许在任意量子数下也成立,这个情况具有很大猜测性。

3 基本对易关系的过渡形式:海森堡量子化条件

1925年克喇默斯和海森堡采用了玻恩的做法,即把对作用量J的微商改写为差分后导出了完全量子化的克喇默斯-海森堡色散公式[13]

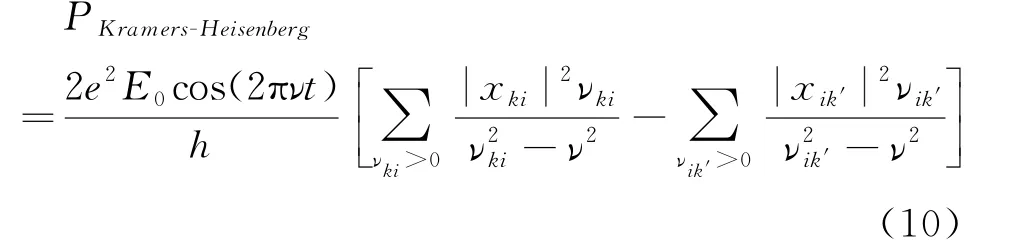
式(10)中量子物理量x ki和其模平方|x ki|2的物理意义如前所述。为了计算色散公式(10)中|x ki|2,必须弄清楚位置坐标x傅里叶分量xτ对应的这个量子物理量x ki的物理本质到底是什么,遵循的运动方程,x ki的具体形式和两个量x ki之间的运算规则,特别是乘法规则。玻恩,海森堡,约当讨论后认为物理量x ki的乘法不同于一般物理量的乘法,而应该遵守未知的某种符号乘法规则,那种神秘的符号乘法规则到底是什么呢? 这些问题都是当时量子理论急需要解决的,对当时量子理论的发展具有极大的重要性。1925 年海森堡天才地把位置坐标改写成矩阵,其矩阵元为x kiei2πνki t。这样,物理量x ki的物理本质就是位置坐标的矩阵元(除去时间相关的相位因子ei2πνki t),两个物理量x ki的符号乘法即简单的矩阵相乘。海森堡解决了上述问题,很快创立了矩阵力学[14,15]。

玻尔的氢原子理论中一系列定态对应于一个能量E(n),E(l)等,两个能级直接的跃迁原子会放出一个光子,光子的频率满足玻尔的频率条件

式中ħ为约化普朗克常数。显然就频率而论,满足里兹组合定则,即

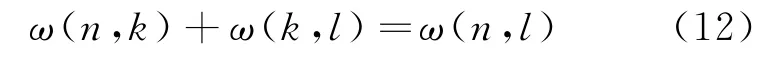
经典方法用振幅和频率描述运动,必须把位置坐标写成傅里叶级数

式中τ在无穷范围内取整数,ω(n)是基频,τω(n)为谐频。x(t)是实数,使得关系式x-τ=xτ*成立。量子论中海森堡用位置坐标矩阵代替式(13)来表达原子的信息,位置坐标矩阵元为

式(14)中l=n-τ为式(13)中的各项对应,并且假定x(l,n)=x(n,l)*和ω(l,n)=-ω(n,l)成立。这样一种替换是思维的质的飞跃,它将矩阵引入了量子力学,下面的分析会看到（x(n,l)）就是一个无限维方矩阵。

海森堡将式(15)转译至式(16)的形式不是没有理由的,主要的原因是使其理论满足里兹组合定则式(12)的要求。事实上,量子论中的光是原子中电子在初末状态跃迁的结果,经典情况下频率关系为τω(n)+(β-τ)ω(n)=βω(n),按照里兹组合定则要求,与经典频率关系对应的量子论中频率关系为ω(n,n-τ)+ω(n-τ,n-β)=ω(n,n-β),按此脚标的对应关系,式(15)必然转录成式(16)的形式。由式(16)知,位置坐标的平方x(t)2也是一个矩阵,其矩阵元为B(n,n-β)eiω(n,n-β)t。如果是不同的两个物理量x(t)=∑xτeiτωt,y(t)=∑yρeiρωt的乘积,经典的形式为z(t)=∑τzτeiτωt=,式中

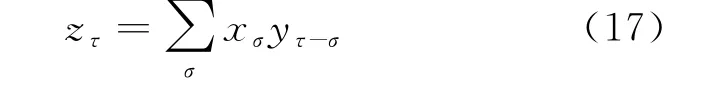
式(17)转译至量子论为

量子论中两个物理量乘积的表达式(18)实质上就是数学上两个矩阵的乘积。

有了量子论中物理量是矩阵的崭新的思想,现在考查一下玻尔-索末菲量子化条件

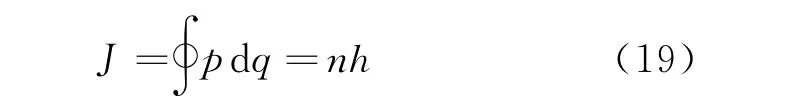
具有的新形式了。为此我们还是从经典表达式(13)出发,借助玻尔对应原理将量子化条件转译至量子论的表述。由式(13)得量子论条件表述为

现在需要将式(21)通过玻尔对应原理转译至量子论中。玻尔对应原理的要求:当主量子数n很大时量子频率过渡到经典的频率,即→ω(n,n-τ)。参照玻尔的频率条件式(11)可得

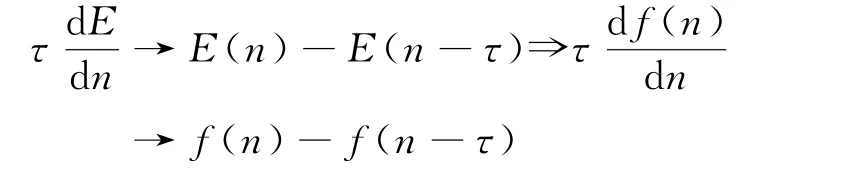
上式中f(n)为任意函数,即玻尔对应原理要求将经典情况函数f对量子数n微商替换为量子论情况下差分的形式。海森堡从玻恩那里学到了将式(21)转译为满足克喇默斯的色散公式或库恩-托马斯求和规则的差分形式

式(22)为海森堡量子化条件。

4 基本对易关系的现代形式:玻恩和约当的贡献

海森堡发表了他的新力学后,玻恩和约当进一步发展了海森堡的思想,他们做出的最重要的工作是将海森堡量子化条件式(22)改写为一个更简洁的形式[16]。玻尔-索末菲量子化条件式(19)可写为

物理量p,q在量子论中都是矩阵,式(25)表示pq-qp矩阵为对角矩阵,其对角元（pq-qp）nn为-iħ。式(25)可以写成简洁的形式如下

5 基本对易关系的现代形式:狄拉克量子泊松括号

1925年9月狄拉克的导师R.否勒收到海森堡基于对应原理的仅使用物理上可观察量建立矩阵力学的文章(一人文章),否勒建议狄拉克仔细研读这篇文章。狄拉克的注意力被海森堡文章中神秘的令人费解的数学关系所吸引,几个星期后狄拉克回到剑桥大学,突然意识到海森堡文章中的数学形式和经典力学中粒子运动的泊松括号一样具有相同的结构。从这个想法出发,狄拉克很快地发展了基于非对易动力学变量的量子理论-量子泊松括号,我们看看狄拉克关于量子泊松括号的工作[17]。

两个量子物理量的乘积如何过渡到它们的经典泊松括号呢? 按海森堡的观点,量子力学中任意力学量x和y都应该具有矩阵形式,两个力学量的乘积不满足交换律,即xy≠yx。为了方便使用对应原理,假设x矩阵的矩阵元x(n,n-α)的量子数n是大数,α是比n小得多的数。这样可以将x的矩阵元简写为x(n,n-α)=xαk,J r=n rh,h为普朗克常数,角标r代表系统的一对共轭变量:作用量变量J和角度变量w=ωt/2π的自由度。令m=n-α-β,这个量xy-y x的矩阵元（xy-y x）nm的经典对应为

式(28)中α,β均为小量子数,n,m是表示初末态大量子数,α+β=n-m为约束条件,第一个求和号代表对初末态之间的各种可能的跃迁求和,第二个求和号表示对共轭量J r和w r的自由度求和。xy-y x整体的矩阵对应于-,而式(28)中初末态之间的各种可能的跃迁求和已包含在矩阵乘法里面。进一步我们得到

式中p r和q r是系统的任意一对共轭量。由于经典泊松括号在正则变换下保持不变,因此式(29)成立,即在大量子数情况下量子力学中的xy-y x矩阵对应于iħ乘以经典泊松括号{x,y},狄拉克依据玻尔对应原理进一步假设任何量子数情况下两者也相等即

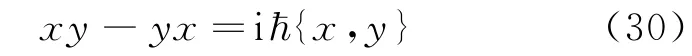
由位置和动量的经典泊松括号{q i,p j}=δij,狄拉克得到了玻恩和约当曾得到的量子力学的基本对易关系[q i,p j]≡q ip j-p jq i=iħ{q i,p j}=iħδij。

海森堡,玻恩,约当三人完成了矩阵力学的完整表述[18],给出了算符的海森堡运动方程,由此建立了完整的矩阵力学。事实上,设f为位置q和动量p的所有有理函数,由基本对易关系式(26)得到

令f等于系统哈密顿量H,哈密顿正则方程=,则式(31)变为

这样所有是p,q的有理函数O(p,q)的运动方程为

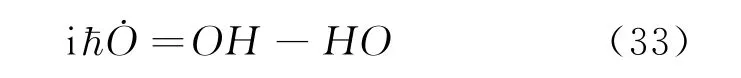
此式为算符O的海森堡运动方程。

6 利用矩阵力学求解氢原子

用现代的术语来说矩阵力学是海森堡绘景下能量表象的量子力学,算符的海森堡的运动方程式(33)是矩阵力学的核心方程,算符在能量表象下就是矩阵,算符的海森堡运动方程也是一个矩阵方程。矩阵力学处理量子力学问题,一般通过正则变换将系统的哈密顿量对角化,即W=SHS-1,式中S为变换矩阵,W为对角化的哈密顿量,其对角的矩阵元就是系统的能量本征值。任意算符也需要相应的正则变换,即¯O=SOS-1,变换后海森堡运动方程为

将式(34)两边取(nm)矩阵元,考虑到W为对角化矩阵W ni=W niδni=W nnδni得

式(35)的解为

算符O的矩阵随时间的变化关系为

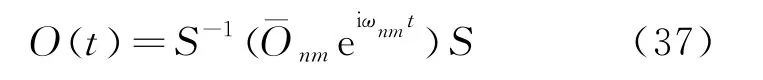
可见在矩阵力学里力学量矩阵随时间的变化关系比较简单。具体的物理问题往往和力学量矩阵元的模平方成正比,如光谱的强度和原子的位置矩阵元的模平方|r nm|2成正比,力学量矩阵随时间的变化并不显得那么重要,而矩阵力学的主要任务是通过正则变换将系统的哈密顿量对角化获得系统的能量本征值。如何通过变换将系统的哈密顿量对角化呢? 一般先找到系统相互对易的力学量完全集,取这些力学量为共同表象,则这些力学量同时具有确定的值,然后根据由基本对易关系导出的力学量之间的对易关系和某力学量矩阵元的模平方恒大于等于零可得这些力学量的量子化的本征值。利用矩阵力学可以求得（j2,j z）表象下角动量平方j2和角动量在z方向分量jz的本征值,式中j=。

需要说明的是,矩阵力学通过正则变换求得系统的能量或力学量的本征值,需要很高的技巧寻找和构建合适的物理量,需要计算繁杂的对易关系,能精确可解的系统是十分有限的,如一维谐振子、角动量和氢原子是精确可解的系统。事实上波动力学精确可解的系统也是很少的。比较重要的是对系统哈密顿量进行正则变换W=SHS-1,除了能直接得到可解系统的能量本征值,还可以对受扰动的系统进行微扰计算,如非简并微扰、简并微扰甚至含时微扰,这样矩阵力学能够解决量子力学的大部分问题。由于注重力学量的对角化,矩阵力学难以解决涉及时间演化的问题,如散射。波动力学却能很方便地处理散射问题,在处理具体问题时波动力学往往比矩阵力学简单得多,这也是波动力学能超越矩阵力学更容易被人们接受的主要原因。

7 波动力学与矩阵力学的等价性

1926年薛定谔、泡利、艾卡特各自独立证明了波动力学和矩阵力学的等价性,我们采用薛定谔的思路从以下几个方面证实两种力学的等价性[22]。

上式即是矩阵力学的基本对易关系,证明的过程中我们使用了位置、动量算符的厄米性和基矢的完备性关系。

还可以用波动力学证明矩阵力学中力学量矩阵的海森堡运动方程=oW-Wo,式中o为力学量在能量表象下的矩阵,W为对角化的哈密顿量。为此在坐标空间取正交完备归一的基矢u1(q),u2(q),u3(q),…为能量本征函数,则有

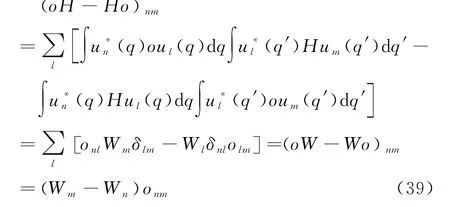
又矩阵力学的基本假设o nm（t）=o nmeiωnmt,式中跃迁频率满足玻尔频率条件ħωnm=W n-W m,由此可得

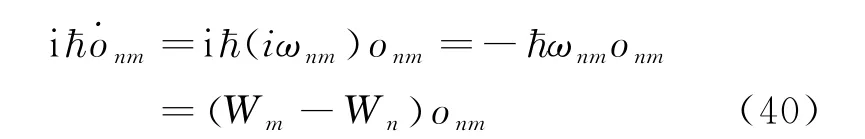
由式(39)和式(40)我们得到了力学量矩阵元的海森堡运动方程=oW-Wo（）nm,进而得到力学量矩阵的海森堡运动方程iħ˙o=oW-Wo。从上述论证看薛定谔波动力学和海森堡、玻恩、约当矩阵力学确实是等价的。

8 结语

对比波动力学爱因斯坦-德布罗意-薛定谔这条过程清晰而简单的发展线路,矩阵力学的发展则十分繁杂和曲折离奇,其中也到处闪烁着天才们的灵感和智慧,因此顺畅地整理矩阵力学的发展过程是十分必要的,这就是本文的主要工作之一。本文以量子力学的基本对易关系为抓手介绍了矩阵力学的产生背景和海森堡、狄拉克创立量子力学的灵感和工作,比较详细地阐述了基本对易关系发展的三种形式:库恩-托马斯求和规则的萌芽形式,海森堡量子化条件的过渡形式和玻恩-约当、狄拉克的现代形式。为了深入地理解量子力学,包括矩阵力学处理问题的方法,和波动力学与矩阵力学的内在联系,本文还简要地介绍了矩阵力学求解氢原子的过程,较详细地阐述了波动力学与矩阵力学的等价性。玻尔氢原子理论未能给出光谱的强度、线宽、偏振等信息,玻尔让他的学生克喇默斯研究这个问题。计算光谱的强度要用到爱因斯坦自发辐射系数,拉登堡研究色散现象时找到色散强度因子和爱因斯坦自发辐射系数的关系,拉登堡的工作是一个关键的进展,第一次把经典的色散现象和量子的能级跃迁联系起来。克喇默斯推广了拉登堡的色散结果,成功地建立了克喇默斯色散理论。库恩和托马斯由对应原理将克喇默斯色散公式过渡到经典的JJ汤姆逊色散公式,得到了库恩-托马斯求和规则,如文中所述,这个求和规则是基本对易关系的萌芽。海森堡和克喇默斯合作,得到了完全量子化的克喇默斯-海森堡色散公式,该公式中出现了与位置坐标傅里叶分量xτ对应的量子物理量x ki,海森堡研究清楚了物理量x ki的物理本质就是位置坐标的矩阵元,由此建立基本对易关系的过渡形式:海森堡量子化条件。海森堡量子化条件虽然不是基本对易关系的现代形式,但却是矩阵力学的开端,是量子力学概念的突破,因为海森堡明确将矩阵引入量子力学。我们也看到原子对光色散理论的研究直接导致了矩阵力学的诞生。玻恩和约当完全沿着海森堡的道路,得到了量子力学基本对易关系的现代形式。狄拉克受到海森堡矩阵力学文章的启发另辟蹊径,由矩阵乘法的不对易想到经典泊松括号,建立了量子泊松括号和经典泊松括号的对应关系,由此轻而易举地得到了基本对易关系。有了基本对易关系,建立整个矩阵力学体系便是顺理成章的事了。