基于传递矩阵算法的裂隙注浆扩散机制研究
刘若坤 ,王 伟,黎海滨,刘佳佳,姚 泽
(1.石家庄铁道大学 国防交通研究所, 河北 石家庄 050043;2.石家庄铁道大学 土木工程学院, 河北 石家庄 050043;3.石家庄铁道大学 交通运输学院, 河北 石家庄 050043)
在裂隙岩体注浆工程中,为保证注浆效果需要根据围岩裂隙条件及浆液特性合理确定注浆参数。关键的注浆参数主要包括扩散距离、水灰比、注浆压力等。浆液流动于岩体的裂隙网络,不同的裂隙网络对注浆效果有很大的影响,影响因素有裂隙开度、渗透系数、裂隙间距和夹角等。目前,注浆设计的制定主要依据现场试验和理论分析。现场即通过室内外的模型试验获取试验数据,基于实验数据分析注浆参数对注浆效果的影响,理论分析则通过建立浆液的扩散模型选取微元结构求解力学方程得出注浆参数的理论值。
关于裂隙注浆理论,国内外学者进行了广泛研究。杨秀竹等[1-2]基于广义达西定律及球形扩散理论模型对宾汉浆体和幂律型浆体在岩土中渗透扩散半径的计算公式进行了推导,分析了浆体性能参数对注浆压力和扩散半径的影响;王强等[3]基于宾汉流体渗流模型,推导出裂隙注浆中注浆量计算公式;周子龙等[4]基于Navier-Stokes方程建立宾汉流体的本构模型推导幂律型浆液在平板裂隙中的扩散半径和压降方程;张庆松等[5]通过开展水泥—水玻璃(C-S)浆液单一平板裂隙动水注浆模型试验,揭示了基于试验条件下的C-S浆液裂隙动水注浆扩散过程的扩散规律。但上述研究均基于单一裂隙的浆液流动规律,实际工程中的裂隙网分布复杂裂隙交叉及分布大大影响了浆液的流动。刘滨[6]自主研发了单裂隙和交叉裂隙网两个可视化注浆实验平台,研究了浆液参数和裂隙几何参数对浆液扩散的影响规律。当前的注浆理论研究中,虽然探究了在理论上研究出在一定限定和假设条件下浆液在裂隙中的扩散规律[7-10],部分也考虑了渗流对应力场的影响[11-13],但是都没有考虑到由于注浆初压以及浆液扩散对裂隙宽度产生的影响,而隙宽产生的位移扰动对渗流场产生的影响不可忽视。
为解决上述问题,本文基于宾汉流体的本构模型,引入传递矩阵算法深入研究裂隙岩体注浆过程中浆液流场引起的裂隙开度变化,建立考虑裂隙开度变化的裂隙注浆扩散理论模型,同时分别考虑浆液在裂隙内和岩体中的压力梯度方程,突破了只能在单一裂隙内研究浆液扩散的弊端,进而完整描述了浆液在裂隙及岩体内的整体扩散过程,这对于实际工程中提高注浆效果有实际意义。
1 裂隙浆液扩散理论模型
浆液在假定的裂隙中的扩散运动示意见图1。图1中:r0为注浆孔半径;R为扩散半径;v为浆液流动速度;p为浆液扩散压力,取x方向为浆体的流动方向。本文为了定量地研究浆体和裂隙参数如裂隙开度、渗透系数和浆液自重等对压降和扩散半径的影响规律,特进行以下假定:
(1) 浆液为不可压缩、均质、各向同性的宾汉流体。
(2) 裂隙上下侧壁无滑移边界条件成立,即上下侧壁处浆液流动速度为 0。
(3) 裂隙两侧岩体只发生弹性变形。
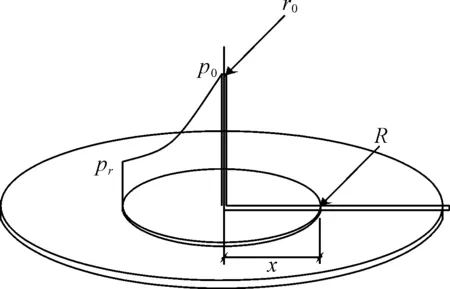
图1 管状裂隙模型图
1.1 浆体压降分析
利用Navier-Stokes方程描述流体微元的本构方程:
(1)
(2)
(3)
式中:vx为浆体在x方向的速度;vy为浆体在y方向的速度;p为浆体流动方向所受的压力;ρ为浆体的黏度为浆体的密度。
假设浆体是二维水平流动,即vy=0 则连续介质方程简化可得:
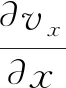
(4)
考虑到浆液的自重及裂隙倾角,将微元体本构方程中的内力取:
fx=ρgsinα,fy=ρgcosα
(5)
将式(5)代入式(1)、式(2)经过整理简化可得:
(6)
(7)
从N-S化简后的方程可以看出:垂直浆液流动方向的压降等于y方向的体力与浆液密度的乘积,沿浆液流动方向的压降等于速度在半径扩散的加速度与黏度的乘积与浆液重度沿水平方向的分量的和。为简化计算取:
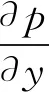
(8)
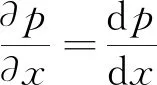
(9)
(10)
由式(10)可得浆液在水平方向上速度的关系式:
(11)
对式(11)中的变量y进行二次积分,积分区域为裂隙宽度范围0~b,可得浆液流速的方程式如下:
(12)
进而求出浆液在裂隙中单位时间内填充裂隙的浆液量q:
(13)
由上式得出在水平方向的压力梯度:
(14)
对式(13)进行积分并将x=r0,p=p0作为边界条件代入上式得:
(15)
1.2 扩散半径分析
重新从式(15)解得单位时间内的注浆量q:
(16)
根据单位时间注入裂隙的注浆量和扩散半径增大所需流量相等,可以得到注浆扩散半径,即:
(17)
经过化简计算最终得出扩散半径与压降、浆液粘度、裂隙倾角和裂隙间距之间的关系式:
(18)
当t=T时,r=R即:
(19)
2 裂隙注浆的传递矩阵算法
本文提出引入传递矩阵法,可以定量计算由于注浆压力及裂隙间的相互作用引起的不同位置处裂隙的开度变化量,将经过扰动后的裂隙开度重新代入扩散方程即可得到更为精确地得出扩散半径方程。
2.1 传递矩阵原理
传递矩阵法[14-18]为一种半解析数值方法,其基本思想为把结构整体离散成若干单元,每一个单元的各种形状参量,都会形成该单元的状态矢量。而且,这些单元之间由于相互作用的关系,前一个单元的变化会引起后一个单元的变化,这种变化依次类推,这样首端单元状态矢量发生的变化会一直传递给末端,设第i个元素的状态矢量是一个列向量Zi,而第i+1个元素和第i个元素之间的相互作用,用一个矩阵Ti来表示,则两单元的关系为式(20)。如果整体有n个单元,则有式(21)。
Zi=Ti-1Zi-1
(20)
Zn=TnTn-1…T1Z0=TZ0
(21)
式中:Ti被称为第i个子传递矩阵。而T被称为总传递矩阵。现在将岩体裂隙系设定为该整体,自变量为该体系的深度z,这种情况下,初始的状态向量就会沿着z方向传播。
2.2 多层结构体系应力及变形
将浆体在裂隙内流动过程中对裂隙壁的压力等效为矩形荷载P0,该作用力层层传递到每个裂隙上。假设裂隙在岩体中等距离分布,因此岩体中的裂隙分布见图2。
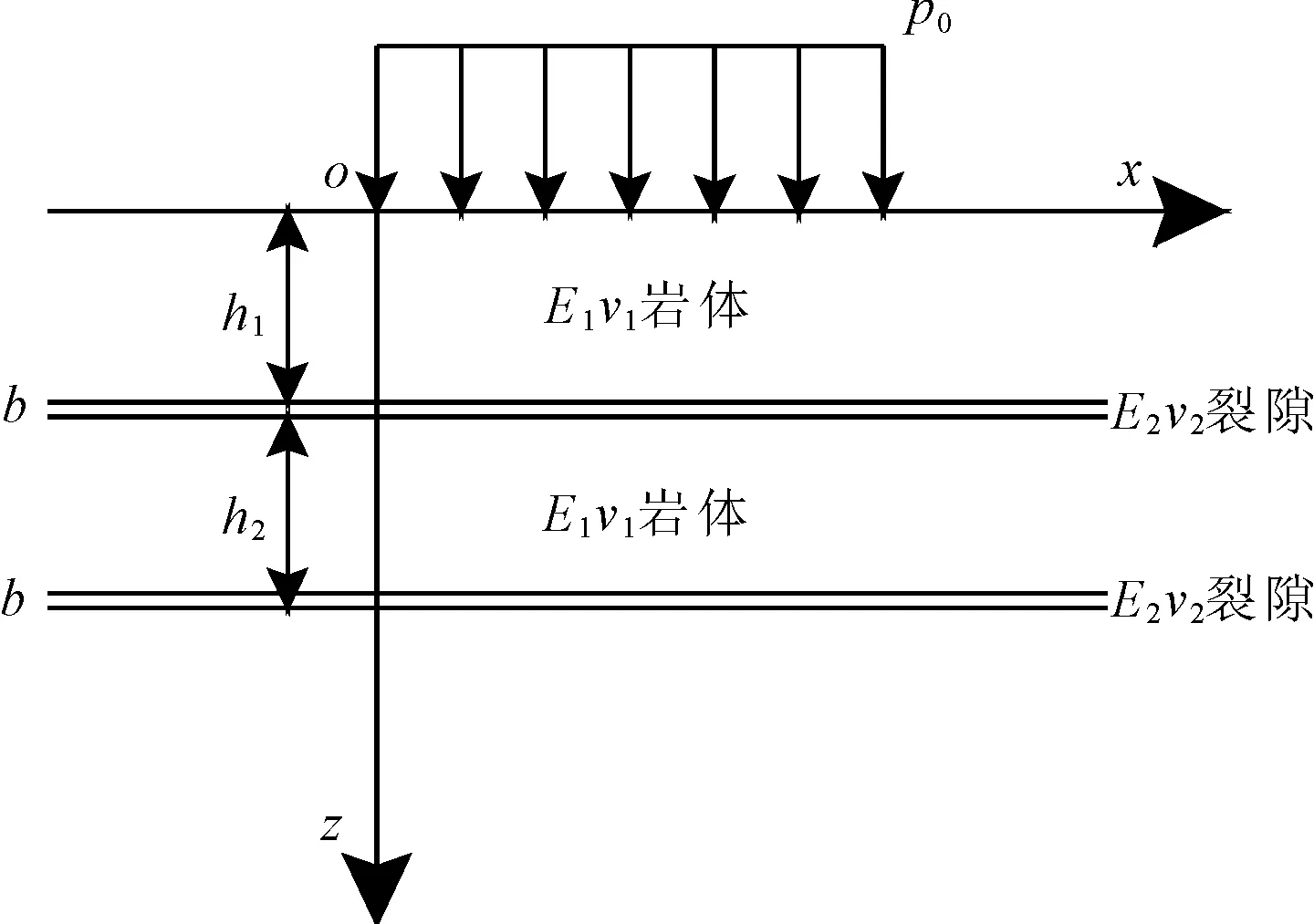
图2 岩体裂隙位移传递图
岩体的弹性力学参数为E1υ1,节理的弹性力学参数为E2υ2。第i层的深度为zi,每一层的层高为hi,裂隙岩体内摩擦角均设为为α。每层之间的传递矩元素如下:
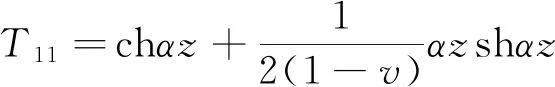
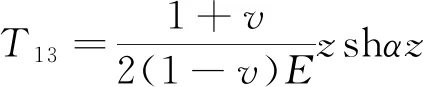
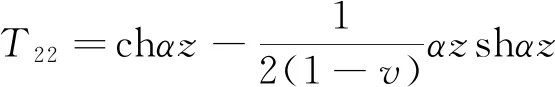
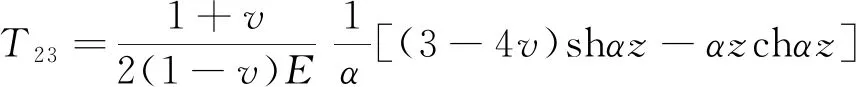
T24=-T13
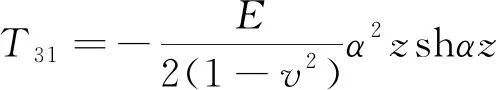
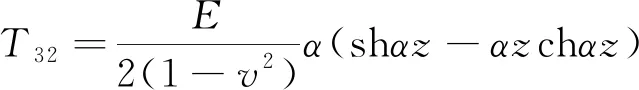
T33=T22,T34=T12
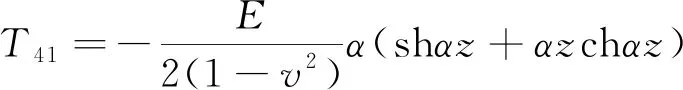
T43=-T31,T43=-T21,T43=T11
则每层间的传递矩阵为T=T(E,v,z,α)
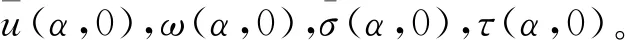
(23)
(24)
在公式的计算过程中,需要用到贝塞尔函数积分以及矩阵的相关复杂计算,因此需要对这一部分计算进行计算机编程,采用MATLAB软件编写了辛普森复合进行积分,从而较为精准的求解出由于上层的浆体流动对下层裂隙岩体的位移扰动量。将矩阵位移法得出的不同位置处裂隙开度用b′=b+w(w≤0)(w为矩阵计算后的裂隙竖向位移)来表达。
由于传递矩阵算法考虑到了裂隙及裂隙间岩体的相互作用,而浆液的扩散方程只是建立在管状裂隙模型中,为更完整的描述浆液在注浆压力作用下突破裂隙之间岩体阻力在裂隙及岩体完整的扩散过程,本文建立浆液在岩体间劈裂注浆的简化模型即假定裂隙在岩体中的扩散模型与平板裂隙相同只是加设阻力来模拟浆液在岩体内扩散的能量耗损。由于浆液的扩散主要受到注浆压力的作用,因此认为浆液在岩体中扩散时受到阻力,即视为浆液通过劈裂注浆需要耗损部分能量,阻力值参照裂隙和岩体的力学参数比值设定如下:
(25)
从而得出浆液在岩体间的压降方程式(26),为求解浆液在裂隙和岩体中的压降方程,现将一条裂隙和裂隙间的一组岩体作为在压力扩散方程的新的扩散模型,在该模型中压力梯度方程变为在裂隙中的压力梯度和岩体中挤密扩散压力梯度之和式(27),由上式可以算出新的压降公式(28),最终将得到的新的裂隙开度及压降方程代入上述推导的扩散半径方程后得到浆液在一组裂隙和岩体中的扩散半径方程。
(26)
(27)
(28)
(29)
上述理论模型可以通过传递矩阵法计算出距离注浆位置任意位置处的实际裂隙开度和压降值,最终得到任意浆液扩散锋面处浆液将会产生的扩散半径。考虑到当前实际工程中常应用改变注浆压力的变参量注浆方法,此模型可以快速得出浆液扩散锋面处浆液的扩散半径,进而控制注浆压力或者注浆量的改变来获得良好的注浆效果。因此该理论模型对于实际工程具有参考意义。
3 裂隙岩体注浆数值模拟验证
3.1 建立数值模型
为验证上述理论模型的正确性,本文建立了三维有限元分析模型模拟浆液在裂隙中的扩散。该软件是以有限元法为基础,通过求解偏微分方程组来实现多物理场仿真计算。其中的CFD模块可以定义和研究流体流动系统,在结构力学模块中选取岩石力学模块来模拟岩体和裂隙。为研究注浆扩散动态过程,采用流体力学模块与固体力学模块进行多物理场瞬态耦合计算。
该模型由三部分组成,模型中间为裂隙,裂隙上下均为岩体,裂隙单侧岩体厚度为 0.5 m,半径为 1.5 m,岩体上方留有半径为0.2 m的注浆孔。建立单条裂隙和两条裂隙模型进行裂隙岩体简化模型进行量化的数值校核,见图3、图4。
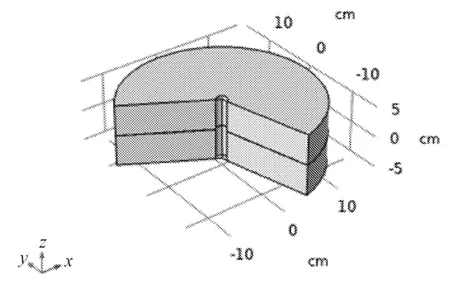
图3 单裂隙岩体模型
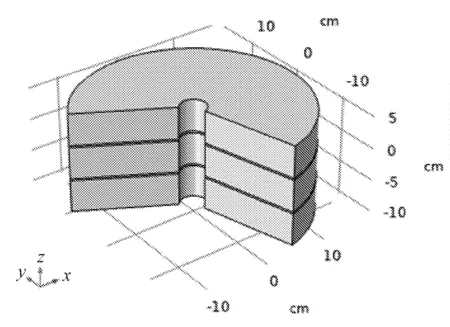
图4 多裂隙岩体模型
3.2 边界及网格剖分
岩体上下为固定边界,四周为棍支撑边界,而裂隙内壁为无滑移边界,与岩体接触面则均为无流动边界,均满足无滑移边界条件。初始时刻在注浆孔处以恒定压力注入,注浆开始后浆液进入裂隙流动。模型网格采用细化自由 4 面体网格,最小单元尺寸为 0.02 mm,最大单元尺寸为 4 mm,曲率解析度为 0. 25。为提高计算精度,在裂隙附近采用加密网格见图5、图6。
3.3 计算工况
设定初始的裂隙开度为0.3 mm,采用恒压注浆的方法,在注浆口处施加0.3 MPa的注浆压力,浆液选取水灰比为1∶0.7,浆液密度为2 500 kg/m3,浆液的黏度按照水灰比取7 MPa·s。岩体的弹性模量为30 GPa,泊松比为0.3,密度为3 000 kg/m3,裂隙的弹性模量为10 GPa,剪切模量取3 GPa。
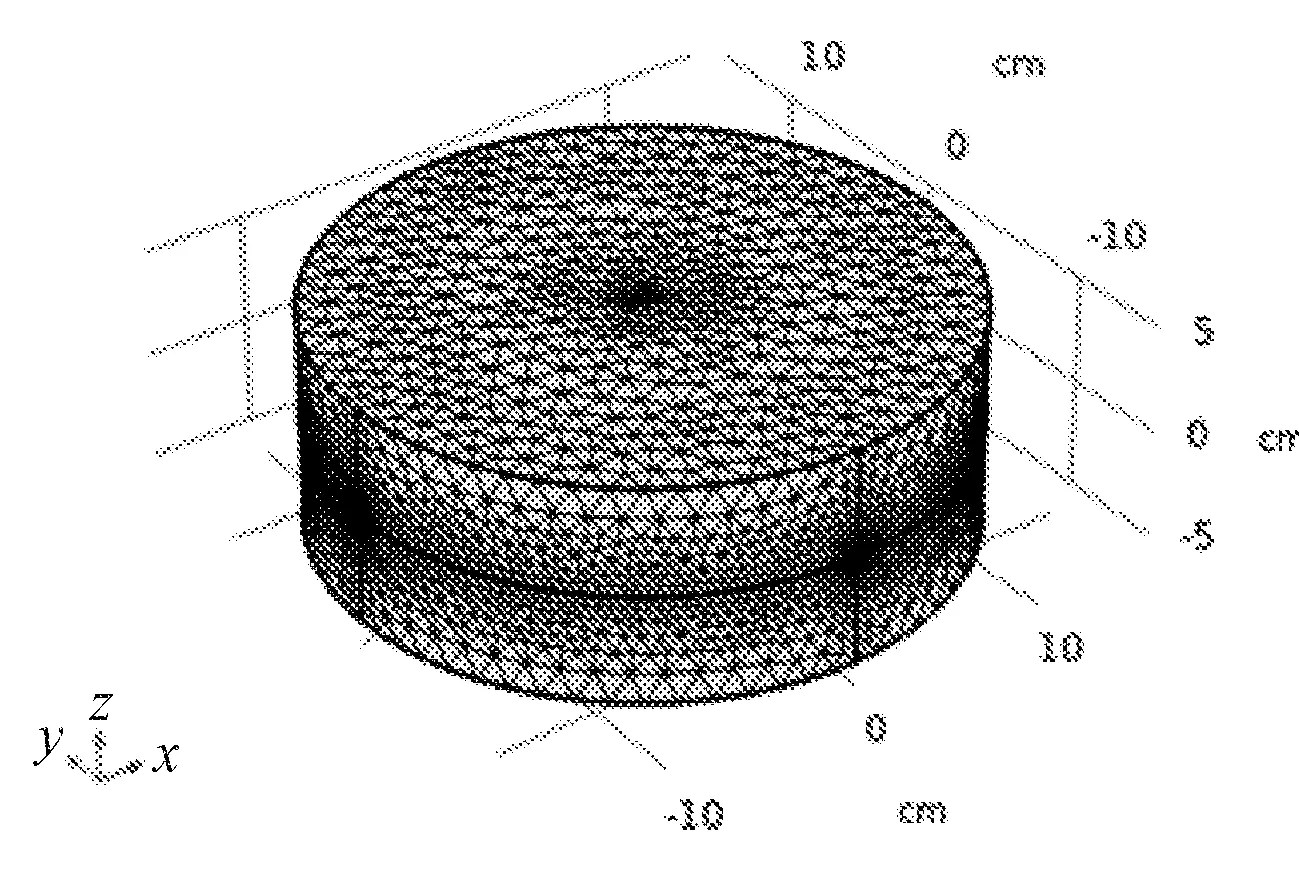
图5 单裂隙岩体网格划分
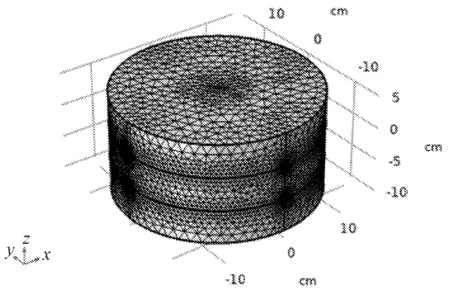
图6 多裂隙岩体网格划分
3.4 数值验证
经模拟发现当注浆时间为12 s时,裂隙的开度变化达到最大且浆液已充分流动至裂隙边缘处。以下分别为刚开始注浆时和浆液运动10 s后的单裂隙注浆模型裂隙位移变化图(见图7、图8),由图示可知浆液流动过程中裂隙位移逐渐变大,当浆液扩散至裂隙边缘处裂隙位移值达到最大。基于上述建立的裂隙岩体模型中计算与拟合基本保持一致。为了验证传递矩阵算法模型中的多裂隙岩体注浆模型的正确性,在Comsol建立多裂隙模岩浆耦合模型进行数值校核。在该模型中模拟过程中监测裂隙开度的时空变化,并将其与传递矩阵算法的裂隙注浆模型进行量化对比。
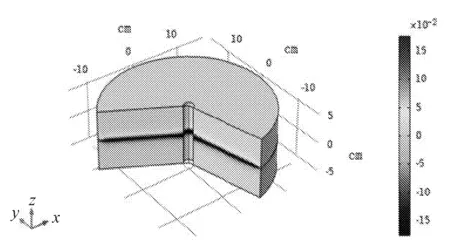
图7 注浆初始裂隙开度变化
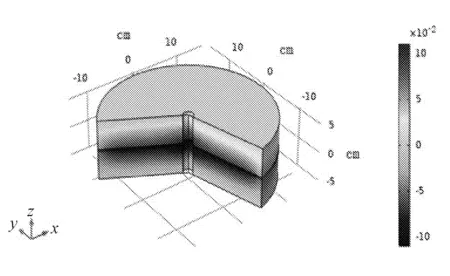
图8 注浆10 s单裂隙岩体位移
图9描述了距注浆位置较近的裂隙随着浆液扩散的开度变化,图10则描述的是下层裂隙的隙宽变化。可以看出裂隙网的隙宽都随着浆液扩散不断增大并最终趋于稳定。上层裂隙因距注浆孔位置较近收到注浆压力和浆液流动挤压的双向受力因此裂隙开度变化较大,下层裂隙从图10看出在浆液扩散至0.6 m处才能监测到隙宽变化,并且变化速率下降较快,趋近于某一固定值。在注浆时间为10 s时,考虑到由于浆液流动时间较短,浆液扩散距离相对较小,下层裂隙的裂隙开度变化主要受注浆压力引起的初始隙宽改变和浆液流动产生的挤压影响,因此注浆时间为10 s的下层裂隙隙宽基本没有发生变化。由图9、图10可以看出模拟得到的裂隙位移变化与推导结果有较好的一致性。因在相同注浆条件下,基于传递矩阵算法获得的扩散距离、裂隙开度变化规律与推导结果表现出非常好的一致性,说明基于传递矩阵算法的裂隙岩体模型能够将浆液扩散过程进行准确表达。
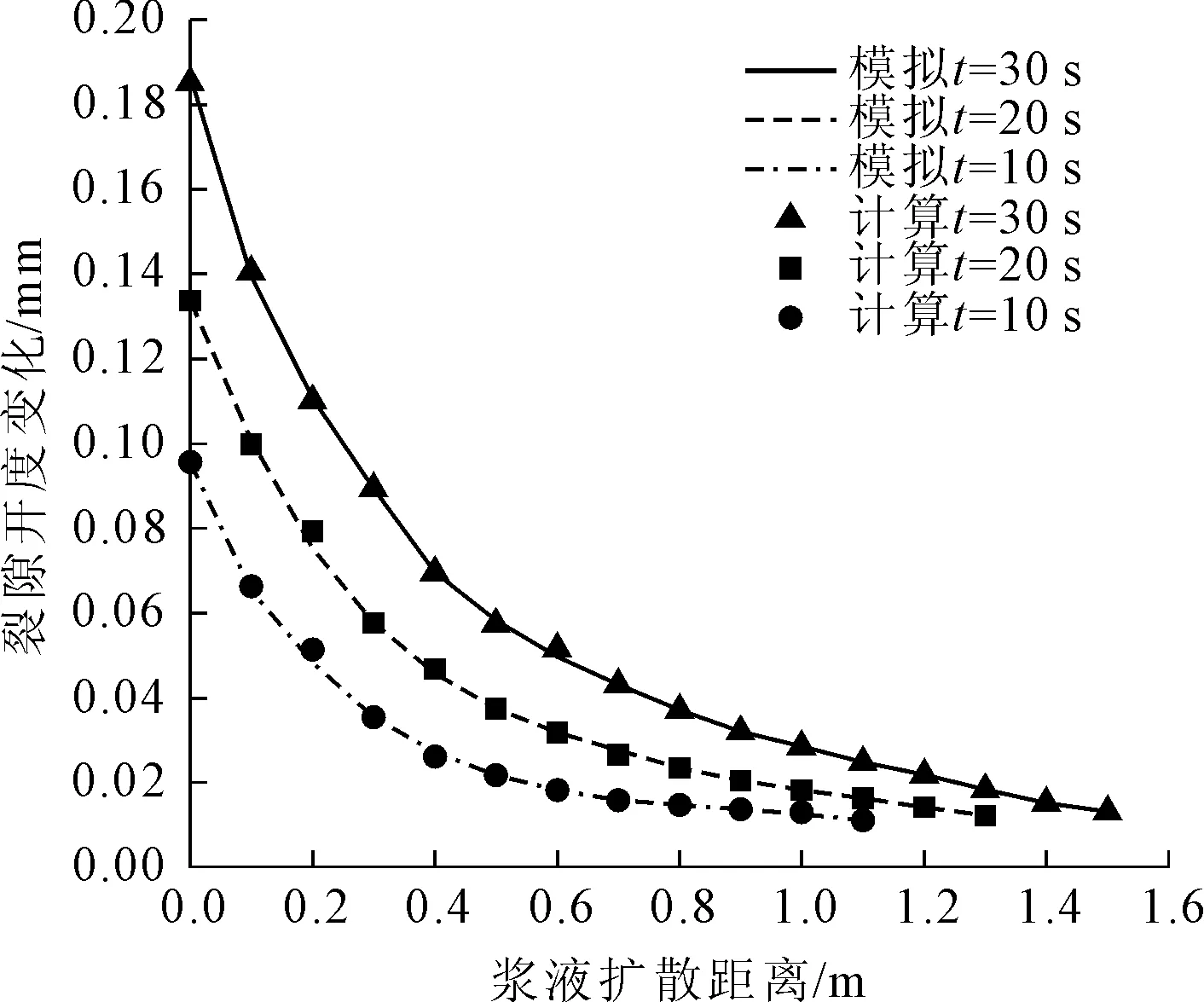
图9 上层裂隙开度随浆液扩散变化
图11描述了注浆压力为0.3 MPa的恒压注浆工况下浆液扩散距离与时间的关系,可以看出在注浆压力恒定的情况下,浆液扩散半径随时间的增大而不断增大,变化速率表现出先增大后逐渐稳定的趋势。将拟合得到的扩散半径与公式(29)进行校核对比,结果说明裂隙岩体组模型可以对恒压条件下平板裂隙注浆过程进行完整的描述,本文建立的基于传递矩阵算法的裂隙岩体简化模型基本准确。
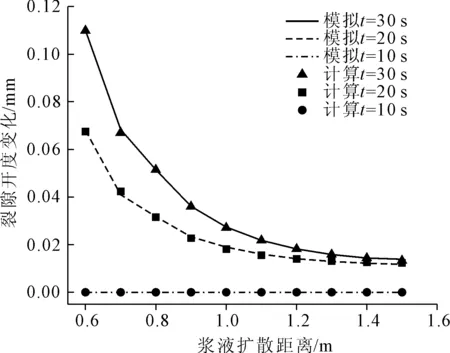
图10 下层裂隙开度随浆液扩散变化
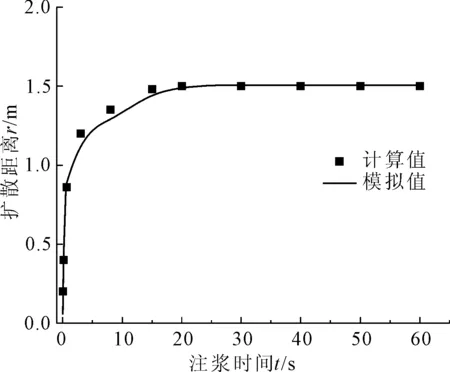
图11 浆液扩散半径随时间变化
4 结 论
(1) 基于上述模型引入传递矩阵法计算由于注浆压力引起的裂隙的微小位移,为突破当前局限于一条裂隙分析浆液的缺点,建立浆液在岩体间劈裂注浆的简化模型即假定裂隙在岩体中的扩散模型与平板裂隙相同只是加设阻力来模拟浆液在岩体内扩散的能量耗损。从而建立了可完整描述浆液在裂隙和岩体内连续扩散的理论模型,能够快速计算出浆液在扩散到各个裂隙位置处将产生的扩散半径。
(2) 应用有限元软件Comsol分别建立单裂隙、多裂隙注浆模型对上述理论模型进行对比验证。在模拟过程中可以看出裂隙的开度变化随着浆液扩散不断增大,并且距离注浆孔近的裂隙开度变化较大,而距离远的裂隙则开度变化并不明显。将浆液和裂隙的不同时空数据进行拟合后与上述算法进行比较,发现在相同注浆条件下,基于传递矩阵算法获得的扩散距离、裂隙开度变化规律与推导结果表现出非常好的一致性,说明基于传递矩阵算法的浆液扩散分析方法能够将浆液扩散过程进行准确表达。

