特定沉降阶段的盾构隧道地表沉降研究
谢铁军,刘 珍,杨果林,徐浩栋,吕 涛
(1.中建五局土木工程有限公司, 湖南 长沙 410004; 2.中南大学 铁道学院, 湖南 长沙 410075)
随着我国城市化进程的不断加快,既有城市的地面空间开发趋于饱和,对地下空间的开发和利用被提上日程。其中,以盾构隧道为主要技术建设的一系列地铁工程等项目在各大城市发展迅速。除此之外,作为铺开未来地下综合管廊一体建设的前提条件,基于盾构技术的地下管廊建设也成为地下空间开发的重点方向。相比于应用较为广泛的地铁隧道,以小半径为主的地下管廊隧道的工程实践经验不够充足,存在诸多问题。与一般的盾构隧道相比,其施工过程中引起周围土体的扰动变形规律尚待进一步研究。并且盾构施工引起土层变形会对周边邻近建筑物有一定的潜在危害。因此,研究探讨盾构施工过程中特定阶段的地表沉降规律,对于施工扰动控制和减少对周边环境的危害具有重要的意义。
目前,对盾构施工引起的地表沉降研究比较丰富。其中,常见的方法有理论分析法[1-3]、经验公式法[4-6]、数值模拟分析法[7-9]、现场或室内试验法[10-14]等。其中,邱明明等[7]建立三维盾构施工有限差分模型,对盾构施工地层竖向变形以及水平变形的计算结果对比分析,给出盾构施工引起的地层损失预测方法。杨泽飞等[3]在已有盾构施工后横向地表沉降算法基础上,提出了隧道周围土体的初始超孔隙水压力计算方法,研究了地表沉降速率随时间的变化。郭玉海[6]对某大直径隧道进行地表变形监测,分析检测数据和盾构掘进参数,得出隧道埋深、上部土层条件等因素对地表沉降影响较大。唐晓武等[2]利用通过坐标变换经积分推导盾构施工引起的总地面变形计算公式,研究发现计算公式在在盾构机头前后2L距离范围内较为适用。上述研究未深入考虑对盾构施工时施工因素对土体扰动变形的影响。因此,利用有限元分析软件,建立不同施工因素条件下的数值分析模型,对深入了解盾构施工过程土体变形规律具有重要意义。
本文以某电力隧道盾构施工过程为研究背景,针对施工过程进行现场地表沉降监测,采用ABAQUS软件建立盾构开挖数值分析模型,探讨盾构开挖过程中掘进推力,注浆压力,盾构机外壳与土体摩擦等因素对地表横向和纵向沉降影响规律的影响,为盾构施工沉降控制提供合理依据。
1 地表沉降阶段划分及计算方法
1.1 地表沉降阶段划分
通常而言,盾构施工过程中对于周围土体的扰动具有时间和空间效应。由此产生的土体变形以及地表沉降规律具有阶段性特征。根据Mair等[15]提出,根据盾构机推进过程以及盾构机相对土体位置,一般可以把受盾构推进扰动的地层沉降过程分为5个阶段见图1。
第一阶段,早期沉降。由于盾构掘进过程中,对土层地下水位的扰动,导致盾构前方土体在一定范围发生排水固结沉降。
第二阶段,掌子面沉降。此时盾构刀盘未到达沉降土体下方位置,刀盘推进压力产生的挤土作用和刀盘扭矩产生的扭转切削作用会导致前方土体发生形变。当刀盘推进压力较大时,产生挤土效应,前方土体发生隆起,反之则沉降。
第三阶段,通过时沉降。盾构机通过沉降土体下方,盾壳与土体接触面积大,推进时产生的较大的环向摩擦力,导致附近土体变形。
第四阶段,盾尾脱出沉降。在盾尾通过沉降土体后,尾刷和衬砌之间存在设计空隙引起一部分土体损失。此部分土体损失导致的地表沉降变形的主要来源。
第五阶段,土体次固结沉降。盾构通过后,部分土体随时间的变化,超孔压消散,继续发生流变变形,表现为一种长期沉降。
1.2 特定阶段的地表沉降计算
在上述的五个沉降阶段中,早期沉降由于开挖扰动产生的地表水位下降引起,在计算时随不同的水文地质有较大变化,且沉降量一般较小。在保证土压平衡的掘进过程中,掌子面沉降受刀盘推力设置影响有限。次固结沉降与土体的时间效应有关,一般对总沉降量累计影响不大。综合盾构机开挖实时扰动土体的空间位置以及沉降影响大小,主要研究讨论通过时沉降和盾尾脱出时沉降。
1.2.1 盾构机通过时沉降计算
Mindlin[16]在弹性半无限空间下,分别求出水平和竖直集中力作用下的应力和形变场。其中,当P为水平集中荷载时,任意一点的竖向位移公式为:
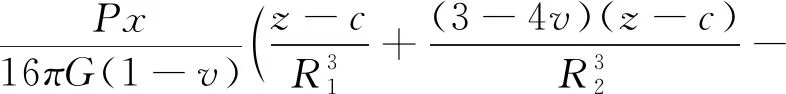
(1)
式中:P为盾壳和土体之间单位面积的摩擦力;v为泊松比;G为剪切模量取值可参考公式G=E/(2(1+u));E为弹性模量。
当P为垂直于y-z平面水平集中荷载时,根据式(1)得到x轴上竖向位移公式:
(2)
盾壳与土体之间摩擦力导致的地表沉降计算,将盾构机外壳看作圆柱体表面积分面积为dldθ,利用Mindlin解,对上式积分可得盾壳与土体摩檫力所引起的地表沉降计算公式。计算所取坐标系以及相关参数如图2所示。

图2 盾构机通过时沉降计算示意图
(3)
式中:p为盾壳与土体之间单位面积的摩擦力,p=μF/(πDL);μ为摩擦因数,黏土中取0.2~0.3,砂土中取0.3~0.4。F为盾构机与土体间摩擦力在总推力中的占比,根据文献[2]可取70%左右。
1.2.2 盾尾脱出时沉降计算
盾尾和衬砌之间存在设计公差,一般掘进过程中,土体损失主要发生在盾尾脱出管片这一阶段。Peck[17]提出地层损失是隧道开挖过程中发生地表沉降的主要原因,并提出了应用最为广泛的经验公式。
(4)
Sagaseta[18]认为盾构施工过程中土体损失等效看作邻近圆柱体,并给出了解析解。在原式基础上考虑盾构机进行修正可得:
(5)
式中:S(x)为地表横断面竖向位移大小;x为距离隧道中轴横向水平距离;Smax为地表最大变形,一般位于中轴线处;i为地表沉降槽宽度系数;Vloss盾构方向上单位长度的地层损失量;R为隧道计算半径;h为隧道中心埋深;g为等效土体损失参数,近似可取盾尾处与管片值径的差值。η为地层体积损失率,即单位长度地层损失占盾构开挖体积的百分比。
2 工程背景
长沙市万家丽路220 kV电力隧道起于万家丽路与特立西路西北角,止于万家丽路与火炬路交汇处西北角,全长5.957 km,隧道内径3.6 m,外径4.1 m。隧道推荐采用1.2 m宽管片,最小曲线半径位置采用1.0 m宽管片,管片厚度0.25 m,采用C50混凝土,主受力钢筋采用HRB400级。衬砌全环由一块封顶块K、两块邻接块L和三块标准块B构成,错缝拼装。
工程采用2台土压平衡盾构机,盾体长度约7.80 m,最大掘进速度8 cm/min,最大推力18 620 kN。适宜卵石层、砾岩交互层、淤泥质土、粗砂等土层的掘进施工,盾构机掘进最小曲率半径150 m。
现场布置监测断面区间为DK2155—DK2205。沿着掘进方向,在隧道中轴线上地表里程处,每隔5 m设置一个监测点。在DK2205处设置横向监测断面,此断面共设置13点,在前进方向轴线左右两侧设点,断面测点间距为距离轴线0 m、±3 m、±8 m、±13 m、±18 m、±23 m、±28 m。在同一个断面上取与隧道轴线相交的中心点为7号点,由中心点向东西方向编号1~13号监测点。
查阅相关地质勘查资料,施工开挖段土层自上而下主要分为四层:素填土、粉质黏土、卵石、全风化砾岩。各层土的力学参数如表1所示。

表1 土层力学参数表
3 盾构开挖沉降数值分析
3.1 基本尺寸及边界条件
ABAQUS作为一款三维有限差分元软件,在岩土工程领域有着较为广泛的应用,可以较好分析盾构隧道开挖模拟问题。利用ABAQUS有限元分析软件,进行小半径隧道开挖模拟。基本假定:土体为弹性半无线体,不考虑长期时间效应引起的次固结变形沉降问题。不考虑实际开挖中超挖和欠挖现象。
ABAQUS有限元模拟开挖模型采用摩尔-库仑模型。盾构机和衬砌均采用线弹性材料。整个模型主要由土体,盾构机,等代层,衬砌管片四个部件构成。各个部件都采用实体单元进行模拟,见表2,图3。
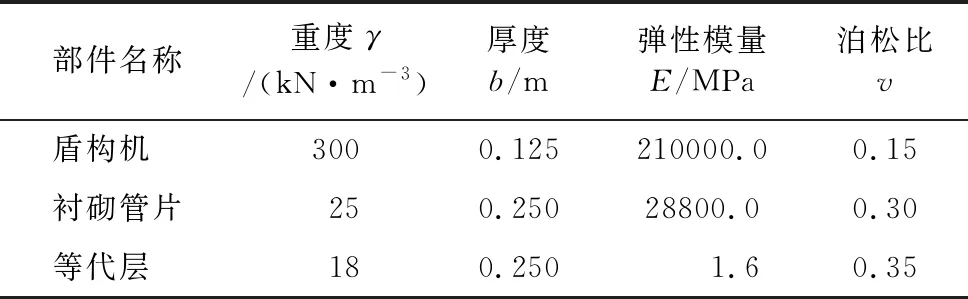
表2 数值模拟部件参数表
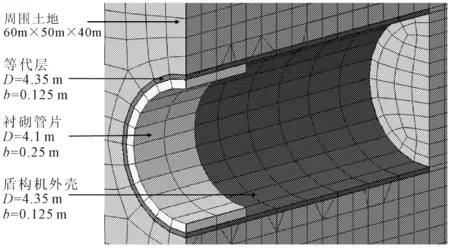
图3 盾构机通过时沉降计算示意图(开挖8环)
根据相关地勘资料以及现场数据,盾构隧道直径4.1 m,埋深19.2 m,盾构机只模拟外壳部分,外径4.35 m,厚度0.125 m。等代层外径4.35 m,管片外径4.1 m,宽度1.2 m,厚度0.25 m。构建开挖模拟模型的长宽高分别为60 m、50 m、40 m。整个模型划分出51 680个单元,57 834个节点,指定单元类型为C3D8(八个节点三维结构实体单元)。
模型四周边界限制水平移动,与x轴和y轴方向相交的面限制水平位移为零。与z轴方向相交的地面限制三个方向的位移均为零,顶面不进行位移约束。
3.2 模拟盾构掘进过程
在ABAQUS分析软件中利用Model-Change功能模块,即生死单元法进行开挖全过程模拟。主要原理是对模型的一部分进行删除或者激活,进行临时分析或是剩余部分的分析。由此结合实际开挖情况,可利用生死单元法模拟盾构土体的开挖。具体可分为以下几个步骤:
步骤一:准备阶段。预先设置好需要开挖的土体,按照每一次1.2 m的开挖深度进行划分。为满足模拟盾构机盾体行进过程,开挖7.0 m×1.2 m距离后,激活盾构机单元,此时再激活两片衬砌管片,模拟实际开挖过程中盾构机内部拼装过程。
步骤二:掘进阶段。完成开挖准备阶段后,盾构机向前挖1.2 m,“杀死”前方土体单元,激活对应的盾构机单元。“杀死”盾构机盾尾临时单元,此时盾尾脱出一片管片,激活对应管片外侧的等代层单元。
步骤三:拼装阶段。在掘进阶段完成后,在盾构机内部拼装下一环管片,此时只需激活下一环管片单元。保持其他单元状态不变。
此后,循环重复步骤二、步骤三。模拟实际开挖过程中掘进和拼装交替进行过程,完成全阶段的盾构动态开挖流程。具体开挖过程如图4所示。
为研究盾构掘进过程中不同施工因素对土体沉降的影响。分不同工况分别对开挖模式施加不同的附加力:
工况1,开挖只考虑掌子面推力因素,在全阶段都对掌子面前土体施加推力。
工况2,在工况1的前提下,考虑等代层注浆压力的因素。在盾尾脱出时,对环向土体施加0.4 MPa的注浆压力,注浆压力的效果持续五环。
工况3,在工况1的基础上考虑盾构机外壳与土体之间的摩擦。根据实际施工情况,对全过程盾构机外土体施加等效摩擦力4 900 kN。
在模拟开挖推进到第9环,即第二次盾尾脱出管片时,在掌子面截面上布置水平横向监测线。其距离地表的深度依次为0.0 m,3.4 m,9.4 m,15.0 m,由浅到深度分别编号为一至四号监测线。在沿着隧道开挖方向的正上方地表处布置纵向地表监测线,编号方式相同。
3.3 横断面沉降数据分析
不同深度位置处横断面竖向位移的变化曲线在三个不同的工况下如图5所示。此时盾构模拟开挖至第9环,开挖面位于监测断面正下方。在工况1、工况2下,随着施工推进,隧道上方土体向隧道中心塌缩,隧道中轴线位置产生最大沉降值。且最大沉降值随着检测线深度增加而不断增大,沉降曲线由地表处“U”形沉降槽,向“V”形沉降槽转变。埋深小处,沉降曲线形状“宽”,埋深越大,沉降曲线越“窄”。在曲线的边缘处会产生轻微的地表隆起。对比工况1、工况2下,工况1不考虑注浆压力时地表处最大沉降为1.5 mm,大于有注浆的工况2处地表沉降1.1 mm。但工况二随着埋深的增加,15 m埋深处最大沉降为2.7 mm超过工况1处2.3 mm。此时,注浆压力加速了隧道附近深层土的沉降变形。工况3横断面竖向最大沉降随埋深的增加而减小,且在15 m埋深处土体反而隆起,曲线呈现“M”形分布。此时,由于此工况存在盾构机头对周围土体的摩擦力,压缩前方土体使其产生了沿着开挖方向的变形以及连带剪切作用产生竖直向上的变形累积,最终表现为盾构机周围土体向隧道中轴处移动,“U”形曲线向“M”曲线转变,产生了“挤土效应”。Sagaseta计算曲线参照公式(5),取计算参数z=0,L=8.4 m,R=2.2 m,c=19.2 m,η=0.015。计算曲线显示最大地表沉降为1.1 mm,与工况2的1.0 mm较为接近,计曲线沉降槽宽度远大于25 m,曲线总体形状与工况3中三号监测线相近。

图4 模拟开挖过程示意图

图5 不同深度横向变形图(开挖到第9环时)
盾构机通过监测断面后,不同工况下横断面地表沉降图。此时盾构模拟开挖至第20环,盾尾脱出管片一环,位于监测线正下方。对比工况1和工况2,最大沉降点沉降值分别为-9.1 mm和-2.8 mm。盾尾脱出后及时进行管片注浆抑制了盾尾脱后短时间内土体损失造成地表土体变形,对控制盾尾脱出沉降有显著作用。实测曲线并未出现明显的反弯点,工况3地表沉降曲线由于模型边界限制在临近边界处出现反弯点。推测实际横断面地表沉降影响范围大于3 h。工况3由于盾构机头与土体的摩擦力作用挤压开挖面前方土体,导致开挖面后方土体应力释放,沉降值远大于工况1、工况2。其最大沉降值为-17.2 mm与实测曲线-16.9 mm较为吻合。Peck计算曲线参照公式(4),取计算参数h=19.2 m,R=2.2 m,φ=12.5°,η=0.015。Peck经验公式预测曲线中,沉降最大值为-9.5 mm,明显小于工况3和实测值,与工况1较为接近。Sagaseta计算曲线沉降最大值为-1.9 mm,明显不适用于盾尾脱出阶段的沉降预测(见图6)。
3.4 纵断面沉降数据分析
模拟隧道掘进第9环时,不同工况下纵断面不同监测线处沉降曲线图如图7所示。
开挖面前方,土体沉降变形主要发生在纵向距离h范围内,且只有工况3中土体产生隆起。工况3中,开挖面前土体沉降值随监测线埋深增加而减小,开挖面后土体沉降值随监测线埋深增加而增大。工况1、工况2随着监测线埋深增加,土体沉降不断增加。前三条监测线下,沉降发展较为平缓。在埋深15 m处,即离隧道埋深1D处,沉降曲线陡峭,并且曲线在盾尾处产生拐点。对比工况1、工况2,盾尾注浆使得开挖面后方土体沉降减小。对比工况2、工况3,盾构机与土体的摩擦作用使得开挖面后方的土体沉降增大。

图6 不同工况地表横向变形图(开挖到第20环时)

图7 不同深度纵向变形图(开挖到第9环时)
沿着隧道掘进方向上,以隧道中轴线所在平面为纵断面,不同工况下以及理论计算和实际测量的地表竖向变形特征如图8所示。所有曲线总体呈倒“S”形状,但起伏变化各不相同。对比3种模拟开挖工况,工况1、工况2只施加了盾构机掌子面推力,前方土体几乎无隆起,在开挖面后方和正上方的土体发生沉降变形。工况3由于存在盾构机和土体之间的摩擦力,开挖面前方土体有明显隆起,最大值为0.8 mm。计算曲线参照公式(3),取计算参数p=14.9 kPa,l=8.4 m,R=2.2 m,c=19.2 m,v=0.3,G=3.8 MPa。计算结果表明在开挖面正上方的地表沉降为0,沉降曲线挖面为轴线呈反对称分布,开挖面前方土体隆起,在距离0.6h处达到最大值1.5 mm。实测曲线土体最大隆起为0.92 mm,变化趋势与计算曲线较为相似。考虑在实际开挖施工过程中,测出沉降曲线为前期沉降与掌子面沉降叠加而成,其最大值应小于理想条件下的计算曲线。

图8 不同工况地表纵向变形图(开挖到第9环时)
4 结 论
(1) 利用Mindlin解推导沉降公式的和Peck经验公式可以较好的反映通过时地表竖向沉降和盾尾脱出后地表横向沉降。与实测结果相比,Mindlin解推导沉降公式未能反映早期排水沉降,导致结果偏大。Peck经验公式未能反应后期次固结沉降,导致结果偏小。Sagaseta推导的沉降公式在预测开挖面前方土体横向沉降变形有一定适用性。而开挖面后方土体受到前期盾构机摩擦力以及注浆压力作用后,沉降发展迅速。此沉降公式对于开挖面后方土体沉降预测的适用性较差。在实际使用过程中,可以考虑实际因素进行适当修正。

图9 地表变形三维图(开挖到第30环时)
(2) 通过时沉降主要影响纵向地表沉降,脱出时沉降主要影响地表横向沉降。不同工况下,在盾构机开挖面未达到监测断面时,地表沉降曲规律状无明显差异,最大沉降值之间相差不超过0.5 mm。可见施工掘进参数对早期沉降影响并不大。但在盾构脱出后,不同工况下地表沉降规律有显著差别,增大注浆压力和持续时间使得最大沉降明显减小。距离隧道1D范围内的土体沉降变化剧烈,2D范围外影响逐渐减落。
(3) 施工因素对于土体扰动有重要影响。增大注浆压力和持续时间,可以有效控制盾尾脱出阶段时产生变形。盾构机与土体的摩檫力主要影响盾构通过时的沉降,主要表现为前方土体隆起。施工时动态调节总推力的大小,保持开挖时土压平衡状态。有利于控制环向摩擦力,进而控制开挖面前方土体变形。

