早期受冻对混凝土耐久性劣化的影响研究
徐存东,高德坤,张 鹏,谷丰佑,李洪飞
(1.华北水利水电大学 水利学院, 河南 郑州 450046;2.浙江省农村水利水电资源配置与调整关键技术重点实验室, 浙江 杭州 310018; 3.河南省水工结构安全工程技术研究中心, 河南 郑州 450046)
在我国北方地区,冬季普遍存在低温的环境,最长可达5—6个月[1]。而北方大部分地区夏秋两季依赖水利工程进行灌溉,故只能在冬季施工[2]。然而,在冬季经常有气温骤降的情况发生,特别是在秋冬、冬春季节交替之际,刚刚浇筑的混凝土可能还未进行抗冻措施就因气温的巨大变化遭受冻伤或损坏,大大降低工程建筑的服役时间、承载能力、耐久性能[3]。我国北方早期建设的一些水工混凝土建筑物,已经存在不同程度的耐久性劣化,需要及时的进行修复和重建工程,否则有较大的安全隐患,可能造成不必要的经济损失。
20世纪末,国内外的专家学者提出了“抗冻临界强度[4]”的概念,用来描述混凝土受冻之后的性能。巴恒静等[5]研究了早期受冻对混凝土强度的影响,朱卫中等[6]研究了工程实践中混凝土耐久性的劣化原因。Powers[7]提出了静水压假说,认为是内部孔隙中未结冰的溶液受结冰的溶液挤压时,产生克服阻力的静水压力,导致破坏。Collins[8]认为受冻混凝土破坏是由于内部应力的重新分布而导致的,而Saul[9]与Nurse[10]用混凝土成熟度来描述成型后混凝土的耐久性。然而在比较复杂的工程环境下,受限于现场的条件等因素,难以对正在运行中的建筑物的各项性能指标进行直接测量。这些理论难以进行实际应用,故需要进行更具有现场实用性的探究。
本文模拟早期受冻环境,进行实验测试与分析,研究受冻温度、养护龄期等因素对混凝土服役期耐久性的影响。并建立抗压强度损失率和相对动弹性模量相关联的函数模型,以期为寒冷地区混凝土建筑物更新改造工程提供理论依据。
1 实验方案
1.1 实验材料与混凝土配合比
水泥选用P·O 42.5的水泥,该水泥的物理参数和各性能指标见表1。

表1 P·O 42.5水泥强度指标
细骨料选用细度模数为2.74的中砂,性能指标见表2。
粗骨料选用粒径5 mm~25 mm,表面粗糙且级配连续的坚硬石子[10],粗骨料的性能指标见表3。

表2 细骨料技术性能指标

表3 粗骨料技术性能指标
拌和水为自来水。混凝土配合比见表4。

表4 混凝土配合比
经过测试,此配合比[11]在自然环境下的初凝时间为90 min,终凝时间为480 min。
1.2 试验方法
本实验共设置8组试验组及一组对照组。尺寸为100 mm×100 mm×400 mm的棱柱体试块,每组5块,用于质量检测与动弹性模量的无损检测[12]。尺寸为100 mm×100 mm×100 mm立方体试块,每组21块,用于抗压强度的检测。设置方式见表5。混凝土拌合后,然后放入10 ℃的环境中养护至1.0 h、3.5 h、8.0 h、24.0 h后受冻6 h,模拟早期受冻过程,再放入养护室中,进行正常养护步骤。待养护完成后,进行冻融循环测试,每4 h为一个冻融周期,每经过25次冻融循环后,测量试块的质量Wn和动弹性模量Edn,每经过50次后,取出5块测试抗压强度。当质量损失率超过5%,或总体冻融循环次数达到150次,或相对动弹性模量低于60%时,停止实验[13-14]。
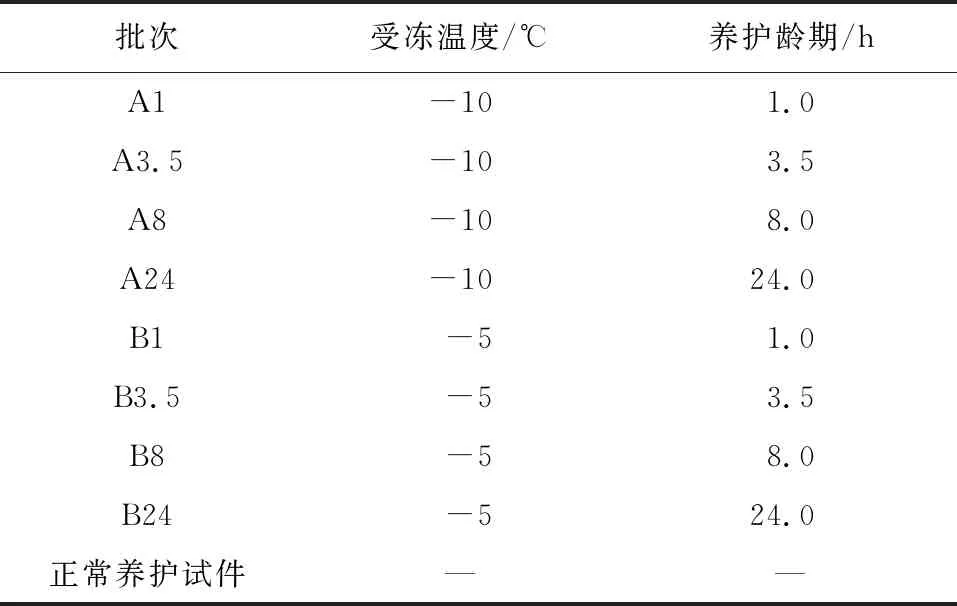
表5 混凝土试块分组
2 实验结果与分析
2.1 混凝土质量损失率变化规律
质量损失可以用来评价混凝土在受到冻融作用后的侵蚀情况。经过冻融作用后,试块质量损失率按式(1)计算。
(1)
其中:ΔWki为经过k次冻融作用,第i个试块的质量损失率;Woi为冻融前第i个试块的质量,g;Wki为k次冻融后第i个试块的质量,g。
则每组试块的平均质量损失率由下式计算:
(2)
其中:ΔWk为k次冻融作用后一组的平均质量损失率;n为每组的试块个数,为5。
根据以上公式可得到混凝土质量损失率,见图1、图2。
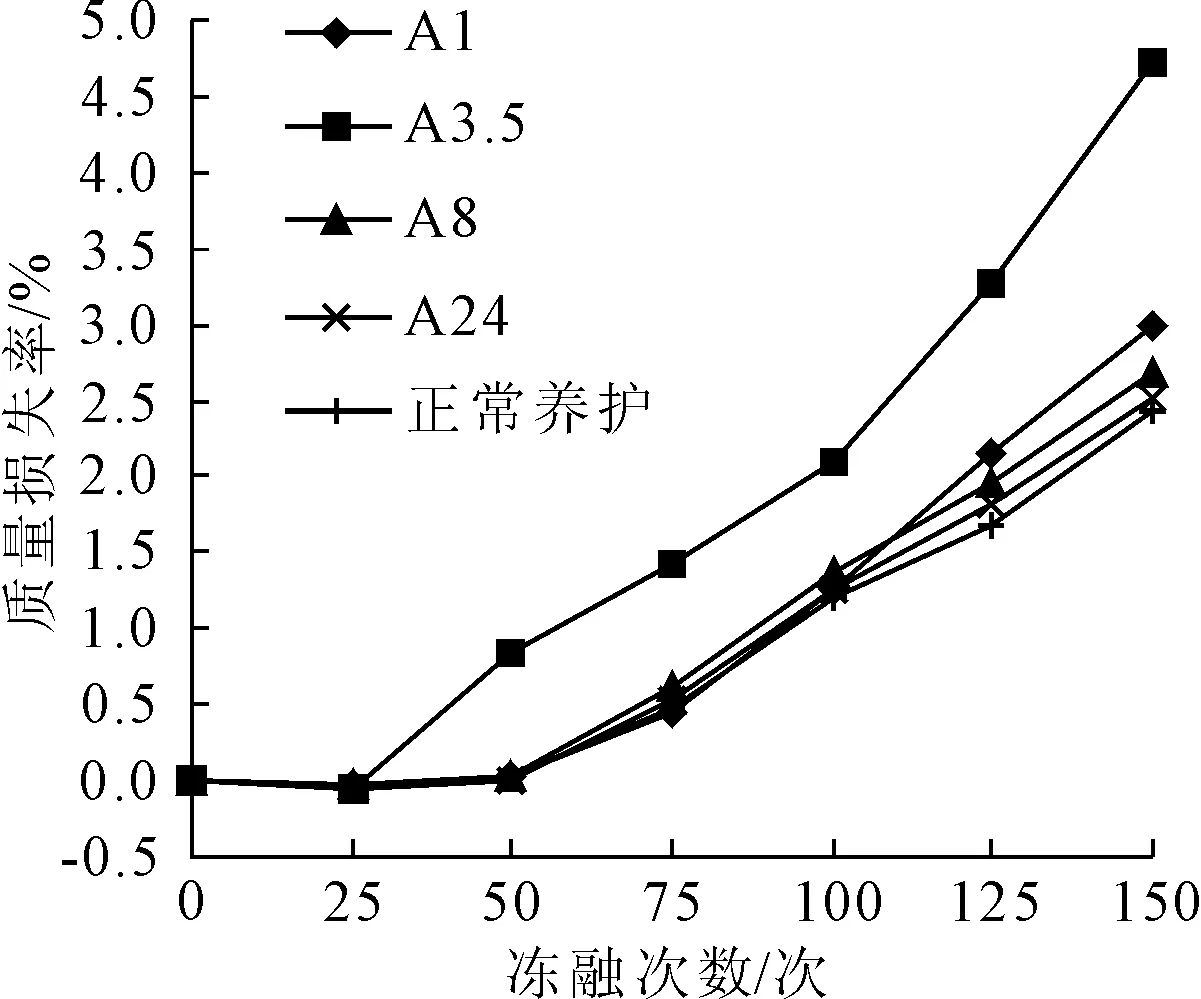
图1 混凝土质量损失率变化(A组)
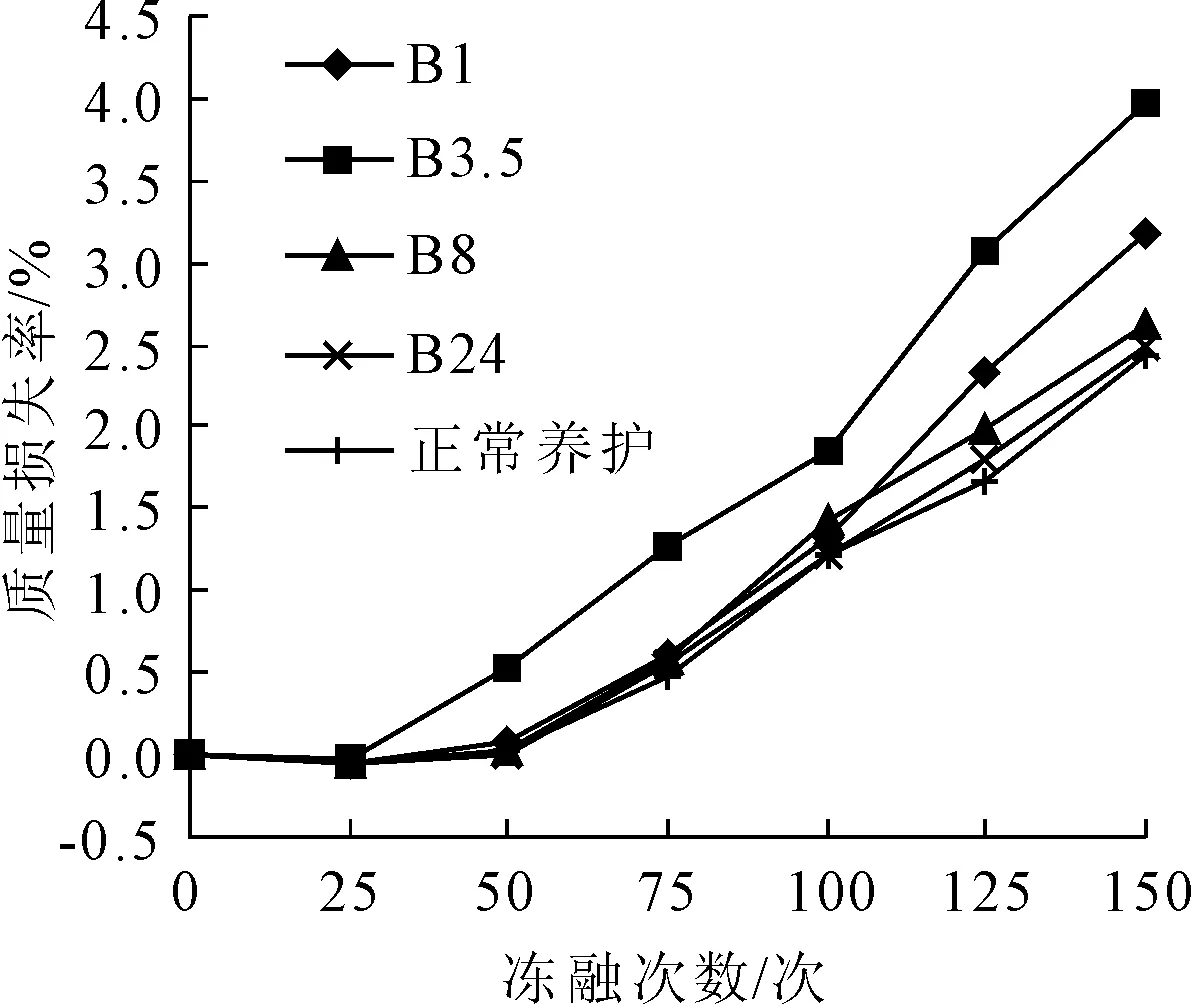
图2 混凝土质量损失率变化(B组)
2.1.1 养护龄期对混凝土质量损失率的影响
通过图1、图2的数据和曲线得知,对照组和各实验组的混凝土试块质量损失率均低于5%,在-10℃的条件下,质量损失率最高的为4.73%。A1和A8组质量损失率分别为2.98%、2.69%,A24组的质量损失率最小。在-5℃的条件下,试块具有同样的质量损失规律。随着冻融循环的进行,-10℃受冻的组别中,质量损失速度最快的是A3.5组,其他组别的损失速率较为接近。在受冻温度-5℃的实验组中,呈现的规律大致相同。质量损失率按养护龄期由高到低排序为3.5 h>1.0 h>8.0 h>24.0 h。
2.1.2 受冻温度对混凝土质量损失率的影响
当养护龄期相同、受冻温度不同的情况下,混凝土的质量损失率基本接近。分别对比A1与B1、A3.5与B3.5、A8与B8、A24与B24的质量损失率的差值可以看出,A1、A8、A24组之间的差值最大仅为0.2%,差距不大。而A3.5与B3.5组差值达到0.77%,显著高于其他实验组。说明初凝后到终凝前的这段时间受环境温度影响比较大,混凝土性能还不稳定。
当混凝土处于养护期时,养护龄期和受冻温度都可影响混凝土的初始损伤。在终凝前受冻的混凝土的损伤显著大于终凝后受冻的混凝土,此阶段内受冻的混凝土性能下降将最为明显。而受冻温度的不同对混凝土的影响较小,基本不影响混凝土的整体质量。
2.2 混凝土动弹性模量的变化规律
动弹性模量Ed可以较为简易的测量获得,是评价混凝土耐久性的重要指标[15]。动弹性模量的测量有超声脉冲法和共振法等方法,本实验采用共振法测定振动频率,再由式(3)计算得出结果。
(3)
其中:Ed为混凝土动弹性模量,MPa;a为试块正方形截面边长,mm;L为试块长度,mm;W为试块质量,kg;f为试块的基频振动频率,Hz。
为了直观的表现动弹性模量减少的程度,使用相对动弹性模量Erd,来评价混凝土的性能。按式(4)计算:
(4)
其中:Erd为混凝土相对动弹性模量,%;Edk为k次冻融循环后的动弹性模量,MPa;Ed0为初始的动弹性模量,MPa。
单个试块按以上公式计算后取平均值,得到每组的计算结果,汇总于图3、图4。
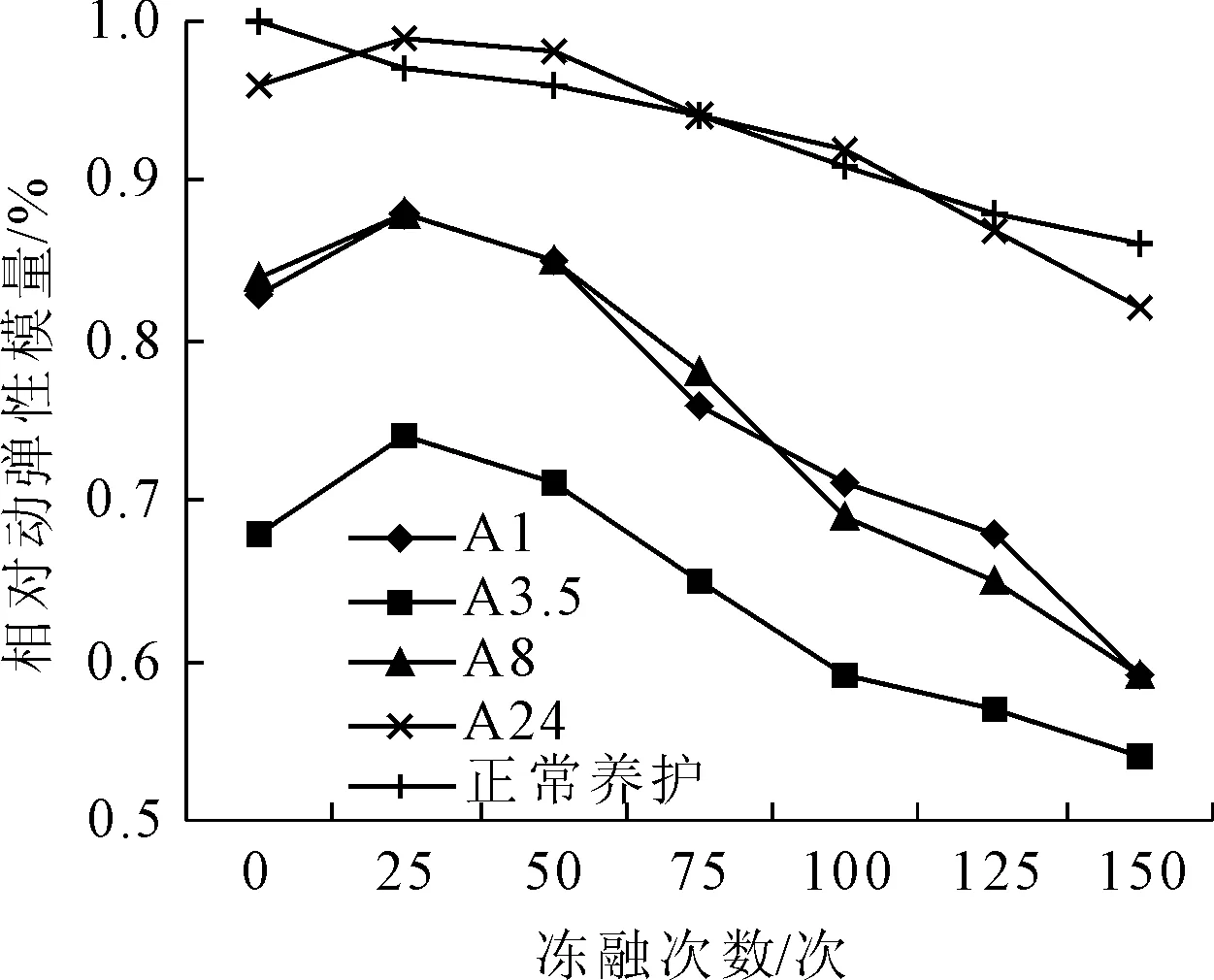
图3 混凝土相对动弹性模量变化(A组)
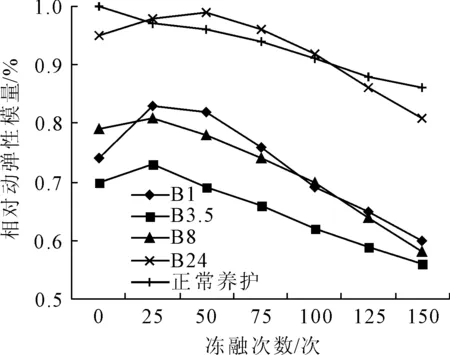
图4 混凝土相对动弹性模量变化(B组)
2.2.1 养护龄期对混凝土动弹性模量的影响
由图3、图4可以得出,还未受冻融循环作用的混凝土就因早期受冻的破坏,导致相对动弹性模量初始值就已经下降。其中A3.5组最为明显,而终凝后的A24组与正常养护基本接近。在冻融循环结束后,A1,A3.5,A8组的动弹性模量显著下降,均低于60%,混凝土性能显著降低。而正常养护的混凝土和A24组的下降程度不大。A24组受冻融作用导致的性能下降较小,可以正常工作。根据相对动弹性模量变化的图可以得知,各组试块的下降幅度和下降速度差别不大,说明不同养护龄期的混凝土都会受到冻融作用的影响。B组试块与A组情况比较相似,具有基本一致的变化规律和曲线特征。
混凝土性能劣化程度越高,相对动弹性模量就会越小,受到冻融作用的影响越大。初凝到终凝之间受冻的混凝土的相对动弹性模量较小。说明它们受到冻融影响最大。而终凝后的混凝土,性能比较稳定,受冻融作用的影响不大,与正常养护的混凝土差距不大。
2.2.2 受冻温度对混凝土动弹性模量的影响
当养护龄期相同、受冻温度不同的条件下,对比A1与B1、A3.5与B3.5、A8与B8、A24与B24组的相对动弹性模量下降情况可以发现,在冻融过程中,试块的相对动弹性模量变化差别很小。温度对相对动弹性模量的变化影响远远低于养护龄期对相对动弹性模量的影响程度。
养护龄期对于混凝土的动弹性模量的影响较大,还未受冻融的混凝土就会因养护龄期不同出现初始性能的损伤[16]。终凝前,混凝土内部的自由水因低温冻结成冰,在冻胀应力的作用下使得凝胶体开裂,混凝土的整体性遭到破坏,因早期受冻造成的初始损伤导致最终的相对动弹性模量较低,性能也会最差。
2.3 混凝土抗压强度的变化规律
抗压强度是指物体承受外力施加压力的极限,是用来评定混凝土的性能的主要指标之一[17-18]。抗压强度由式(5)计算:
(5)
其中:fcu为混凝土抗压强度,MPa;F为破坏荷载,N;A为承压面积,mm2。
每组5块试块的测试结果取平均值,以上公式的计算结果汇总于图5、图6。
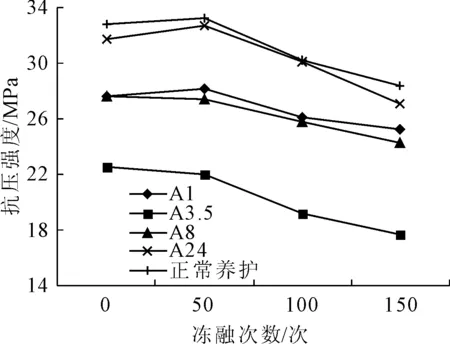
图5 混凝土抗压强度变化(A组)
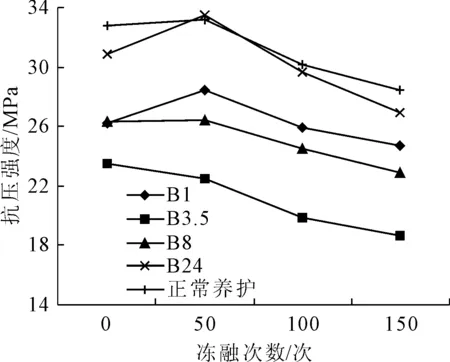
图6 混凝土抗压强度变化(B组)
2.3.1 养护龄期对混凝土抗压强度影响
由图5、图6可得,早期受冻可使试块的抗压强度降低。A3.5组在还未经冻融循环的情况下,抗压强度就仅为正常试块的69%。A1、A8组也均有下降。A24组下降不明显。在进行50次冻融循环之后,正常养护与A1、A24组的试块抗压强度有微小的增长。随着试验的进行,5组试块的抗压强度迅速降低。在结束试验后,A3.5组的抗压强度仅为正常值的54%。B组试块具有相同的变化规律。初凝后到终凝前受冻的混凝土在经过冻融循环后,随着冻融次数的增加,抗压强度下降明显。对于正常养护的混凝土,冻融作用也严重影响了其抗压强度,故冻融循环对于混凝土抗压强度的影响很大。
2.3.2 受冻温度对混凝土抗压强度的影响
对比A1与B1、A3.5与B3.5、A8与B8、A24与B24组的抗压强度变化数据与规律可得,两组对应养护龄期的试块数据差距不大,初始强度相差最大的A1与B1组仅为1.41 MPa,冻融循环后相差最大的A8与B8组仅为1.43 MPa,而A3.5组与A24组的初始抗压强度与试验后的抗压强度差值分别为9.17 MPa、9.41 MPa。说这明了受冻温度对混凝土抗压强度的影响远远小于养护龄期的影响。
早期受冻对混凝土抗压强度的降低影响非常明显,在冻融循环前,养护龄期不同的混凝土初始抗压强度的降低就比较明显。初凝到终凝之间受冻的混凝土,抗压强度较低,性能较差。而终凝后受冻的混凝土与正常养护的抗压强度比较接近。
3 相对动弹性模量与抗压强度损失率的相关函数模型
3.1 函数模型的建立
由上面分析可得,相对动弹性模量与冻融次数总体成反比例关系,单位冻融次数内动弹性模量损失率为常数。假设经过K次冻融循环的混凝土动弹性模量为Ed(K),此函数是可微的[19]。令φ1为常数(φ1<0),则由K到(K+ΔK)次冻融内,动弹性模量的损失率为:
(6)
移项得:
Ed(K+ΔK)-Ed(K)=φ1Ed(K)ΔK
(7)
即:
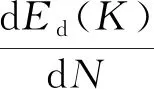
(8)
对上式积分得:
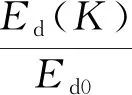
(9)
即:
Erd=eφ1K
(10)
变形得:
(11)
早期受冻的混凝土试块在冻融过程中,初期会因内部结冰等原因,造成抗压强度的微小提高[20],随后迅速下降,总体来看,抗压强度损失率与冻融次数为正比例关系。单位冻融次数下,抗压强度损失率为常数。假设经过K次冻融循环的混凝土抗压强度为fcu(K),此函数连续且可微。令φ2为常数(φ2<0),f0为试块初始抗压强度。则由K到(K+ΔK)次冻融内抗压强度的损失率为:
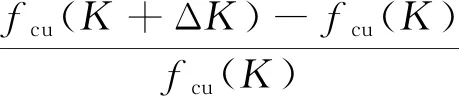
(12)
经过移项、积分、整理得:
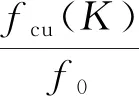
(13)
将式(11)代入式(13)中可得:
(14)
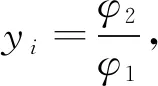
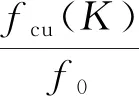
(15)
由式(15)可以得出,抗压强度损失率与动弹性模量损失率呈幂指数关系,由于抗压强度和动弹性模量的关系并未完全符合严格的正比例关系,故需要进行数据拟合,以得到xi、yi的值。
3.2 函数模型验证分析
研究相对动弹性模量与抗压强度损失率的拟合函数关系图,结果表明:不同养护龄期的混凝土动弹性模量与抗压强度损失率的R2均大于0.9,相关性良好,可以在现场测得动弹性模量的值,结合建造施工时的温度变化记录来推算抗压强度的损失情况。不同养护龄期对应的xi、yi见表6。

表6 相对动弹性模量与抗压强度拟合参数
4 结 论
(1) 养护龄期对混凝土耐久性劣化的影响很大,终凝前受冻的混凝土,质量损失最多,抗压强度和相对动弹性模量最小。耐久性能损失最大。终凝后的混凝土比较接近正常养护的混凝土,但仍有小幅度的性能损失。
(2) 受冻温度对混凝土耐久性劣化的影响较小,在不同受冻温度下,相同养护龄期的混凝土的质量损失、相对动弹性模量和抗压强度比较接近。
(3) 建立了相关性函数模型,证明了混凝土相对动弹性模量与抗压强度的损失率具有相关性,可通过易测得的动弹性模量来反映混凝土建筑物的抗压强度损失状况。进而判定建筑物的耐久性劣化程度。

