事故容错燃料结构对导热性能影响的计算

张海青 卢林远 王 鹏 严 超 林 俊

（中国科学院上海应用物理研究所 上海201800）

在核反应堆发展历程中，二氧化铀（UO2）核燃料由于具有熔点高（3 138.15 K）、非裂变组合元素氧的热中子俘获截面低（＜0.000 2 b）、在化学和结构方面具有较高的辐照稳定性，且制造费用较低等优势［1］，是轻水反应堆核电站广泛应用的核燃料。UO2作为核燃料的显著缺点是导热性能较差（7.7 W·m-1·K-1，300 K）［2］，仅为金属铀的十几分之一，这就降低了燃料芯块到冷却剂间的能量输出效率。这意味着它的工作温度相当高，约2 273.15 K。2011年日本福岛核电站事故揭露了UO2核燃料低热导率引发的核安全隐患［3］。在福岛核事故后，为提高核反应堆中燃料元件抵抗严重事故的能力，美国能源部发起了“研制和开发事故容错核燃料（Accident Tolerant Fuel，ATF）计划”［3］，这种燃料与标准的轻水反应堆UO2燃料锆合金包壳相比，在保持或提高反应堆正常运行工况下燃料性能的同时，当堆芯主动冷却系统功能丧失后，维持冷却状态的时间更长，安全裕度更高。

中国在响应国家安全高效发展核电的政策下，也启动了相关的研发计划，旨在通过研发事故容错UO2核燃料来推动新一代核燃料元件的开发与应用。此类燃料是通过在UO2燃料基体中添加高热导率的物质，如氧化铍（BeO）［4］、碳纳米管［5］或碳化硅（SiC）纤维［6］等，来提高其热导率，降低其工作温度。此类燃料体系的优势在于对工业制造体系的改动小、制造成本低。

目前，国内外关于事故容错热导率增强型UO2核燃料的研究关注点主要在于制备工艺的优化和导热性能的改善。而微观结构的调控是改善导热性能的主要手段之一。Pan 等［7］研究了短纤维填充橡胶复合材料中相邻两根短纤维之间的相互作用对应力分布产生的影响；金泉等［8］主要对颗粒和纤维混合填充橡胶材料进行了研究，得出了平行于加载方向的增强体受了很大的应力，随着纤维和加载方向之间夹角的增大应力减小；文献［9-10］研究表明，粒子间距是决定空间填料分布的一个重要参数，随着粒子间距离的增大，导热系数呈指数衰减；文献［11］研究了橡胶基体的填料粒子对复合材料热导率的影响。

实际上，复合材料的有效导热系数由许多因素决定，如颗粒的类型和形状、颗粒的排列方式、体积大小以及填料与基体之间的接触热阻。一般来说，用单纯的实验方法很难区分这些因素的影响。因此，模拟计算对于指导更好的热应用复合材料的设计和制造至关重要。本文将利用商用有限元软件Ansys Workbench，采用三维有限元分析的方法，通过模拟填充粒子的复合材料体积单元在特定温度边界条件下的温度、热流分布情况，分析在UO2燃料中添加BeO 纤维后，填料的几何形态、空间位置取向及填料空间堆积方式、颗粒大小等对热导率的影响。为事故容错燃料制备工艺的优化和导热性能的改善提供理论依据。

1 模型建立

1.1 热传导方程

对于各向同性材料，不考虑热源的稳态热传导方程为[12]：

式中：k 为热导率，又叫导热系数，热传导系数，W·m-1·K-1；T为温度，K。热传导问题的边界条件有三种：

式中：h为热交换系数；Te为环境温度。式（2）表示边界的温度值已知；式（3）表示边界的外法向热流密度值已知；式（4）表示热交换边界条件。

1.2 热导率

未经辐照、致密的燃料颗粒热导率k0为［13］：

综合考虑燃耗、孔隙度和裂变产物的影响，辐照下的颗粒热导率为：

式中：FD和FP分别为溶解和沉淀的裂变产物的影响因子；FM为孔隙度影响因子；FR为辐照效应影响因子；B为燃耗（已裂变原子数与总可裂变原子数的比值），%；P为孔隙度，%；s为孔的形状因子。

燃料颗粒和基体的热导率［14］为：

1.3 有限元模型

UO2颗粒在基体中的分布，可以近似为均匀分布，有限元模型可以将均匀分布设置成周期性分布的模型，即只需选取一个代表性体积单元来研究。根据均匀化理论，选取等效体积单元（Representative Volume Element，RVE）［6］，进而得到复合材料的均匀化参数。本文采用的是Ansys Workbench 稳态热分析模块，对于颗粒填充体系进行导热模拟研究。为提高其模拟的精确度选择3D模型最佳。本文基体材料均为UO2，填料粒子均为BeO 的复合材料，其中UO2和BeO 的热导率见文献［15］单胞上下面各施加不同的温度载荷，四周绝热。

因为模型中含有曲率的曲面，所以网格划分的总体尺寸控制采用曲率尺寸函数Curvature，并且经过检测网格质量在Element Quality规则下处在好水平范围内。

用Ansys 对上述稳态传热问题进行求解后，可读出热流密度和热传导方向上模型两端的温度，从而计算出模型的热导率；

根据傅里叶稳态热传导规律，通过模型的热流密度q为［11］：

式中：keff为模型的等效热导率；Δz为单元体边长；ΔT为热传导方向上的温差。因而模型的热导率keff为：

因为多数燃料在制作过程中填料颗粒是近似均匀的随机排列在基体中的，为了验证周期排列的适用性，结合MATLAB软件，编程生成随机小球，将包含随机小球的几何图形导入Ansys Workbench中，施加和周期排列情况相同的边界条件，运用同样的热导率算法，计算了随机排列小球的热导率，取多次随机模型的平均值，并和周期排列结果做了比较。

2 结果与讨论

2.1 填料的几何形状对事故容错燃料热导率的影响

为了研究BeO 填料几何形状对事故容错燃料导热性能的影响，本文分别选取了球体、正方体、不同长径比的圆柱体，以及与圆柱体长度相等、两端面为正方形的长方体作为填料分别分布在尺寸为100 μm×100 μm×100 μm的基体中，并且根据填料在UO2基体中的体积分数为5%分别算出球状填料的半径、正方体的边长及不同长径比圆柱体的直径和长度，再利用Ansys Workbench软件模拟稳态传热过程。初始条件：顶面和底面施加相应的温度，单元体四周绝热。参考中国科学院上海应用物理研究所熔盐堆运行温度大概是924.15 K，计算了该温度时材料的热导率。

表1给出了BeO颗粒占UO2基体中的体积分数为5%时，事故容错燃料在常温300 K时热导率随填料形状的变化，其中D:L为圆柱体直径与长度的比。从表1可以看出，填料的形状对热导率有显著影响。其中圆柱体填料长径比不同时，热导率也不同。圆柱体1直径为100 μm，及和基体单元边长相同，圆柱体2～8，圆柱体直径逐渐减小，长度逐渐增加，到圆柱体9，直径最小，长度最大，为100 μm。在这个过程中，热导率先下降后增加，与文献［11］结论稍有不同，是文献［8］的补充。圆柱体1 和圆柱体9 两种极限情况，热导率都比球体、正方体及和与圆柱体长度相等的长方体要大，所以事故容错燃料的BeO填料颗粒，建议选用直径和长度比大于等于3 或者接近1/3.96的圆柱体。

2.2 圆柱体BeO填料纤维的空间取向和热导率的关系

为了验证圆柱体BeO 填料纤维的空间取向和热导率的关系，分别计算了§2.1 中圆柱体1、3、4、5、6、9在温度为300 K、BeO填料颗粒旋转0°、30°、45°、60°、80°、90°（以圆柱轴的方向垂直于温度加载方向为旋转起始点，旋转到平行于温度加载方向时，为旋转90°）时的热导率，结果见图1。

由图1 可以看出，当圆柱体直径与长度的比为1.5:1 时，旋转角度几乎不影响（如图1 中圆柱4），但对于直径与长度的比值大于1.5:1的圆柱体（圆柱体1、3），起始点热导率最高，随着旋转角度的变大，热导率逐渐减小，当轴向与温度加载方向（z轴）一致时，热导率最低。而对于直径与长度的比值小于1.5:1的圆柱体（圆柱体5、6、9），情况恰好相反：随着旋转角度的增大，热导率逐渐变大，当轴向与温度加载方向（z轴）一致时，热导率最大，导热性能最好。

综合表1和图1可以看出，当圆柱体轴长和基体单元边长相等时，及D:L=1:3.96，并且轴的方向和温度加载方向一致时（图2（d）），热导率最大。

目前工业生产的纤维填料在基体中往往是随机取向的，由模拟值发现纤维取向对体系的导热性能影响显著。因此为了追求良好的导热性能，制造过程中就应该使纤维的直径小于长度，并且轴向取向与热流传导方向一致或者夹角尽量小。

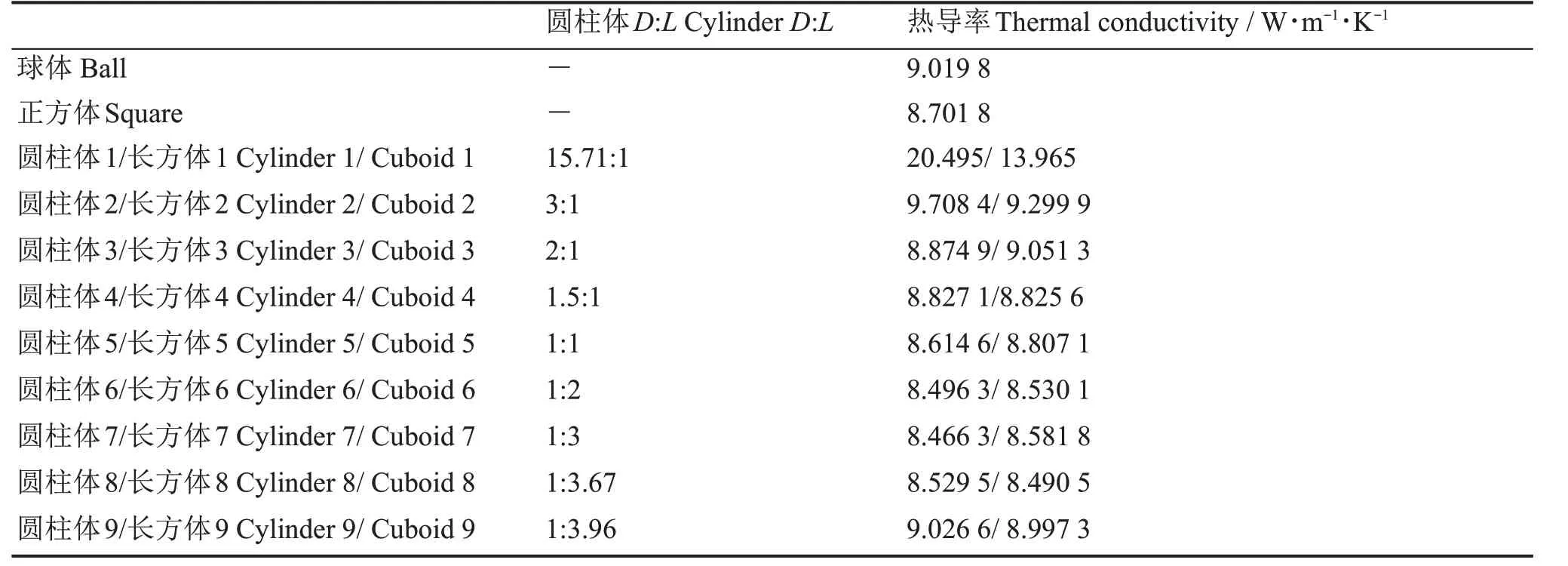
表1 300 K时ATF的热导率随填料颗粒形状的变化Table 1 The thermal conductivity of the ATF with different shape of packing at 300 K

2.3 球体BeO填料颗粒的排列方式和体积大小对热导率的影响

2.3.1 BeO填料颗粒的排列方式对热导率的影响

我们分别采用了MATLAB、COMSOL 软件和Ansys Workbench 相结合的随机排列方式和单独使用Ansys Workbench的规则排列方式，随机排列方式的边长为50 μm，包覆颗粒体积占比为4.8%，共有30个球，半径为3.63 μm，见图2（a）；规则排列的方法是：1）确定一个基本的栅元；2）用该栅元按照一定的方式填充给定的体积。常用到的基本几何栅元可以是简单立方体栅元（Simple Cubic lattice，SC）、体立方体栅元（Body Centred Cubic lattice，BCC）、面立方体栅元（Face Centred Cubic lattice，FCC）（表2）。本文选取的基本栅元中球的半径和和随机排列模型的相同，为3.63 μm，包覆颗粒体积占比为4.8%。三种填充方式的有限元模型见图2（b～d）。图3给出不同堆积方式下的热导率值随温度的变化。

由图3可见，填充体积份额相同时，在常温300～1 100 K 的范围内，无论是随机排列，还是三种周期排列，等效热导率的值都非常接近。因此，排列方式对等效热导率的影响可以忽略。

图1 热导率随圆柱体BeO填料颗粒旋转角度的变化（右边为左边方框处的放大图）Fig.1 Changes of thermal conductivity with the rotation angle of cylindrical BeO packing particles(the picture on the right is an enlarged one of which on the left)

表2 基本栅元的特性和栅元内球数Table 2 Characteristics of basic lattice and number of balls

图2 三种填充方式的有限元模型 (a)随机排列，(b)SC排列，(c)BCC排列，(d)FCC排列Fig.2 Three different filling formats of finite element model

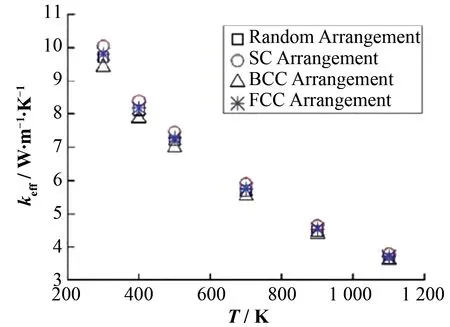
图3 300～1 100 K下填料堆积方式对事故容错燃料热导率的影响Fig.3 Influence of packing stacking mode on thermal conductivity of ATF(for 300～1 100 K)

2.3.2 BeO填料颗粒的大小对热导率的影响

为了研究BeO 填料颗粒的体积大小对热导率的影响，必须考虑接触热阻和界面热阻的影响。

接触热阻是由于接触表面的粗糙度，使有效接触面积小于表面重叠面积。对于尺寸为几微米的颗粒，接触颗粒-颗粒表面的表面粗糙度无关紧要，对于颗粒-基体接触，我们可以假设聚合物基体与颗粒完全接触。因此，接触热阻很小，可以忽略不计。另一方面，界面热阻是由于粒子和基体的性质不匹配造成的。粒子和基体由不同的材料制成，具有不同的密度、德拜温度、频率和声速，在它们之间的边界处为声子流动提供阻力。由于我们在基体中有数千个粒子，这种阻力对声子的流动非常重要，从而降低了复合材料的有效导热系数。

如果粒子比较大，界面热阻的影响可以忽略。有时实际上需要在基体中加入更小的粒子，因为当颗粒越小，界面越致密，界面热阻越大。因此，对于固定的界面热阻，有一个临界直径，用d0表示。当颗粒直径大于d0时，颗粒能提高复合材料的导热系数，反之则会降低复合材料的导热系数。所以，需要对颗粒填充复合材料界面热阻的影响进行分析。

界面热阻RIF，又叫Kapitza 热阻，计算方程如下［16］：式中：ρ 为材料密度；ϑ为声子速度；下标p 和m 分别代表颗粒与基体；Cm为基体等压热容。

本文分别计算了低体积分数（BeO 填料颗粒体积分数分别为5%的SC、FCC 模型）和高体积分数（BeO 填料颗粒体积分数为52%的SC 模型和74%FCC 模型）的球形BeO 填料颗粒复合材料，结果如图4所示，有效热导率keff首先随着R而显著增加，然后达到饱和，达到饱和的点随BeO填料颗粒体积分数而增大，即对于颗粒体积分数为5%的复合材料来说，当颗粒直径为100 μm时，达到饱和，再增大直径，热导率将保持不变。对于BeO填料颗粒体积分数为52%的模型，达到饱和的点为300 μm，对于BeO 填料颗粒体积为74%的模型，达到饱和的点为1 000 μm。图4中黑色直线为基体UO2的热导率，与其他4 条线的交点分别为51 nm、51 nm、50.3 nm、50.3 nm，即BeO 填料颗粒体积分数分别为5%的SC、FCC 模型，d0值均为51 nm；体积分数为52%的SC模型和74%FCC模型，d0值均为50.3 nm，两组数值的偏差为1.4%，由此可知BeO填料颗粒体积分数对d0值的影响可以忽略不计。当颗粒直径小于临界点d0值时，复合材料的keff低于基体热导率，在d0到饱和点的范围内，随着球半径的增加，keff显著增加，当球半径大于饱和点后，keff不再增加。

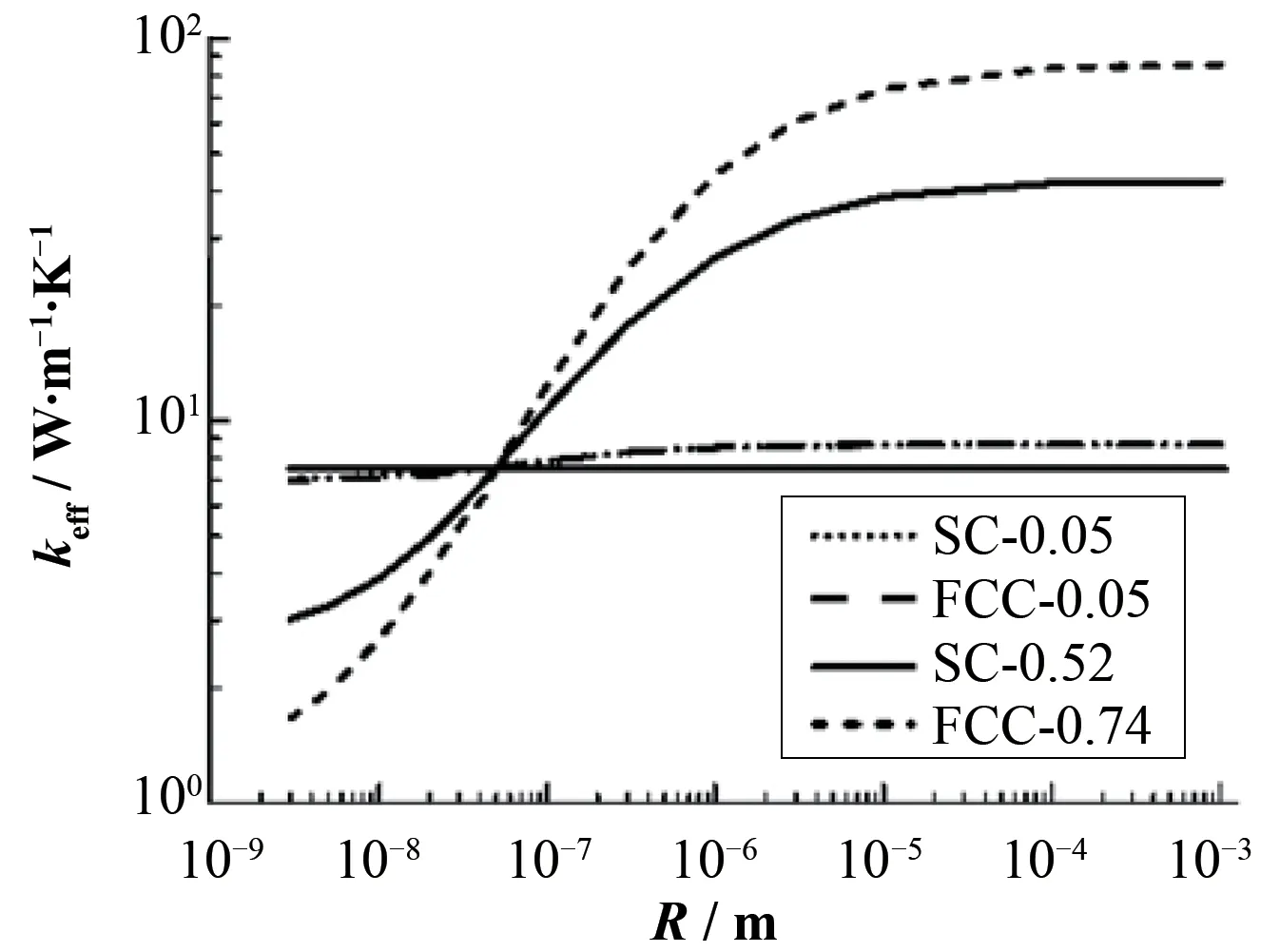
图4 复合材料热导率随球形填充颗粒半径的变化Fig.4 The effective thermal conductivity of composites as a function of the radius of spherical filling particles

2.3.3 与理论值的比较

关于颗粒复合材料的等效热导率的公式，前人做了大量的工作，Verma［17］、Maxwell［18］、Babanov［19］、Brailsford［20］、Singh［21］等给出的结果分别如下，其中ϑ为颗粒的体积百分比含量：

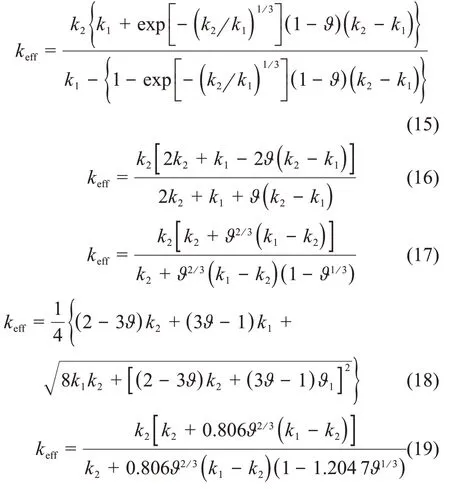
通过式（15）～（19）计算不同颗粒体积含量和热导率情况下的等效热导率的理论值，并和有限元的计算值进行比较。图5 为颗粒体积含量不同时，等效热导率的理论值和计算值的结果对比。从图5可以看出，当颗粒体积含量较小时，各理论值和计算值的差值相对较小，随着体积份额的增大，5个理论公式值之间的差距越来越大，其中Babanov、Singh 与计算值的偏差都在20%以上，Brailsford 在ϑ＞20%以后，偏差也大于20%。Verma、Maxwell 在ϑ≤45%时和计算值比较接近，但是大于45%时这两个公式也不适用了。结果表明：高填充体积分数BeO的有效导热系数对填充量的变化非常敏感。即使是少量的额外填料，热导率的提高也是显著的。为了得到更适合颗粒体积含量较大时的公式，对本工作的有限元法（Finite Element Method，FEM）计算结果进行了拟合，得到了UO2基、BeO为填料颗粒的复合材料的等效热导率公式如下：

3 结语

本文在借鉴了国内外对事故容错燃料的设计和导热性能研究的基础上，针对不同的结构设计方案进行了分析比较。具体得出以下几个方面的结论：

1）事故容错燃料的BeO 填料颗粒，建议选用直径和长度的比大于等于3或者接近1/3.96的圆柱体。

图5 半径相同时等效热导率与体积分数的关系Fig.5 Relationship between equivalent thermal conductivity and volume fraction with the same radius

2）当圆柱体BeO 填料颗粒D:L=1.5 时，方向对热导率几乎无影响；当D:L 大于1.5 时，轴的方向与温度加载方向夹角越大，热导率越高，当垂直于温度加载方向时，热导率最大；当D:L小于1.5时，轴的方向与温度加载方向夹角越小，热导率越高，当平行于温度加载方向时，热导率最大。

3）有效热导率keff首先随着颗粒直径R而显著增加，然后达到饱和。当颗粒直径小于临界点d0值时，复合材料的热导率低于基体热导率；在d0到饱和点的范围内，随着球半径的增加，热导率显著增加；当到达饱和点后，随着BeO 填料颗粒半径的增加，复合材料热导率将保持不变。

4）Verma、Maxwell给出的经验公式在ϑ≤45%时和计算值比较接近，但是大于45%时这两个公式也不适用了。本文给出了UO2基、BeO 为填料颗粒的复合材料在ϑ 大于45%时依然适用的等效热导率公式。