屏蔽材料γ射线积累因子的MCNP模拟

杨体波 王 敏 范新洋 廖光辉 代光明

（成都理工大学核技术与自动化工程学院 成都610059）

随着核事业的发展，关于核的运用越来越广泛，对于γ 射线的屏蔽至关重要，尤其是在放射性比较强的地方，比如核电厂周边以及核废物处置基地。在进行屏蔽设计时需要考虑到“辐射防护最优化”［1］的原则，在相同屏蔽的效果下选择最佳的屏蔽材料，节约成本，达到最优化的目的。

积累因子（B）表示在通过介质的辐射中，某点的总辐射量与没有经过碰撞到达该点的辐射量的比值［2］。在实际的屏蔽设计中，积累因子是一个重要参数，尤其是对于高能γ射线以及高原子序数（Z）屏蔽材料［3］，选择可靠的积累因子可以使屏蔽效果达到最佳。目前使用的屏蔽材料积累因子参考标准是20 世纪70 年代由中国科学院工程力学研究所编纂的《γ射线屏蔽参数手册》［4］。由于数据比较陈旧，在某些情况下并不准确，在后来的发展中，使用MCNP（Monte Carlo N Particle Transport Code）程序对积累因子的模拟计算比较常见。赵峰等［5］用MCNP模拟了不同能量的γ射线、不同源的尺寸、不同辐射角以及不同屏蔽厚度对积累因子的影响；李华等［6］计算了圆柱体介质尺寸对水中γ 射线积累因子的影响；刘珉强［7］针对单层材料研究了轫致辐射对积累因子的影响；Akman 等［8］通过实验得到了几种环境友好型材料的辐射屏蔽参数，并与WinXCom 软件得出的数据进行对比，结果表明有效原子序数Zeff与γ 射线的能量有关，质量吸收系数μ/ρ、辐射屏蔽效率RPE 随γ 射线能量的增加而减小；Mahmoud 等［9］运用MCNP模拟了掺杂CdO硼酸锂玻璃的屏蔽性能，发现随着CdO 含量的增加，其积累因子变小，屏蔽性能得到提高；Tekin等［10］成功制备了不同配比的十二烷基磷酸钠水合物聚合物复合材料，并且计算了材料的屏蔽性能，包括：质量吸收系数、有效原子系数、半值层、积累因子等。在计算屏蔽材料厚度时，积累因子作为一个修正系数对计算的结果具有一定的影响，然而轫致辐射对积累因子具有一定的贡献，所以为了得到准确的积累因子、增加屏蔽材料厚度计算的可靠性，就需要考虑到轫致辐射对积累因子的影响。本文在此基础上，用MCNP 模拟了单层材料、组合材料在不同能量和不同屏蔽厚度下的积累因子，计算了轫致辐射对积累因子的贡献。

1 原理方法与模型建立

1.1 原理方法

γ射线与物质发生作用的主要方式有光电效应、康普顿散射、电子对效应［11］。这三种过程都伴随着次级电子的产生，次级电子又会与物质中的原子发生电离和激发作用，其作用方式又分为次级电子与核外电子的非弹性碰撞、次级电子与原子核的弹性和非弹性碰撞。其中次级电子与原子核的非弹性碰撞又称为轫致辐射。γ射线的吸收分为两种情况，当不考虑康普顿散射效应时，其吸收公式［12-15］如式（1）所示：

如果考虑康普顿散射效应，此时γ 射线的吸收公式为：

式中：I为γ射线出射强度；I0为γ射线入射强度；x为屏蔽材料的厚度，cm；B为积累因子；μ为屏蔽材料的线性吸收系数，cm-1。其中，积累因子的大小与辐射源的几何形状、γ射线的能量、屏蔽材料的性质、屏蔽层的厚度和几何条件等有关［4］。由式（2）可以得到式（3）：

其中：线性衰减系数μ可以由式（4）求出，

式中：ρ为屏蔽材料的密度，g·cm-3；μm为屏蔽材料的质量衰减系数，cm2·g-1，计算时采用MCNP数据库得到的数据。

在利用MCNP 模拟不同能量下屏蔽材料的积累因子时，根据式（3）可知，只需要在材料卡中把屏蔽材料厚度设置为1 个平均自由程（使辐射源的通量减弱e 倍的吸收体厚度（x）被称为平均自由程，Mean Free Path，MFP），改变其能量，通过入射面的γ射线通量和出射面的γ 射线通量即可求出积累因子B。

在模拟不同厚度下的积累因子时，以MFP为单位。平均自由程与线性衰减系数（μ）的关系如式（5）所示：

1.2 模型建立

用MCNP 构建的几何模型如图1 所示，各向同性的点源位于几何中心位置（0，0，0），其发出的γ射线与材料1和材料2发生作用后在球面S2上通过F2卡进行γ 射线通量计数，运用Phys 卡在粒子运输的过程中考虑到轫致辐射，并通过DE卡和DF卡将F2卡的计数转换为对应的剂量，转换系数参考ICRP-21（国际辐射防护委员会21 号出版物）［16］提供的数据，使用的光子截面库为MCPLIBO4。根据积累因子的定义对积累因子进行计算，得到单层材料与多层组合材料的积累因子，分析轫致辐射对屏蔽材料积累因子的影响。

图1 MCNP中建立的几何模型Fig.1 The geometric model established in MCNP

2 单层材料的积累因子模拟

2.1 不同γ射线能量下单层材料的积累因子模拟

将输入文件中的材料1 和材料2 设置为同一种物质（Pb），其厚度（x1+ x2）设置为一个自由程（1 MFP），γ 射线的能量分别为0.5 MeV、1 MeV、2 MeV、3 MeV、4 MeV、6 MeV、8 MeV、10 MeV。对于各向同性的点源，在有无轫致辐射时分别对其积累因子进行模拟。在不考虑轫致辐射时，理论计算的积累因子可以参考文献［17］中给出的数据；在考虑轫致辐射时，理论计算的积累因子可以根据式（6）［18］得出；有无轫致辐射时模拟结果以及理论计算结果，通过拟合得到图2。

式中：X表示屏蔽材料的厚度，单位为MFP；φ(E，X)表示距离点源X 处能量为E 的γ 射线通量密度；B(E，X)表示屏蔽材料的积累因子；∑(E0)表示屏蔽材料对能量为E0的γ光子的能量吸收截面。

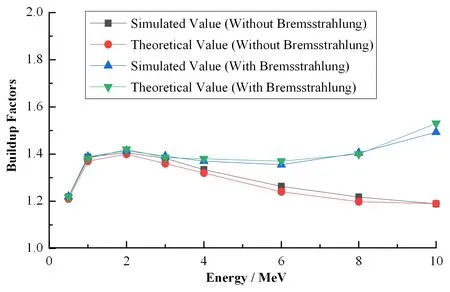
图2 MCNP模拟得到的积累因子与理论计算的积累因子对比Fig.2 Comparison of buildup factors obtained by MCNP simulation and that calculated by theory

从图2 可以看出，MCNP 模拟结果与理论计算的数据符合较好，最大误差不超过5%，证明了模型的可靠性。

根据有无轫致辐射时模拟以及理论计算的，可得出的轫致辐射对积累因子的贡献比例，其计算方式如式（7）所示：

式中：C 为贡献比例；Bw有轫致辐射时的积累因子；Bwo没有轫致辐射时的积累因子。将得到的轫致辐射对积累因子的贡献值用直方图表示，结果如图3。

图3 在不同能量的γ射线下轫致辐射对积累因子的贡献Fig.3 Contribution of bremsstrahlung to buildup factors under different energies of γ ray

从图3可以看出，随着能量的增加，轫致辐射对积累因子的贡献值增大，所以对于高能γ 射线的屏蔽设计时，准确的积累因子是提高屏蔽性能的重要因素。

2.2 不同屏蔽厚度下单层材料的积累因子模拟

设置γ 射线的能量为10 MeV，分别模拟屏蔽材料（Pb）厚度为1～10 MFP 时的积累因子。其模拟结果如图4所示。由图4可以看出，随着屏蔽材料厚度的增加：1）轫致辐射对积累因子的贡献逐渐增大；2）积累因子呈现出上升的趋势；3）考虑轫致辐射时的积累因子增加幅度大于不考虑轫致辐射时的积累因子。

图4 积累因子与屏蔽材料厚度的关系Fig.4 Relationship between buildup factors and thicknesses of shielding materials

3 组合材料的积累因子模拟

分别模拟了前层为低Z 材料、后层为高Z 材料以及前层为高Z 材料、后层为低Z 材料时的积累因子。在不同γ 射线能量（0.5 MeV、1 MeV、2 MeV、3 MeV、4 MeV、6 MeV、8 MeV、10 MeV）下模拟积累因子时，其组合设计为1 MFP Al+1 MFP Pb、1 MFP Pb+1 MFP Al；并且模拟了不同屏蔽厚度时（1～10 MFP）的积累因子。

3.1 不同γ射线能量下组合材料的积累因子模拟

将屏蔽材料设置为1 MFP Pb+1 MFP Al 的组合，能量分别为（0.5～10 MeV），模拟的积累因子结果如图5所示。

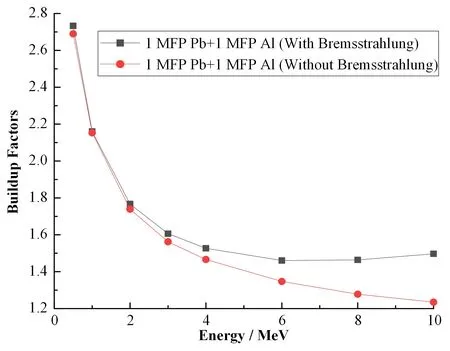
图5 前层为Pb、后层为Al时的积累因子Fig.5 Buildup factors of Pb in the front layer and Al in the back layer

从图5 中可以看出，在高Z 材料+低Z 材料的组合方式下，其积累因子随着能量的增加而减小，并且轫致辐射对积累因子的影响逐渐增加，与单一材料的积累因子随能量的变化趋势相似。这是由于γ射线能量变大后，在保持屏蔽材料厚度不变的情况下，没有经过碰撞到达出射面的γ 射线通量增加，使得出射面的射线总通量与其比值变小，即积累因子变小。

将屏蔽材料设置为1 MFP Al+1 MFP Pb 的组合，能量分别为（0.5～10 MeV）。将模拟得到的轫致辐射对单层材料积累因子的贡献与轫致辐射对组合材料积累因子的贡献做对比得到图6。

图6 轫致辐射对单层材料和组合材料积累因子的贡献对比Fig.6 Bremsstrahlung contribution to buildup factors of monolayer and composite materials

由图6 可知，随着γ 射线能量的增加，轫致辐射对单层材料和组合材料积累因子的贡献都呈现出增加的趋势；在低能的时候轫致辐射对前层为高Z 材料、后层为低Z 材料积累因子的贡献大于对前层为低Z 材料、后层为高Z 材料积累因子的贡献和对单层材料积累因子的贡献；在高能的时候轫致辐射对单层材料积累因子的贡献和对前层为低Z 材料、后层为高Z材料积累因子的贡献相差不大。

3.2 不同屏蔽厚度下组合材料的积累因子模拟

在模拟不同厚度的组合材料积累因子时，γ射线的能量设置为10 MeV，组合方式为Al+Pb，厚度分别为1 cm+1 cm、2 cm+2 cm、…、10 cm+10 cm，模拟结果如图7。从图7 可以看出，对于组合材料来说，其积累因子与厚度的关系与单层材料类似，随着屏蔽厚度的增加，积累因子呈现上升的趋势，并且轫致辐射对积累因子的贡献逐渐增加。

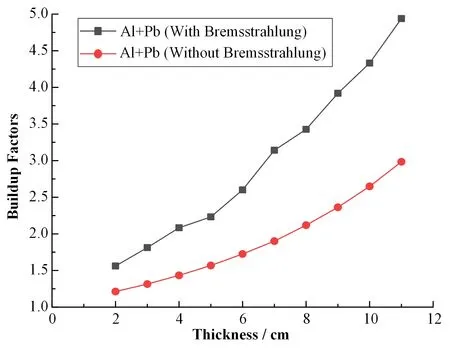
图7 不同屛蔽厚度时组合材料的积累因子Fig.7 Buildup factors of composite materials with different thicknesses

4 结语

利用MCNP软件模拟了不同γ射线能量以及不同屏蔽厚度时单层材料和组合材料的积累因子，并计算了轫致辐射对积累因子的贡献，得出以下结论：

1）对于单层和组合材料，积累因子随着γ 射线能量的增大呈现出减小的趋势，且组合材料的下降趋势更明显。

2）对于单层和组合材料，积累因子随着屏蔽厚度的增加而增大。

3）轫致辐射对积累因子的贡献在低能时较低，在高能时较大，并且对于单层材料和组合材料的贡献相差不大。

4）随着屏蔽厚度的增加，轫致辐射对积累因子的贡献逐渐增加，对于组合材料来说，其积累因子增加的趋势略大于单层材料。

在屏蔽高能γ 射线时，轫致辐射对积累因子的影响不可忽略。一些工作在高放射性环境下的电子器件，由于其封装材料要求不导电，可以选用不导电材料作为内层，屏蔽性能较好的金属作为外层的组合方式进行屏蔽；对于工作在复杂环境下的机械（如核救灾机器人），则要求具有较强的灵活性，在保证屏蔽效果的前提下，可以考虑密度大与密度小的材料进行组合的方式，本文的工作则可以为其屏蔽设计提供了一些参考。