基于线性回归和MLP神经网络的招标采购预测模型

庞铖铖，戎袁杰，刘昕，宋梦昕，王光旸

(国网物资有限公司，北京市 100120)

招标采购过程中，中标价格往往是招标人比较关注的结果，中标价格的高低对于招标人的预算管控、项目经营收益都存在着很大的影响。对于国家电网公司集中规模招标采购，采购频次高，规律性较强，为了准确管控预算以及提升公司经营管理水平，利用集中规模招标历史数据，提出两种预测模型，即线性回归模型和多层感知器[1](multi-layer perceptron，MLP)神经网络模型，对招标采购项目的中标价格进行预测。

线性回归的原理是通过含有自变量和因变量的线性等式来模拟两个变量之间的关系，再将作为自变量和因变量的现有数据代入该线性等式，利用最小二乘法得到系数后，即可针对新的自变量预测因变量的变化趋势。MLP神经网络是典型的前馈神经网络，该模型可以模拟人脑神经元存储或学习大量输入和输出数据的行为，同时无需用变量描述映射关系，直接使用输入和输出数据构造模型，尤其对非线性关系具有较强的模拟能力。

本文以某种受原材料价格影响较大的变电设备为例，通过线性回归和MLP神经网络两种方式，以实际数据为基础对该变电设备报价进行预估，并对比不同方式预估价格的准确性。

1 线性回归模型

简单线性回归分析是基于给定的单个解释变量的回归分析，用于研究单个因变量Y和单个自变量X之间的线性关系，线性回归模型的一般形式为

Y=a+bX+ε

式中：a—常数项；

b—回归系数；

ε—随机误差，即随机因素对因变量所产生的影响。

采用最小二乘法得到模型参数估计值。

在得到线性等式后，还应采用统计检验来验证该模型的正确性以及参数估计值的可信程度，通常使用的统计检验方法包括拟合优度检验、线性显著性检验、变量显著性检验，以及参数置信区间估计[2]。

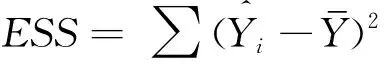
(2)方程总体线性的显著性检验(F检验)，设定原假设H0∶R=0(线性不显著)，其他假设Ha∶R≠0(线性显著)，统计量F=[ESS/k]/[RSS/(n-k-1)]服从自由度为(k,n-k-1)的F分布。给定显著性水平a(一般取0.05或0.1，即置信度为95%或90%)，查表得到临界值Fa(k,n-k-1)，根据训练样本得出F的数值，通过F>Fa(k,n-k-1)来拒绝原假设H0(线性不显著)，以判定原方程总体上的线性关系显著成立。

2 MLP神经网络模型

神经网络旨在模拟神经系统构造与功能进行数据处理，不断调整模拟神经元之间的链条的权值，以使得整个网络可以较好拟合训练数据的关系。多层感知器是一种基于神经网络的算法模型，其基本结构包括输入层、隐含层以及输出层，如图1所示。每个输入节点都通过一个加权的链连接到输出节点，该加权的链用以模拟神经元之间的连接强度，训练一个多层感知器就是不断调整加权链的权值的过程，直至能较好地拟合训练数据的输入输出关系为止[3]。

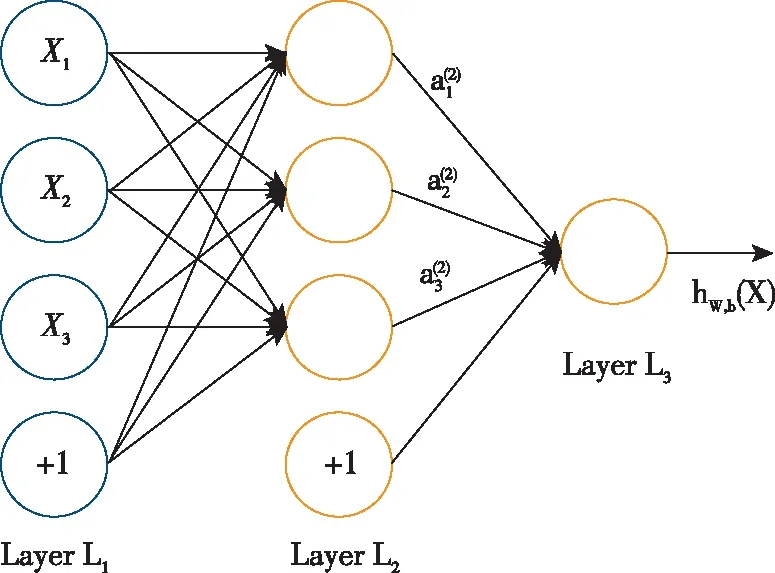
图1 MLP神经网络基本结构

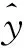
图2 双曲正切激活函数

多层感知器需通过不断调整权值参数w来完成学习过程，直至输出和训练样本的实际输出一致，权值调整公式为

(1)

式中：wk—第k次循环后第i个输入后链接的权值;

β—学习效率；

xij—训练样本xi的第j个属性值。

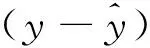
3 算例对比分析

以某变电设备产品为例，选取2010—2019年各采购批次原材料价格和变电设备中标价格作为训练样本，原材料价格作为自变量，变电设备价格作为因变量；同时选取两种电压等级产品作为研究对象，分别记为典型产品1和典型产品2，将同时利用线性回归分析和MLP神经网络模型对两种典型产品进行预测。

3.1 简单线性回归模型

3.1.1 绘制散点图

首先利用SPSS软件将两个变量的样本数据作出散点图，如图3—图4所示。从图像层面上对两个变量之间是否具有线性相关关系进行判断，再进一步进行相关性分析。

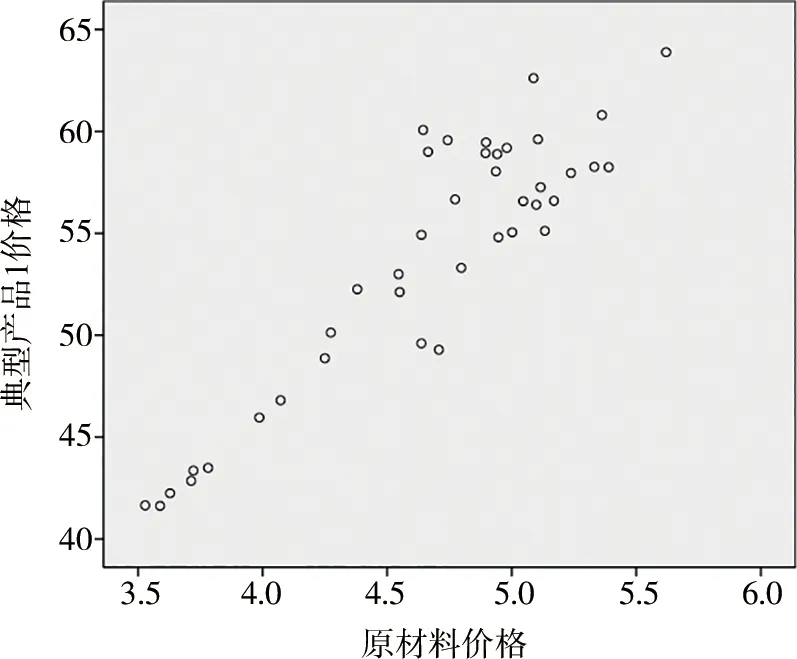
图3 典型产品1价格与原材料价格关系散点

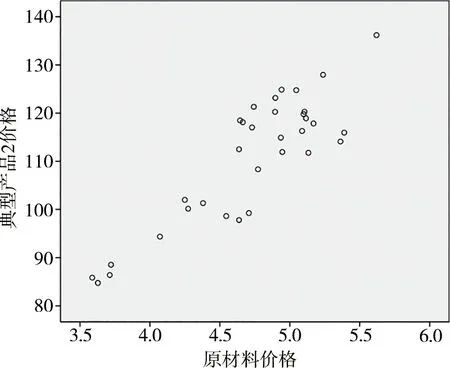
图4 典型产品2价格与原材料价格关系散点

由图3、图4可以看出，两个变量之间存在明显的线性正相关关系，因变量随自变量的增大而相应增大。相关系数是测定因变量和自变量之间相关关系程度及方向的指标[4]，计算公式为

(2)

相关系数越接近于1，相关性越强，反之则相关性越弱。计算典型产品价格和原材料价格的相关系数，得到结果如表1所示。对于两种典型产品，其中标价格和原材料价格两个变量之间的相关系数均超过0.8，呈高度正相关。

表1 变电设备价格和原材料价格的相关系数

3.1.2 建立回归模型

利用SPSS软件对训练样本数据进行回归分析，采用最小二乘法建立模型参数的估计，根据输出结果得到典型产品价格回归模型。

典型产品1价格模型：

Y1=4.136 8X1+5.453 4

典型产品2价格模型：

Y2=8.933 6X2+5.356 5

3.1.3 模型检验

对上述线性回归模型进行统计检验，选择F检验与t检验。

表2 模型汇总

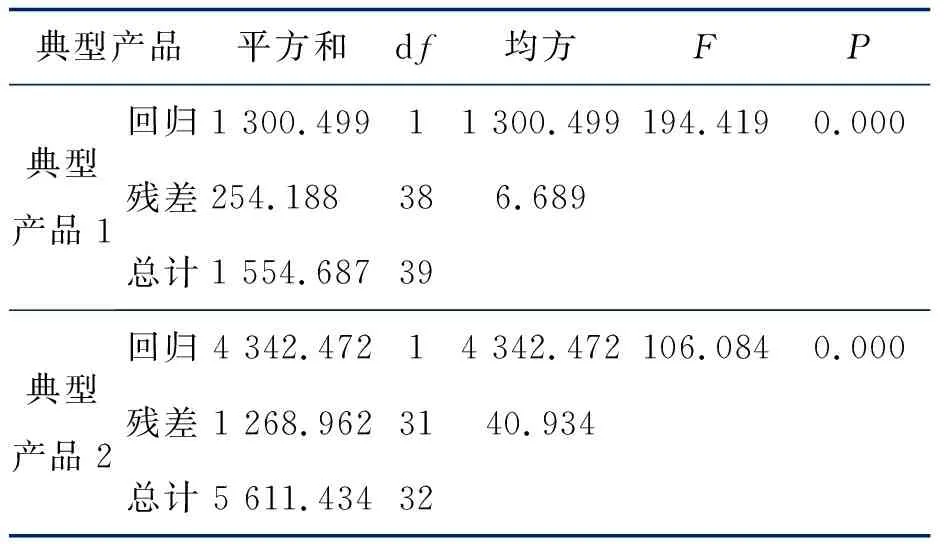
表3 Anovab

首先做拟合优度检验。表2数据显示，从拟合优度来看，典型产品1价格模型：R=0.915，R2=0.837；典型产品2价格模型：R=0.880，R2=0.774。表明对于典型产品1，因变量总体变动量的83.7%可以被对应的线性方程解释；对于典型产品2，因变量总体变动量的77.4%可以被对应的线性方程解释。

接下来做方程总体线性的显著性检验(F检验)。根据表3数据显示，模型能够较好地解释总变动量。两种研究对象的预测模型F检验量的P值趋近于0，小于0.01，故应拒绝线性不显著的原假设，说明两种变量之间存在显著的线性关系。

最后做变量的显著性检验(t检验)。通过t值计算式，可以得到两种典型产品预测模型的t值分别为14.14和11.40。查询t值表，发现t均落入拒绝域，故拒绝原假设H0，可得到R显著的结论，说明自变量能够显著地解释因变量。

3.2 MLP神经网络模型

本文使用SPSS软件对MLP神经网络建模，分析过程主要分为分区数据集、训练模型和预测结果三个步骤。

3.2.1 分区数据集

将活动数据集划分为训练集、测试集和验证集三个集合，训练集合中的数据用于训练神经网络，测试集合中的数据用来监视训练过程中的错误以防过度训练，而验证集合中的数据则用于评估训练所得到的神经网络的准确性。该案例中，训练、测试和验证样本指定7、3、0，即按70%、30%和0%的比例来划分样本，再将样本数据随机分配到三种样本集合中。

3.2.2 训练模型

在满足精度要求的前提下，为了提高数据训练效率，在该神经网络的体系结构中构建一个使用双曲正切激活函数的隐藏层，并选择批处理的训练方式，即运用训练数据集中的所有记录信息，以使得总误差最小化。由于该方法在满足任何结束训练的条件前都需要不断调整权重，所以存在将数据传递数次的可能性。优化算法在调整后选择了相应的共轭梯度，模型参数如图5—图6所示。两种典型产品的平方和误差为2.607%和2.952%，相对误差分别为0.168%和0.236%。

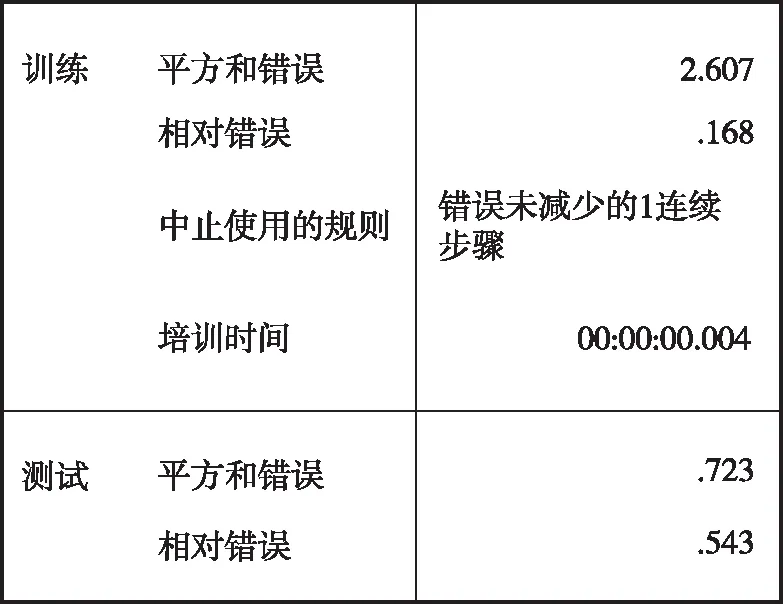
图5 典型产品1预测模型汇总

图6 典型产品2预测模型汇总

3.2.3 预测结果

通过训练样本得到满足要求的神经网络模型，预测如图7—图8所示，残差分析如图9—图10所示。

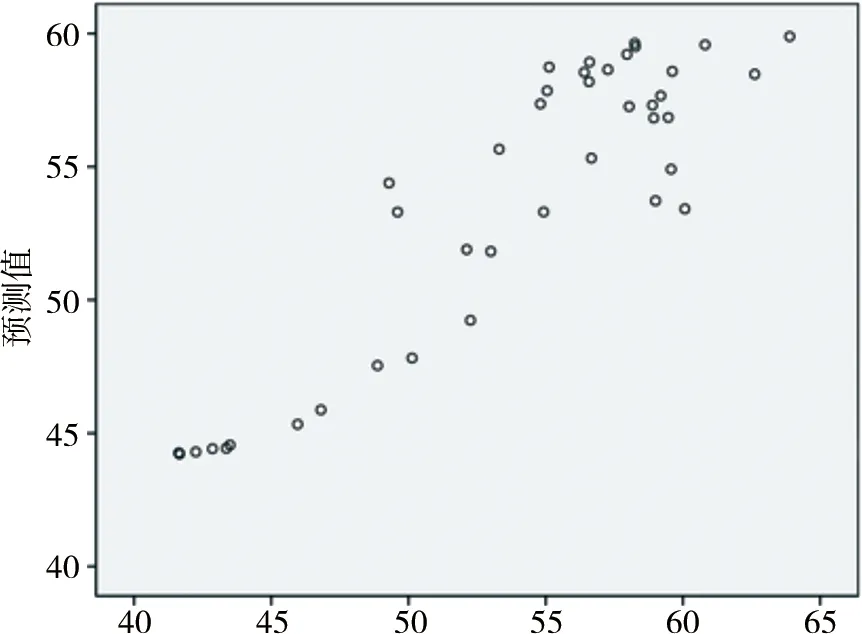
图7 典型产品1模型预测

图8 典型产品2模型预测

图9 典型产品1残差分析

由图9和图10可以看出，典型产品1残差在±5以内，典型产品2残差在±15以内，均在可接受范围内。

4 模型预测效果

本文采用平均相对误差(ARE)和标准误差(SE)两个指标[5]来评价上述两种模型的预测准确性。标准误差(SE)也是描述预测值与实际值之差的一种度量，其值越小，预测精度越高。平均相对误差和标准误差公式分别为式(3)、式(4)：

(3)

(4)

式中：yi—实际值；

n—预测样本数。

通过计算得出具体数值，见表4。

表4 预测误差估计结果

由表4可知，两种预测结果的平均相对误差和标准误差数值均较小，平均相对误差都在5%以内，标准误差在5%左右。此外，由于本文所研究的变电设备，其价格与原材料价格线性关系较为凸显，所以，无论是将平均相对误差还是标准误差作为判断指标，对于两种典型产品，线性回归模型预测精度略优于MLP神经网络，但两模型预测精度差异并不是十分显著。两种方法在进行变电设备价格预测时均有一定的参考价值。

5 结 论

通过SPSS软件，建立线性回归和MLP神经网络两种模型，对某种变电设备招标采购中标价格进行预测。预测结果说明：

(1)两种模型的预估值与真实值的平均相对误差和标准误差都较小，对于投标价格受原材料价格影响较大的变电设备，两种模型都可以对招标采购价格做出较为精准的预测，均具有一定的参考价值。

(2)对于与原材料价格线性关系较为凸显的产品，两种模型的预测能力不相上下，线性回归模型预测精度略优于MLP神经网络模型，但随着训练样本集的增大，MLP神经网络模型的预测能力可能更强。

综上，两种模型在招标采购中变电设备价格预测上并不存在绝对的优劣，模型的预测精度与变电设备的类别有一定相关性。在实际应用中，可以结合线性回归模型和MLP神经网络模型对变电设备价格进行综合判断。