城市有轨电车轮缘承载式辙叉动力学特性研究
司道林 张立军 王树国 杨东升 王璞
(1.中国铁道科学研究院集团有限公司铁道建筑研究所,北京 100081;2.高速铁路轨道技术国家重点实验室,北京 100081;3.铁科(北京)轨道装备技术有限公司,北京 102202)
城市有轨电车起源于19 世纪80 年代,在欧洲有着上百年的运营历史[1]。有轨电车不仅建设成本低、周期短,且具有节能环保、适应性强、灵活度高等特点。发展有轨电车是大、中型城市缓解交通压力的重要举措[2]。
有轨电车运营环境不同于地铁,有其自身特点,不断有学者开展相关研究。文献[3]根据城市规模、交通需求和土地利用规划将有轨电车划分为三种运营模式,阐述了不同模式下有轨电车在城市公共交通中的地位、角色及其适用环境。但有轨电车主要修建在地上,并非所有区段均有专用路权,在特殊区段通常与地面交通工具享有同等的路权,且线路走向受到已有城市格局的限制。因此,其建设场地空间极为有限,为增加线路的灵活性,设计时不得不采用小号码单开道岔、线型特殊的梳子型组合道岔[4],以及两股轨道直接相交的交叉。正线、站场分别采用6 号、3 号道岔,号码均远小于普通铁路道岔[5]。轨道交叉可分为菱形交叉和垂直交叉两种[6]。道岔辙叉与轨道交叉具有类似的结构特征和功能,均为两股钢轨以一定的角度交叉,因此本文将道岔辙叉与轨道交叉统称为辙叉。
辙叉多由槽形钢轨制造[7],典型结构如图1(a)所示。为实现辙叉区的特定功能,需设置一定宽度的轮缘槽,以便车轮轮缘顺利通过,但这样会导致钢轨顶面中断,荷载需在翼轨与心轨间转换。辙叉角较小时翼轨与心轨共同承载(如图1(b)所示),轮载可由翼轨逐渐过渡至心轨;辙叉角较大时翼轨和心轨无法共同承载(如图1(c)所示),车轮支承被中断,由翼轨直接跳至心轨。这样不仅产生较大轮轨冲击荷载,而且会给行车带来较大安全隐患。
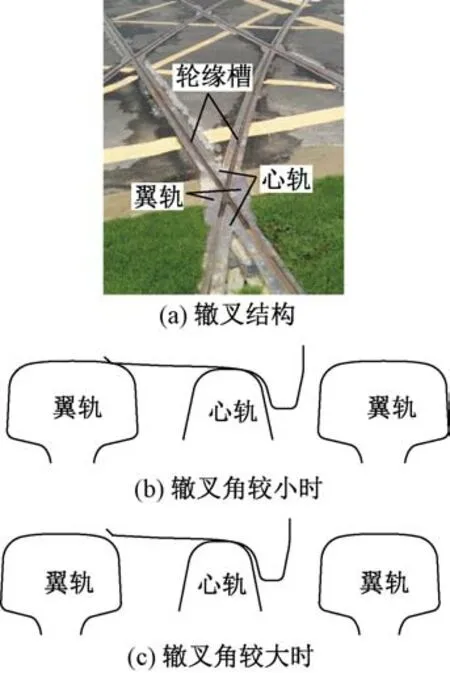
图1 辙叉区轮轨接触几何关系
为使车轮连续支承设计了轮缘承载式辙叉,与传统辙叉明显不同的是车轮以轮缘承载的方式跨越轮缘槽。本文分析轮缘承载式辙叉的工作原理,继而建立有轨电车-轮缘承载式辙叉的动力学模型,分析辙叉结构参数对有轨电车轮轨动力学响应的影响规律,为确定辙叉区合理通过速度提供理论依据。
1 轮缘承载式辙叉的工作原理
轮缘承载式辙叉与文献[8]提出的固定型立交式辙叉有相通之处。固定型立交式辙叉通过轮缘承载的方式将车轮托起,使轮缘高于轨顶,跨过不间断的主线钢轨。其主要适用于直、侧向运量悬殊的运输环境,达到主线钢轨与区间钢轨同寿命、兼顾侧向行车的目的。
本文介绍的轮缘承载式辙叉与固定型立交式辙叉的功能定位及工作原理有所不同,主要用于辙叉角较大时解决轮载无法平顺过渡的问题。此类辙叉具有深度变化的轮缘槽。通过调整轮缘槽深度,实现轮载在踏面和轮缘间转换,使得车轮顺利通过辙叉。
车轮通过辙叉区时轮轨接触特征如图2所示。车轮驶入辙叉前,轮缘槽深度大于轮缘高度,轮缘顶部不会接触轮缘槽底。临近辙叉时轮缘槽底设置一定坡度,轮缘槽深度不断减小,当轮缘槽深度与轮缘高度相同时轮缘顶部与轮缘槽底接触,轮载由踏面和轮缘顶部共同承担(图2中A 点),轮缘槽深度继续减小,直至将车轮抬起一定高度(图2 中B 点),使车轮踏面脱离钢轨顶面,轮载完全由轮缘承担。待车轮驶过辙叉区后,轮缘槽深度开始增加(图2中C 点),车轮高度下降,使轮载再由轮缘顶部逐渐恢复至踏面(图2中D 点),轮缘顶部与轮缘槽底脱离,轮轨接触几何关系回归常态,至此车轮通过了大角度辙叉。由于轮缘承载区的轮缘槽深度小于常规值,故此类辙叉通常称为浅槽辙叉。
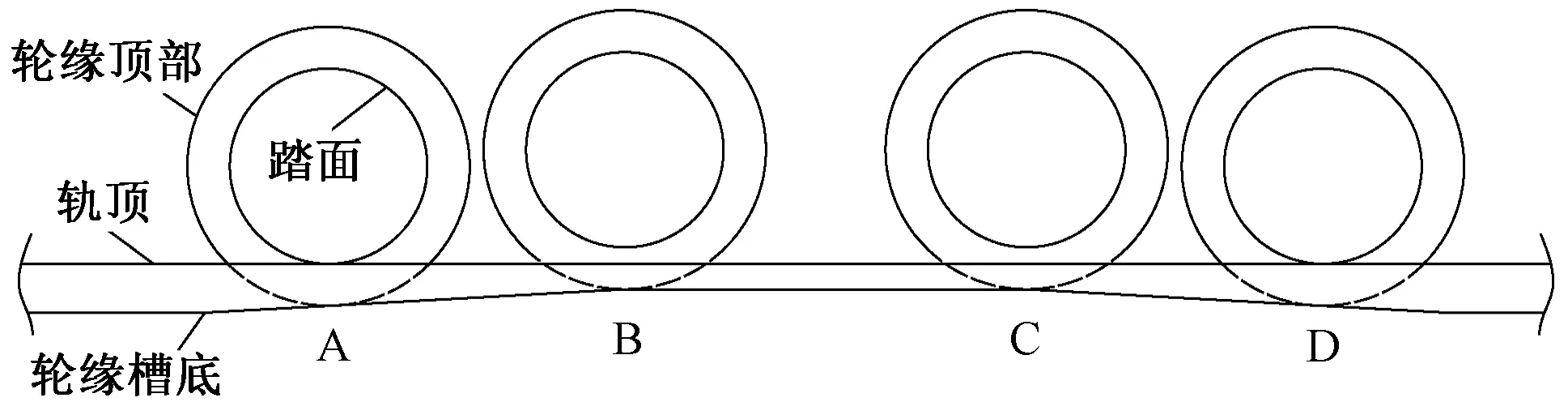
图2 车轮通过辙叉区时轮轨接触特征
车轮以轮缘连续承载的方式通过辙叉,避免了轮载在翼轨与心轨间不连续过渡导致的剧烈轮轨冲击。但此过程中不仅需要轮载在钢轨顶面与轮缘槽底间相互转换,而且需将车轮抬升至一定高度,不可避免地产生轮轨冲击荷载,影响车辆垂向平稳性。因此有必要建立有轨电车-辙叉动力学模型,分析轮缘承载式辙叉的动力学性能。
2 有轨电车轮轨动力学响应数值模拟
2.1 模型的建立和工况的设置
基于多体动力学理论[9],采用NUCARS 软件建立有轨电车-轮缘承载式辙叉的动力学模型。有轨电车由5节车体、3个构架和6条轮对组成,车体、构架和轮对为主要运动部件。第1 节和第5 节为动车,配备有动力转向架;第3 节为拖车,配备无动力转向架;第2节和第4 节为无转向架的浮车,以铰接的方式与前后车体连接,如图3所示。

图3 有轨电车示意
车体与构架、构架与轮对间分别采用二系、一系悬挂连接,车体间通过灵活度较高的铰接装置连接,以实现车体间较大的相对位移和转动。车体质量经二系悬挂传递至构架,再经一系悬挂传递至轮对,浮车荷载通过铰接装置传递至两端相邻车体。各部件间均可独立运动。因此,建立动力学模型时将车体、构架和轮对均视为多自由度刚体,一系、二系悬挂和车间铰接装置的力学特性通过改变弹簧刚度、阻尼参数表征。有轨电车的每节车体和每个构架均有横向位移、垂向位移、侧滚、点头、摇头5 个自由度,每条轮对有横向位移、垂向位移、侧滚、摇头4个自由度。
采用NUCARS 软件中的双轨方法建立道岔模型,双轨由主轨和辅轨构成。主轨用于模拟基本轨,辅轨用于模拟轮缘槽。辅轨可相对主轨横向位移、垂向位移和转动,实现轮缘槽深度的变化。图4 展示了车轮由图2 中A 点向D 点行驶过程中轮轨间3 种典型接触状态:车轮通过D点后到达A点前由主轨承载;车轮到达A 点和D 点时由主轨与辅轨同时承载;车轮到达B点和C点时由辅轨承载。

图4 轮缘槽深度变化时出现的3种典型接触状态
2.2 模拟结果与分析
为使轮缘槽底、轮缘顶部磨损情况下轮缘承载时车轮踏面仍能完全脱离轨顶,轮缘槽深度须比轮缘高度小7 mm,轮缘槽深度变化率取10‰。以此辙叉参数为基准,计算有轨电车以不同速度通过辙叉时轮轨垂向力、轮轨横向力、减载率、脱轨系数和车体加速度,通过分析各项动力学指标随速度的变化规律,得到有轨电车通过辙叉区时的动态响应。
有轨电车以时速25 km 通过辙叉时各项动力学指标变化情况见图5。

图5 有轨电车以时速25 km通过辙叉时动力学指标变化情况
由图5 可知:①轮轨垂向力出现4 次明显波动。第1 次(A 点)波动反映轮缘顶部开始接触轮缘槽,由轮载从踏面转移至轮缘顶部所致;第2 次(B 点)和第3 次(C 点)波动出现在轮缘槽底的变坡点处,由车轮质心高度变化所致;第4 次(D 点)波动反映车轮踏面重新接触轨顶,由轮载从轮缘顶部恢复至踏面所致。轮载在踏面和轮缘间转换过程中轮轨垂向力最大值达到38.5 kN,为静轮载(35.3 kN)的1.1 倍。在轮缘槽底变坡点处轮轨垂向力明显减少,最小值为27.1 kN。减载率达到最大值0.22,小于安全限值。②轮轨垂向力产生波动的同时,还导致轮轨横向力随之波动,轮轨横向力最大值为2.6 kN。脱轨系数最大值为0.07,小于安全限值。③通过辙叉时需将轮对抬升7 mm,因此车体产生大幅度振动。车体出现3 次明显振动,车体垂向加速度最大值达到1.4 m/s2。车体横向加速度未受到明显影响,最大值仅为0.1 m/s2。
由上述分析可见,有轨电车通过轮缘承载式辙叉时主要影响垂向动力学指标,对横向动力学指标影响较小。因此,分析有轨电车行车速度对轮轨动力学响应的影响规律时主要分析垂向动力学指标。
有轨电车行车速度在5~45 km/h 变化时轮轨垂向力、减载率和车体垂向加速度的变化规律见图6。可见:随着行车速度提高,3 项动力学指标表现出不同的变化规律。轮轨垂向力、减载率均呈线性增加,轮轨垂向力由36.2 kN 增至41.7 kN,减载率变化幅度较大,由0.02 增至0.41。减载率最大值小于安全限值。车体垂向加速度明显呈非线性增长。速度超过15 km/h后车体垂向加速度快速增加,当行车速度达到25,35,45 km/h 时车体垂向加速度分别达到1.4,1.6 和2.2 m/s2。可见,提高行车速度不仅显著恶化有轨电车在辙叉区的平稳性,而且在一定程度上增加了安全风险。

图6 动力学指标随有轨电车行车速度的变化规律
参考文献[10]中车体加速度评价准则,正常运营时车体垂向加速度应控制在1.5 m/s2以内。因此,有轨电车通过轮缘承载式辙叉的速度不宜超过15 km/h,站场内对平稳性要求不高时行车速度可适当提高,但不应超过25 km/h。
3 结论
1)有轨电车通过轮缘承载式辙叉时轮载需在踏面和轮缘之间相互转换,此过程中产生的明显轮轨冲击荷载经悬挂传至车体,引发车体大幅度垂向振动。因此有轨电车通过轮缘承载式辙叉时主要影响有轨电车垂向动力学指标,对横向动力指标影响较小。
2)随着行车速度提高,各项垂向动力学指标均明显呈增加趋势,车体垂向加速度的增幅最明显,车体平稳性急剧恶化。日常运营时有轨电车通过轮缘承载式辙叉的速度不宜超过15 km/h,站场内对平稳性要求不高时行车速度可适当提高,但不应超过25 km/h。

