双车道公路弯道回旋线长度对行车特性的影响

（同济大学道路与交通工程教育部重点实验室，上海 201804）

回旋线作为弯道线形的基本构成要素，被广泛应用于各级公路设计中，但世界各国对回旋线的安全性能存在一定的争议。早期研究的焦点为回旋线与交通事故率的关系。Chudworth等［1］指出，在双车道公路上不设回旋线的弯道事故率比设置回旋线的弯道低80%，因此建议道路设计时不再使用回旋线。Tom［2］也提出了类似的观点，在曲率半径大于168 m（550 ft）时，回旋线过渡段的事故率明显高于不设回旋线的弯道。也有学者提出了相反的观点。以Council［3］、Zegeer等［4］为代表的调查报告则分别证明了回旋线的存在显著降低了双车道公路弯道的事故率。到了后期，研究的焦点转移到回旋线的长度对驾驶行为的影响。Karl等［5］实地收集了12个弯道曲中点的运行车速，结果表明回旋线的存在对曲中点85%分位速度没有显著影响。徐进等［6］通过仿真实验证明回旋线长度对弯道车速及行车轨迹均有显著影响，并且回旋线越长，对车速变化的影响越大。林雨等［7］基于驾驶员预瞄点模型进行了Simulink 仿真，指出回旋线参数对侧向偏移量存在影响，并建议回旋线长度取0.4R～0.6R（R为圆曲线半径，m）为宜。Spacek［8］实地测量了车辆在双车道弯道上的侧向偏移量，在半径120～230 m的弯道上，当回旋线参数为0.33R～0.50R时，车辆的轨迹接近最优轨迹。针对回旋线长度，中美两国设计规范也有相应的规定。《A policy on geometric design of highways and streets》（7th edition）建议以1 m 为侧向偏移的上限控制回旋线的最大长度，以横向加速度变化率控制回旋线的最小长度，同时还建议以2 s设计车速行程为最佳回旋线长度［9］。我国的《公路路线设计规范》规定，回旋线参数A的取值应满足R/3≤A≤R，并建议半径接近100 m 时A宜等于R，接近3 000 m 时宜等于R/3［10］。

回旋线长度对驾驶行为的影响主要在于车速和行车轨迹2个方面。过往的研究方法主要是通过实地测量和计算机仿真，存在问题有：①实车实验环境中弯道设计参数千变万化，难以对影响因素加以控制；②实地测量受到环境和设备的制约，往往只能测得有限点的数据，难以描述整个路段的车辆行为特征；③仿真实验是基于动力学模型，与真实的驾驶行为存在偏差；④相比《A policy on geometric design of highways and streets》，《公路路线设计规范》更建议灵活运用回旋线参数设计值，尤其是针对半径为100～3 000 m 的弯道；⑤虽然国内外的研究均指出回旋线长度对行车安全有显著影响，但研究的结论并不统一。因此，有必要在我国规范的框架内，对回旋线的合理长度进行研究。

针对以上问题，采用驾驶模拟实验，以车速和行车轨迹为研究对象，以曲线半径为控制变量研究回旋线长度对车辆行为的影响，为回旋线长度的优化设计提供参考。

1 实验方案

1.1 实验方法及合理性

现实中公路弯道设计参数的选用受到地形条件的约束，曲线的半径和回旋线长度都不尽相同，难以实现对实验条件的控制。驾驶模拟实验则可以根据需要设计道路场景，固定其中的一个或某几个设计参数进行研究，具有安全、可重复实验等优点。针对驾驶模拟实验的合理性，Joris等［11］和Godley等［12］的研究结果指出，驾驶模拟器可用于乡间双车道公路弯道路段的车速研究。Wade 等［13］研究了驾驶模拟器输出的车辆轨迹数据，证明模拟实验的轨迹追踪行为与实际行车相一致，虽然模拟车辆的力反馈与现实中实车驾驶员收到的反馈有所区别，但是结果并不存在显著差异。因此，使用驾驶模拟实验研究双车道公路回旋线段的驾驶行为具备可行性。

1.2 实验仪器

实验基于同济大学ScaNer Studio 驾驶仿真平台（见图1）。该平台可提供沉浸式的仿真环境，可收集包括车速、三轴加速度、相对车道中线偏移量、方向盘转角、油门开合度等在内的数十种数据。本实验设置的采样频率为50 Hz。

图1 驾驶仿真平台Fig.1 Driving simulation platform

1.3 场景设计

实验的研究对象为水平路段的基本型平曲线，采用ScaNer Studio 的Terrain 模块进行三维建模。实验道路为双向两车道，设计车速为40 km·h-1，车道宽度为3.5 m，路拱横坡为2%。实验共有5 个场景，每个场景包含5～8个弯道，相邻的弯道间由一段200 m 的直线相连，同一场景的各圆曲线半径R相同。依据《公路路线设计规范》中的“圆曲线最小半径（一般值）”、“不设超高最小平曲线半径”和《公路项目安全性评价规范》中二、三级公路有关“平曲线路段”的规定，确定半径设计值范围为100～500 m［10，14］。平曲线超高值、加宽值均依照《公路路线设计规范》选取，如表1所示。

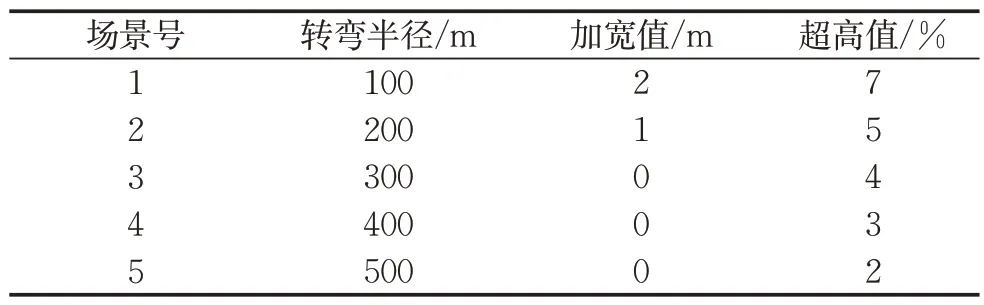
表1 超高加宽设计值Tab.1 Design value of superelevation and widening

沿桩号起点至终点方向，所有的曲线转向均为左转弯。根据《公路路线设计规范》中平曲线最小长度、回旋线最小长度、超高渐变率的相关规定，确定各回旋线参数。每个弯道的第一回旋线、圆曲线和第二回旋线的长度比为1∶1∶1。回旋线参数A及道路转角如表2所示，表中变量C=A/R。

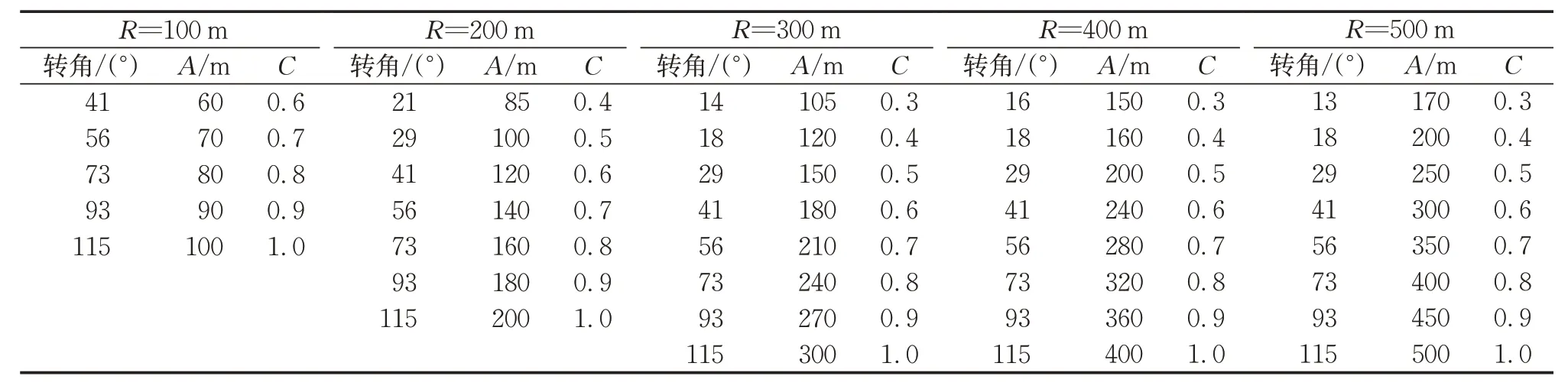
表2 回旋线参数设计值Tab.2 Design value of spiral parameters

1.4 受试者及实验方法

共招募24 岁至45 岁受试者15 人，男女比例为2∶1，其中专职驾驶员5 人，均为男性。实验前先让驾驶员在其中一个场景中进行预实验以熟悉实验环境。正式实验时，让驾驶员从每个场景的起点桩号起步向终点行驶完成左转测试，然后再由终点返回完成右转测试，驾驶过程中要求驾驶员尽量保持在本车道行驶。

2 回旋线长度对弯道车速影响分析

车辆的运行速度协调性与道路事故率存在显著的相关性，本节中主要研究车速随回旋线长度的变化规律。

2.1 弯道车速变化类型及分布规律

为了研究弯道的运行速度协调性，首先应准确把握路段车速变化模式，进而可以更加准确地计算速度协调性指标。根据仿真实验收集的数据，观察车辆在各个弯道上速度依桩号变化的规律，最终得到以下6种典型的车速变化模式（见图2）：

（1）下降型。车辆进入弯道前，驾驶员松开加速踏板或踩刹车将车速降低，进入弯道后车速持续下降，弯道全程既不踩刹车也不踩油门，速度变化率较低，多见于入弯车速不太高的驾驶员。

（2）V 型。车辆的实际减速点位于直缓点（ZH）前，运行车速先减小后增大，速度变化点往往位于圆曲线段。加速过程中的加速度绝对值往往高于减速过程。

（3）U型。驾驶员在第一回旋线段踩刹车减速，将车速维持在一个较低的水平进入圆曲线段，出弯时才进行加速操作。相比下降型和V 型，U 型在回旋线路段内的车速差和速度梯度均很大。此类型多见于入弯速度高，技术熟练的驾驶员。

（4）上升型。车辆在弯道内持续加速，此类型多见于入弯速度很低的情况。

（5）匀速型。车辆在弯道内速度变化平稳，与直线行驶相类似，波动范围在10 km·h-1以内。此类型多见于半径较大的曲线段。

（6）波动型。驾驶员在减速过程中不踩刹车，加速过程中加速度较小，加、减速的时间较长，区间内车速差较大，加速过程的加速度绝对值高于减速过程。该类型常见于回旋线及圆曲线长度较长的弯道。

图2 中，HY 是第一回旋线和圆曲线的切点，即缓圆点。YH 是圆曲线与第二回旋线的切点，即圆缓点。

以上6种车速变化模式虽然在不同半径和回旋线长度组合情况下都可能发生，但是发生频率受到上述2 种因素影响，呈现明显的规律性，如图3所示。

图3a 表明，半径100 m 弯道的速度曲线主要为下降型、V型和U型。当回旋线较短时，下降型所占的比例最大。随着回旋线长度的增加，下降型的比例逐渐减小，而V 型的比例逐渐增加。U 型占比随变量C变化不明显。

图3b表明，当回旋线长度较短时，半径200 m弯道的速度曲线主要为下降型、V 型和匀速型。随着回旋线长度的增加，下降型和匀速型的比例在逐渐减小，而V 型的比例呈先增大后减小的趋势。当C大于0.7时，波动型的比例急速上升。

图3c～e 则说明，在半径300 m、400 m 和500 m的弯道上，回旋线长度较短时，速度曲线的主要类型为V型、匀速型、下降型和少量的上升型。当回旋线长度增加时，匀速型、下降型和上升型的比例逐渐下降，V型的比例先增大后减小，当C大于0.4时，波动型的比例急剧上升。

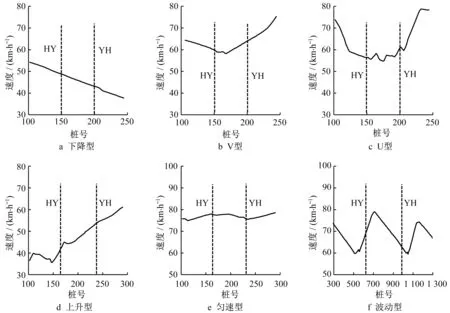
图2 弯道车速变化类型Fig.2 Types of speed changes in curves

综合图3 的结果还可以看出，不同类型速度曲线之间存在演化关系。随着回旋线增长和弯道转角增大，匀速型和下降型先向V型转化，当回旋线继续增长时，V 型再逐渐向波动型转化，因此图3b～e 中V 型的比例会呈现先增大后减小的趋势。匀速型、下降型、V 型和波动型的共同特点是驾驶员在减速过程中减速度变化平稳，可以认为前3 种类型的曲线均为波动型曲线在长度较短的弯道上的特例。

2.2 弯道速度协调性分析

《公路项目安全性评价规范》给出的二、三级公路弯道特征点速度计算方法并未考虑回旋线长度的影响［14］，因此针对半径相同、回旋线长度不同的弯道，只要入弯的初始速度相同，路段车速差|Δv|的结果也相同。第2.1 节的结果显示，半径和回旋线长度都显著影响速度变化模式，因此若按规范提供的方法进行计算，可能会高估路段的运行车速一致性。本节中旨在研究运行速度协调性指标随回旋线长度的变化规律。

中方：文化和旅游部、全国红色旅游工作协调小组成员单位、山东省文化和旅游厅、有关省（区、市）旅游主管部门；18个红色旅游重点城市代表；全国红色旅游经典景区代表；省内17个地市旅游委(局)代表；全国重点旅行社代表；红色旅游专家；中央、省、市新闻媒体记者；临沂市有关领导，旅游企业代表等。

路段的85%分位车速差|Δv85|和速度梯度|IΔv|是评价路段运行速度协调性的常用指标，计算式如下所示：

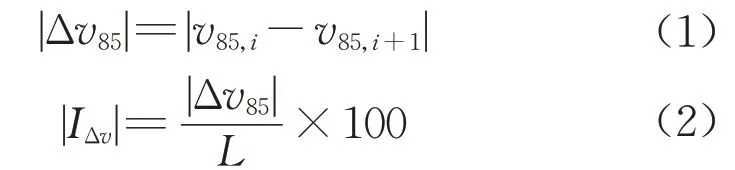
式中：v85，i为路段起点的85%分位运行车速，i=1，2，3，…；v85，i+1为路段终点的85%分位运行车速；L为起点到终点的长度。计算前需要先对路段进行划分，《公路项目安全性评价规范》规定二、三级公路平曲线路段的划分方法（下文简称为曲线特征点法）为：从曲中点（QZ）将曲线分成2段，分别计算直缓点（ZH）、曲中点（QZ）和缓直点（HZ）的运行车速，进而得到|Δv85|和|IΔv|。由第2.1节的结果可知，很多情况下车辆的实际减速点位于直缓点前方；另外，不同长度弯道的运行速度变化模式是不同的，当曲线较长时，速度曲线整体向波动型演化，而车速仅会在路段的某一局部有较大的增减。因此，如果采用曲线特征点法可能捕捉不到上述特征。定义一种新的计算方法（下文简称局部单调变速区间法）：从曲中点将路段一分为二，以直缓点前的实际变速点为计算起始点，截取一次单调车速变化中速度差最大的区间（见图4），用区间的最大、最小速度计算车速差|Δv|，并结合2个速度点之间的距离计算|IΔv|。

将上述2种方法计算的|Δv|和|IΔv|作为因变量进行85%分位线性回归，自变量选取回旋线参数A、曲线半径R及转向D。因A与R存在交互效应，将2个变量合并为C=A/R。其中，D为二分变量，左转弯时取0，右转弯时取1。回归结果如表3所示。

8个模型的综合系数F检验p值均小于0.01，说明模型整体有统计学意义。D与|Δv|、|IΔv|的相关性均不显著，故予以剔除。

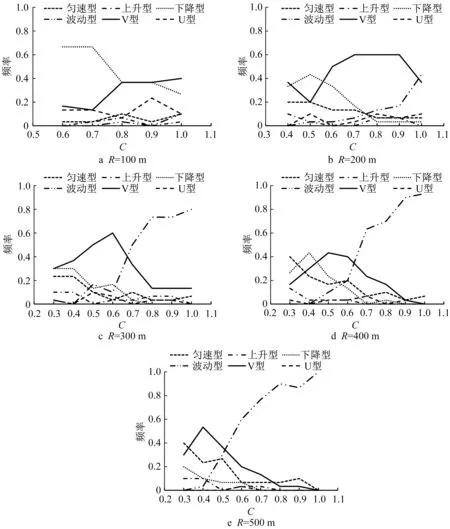
图3 各型速度曲线在不同弯道上的出现频率Fig.3 Frequency of each type of speed curve on different curves

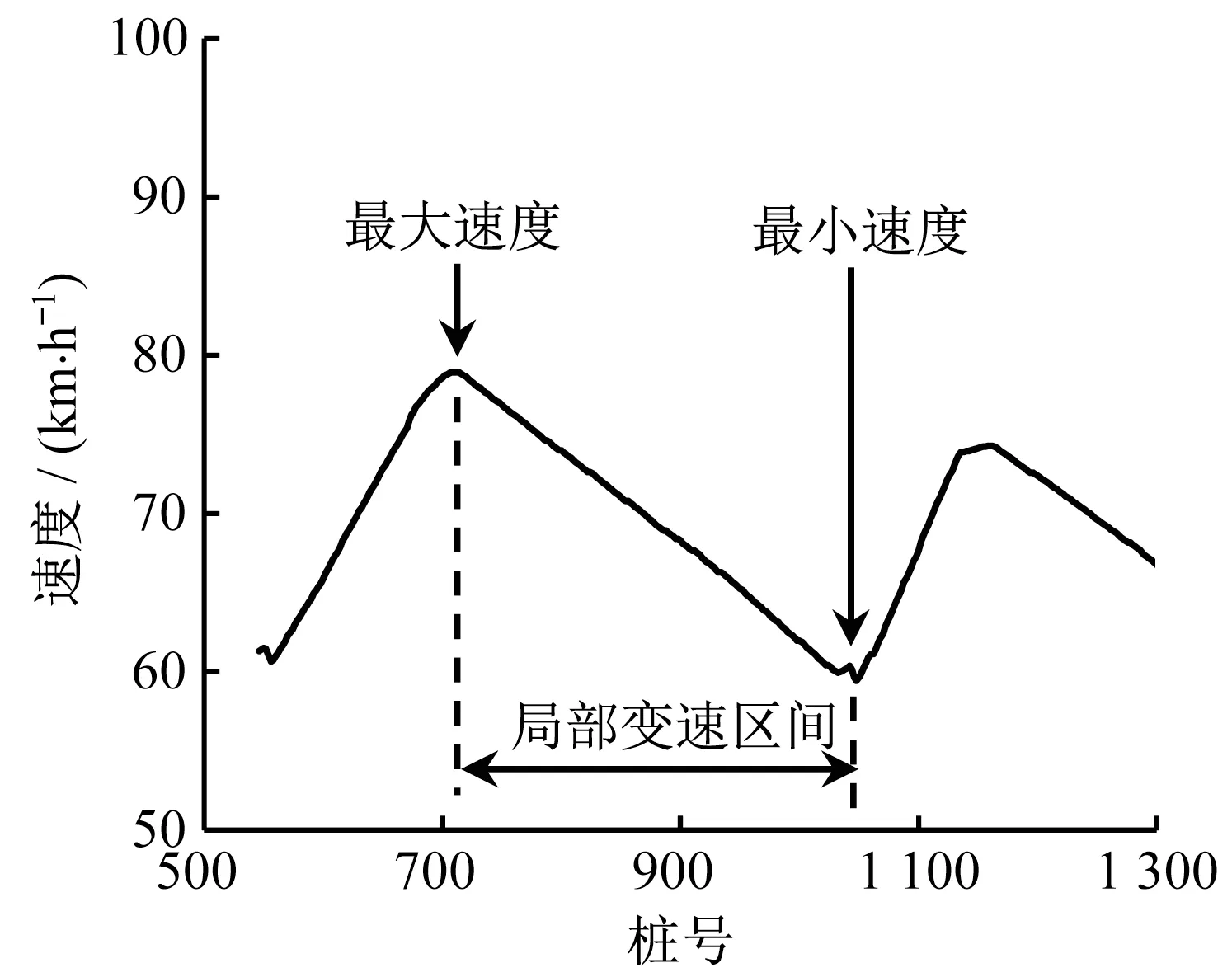
图4 局部单调变速区间Fig.4 Local monotone interval of speed-change

针对路段车速差|Δv|，在85%分位水平上，2 种方法计算得到的变量C的系数差异明显。ZH至QZ路段，C的系数分别为14.037和23.293，表明R一定时，A每增长0.1R倍，起终点速度差就会上升约1.40 km·h-1，而最大最小速度差则会上升2.33 km·h-1；在QZ 至HZ 路段，C的系数分别为12.509 和21.039。这说明，A每增长0.1R倍，起终点速度差就会上升约1.25 km·h-1，而最大最小速度差会上升约2.10 km·h-1。

针对路段车速梯度|IΔv|，在85%分位水平上，ZH至QZ路段2种方法求得的C的系数分别为-3.469和-2.096，但局部单调变速区间法C的系数不显著（p=0.357＞0.005），说明最大最小速度点间的速度梯度与回旋线长度不显著相关。曲线特征点法的回归结果表明在R一定时，A每增长0.1R倍，路段起终点间的速度梯度就会下降约0.35 km·（m·h）-1。在QZ 至HZ 路段，变量C的系数分别为-7.345 和-7.429，说明A每增长0.1R倍，路段起终点间的速度梯度会下降约0.73 km·（m·h）-1，最大最小速度点间的速度梯度下降约0.74 km·（m·h）-1，两者差异不明显。

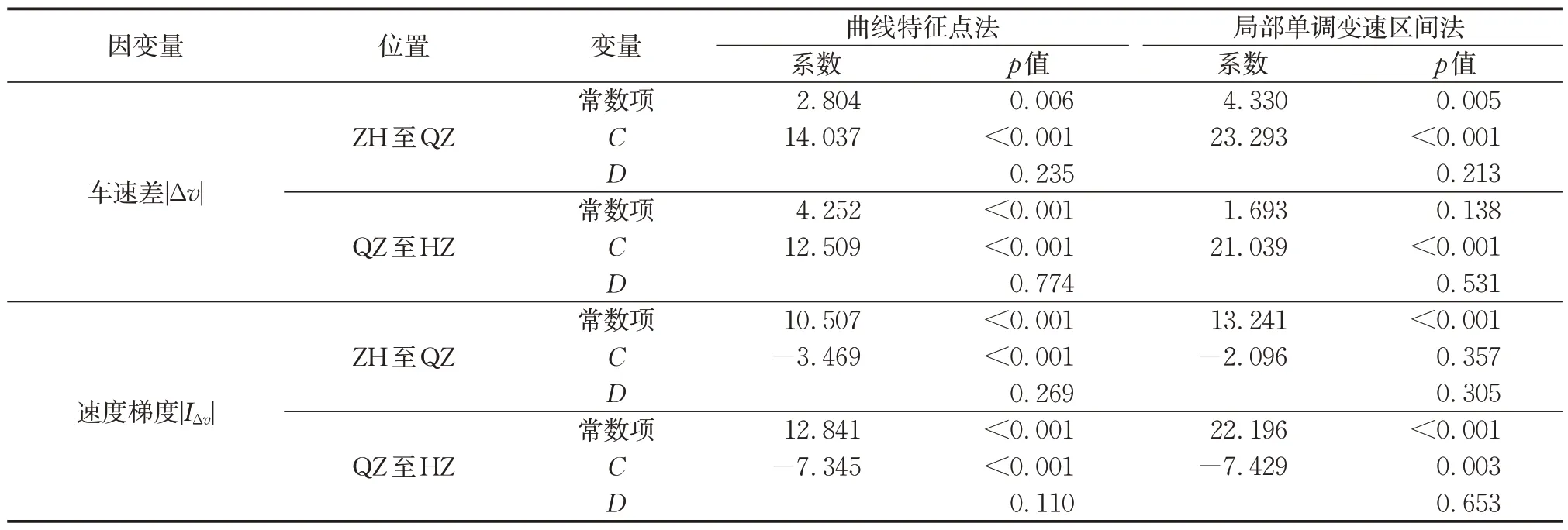
表3 85%分位回归结果Tab.3 Results of 85%quantile regression

3 回旋线路段行驶轨迹分析

车辆轨迹的稳定性是影响行车安全的另一个重要因素，本节中主要从轨迹波动特征和局部曲率2个方面进行分析。

3.1 轨迹的波动特征

针对车辆轨迹的波动特征，主要研究波动的幅度和频率，具体方法为：以1 m 为步长，将每个桩号对应的侧向偏移x与桩号进行匹配以构造空间信号序列x，然后将信号变换到空间频域进行分析。因车辆在各个桩号上的侧向偏移是一个随机变量，因此x是功率信号，对该序列的频域分析主要依据其功率谱密度函数。车辆在弯道行驶时侧向位置的期望因驾驶员而异，并不一定和车道中心线重合，这个期望值构成了空间序列的直流分量，但不包含车辆轨迹波动的信息。在变换到频域之前要先对序列进行去均值化处理，将其转换为期望为零的信号，如下所示：

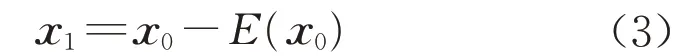
式中：x1为去均值化后的侧向偏移空间序列；x0为原始序列；E(x0)为原始序列的期望。根据Wiener-Khinchin 定理，信号的功率谱密度函数是其自相关函数的傅里叶变换，如下所示：

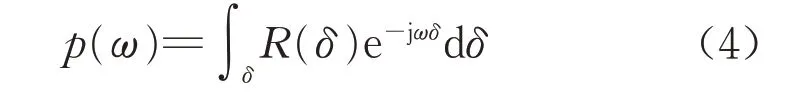
式中：p(ω)为信号的功率谱密度函数；ω为信号的空间频率；R(δ)为信号的自相关函数；δ为空间延迟距离。图5 为某样本的侧向偏移功率谱密度函数曲线。横坐标为空间频率，即单位长度上车辆侧向偏移的波动频率。

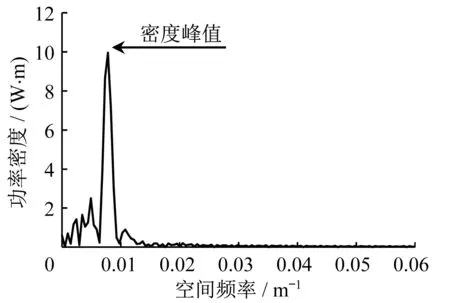
图5 功率谱密度函数曲线Fig.5 Power spectral density function curve

对功率谱密度函数在空间频率上积分即可得到信号的平均功率W，W表征了信号的平均振幅，表示车辆轨迹相对于平衡位置波动的侧向偏移的平均水平。功率密度的计算式如下所示：

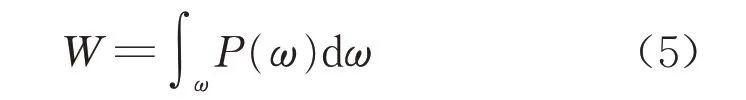
式中：W为信号的平均功率。功率谱密度函数最大峰值对应的空间频率反映了较大幅度的偏移值在单位长度行程上出现的次数（见图5），代表轨迹的整体波动频率。计算所有车辆在各弯道上轨迹的侧偏平均功率W及最大峰值频率2 个指标，其均值随C的变化趋势如图6和图7所示。

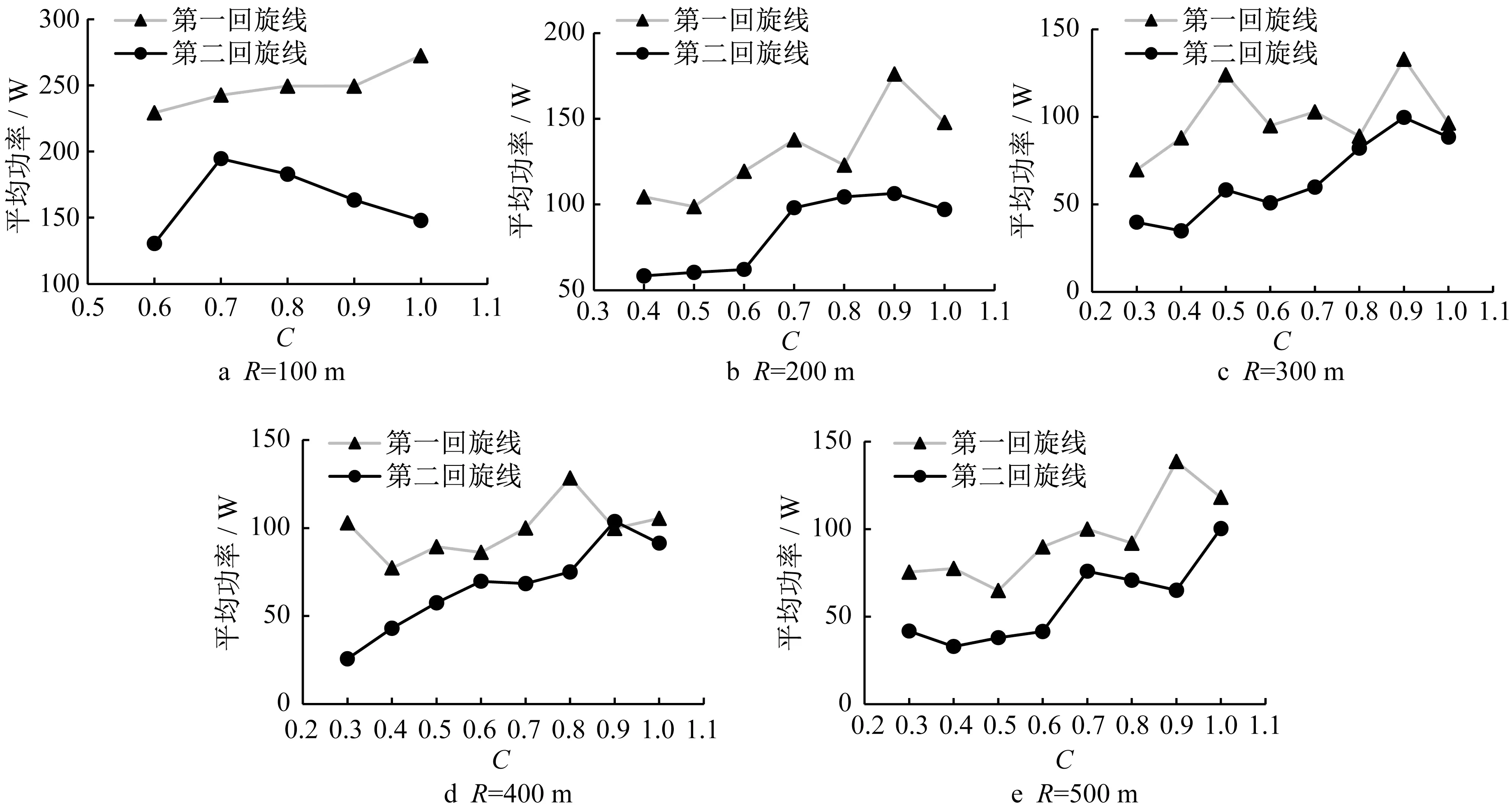
图6 回旋线路段侧偏信号平均功率Fig.6 Average power of lateral offset on spiral transitions

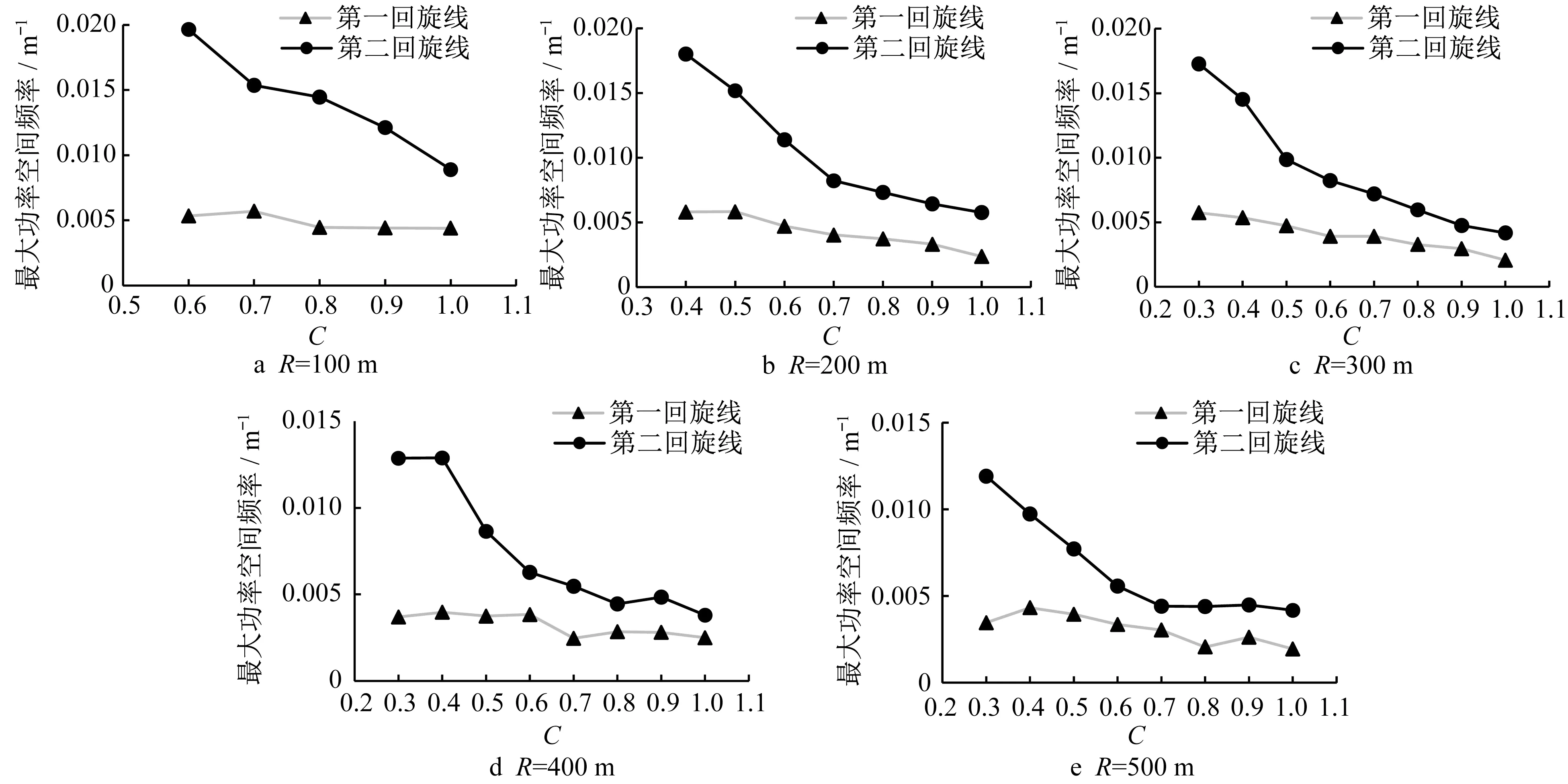
图7 回旋线路段侧偏信号功率密度峰值频率Fig.7 Peak frequency of power density of lateral offset on spiral transitions

图6 结果表明，半径100 m 的曲线组，随着回旋线长度的增加，车辆入弯时的平均偏移量呈上升趋势，而出弯时平均偏移量则先增大后减小。半径200 m的曲线组，车辆入弯和出弯时的平均偏移量均呈波动上升趋势，当C大于0.6时上升速度加快，但总体偏移水平较100 m 半径组低。半径大于等于300 m的3个曲线组，车辆入弯和出弯的平均偏移也均呈波动上升趋势，在C大于0.4时上升速度增加。3 个曲线组的总体偏移水平较200 m 半径组低，但3个组之间无明显差异。相同几何条件下，出弯时的平均偏移水平均小于入弯。

图7 结果表明，车辆大幅度偏移出现的次数会随着回旋线长度的增加而下降。这说明，回旋线越长、曲率变化越平缓，车辆轨迹的波动频率越低。对比第一回旋线和第二回旋线的结果可知：当回旋线较短时，车辆出弯时的轨迹波动频率比入弯时高得多，随着回旋线长度的增加，虽然2条线有逐渐接近的趋势，但是整体还是出弯时的波动频率高一些。结合图6 的结果，说明出弯时驾驶员对车辆轨迹的修正次数较多，这也是其平均偏移水平较入弯时低的原因。

综上所述，回旋线长度显著影响车辆轨迹的波动幅度和频率。总体上看，回旋线长度增加，车辆轨迹的平均波动幅度也会随之增加，但波动频率则会随之下降。

3.2 轨迹的局部曲率

弯道行驶中车辆的侧向偏移是在某一平衡位置附近波动的，所以车辆轨迹的曲率会大于路线的实际曲率，从而产生一个附加的侧向加速度。当这个侧向加速度与转向加速度同向时，对车辆的侧向稳定性有一定的负面影响，尤其是在道路湿滑侧向摩阻下降的时候会增加车辆侧滑的风险。为了研究车辆轨迹的局部曲率的变化规律，以车道轴线为y坐标，与y正交的方向为x坐标，垂直路面的方向为z坐标，建立三维坐标系。规定垂直路面向上的方向为z轴的正方向。采用三点法计算侧偏空间序列的局部曲率，如图8所示。

图8 三点法求解局部曲率Fig.8 Three-point method for local curvature

M、N、O是轨迹上的3个连续点，从M点至O点的方向为前进方向。a是M点到N点的向量，b是M点到O点的向量，则弧MO的曲率半径

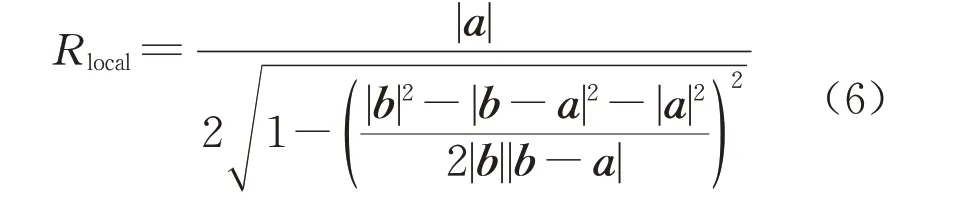
曲率的方向由a和b的外积的方向决定。当车辆左转、a×b与z轴正方向相同时，Rlocal的符号为正；对于车辆右转，a×b与z轴正方向相反时Rlocal的符号为正。将各个车辆在各回旋线上的同向最大局部曲率均值绘制成折线图，如图9所示。

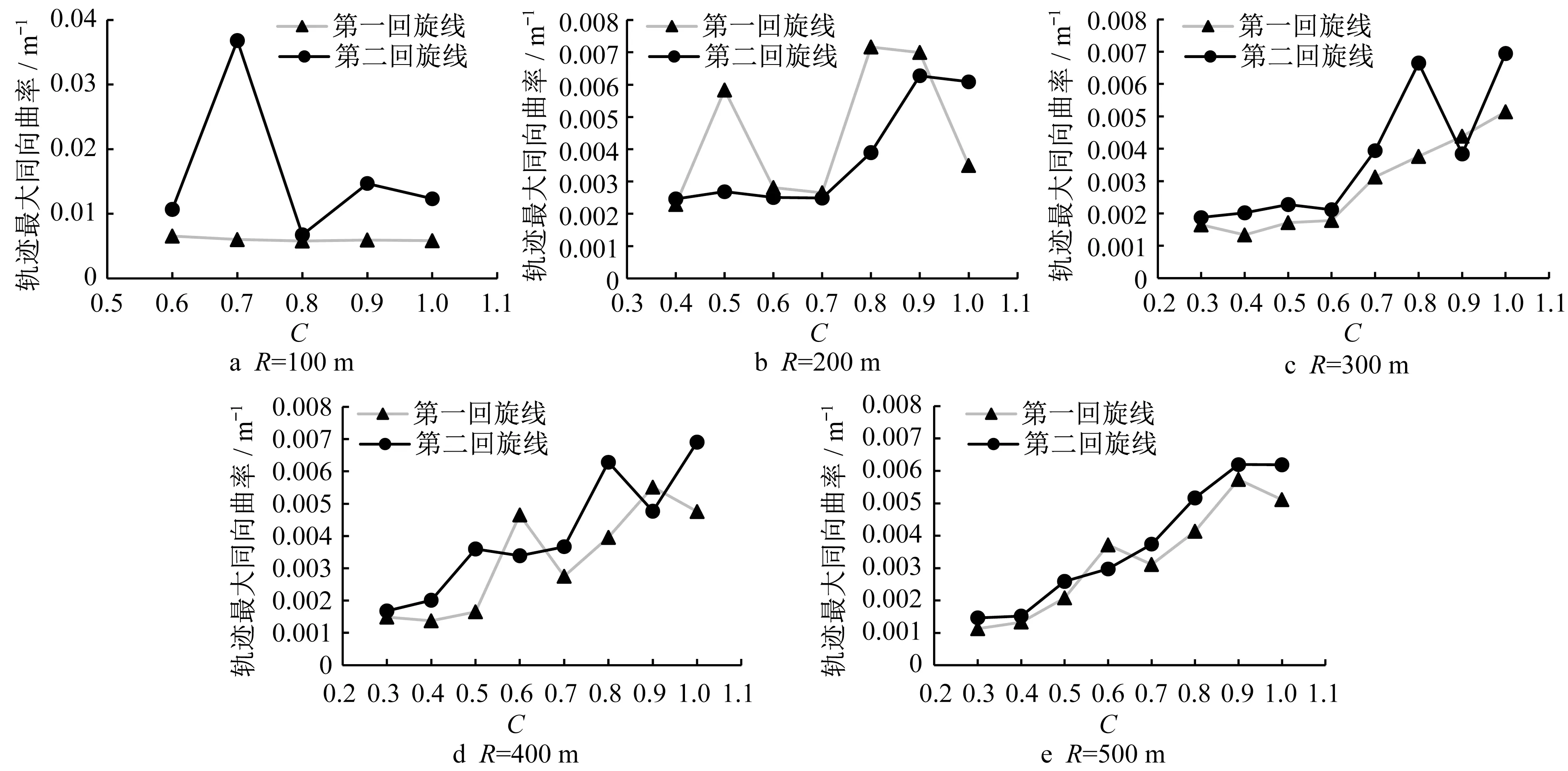
图9 回旋线路段轨迹最大同向局部曲率Fig.9 Maximum local curvature in the same direction of horizontal curve on spiral transitions

图9 结果表明，半径100 m 的曲线组，随着回旋线长度增加，入弯时的最大同向曲率变化较稳定，并且呈缓慢下降的趋势。出弯时的最大同向曲率变化趋势有明显的波动性，呈左边高右边低的形态。半径200 m 的曲线组，入弯时的最大同向曲率变化趋势呈两头高中间低的形态，出弯过程中当C小于等于0.7时同向曲率变化不大，当C大于0.7时则急剧增加。半径大于300 m的3个曲线组，出弯和入弯时的同向最大曲率总体随C值的增加而增加。

4 结论

（1）车辆在弯道行驶时速度的变化模式主要有以下6种类型：下降型、V型、U型、上升型、匀速型和波动型。各种类型所占的比例随回旋线长度的增加而变化，并且存在相互演化关系。当回旋线长度较短时，车速的变化模式以下降型、匀速型和V 型为主，伴有少量的U 型和上升型。当回旋线长度增加时，下降型和匀速型先向V型转化，若回旋线长度继续增加，则V型会逐渐演化为波动型。

（2）半径相同时，回旋线长度增加会增大路段出入口车速差和最大最小车速差，后者增长的幅度高于前者，而速度梯度随着回旋线增长而下降。

（3）半径相同时，回旋线长度增加导致车辆轨迹的波动幅度增大，但会使波动的频率降低。

（4）半径为100 m时，回旋线太短使轨迹的局部曲率增大，半径为200 m时，回旋线太短或太长均会造成轨迹局部曲率升高，而半径为300 m 及以上的弯道，回旋线越短，轨迹的局部曲率越低。

（5）不同半径的曲线对回旋线的长度需求是不同的。综合车速、轨迹特征的分析结果可知：半径为100 m 时，C宜取0.8～1.0；半径为200 m 时，C宜取0.6～0.7；半径大于等于300 m时，C以小于等于0.6为宜。

该结论适用于双车道公路半径为100～500 m、视距良好的平曲线路段。下一步研究将考虑增加纵坡和竖曲线的影响。

作者贡献声明:

袁 方：实验场景的设计、建模和数据采集，数据分析、建模及论文撰写。

杨 轸：数据分析，论文修改与定稿。