共轭梯度法在弹塑性模型数值实现中的应用

代 宁，耿大将，郭培军，周顺华，狄宏规

（1.同济大学道路与交通工程教育部重点实验室，上海 201804；2.同济大学上海市轨道交通结构耐久与系统安全重点实验室，上海 201804；3.新城控股集团股份有限公司上海第二分公司，上海 201800；4.麦克马斯特大学土木工程系，汉密尔顿L8S4L7）

弹塑性本构模型的数值算法主要包括显式算法与隐式算法两大类。通常，显式算法［1-3］计算精度较低，实际应用少，而隐式算法计算精度较高，能实现自校正，不会发生误差传递，实际应用普遍。隐式算法一般采用弹性预测-塑性修正算法，在塑性修正步一般会用牛顿-最近点投影法（Newton-CPPM）求解回退映射非线性方程组，而Newton-CPPM 需确保Jacobian 矩阵是可逆矩阵，否则无法进行求解。同时，Newton-CPPM 是一种局部收敛性算法，迭代初值选取的合理性直接影响算法收敛性。因此，Jacobian 矩阵奇异与Jacobian 矩阵不收敛是用传统隐式算法进行高度非线性弹塑性本构模型数值实现所遇到的主要问题。

针对该问题，国内外学者开展了许多研究并取得了一定进展。通常，在采用具有局部收敛性的Newton-CPPM 时，只要所选取的初值十分接近真实解，该算法最后总可以收敛到问题的真解。因此，为改进算法的迭代初值，Bicanic 等［4］和Stupkiewicz等［5］采用辅助投影面法初步解决了迭代初值的合理选取问题。然而，针对如何有效地建立辅助投影面这个问题，其并未做出很好的解答。Valentini等［6］、Jia［7］、Majid 等［8］、Penasa 等［9］、Wang 等［10］、Lee等［11］采用多步法，即先将一个增量步分为多个增量步，再对方程进行求解，最终实现了迭代初值的改进。然而，该方法显然会大幅增加计算量，从而降低计算效率。Hernandez 等［12］采用显式方法实现了对部分状态变量迭代初值的改进，然而该方法仍未解决对于改进哪些状态变量的迭代初值就可以有效改进算法收敛性的问题。因此，为改善收敛性，耿大将等［13］引入同伦算法以改善收敛性并避免Jacobian 矩阵奇异。为了避免Jacobian 矩阵求解时巨大的计算量，Homel等［14-15］和Sharifian等［16］采用分阶段迭代算法来求解高度非线性回退映射方程组，首先求得一致性参数，再将一致性参数视为已知量，最终求解其余状态变量。值得注意的是，单独应用分阶段迭代算法求解方程组仍存在结果不收敛问题，对于高度非线性的本构模型，不收敛问题更加显著。此外，在求解非线性回退映射方程组方面，Bilotta 等［17］、Placidi［18］、Armoro［19］也做了大量工作，主要采用优化方法或搜索技术，而这类方法的计算特点是计算过程复杂、计算量较大，故该方法在弹塑性本构模型数值实现中的应用十分有限。

尝试用共轭梯度法［20-22］对传统隐式算法进行改进，以避免在高度非线性弹塑性本构模型的隐式算法实现中出现Jacobian矩阵奇异和不收敛问题。

1 传统隐式算法

弹塑性本构模型的数值实现主要包括状态变量的更新与一致切线刚度的计算两部分内容。

1.1 状态变量的更新

在隐式算法对弹塑性本构模型进行状态变量更新的过程中，第（n+1）个增量步所对应的基本方程如下所示：

式中：σ和Δε分别为应力和应变增量；C为弹性刚度；Δλ为一致性参数；r为塑性流动方向；ξ和分别为硬化内变量和相应的硬化方向；φ为屈服函数。以应力σ为自变量，对塑性势函数求偏导即可得出塑性流动方向r。硬化内变量可以有多个，具体数量取决于具体的本构模型。

状态变量更新的过程实际上就是在满足Δλ≥0的前提下对以σn+1、ξn+1和Δλ为自变量的回退映射非线性方程组式（1）进行求解的过程。目前，多采用弹性预测-塑性修正算法进行求解，求解过程主要包括以下三个步骤。

（1）弹性预测。

带下标tr 的量表示的是经弹性预测后得出的状态变量。

（2）塑性检验。如果φtr，n+1≤0，这说明材料处于弹性状态，否则应该进行塑性修正。

（3）塑性修正。一般采用Newton-CPPM 求解以σn+1、ξn+1和Δλ为未知量的非线性方程组式（1），迭代初值一般取为弹性预测后所得状态变量的值，如下所示：

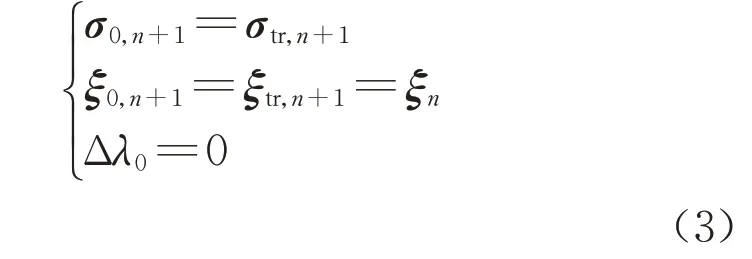
在率无关弹塑性力学框架内建立或改造本构模型主要可以通过以下两种途径实现：提高弹性关系、屈服函数、塑性势函数或硬化规则的复杂程度，适当增加内变量。如对于结构性软土的弹塑性本构模型，为反映土体结构性的影响，祝恩阳等［23］、Suebsuk等［24］和Dafalias 等［25-26］均在经典修正剑桥模型［27］（MCC）的基础上进行了改进。

无论采用哪种改进模式均会导致回退映射方程组式（1）非线性程度的提高。式（1）的第一式中包含弹性刚度Cn+1和塑性流动方向rn+1，当弹性刚度Cn+1的表达式中包含应力σn+1时，显然第一式的非线性程度会提高；当塑性势函数的复杂程度提高或内变量增加时，相应的塑性流动方向rn+1的复杂程度也会提高，所含内变量的数量也会增加，同样会导致第一式非线性程度的提高。第二式主要反映的是硬化规则的影响，包含硬化方向，当硬化规则的复杂程度提高后，显然第二式的非线性程度会提高，当内变量的数目增加时，第二式中所含等式的数量会做相应的增加，显然也会造成第二式非线性程度的提高。第三式主要体现的是屈服函数，屈服函数变复杂时，第三式的非线性程度显然会提高。

当要进行数值实现的弹塑性本构模型非线性程度较高时，相应的回退映射方程组式（1）的非线性程度也会较高。对于高度非线性的弹塑性本构模型，采用隐式的弹性预测-塑性修正算法进行状态变量更新容易出现Jacobian 矩阵奇异和不收敛问题。这是因为弹性预测-塑性修正算法主要是基于Newton-CPPM，而Newton-CPPM 是一种局部收敛方法，只有当初值接近于问题的真解时收敛性才较好，同时Newton-CPPM 必须保证Jacobian 矩阵是可逆的。对于高度非线性的回退映射方程组式（1），这两点都很难保证。结合方程组式（1）的构成和Newton-CPPM的特点可以看出，可能导致Jacobian矩阵奇异或不收敛的原因有以下几个方面：

（1）弹性预测点离真解较远。例如，对于同时可以考虑硬化和软化的模型，当真解在软化区，而根据弹性预测得出的迭代初值在硬化区，这种情况下可能导致Jacobian矩阵奇异或不收敛。

（2）组成回退映射方程组式（1）的方程数量级相差较大。例如，考虑软土结构性的Saniclay 模型［26］，包含表示旋转硬化的内变量，数量级为10-1左右，包含表示结构性的内变量，数量级为100～101，包含表示各向同性硬化的内变量，数量级可以达到102以上，将数量级相差较大的方程组成方程组然后求解，可能导致Jacobian矩阵奇异或不收敛。

（3）弹性刚度较为复杂。例如，修正剑桥模型的弹性刚度依赖于静水压力，属于压力依赖型模型，可能导致不收敛。

（4）硬化规则较为复杂导致局部迭代过程中硬化内变量的改变过大。例如，修正剑桥模型中代表屈服面大小的硬化内变量在迭代过程中可能由正值转化为负值，导致不收敛。

（5）应力空间中，屈服面或塑性势面的曲率较大或存在尖角。例如，考虑软土结构性的Saniclay模型的屈服面和塑性势面曲率比较大，Mohr-Coulomb模型的屈服面存在尖角，可能导致Jacobian 矩阵奇异或不收敛。

1.2 一致切线刚度的计算

当状态变量在弹性或弹塑性状态时，相应的一致切线刚度D显然是不同的。

（1）弹性状态时，对于σn+1和εn+1，两者均满足方程σn+1-σn-Cn+1∶Δεn+1=0，将σn+1和Δεn+1同时视为变量，对该式微分，即可确定一致切线刚度。

（2）弹塑性状态时，σn+1和εn+1满足回退映射方程组式（1），将σn+1、ξn+1、Δλ、Δεn+1视作变量，对该方程组微分，得到微分方程组，然后消去dξn+1与dΔλ即可得到dσn+1和dΔεn+1间的关系，从而确定一致切线刚度。

2 改进隐式算法

弹塑性本构模型数值实现的关键在于状态变量的更新，而状态变量的更新关键在于塑性修正步。传统的隐式算法在塑性修正步中需要采用Newton-CPPM 求解回退映射非线性方程组，但不能保证迭代初值位于收敛域内，更不能保证Jacobian 矩阵可逆，对于高度非线性的弹塑性本构模型更是如此。

为了避免由于组成回退映射方程组的方程数量级相差较大而造成迭代过程的不收敛，将式（1）修正为

式中：ρξ和ρφ表示权重系数。当迭代初值取为弹性预测结果时，权重系数的取值要能保证组成方程组（4）的各个方程对应的残差位于同一数量级。显然，方程组（1）和（4）的解是完全相同的。

即便对高度非线性的方程组式（1）做如式（4）所示的修正，仍无法完全避免迭代求解过程的不收敛（这是由Newton-CPPM 的局部收敛性所决定的），更无法避免Jacobian 矩阵奇异问题。为此，将方程组式（4）简记为

式中：x=(σn+1，ξn+1，Δλ)T。在解存在且唯一的情况下，方程组式（5）的解等价于如下最小化问题的解：

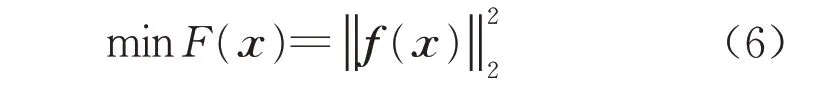
共轭梯度法对应的迭代公式为

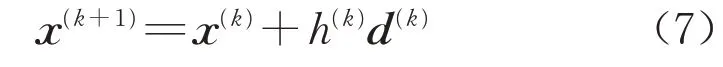
上标（k+1）和k分别表示第（k+1）次和第k次迭代。步长h(k)由下式得出：

搜索方向d(k)由下式得出：

式中：∇F为函数F(x)的梯度；βk-1为计算因子；gk为函数F(x)在x=x(k)处的梯度。

采用改进隐式算法求解回退映射方程组式（1）的过程如图1 所示。求解过程中，首先考虑数量级问题，将方程组式（1）修正为式（4），然后将弹性预测结果作为塑性修正步的迭代初值，用Newton-CPPM 求解方程组式（4），求解过程中出现Jacobian矩阵奇异或不收敛问题时，用共轭梯度法求解方程组式（4）对应的最小化问题式（6），将求得结果作为改进后的迭代初值，再次采用Newton-CPPM 求解方程组式（4）。由于共轭梯度法是大范围收敛算法，因此可以有效避免Newton-CPPM所存在的不收敛问题。从共轭梯度法的求解过程可以看出，整个过程不需要进行矩阵求逆运算，因此也不会存在Jacobian矩阵奇异问题。综上，改进隐式算法可以同时解决不收敛或Jacobian矩阵奇异问题。

3 隐式算法比较

理论上，改进隐式算法可以同时解决传统隐式算法在高度非线性弹塑性本构模型数值实现中所存在的不收敛和Jacobian 矩阵奇异问题，但实际效果如何还有待检验。考虑软土结构性的Saniclay 模型具有较高的非线性，属于压力依赖性模型，该模型的塑性势面和屈服面的曲率较大，含有多达五个的硬化内变量，而且硬化内变量的数量级相差较大，硬化规则的非线性程度较高，该模型也可以同时考虑硬化和软化效应。因此，以该模型为例对传统隐式算法和改进隐式算法进行计算精度、收敛性和计算效率的对比。

图1 改进隐式算法Fig.1 Improved implicit algorithm

对比分析建立在单元体分析基础上，计算中所采用的初始应力状态和加载应变路径分别如表1和表2 所示。表2 中，εa和εr分别表示轴向应变和径向应变。计算中建立单个三维八节点实体单元，本构模型参数取值参考文献［13，26］。

如表3和表4所示，每种初始应力状态对应的每种变应变路径均采用两种算法进行数值计算，并且每种算法均考虑了10-1、10-2、10-3和10-4等四种增量步长In。表3、4 中，×表示结果不收敛，√表示结果收敛。对每种情况下的收敛性Cov、计算时间t、广义剪应力q的终值qt进行统计对比。qt-εq曲线如图2～5 所示。图2～5 中，表示广义剪应变，其中J2ε表示偏应变张量第二分量。

表1 初始应力状态Tab.1 Initial stress state

通过对应力-应变曲线的对比发现，对于特定的初始应力状态、特定的应变路径和特定的步长，在收敛情况下，传统隐式算法（K0）和改进隐式算法（K1）总能得到近乎完全相同的结果，如图2～5 所示。这是因为在初始应力状态、应变路径及步长相同的情况下，两种算法所对应的基本方程都是式（1），在该方程的解存在且唯一的情况下，精度控制相同时，不论采用哪种算法，计算结果理应一致。

表2 应变路径Tab.2 Strain path

表3 初始应力状态K0计算结果对比Tab.3 Comparison of calculation results under initial stress state K0

表4 初始应力状态K1计算结果对比Tab.4 Comparison of calculation results under initial stress state K1

对传统隐式算法，当采用平面应变加载模式时，即使增量步减小到10-4时，仍然不收敛；当采用不排水加载模式时，增量步减小至10-4时，才会达到收敛。这说明，对于高度非线性弹塑性本构模型，传统隐式算法对步长有很强的依赖性且收敛性很差。图6 为初始应力状态K0 和平面应变路径下增量步为10-2时某一增量步迭代误差Δ随迭代次数n的变化。从图6 可以看出，改进隐式算法收敛性明显优于传统隐式算法。这是因为传统隐式算法在求解弹塑性本构模型中的高度非线性方程组时，对于局部收敛的Newton-CPPM，较大的增量步使弹性预测所得的迭代初值很难位于收敛域内，因此极易出现不收敛现象。

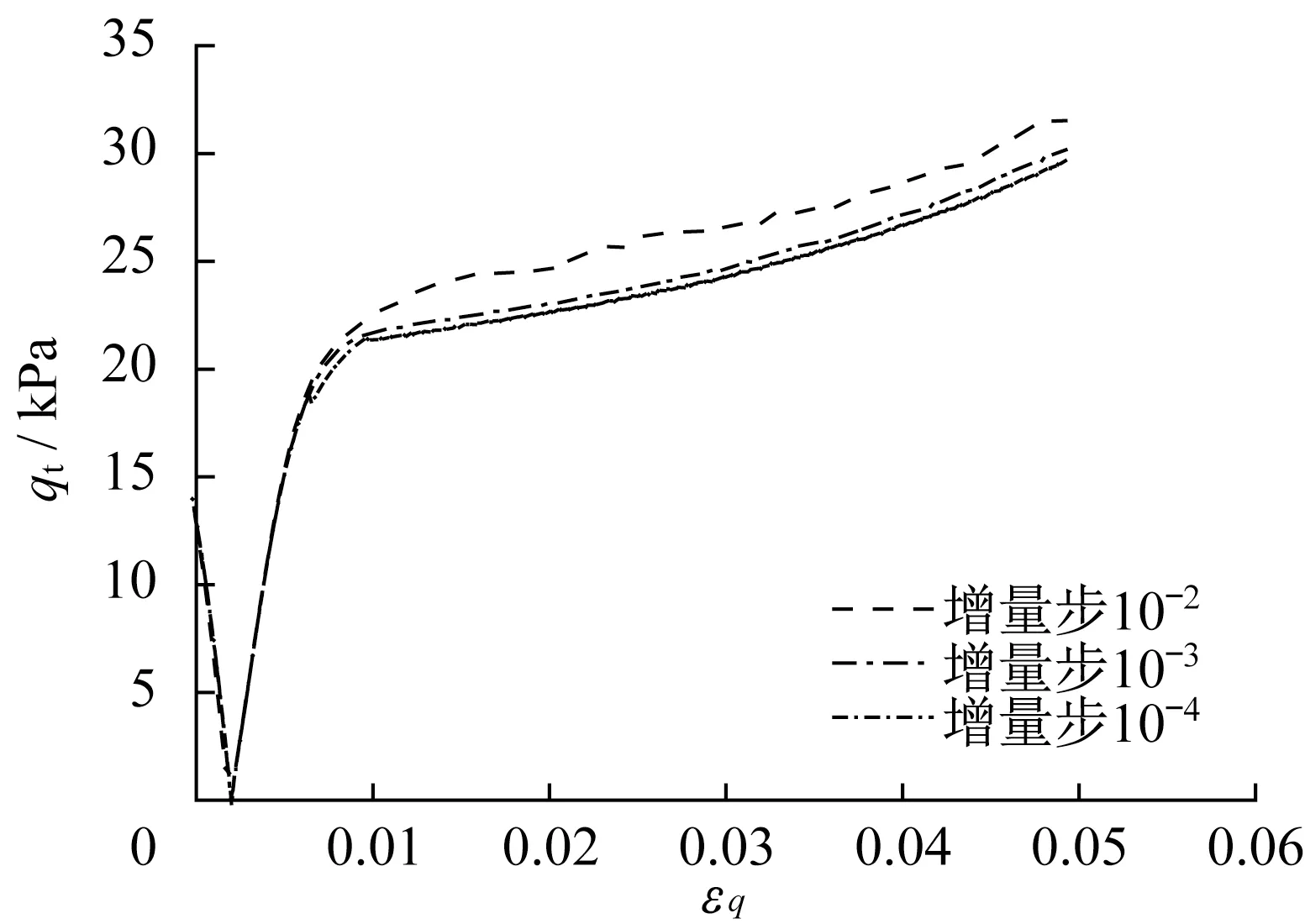
图2 初始应力状态K0下平面应变加载所得qt-εq曲线Fig.2 qt-εq curve under initial stress state K0 and plane strain loading

图3 初始应力状态K0下不排水加载所得qt-εq曲线Fig.3 qt-εq curve under initial stress state K0 and undrained loading

对于改进隐式算法，当采用平面应变加载模式时，增量步为10-2时即可收敛；当采用不排水加载模式时，增量步为10-1时即可收敛。显然，改进隐式算法基本不依赖于步长且收敛性好。原因在于，改进隐式算法中高度非线性方程组的求解问题转化为最小化问题，通过采用具有全局收敛性的共轭梯度法求解最小化问题，使得结果收敛性较好。

图4 初始应力状态K1下平面应变加载所得qt-εq曲线Fig.4 qt-εq curve under initial stress state K1 and plane strain loading

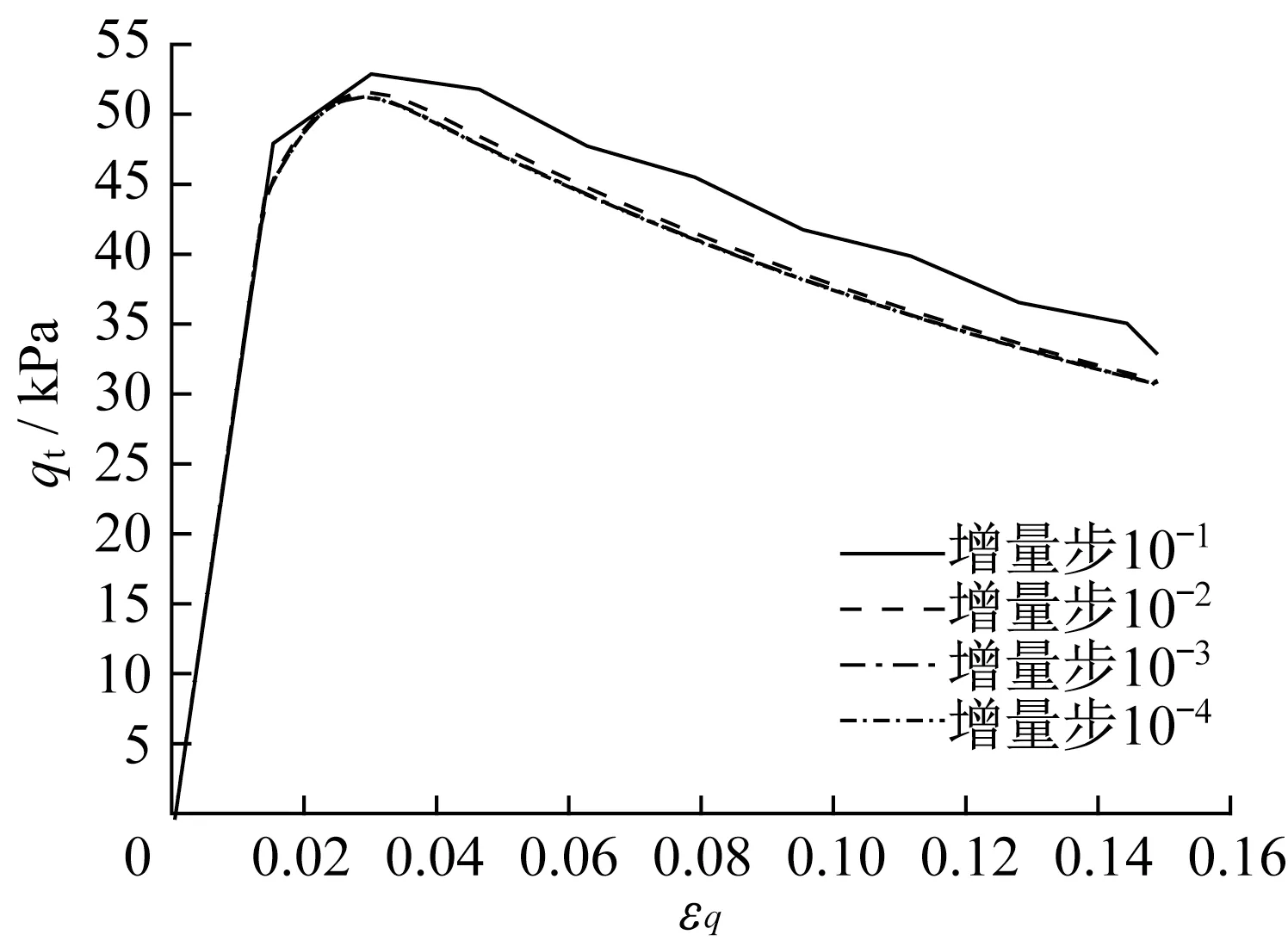
图5 初始应力状态K1下不排水加载所得qt-εq曲线Fig.5 qt-εq curve under initial stress state K1 and undrained loading

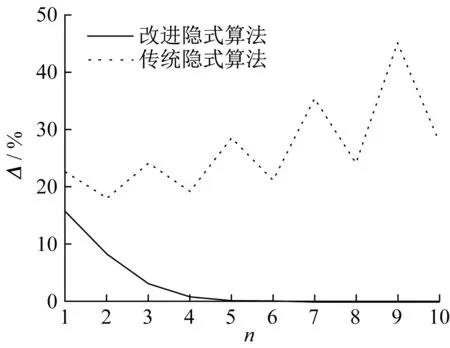
图6 两种算法收敛性对比Fig.6 Comparison of convergence between two algorithms

在同样的初始应力状态、加载路径及增量步长下，当两种算法均收敛时，如初始应力状态K0 不排水加载条件下，当增量步为10-4时，改进隐式算法采用传统的Newton-CPPM可以成功求解高度非线性方程组，而不需要采用共轭梯度法求解相应的最小化问题，此时改进隐式算法则退化为传统隐式算法，因此两种算法计算效率理应相同。为了节约计算时间，实际工程计算中常采用变步长方法，因此有必要对变步长情况下两种算法的计算效率进行比较。如初始应力状态K0不排水加载时，传统隐式算法在增量步为10-4时可以收敛，对应计算时间为310.70 s；改进隐式算法在增量步为10-1时可以收敛，对应计算时间为0.20 s。显然，整体上改进隐式算法比传统隐式算法计算效率要高得多。

综合以上分析，与传统隐式算法相比，改进隐式算法收敛性好，整体计算效率高，计算精度基本相同。显然，改进改进隐式算法能够很好地解决传统隐式算法所存在的Jacobian矩阵奇异和不收敛问题。

4 算例

基坑开挖是土木工程领域常见的工程行为，以如图7 所示的一小型无支护的基坑开挖为实例，基坑宽4.00 m，开挖深度4.00 m，考虑对称性建立一半模型进行计算。基坑土体分两层，上部硬层采用Mohr-Coulomb 模型，下部软土层采用考虑土体结构性的Saniclay模型，具体模型参数的取值如表5所示，表5中各模型参数的物理意义可参考文献［26］。计算过程主要包括两个分析步，第一步为地应力平衡，第二步进行基坑开挖及钢板桩施做，采用单元移除和激活功能实现开挖模拟和钢板桩施做。

图7 几何模型（单位：m）Fig.7 Geometric model(unit：m)

表5 模型参数取值Tab.5 Parameter values of the model

当采用改进隐式算法进行多单元数值计算时，在第二个分析步的最后一个增量步可以得到如图8所示的位移结果，而采用传统隐式算法时在第二个分析步的第一个增量步出现了不收敛现象。为明确不收敛的原因，对计算过程进行实时监控，发现第一个增量步中的传统隐式算法无法对部分材料点的状态变量进行准确且有效的更新，导致整体计算出现不收敛。由此可以表明，与传统隐式算法相比，改进隐式算法不仅适用于简单的单单元计算，还可以用于复杂的多单元分析，对于高度非线性的弹塑性本构模型，改进隐式算法显然比传统隐式算法更加可靠、有效。

图8 地表沉降计算结果Fig.8 Calculation results of surface settlement

5 结论

（1）改进隐式算法和传统隐式算法的计算精度基本相同，但改进隐式算法的收敛性和整体计算效率比传统隐式算法要高很多。

（2）改进隐式算法可以高效地解决传统隐式算法所存在的不收敛和Jacobian矩阵奇异问题。

作者贡献声明:

乐 云：分析当前研究现状，指导研究方向，审查研究内容和结果的合理性。

雪克来提·亥依热特：负责具体的研究工作，收集并分析案例，组织验证实验，整理论文思路并撰写论文。

李永奎：提供研究背景和主要研究方法。

虞 涛：提供案例，组织实验。