一类新混合−似变分不等式解的存在性和唯一性
李 舜,谢祥俊
(1.成都工业学院,四川 成都 611730;2.西南石油大学理学院,四川 成都 610500)
许多学者[1− 4]之前研究过变分不等式解的存在、唯一性问题。本文在文献[5 − 7]的基础上,引入τ−η−g−余强制与ξ −η−g−松弛Lipschitz 连续概念,利用不动点技巧,研究了一类新混合−似变分不等式,证明了这类不等式解的存在、唯一性,此结果推广和发展了近期这方面的一些研究成果[5−7]。
1 预备知识
设X是自反Banach 空间,X•为其共轭空间,‖·‖表示X中的范数,〈·,·〉表示X•与X的配对,K⊂X为非空闭凸子集,映射T,A:K→X•,g:K→K,η:K×K→X,b:K×K→R=R∪{+∞}且满足:
(a)b(·,·)关于第一变元是线性的;
(b)b(·,·)关于第二变元是凸下半连续的;
(c)存在常数γ >0,使得b(x,y)≤γ‖x‖·‖y‖;
(d)b(x,y)−b(x,z)≤b(x,y−z),∀x,y,z∈K;
f:X×X→R且满足:存在常数α >0,β >0,使∀x,y∈X有
显然α ≤β。本文讨论如下混合−似变分不等式问题:对给定的ϖ ∈X•,求∈K,使

当g=I(恒等映射),f=0,问题(3)变为文献[5]讨论过的问题;当ϖ=−ϖ1,g=I,f=0,b(x,y)=q(y),这里q:,问题(3)变为文献[6]讨论过的问题;当T=0,ϖ=0,g=I,问题(3)变为文献[7]讨论过的问题,这里所讨论的问题是一个比前面讨论的问题更广泛的问题。
设T:K→X•,g:K→K,η:K×K→X为3 个映射。
定义:1)称T是τ−η−g−余强制的,若存在常数τ >0,使:
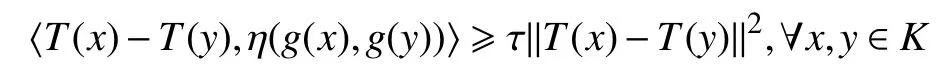
特别地,若g=I,则概念回到文献[5]中的τ−η余强制概念。
2)称T是ξ −η−g−松弛Lipschitz连续的,若存在常数ξ >0,使:

特别地,若g=I时,则概念回到文献[5]中的ξ −η−松弛Lipschitz连续。
2 主要结论
定理:设K⊂X为非空闭凸子集。映射T,A:K→X•,g:K→K,η:K×K→X,b:K×K→:K×K→且满足:如果
1)T关于η是 τ−η−g−余强制的,T是c−扩张映象,A是ξ −η−g−松弛Lipschitz连续的,并且T,A都是弱拓扑到强拓扑的连续映射。
2)η(x,y)=−η(y,x),∀x,y∈K, η是δ−Lipschitz 连续(见文献[8]定义2.1),A-T和η关于ϖ ∈X•有 0−g对角凹关系(见文献[8]定义2.3),且对固定的是从弱拓扑到强拓扑的连续映射。
3)b(·,·)满足(a)~(d),f(·,·)是双连续、双线性函数,且满足式(1)、式(2)。
4)g是线性、l−Lipschitz连 续映射;并且γ·l2<τ·c2+α−ξ·l2则问题(3)存在唯一解。
证明任意固定∈K,定义函数φ:K×K→∀x,y∈K,

因g是连续映射,对固定的是从弱拓扑到强拓扑的连续映射,从而对固定的是从弱拓扑到强拓扑的连续映射,加之T,A都是连续映射,故由文献[9]可知对固定的是连续的;b(·,·)满足(c)、(d),易得

即b(·,·)关于第二变元连续,再加上g连续,所以关于x∈K连续;f(·,·)关于两变元连续。这样对固定的y∈K,ϕ(y,x)在K上是连续的,即文献[8]引理2.1 的条件(i)满足。


同样在式(7)中令y=x2,在式(8)中令y=x1,而后再相加得:


