一种分析逻辑法性能的新方法及其应用
丁 春,张 静,匡华星,张玉涛
(1. 中国船舶集团有限公司第八研究院,南京 211153;2. 91033部队,山东 青岛 266000)
0 引 言
逻辑法及各种改进的逻辑法在雷达目标自动起始中得到了广泛的应用[1-5],国内外不少学者对其性能进行了分析[6-8]。文献[6]将逻辑法中移动滑窗的过程用马尔科夫状态转移的方法进行建模,使用Z变换推导出了窗口长度不超过4的各周期起始概率和平均起始周期数及标准差。文献[7]中通过人工枚举马尔科夫状态并利用计算机仿真马尔科夫状态转移的过程,计算出了窗口长度不超过4的各周期起始概率和平均起始周期数及标准差。文献[8]中在此基础上根据信噪比与检测概率的关系计算了航迹起始概率与信噪比的关系。
海面目标由于运动速度较慢,为了降低虚假起始的概率,往往需要较长时间的积累,如窗口长度n需要设计为7、9、12等。此时,利用Z变换的方法进行推导,或者人工枚举2n个状态是极其繁琐并且容易出错的事情。
本文将逻辑法滑窗检测的过程转化为二叉树[9]模型生成马尔科夫状态,并利用计算机仿真马尔科夫状态转移的过程,获得了各周期起始概率和平均起始周期数及标准差,为分析逻辑法起始性能提供了一种新的方法。
1 逻辑法的二叉树模型
序列(z(1),z(2),…,z(n))表示含有连续n次关联事件的窗口,各关联事件是相互独立的。如果关联到点迹,元素z(i)取值为1,反之为0。 当窗口中1的个数不小于m时便可宣布发现新的航迹,否则窗口向右滑动一次。
对于长度为n的窗口,窗口中共有2n个事件组合。窗口向右滑动的过程就是丢弃左侧的事件z(1)、增加事件z(n+1)的过程。
在二叉树中,每个结点存储窗口中的n个事件。左子树的根结点定义为“z(n+1)=0”,右子树的根结点定义为“z(n+1)=1”,函数f()定义为“产生窗口中的n个事件”,根结点有效定义为“根结点窗口中的n个事件未产生过或者已产生窗口事件组合数小于2n”。
在逻辑法的二叉树模型中,不存在二叉树的实体,构造二叉树的过程即产生了所有的2n个事件组合窗口。以长度为2的窗口为例说明采用先根方法产生的二叉树结构,如图1所示。图1中结点上的序号(1)~(7)表示结点产生的顺序,以浅黑色填充的结点表示该结点无效。
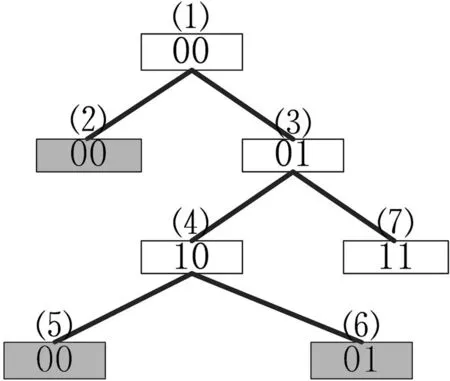
图1 窗口长度为3的逻辑法二叉树
(1) 根结点设为(0,0)。
(2) 窗口向右移动,丢弃左侧的事件z(1)=0,增加事件z(n+1)取值为0。 根据前述定义,z(n+1)=0的窗口(0,0)已作为根结点,所以结点(0,0)的左子树无效,即没有左子树,在图2中以浅黑色填充的结点表示。
(3) 对于根结点(0,0),再产生右子树。窗口向右滑动,丢弃左侧的事件z(1)=0,增加事件z(n+1)取值为1。根据前述定义,z(n+1)=1的窗口(0,1)未产生过,作为右子树的根结点。
(4) 对于结点(0,1),先产生左子树。窗口向右滑动,丢弃左侧的事件z(1)=0,增加事件z(n+1)取值为0。根据前述定义,z(n+1)=0的窗口(1,0)未产生过,作为左子树的根结点。
(5) 对于结点(1,0),先产生左子树。窗口向左滑动,丢弃左侧的事件z(1)=0,增加事件z(n+1)取值为0。根据前述定义,z(n+1)=0的窗口(0,0)已产生过,所以结点(1,0)的左子树无效,即没有左子树。
(6) 对于结点(1,0),再产生右子树。窗口向右滑动,丢弃左侧的事件z(1)=0,增加事件z(n+1)取值为1。根据前述定义,z(n+1)=1的窗口(0,1)已产生过,所以结点(1,0)的右子树无效,即没有右子树。
(7) 对于结点(0,1),再产生右子树。窗口向右滑动,丢弃左侧的事件z(1)=0,增加事件z(n+1)取值为1。根据前述定义,z(n+1)=1的窗口(1,1)未产生过,作为右子树的根结点。至此,长度为2的窗口共22=4个事件组合生成完毕。
2 性能分析方法
分析逻辑法性能的问题可以抽象为[7]:对于n个相继发生的事件,每个事件成功概率为p且相互独立,则可以求出在第N次事件发生时获得m次成功的概率。对于已经产生的2n个事件组合窗口,可以看作具有有限的状态数目和恒定的转移概率的离散马尔科夫过程。
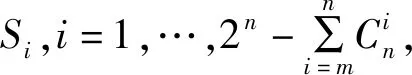
假设初始状态为S1,窗口向右滑动的过程就是以概率p选择z(n+1)=1,或者以概率q=1-p选择z(n+1)=0,达到新的状态的过程。
定义概率向量PN=(PN(1),PN(2),…,PN(Q))T,其中每个元素表示第N次事件发生时对应状态的概率。特别地,PN(Q)表示事件成功数量大于或等于m的概率。初始概率向量P0=(1,0,…,0)T。
定义状态转移概率矩阵T=(Tij)′Q×Q,其中Tij表示第i个状态转移为第j个状态的概率。

3 性能比较与计算


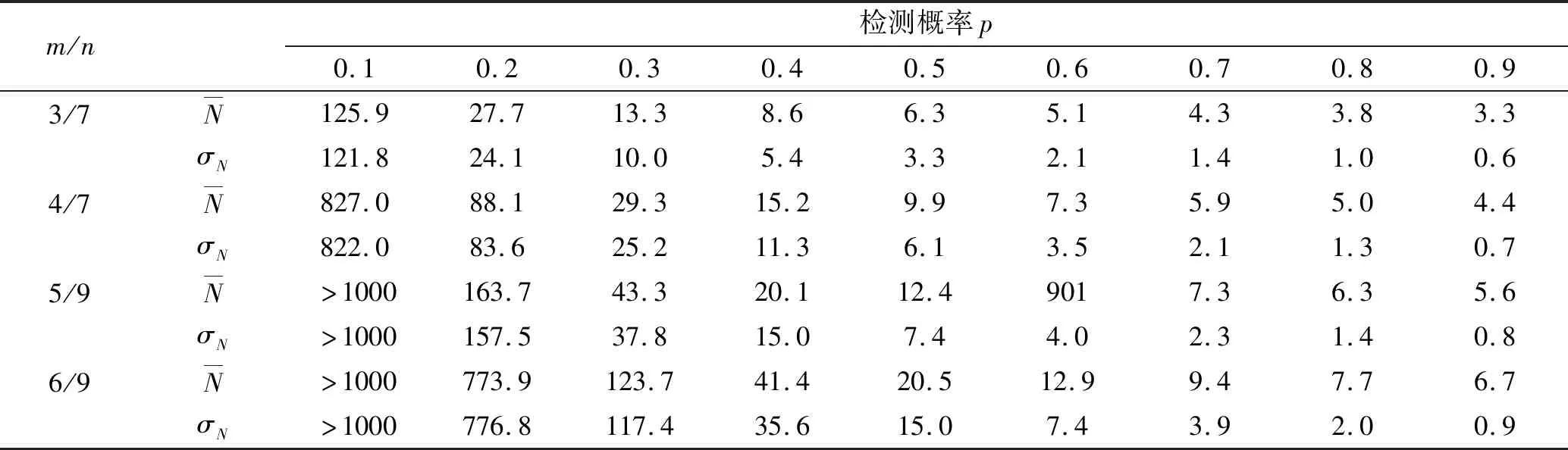
表1 航迹起始的平均扫描周期数和标准差
4 结束语
本文将逻辑法滑窗的过程抽象为二叉树模型。对于任意长度窗口,按照递归的先根遍历二叉树的方法产生了所有的事件组合窗口。利用马尔科夫过程转换,计算了常用的3/7、4/7、5/9、6/9逻辑的各扫描周期航迹起始的概率、航迹起始所需的扫描周期数的平均值和标准差。根据本文的模型,可以计算出更长窗口逻辑法的各扫描周期航迹起始的概率、航迹起始所需的扫描周期数的平均值和标准差。本方法可方便地拓展到对更长窗口长度的逻辑法起始性能进行分析。

