T型刚构转体施工状态风致响应的风洞试验研究
孔令总 王泽文 何向东
针对转体施工的某T型刚构桥梁,文章介绍通过大比例尺气弹模型风洞试验,测试了其最大双悬臂状态下最大位移和球铰截面处的风致内力。研究结果可为施工期抗风设计提供数据支撑。
T型刚构; 转体施工; 气弹模型; 风载内力; 风洞试验
U448.23+1 A
[定稿日期]2020-12-24
[作者简介]孔令总(1988~),男,硕士,工程师,研究方向为道路与铁道工程。
随着城际公、铁交通路网的大力建设与发展,越来越多的城际公路桥的设计与建造,面临着多车道、需跨越既有公、铁线路且不能影响其正常运营的挑战,肇始于20世纪40年代的桥梁转体施工工艺,由此在连续梁及T型刚构得到大力推广与应用。目前国内采用转体施工的T型刚构,最大重量已近5×104 t。尽管转体施工的时长大约仅在1 h左右,但随着转体施工T型刚构主墩与主梁的高度、及主梁宽度等的增大以及薄壁钢箱梁的相对质量与阻尼的减小,使得在风环境较为严峻地区进行转体施工的T型刚构,必须对其风致响应详加考察,以确保转体施工的安全。
球铰是传递结构上、下部荷载的关键部位,在风敏感区,转体施工时必需明确记及风荷载的、球铰处截面的内力变化。见诸报道的对于转体施工的T型刚构等的风致响应研究方法,主要依赖于人工模擬的脉动风场,以及由Fluent数值模拟的主梁及墩的静风系数,采用Ansys对其静风或抖振响应进行计算分析[1-4],或采用Ansys的接触分析,研究球铰面的风致响应[5-6],得出球铰接触面或上转盘混凝土局部应力超标的极限风速。显然,以上分析计算所需的基本系数均基于规范[7]或数值风洞的模拟结果,难以精确考察风偏角、攻角的影响。
本文利用转体施工T构的气弹模型,在均匀流场、通过非接触式激光位移计与安装于墩底的高频底座天平,直接测出不同风速及风偏角下T构悬臂端的位移及墩底内力。所得结果可与计算分析模型相校核,可为分析模型精确化的改进提供试验依据。
1 工程背景
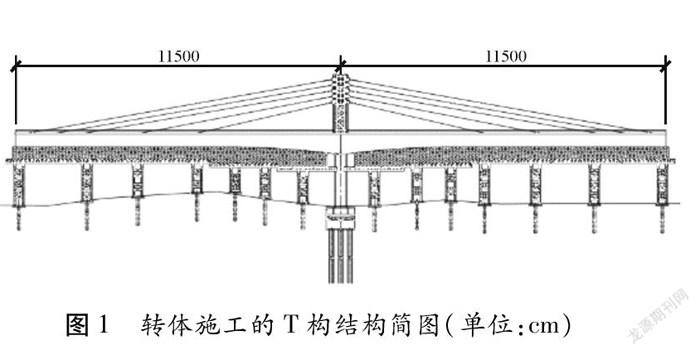
方案桥系采用转体施工、双幅并列的城际跨越既有线路的一座公路桥,本文以其右幅T构转体施工最大双悬臂状态为研究对象,主梁为单箱三室钢箱梁,梁宽约49.2 m,桥面高度约27.3 m,跨度达120 m,特设临时塔架及斜拉索,以确保转体施工的顺利进行。转体施工前的T构及临时塔架、斜拉索等,如图1所示。
根据桥址位置及具体地貌,参照文献[7],将其设计基本风速确定为U10=36.6 m/s,地表类别为B类。由此得其施工状态的桥梁设计基准风速为:Usd=39.7 m/s。
2 结构动力特性分析
采用Ansys进行T构最大双悬臂状态的结构动力特性分析时,其主梁和主墩均采用空间梁单元模拟,塔架及斜拉索则采用空间杆单元模拟,其中斜拉索为仅受拉的空间杆单元,并由索的初始张力换算而得的初应变,考虑斜拉索初始张力对结构动力特性分析的影响。T构施工态的有限元模型如图2所示。
T构最大双悬臂状态的前6阶模态频率及振型特征见表1。由表1可见,T构最大双悬臂状态的基本振型以主梁竖摆、横摆及对称竖弯为主。主梁第一对称横弯及对称扭转的频率均已较高。
3 气弹模型均匀流试验及结果
T构最大双悬臂施工状态的气弹模型设计,采用了1∶40的几何缩尺比,相应的风速比为1∶400.5,频率比为400.5∶1。试验在XNJD-3工业风洞中进行,该风洞是目前世界最大的直流式、边界层风洞(指适用于土木工程、环境工程等风洞试验的工业风洞)。其试验段尺寸为22.5 m(宽)×4.5 m(高)×36.0 m(长);试验风速范围为1.0~16.5 m/s。
在进行均匀流场风洞试验前,首先采用自由振动衰减法完成气弹模型的模态测试。T构最大双悬臂状态气弹模型的模态测试结果见表2。表2表明T构最大双悬臂状态气弹模型的动力特性达到了文献[7]的各项要求。
考虑到桥梁变截面、桥面横、顺桥向坡度的影响,为详细考察不同风偏角下、T构最大双悬臂状态气弹模型在均匀流场下的风致响应,特设置了如图3所定义的8个不同风偏角。试验时,T构最大双悬臂状态气弹模型较高悬臂端(与图中Y1墩顶相对应)的竖向及横桥向位移,均由KEYENCE非接触式IL-1000(Intelligent Laser Sensor)激光位移传感器测量。
墩底内力采用的9105-NET-OMEGA191-IP68的ATI多轴力与力矩(6分量),如图4所示。安装于墩底截面的天平测试结果已经调整为:Fx与桥轴(即结构坐标系的OX轴)平行,Fz与横桥向(即结构坐标系的OZ轴)平行,Fy则与竖直向平行(即结构坐标系的OY轴),三轴彼此正交,并符合右手螺旋法则。其Tx、Ty与Tz分别为绕各自力轴的弯矩,其中Tx、Tz分别为面外及面内弯矩,而Ty即扭转力矩。
由于转体施工状态与成桥状态的体系转换,气弹模型支座系以成桥状态的墩底高度为设计基准,测力天平也安装于此墩底截面,而在转体施工时,T构上部结构的重量及所受风荷载,均由球铰面承受。故,由试验所测得的墩底截面内力,尚需根据力的平移法则,换算至球铰中心处截面(图5)。
图7给出了8个不同风偏角下、主梁悬臂端竖向及横桥向位移的最大单边振幅随风速的变化。该图表明,在此状态下,悬臂端位移以竖向为主,且以在正交风作用时响应最大。由于桥面横桥向坡度的影响,竖向位移随风速的变化规律,对于风偏角而言,仅保持趋势的一致,而非完全对称。
图8~图10分别给出了在不同风偏角下、墩底截面(已换算至球铰中心处截面)三个轴向内力Fx、Tx,Fy、Ty,Fz、Tz随风速的变化。
文献[3]所计算分析的T构,其结构特征、尺度等与本文研究对象大致相同,对比其墩底内力(力矩)计算结果,与以上正交风作用时、相同风速下的测试结果大体相当。验证了利用高频底座天平直接测试转体施工的T构墩底风载内力的可行性与可靠性。
4 结束语
对于转体施工的T构。其球铰是转体施工时承担上部结构重量的主要载体。随着材料与施工技术的进步,转体施工的T构,主墩渐高,主梁也日益更宽、更高、更长,其质量及阻尼相对减小,在风敏感区进行转体施工时,有必要考虑风致振动对球铰截面内力的影响。利用高频底座天平,进行T构转体施工最大双悬臂状态气弹模型风洞测力试验,可简便、有效地获得此时球铰中心处截面的风载内力,既可为大型T构的转体施工提供验算根据,也可为相应的理论计算、分析模型提供必要的参考、校订依据。
参考文献
[1] 翟鹏程. 转体梁施工中的不平衡问题及风致振动研究[D].北京: 北京交通大学, 2008.
[2] 黄伟文. 转体施工T形刚构桥抗风性能研究[D].武汉:武汉理工大学,2014.
[3] 瞿景东. 风致动力效应对T构桥梁转体施工的影响研究[D].重庆:重庆交通大学,2018.
[4] 秦少宗. 跨铁路线斜拉桥转体施工监控技术研究[D].石家庄:石家庄铁道大学,2019.
[5] 王坤. T型悬臂梁平转施工关键技术的研究[D].天津:天津大学,2011.
[6] 左敏. 连续梁桥平转施工控制关键技术研究[D]. 南京:解放军理工大学,2016.
[7] JTG/T 3360-01-2018 公路桥梁抗风设计规范[S].
1326500520335

