动点轨迹为直线的模型

胡海友

基本模型：形状不变的三角形（△ABC），有一个顶点（A）固定不动，如果第二个顶点B在一条定直线上运动，那么第三个顶点C必在一条定直线上运动.以这一模型为背景的动点问题是中考常见题型，下面以中考题为例简析解此类题的关键.

一、认识模型，找寻方法

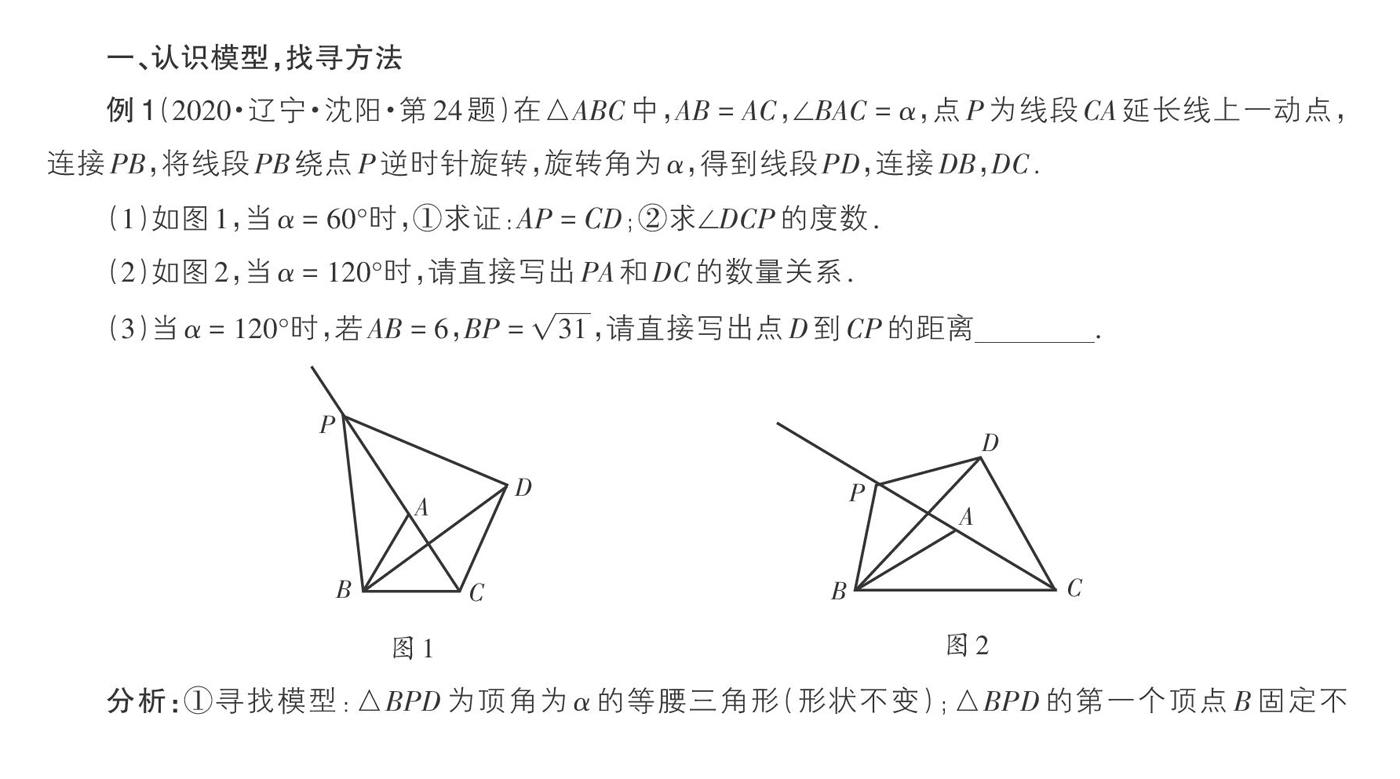
例1（2020·辽宁·沈阳·第24题）在△ABC中，AB = AC，∠BAC = α，点P为线段CA延长线上一动点，连接PB，将线段PB绕点P逆时针旋转，旋转角为α，得到线段PD，连接DB，DC.

（1）如图1，当α = 60°时，①求证：AP = CD;②求∠DCP的度数.

（2）如图2，当α = 120°时，请直接写出PA和DC的数量关系.

（3）当α = 120°时，若AB = 6，BP = [31]，请直接写出点D到CP的距离 .

[P][D][B][C][A][图1] [D][P][A][C][B][图2]

分析：①寻找模型：△BPD为顶角为α的等腰三角形（形状不变）;△BPD的第一个顶点B固定不动，第二个顶点P在直线AC上，则第三个顶点必在一条定直线上.

②证明思路：先找到△BPD的一个特殊位置△ABC（点P与点A重合），然后证明△PBA和△DBC全等或相似，得到∠BCD = ∠BAP = 180° - α，所以∠BCD为定角，又因为CB为定边，可得CD为定直线，所以点D在定直线CD上运动.

解：（1）易得图1中△ABC和△BPD都是等边三角形，可证△PBA ≌△DBC（SAS），得AP = CD，∠BCD = ∠BAP = 120°，所以∠DCP = ∠BCD - ∠ACB = 120° - 60° = 60°.

（2）图2中的△ABC可以看作是△BPD的一个特殊位置（点P与点A重合），符合上面模型，先证△ABC ∽△PBD，可得[BPBD] = [ABBC]，可证得∠PBA = ∠DBC，进而证得△PBA∽△DBC（两边成比例且夹角相等），得[CDAP] = [BCBA] = [3]，∠BCD = ∠BAP = 60°，所以∠PCD = ∠BCD - ∠ACB = 60° - 30° = 30°.

（3）如图3，△CBP中，已知两边和一角，即BC = [3AB] = 6[3]，BP = [31]，∠BCP = 30°，过点B作BN⊥CP交直线CP于N. 即可求出AP = 1或5，再由第（2）问中的[CDPA] = [3]可求得CD = [3]或5[3];过点D作DM⊥PC于M，由前面结论∠PCD = 30°可求得DM = [32]或[532] .

二、强化模型，拓展提升

例2（2020·湖北·襄陽·第24题）在△ABC中，[∠BAC=90°]，[AB=AC].点D在边[BC]上，[DE⊥DA]且[DE=DA]，[AE]交边[BC]于点[F]，连接[CE].

（1）特例发现：如图4，当[AD=AF]时，①求证：[BD=CF];②[∠ACE=] °.

（2）探究证明：如图5，当[AD≠AF]时，[∠ACE]的度数是否为定值，并说明理由.

（3）拓展运用：如图6，在（2）的条件下，当[EFAF=13]时，过点[D]作[AE]的垂线，交[AE]于点[P]，交[AC]于点[K]，若[CK=163]，求[DF]的长.

（4）变式训练：若AC = 6[2]，连接BE，当AE + BE有最小值时，DF = .

[A][B][D][F][E][C] [A][B][D][F][E][C] [A][B][D][F][E][C] [P][K][图5][图4][图6]

解析：（1）特殊情况下易证BD = CF，[∠ACE=] 90°;也可以与下面（2）问证法相同.

（2）①图5中△ADE为∠ADE = 90°，∠DAE = 45°的等腰直角三角形，形状不变;

②△ADE的第一个顶点A固定不动，第二个顶点D在直线BC上运动，则第三个顶点必在一条定直线上运动;

③如图7，过点A作AM⊥BC于点M，可证△AMC也是等腰直角三角形，△AMC可以看作是△ADE的一个特殊位置（点D与点M重合），先证△ADE ∽△AMC，可得[ADAM] = [AEAC]，即[ADAE] = [AMAC]，再证得∠DAM = ∠EAC，可证△DAM ∽△EAC，得∠ACE = ∠AMD = 90°;

④由于∠ACE的顶点C不动，一边CA不动，角度不变为90°，可以确定另一边CE为定直线，所以点E在过点C且垂直于CA的定直线上运动.

（3）如图7，由第（2）问中的∠ACE = 90°以及∠BAC = 90°，可证AB[⫽]CE，则△ABF ∽△ECF，

∴[CEAB] = [CFBF] = [EFAF] = [13]，可得AB = 3CE，即AC = 3CE，

设CE = a，则AB = AC = 3a，

由CK = [163]得AK = AC - CK = 3a - [163]，

可证DK垂直平分AE，则KE = AK = 3a - [163]，

在Rt△CEK中，由勾股定理得[EK2] = [CK2] + [CE2]，[可]得a = 4，则CE = 4，AC = 12，

则AE = [AC2+CE2] = 4[10]，则DP = [12]AE = 2[10]，

由[EFAF] = [13]，[PE] = AP = [12]AE，可得PF = [12]PE = [14]AE = [10]，

在Rt△DPF中，DF = [DP2+PF2] = 5[2].

[图7][A][K][C][P][M][F][E][B][D] [A][C][F][E][D][A'][F'][图8][B]

（4）如图8，因为点E在垂直于AC的直线上运动，故本题属于“将军饮马”问题，作点A关于CE的对称点A'，连接A'B，当点E在A'B上时，AE + BE最小，且最小值为线段A'B的长.

可证△A'CE ∽△A'AB，得[CEAB] = [A'CA'A] = [12]，再证△FCE ∽△FBA，则[CFBF] = [CEAB] = [12]，可得[CFBC] = [13].

∴CF = [13]BC = [13] ×[ 2]AC = [13] ×[ 2] × 6[2] = 4，BF = 8，

将△ACF绕点A顺时针旋转90°得△ABF'，再证△ADF ≌△ADF'，得BF' = CF，DF' = DF;

在Rt△DBF'中，由勾股定理得[F'D2] = [BD2] + [F'B2]，即[DF2] = [BD2] + [CF2]，

即[DF2] = [（8-DF）2] + [42]，解得DF = 5.

综上所述，通过实例认识模型，可为以后研究定点到动点的最小距离做好铺垫.

（作者单位：沈阳市第一二六中学）