大型稀疏线性代数方程组的通用性迭代解法
廖晓花
(闽南理工学院 信息管理学院,福建 石狮 362700)
现如今大型稀疏线性代数方程组已经被广泛应用在随机线性控制系统中,但由于难以得到方程组的最优解,将其应用至随机线性控制系统后,难以实现系统的精准控制,导致系统控制效果变差.为解决该问题,需要深入研究大型稀疏线性代数方程组的通用性迭代解法[1].大型稀疏线性代数方程组的求解传统方法主要有梯度搜索方法、线性组合控制方法、最大似然估计方法和二次规划算法等[2],通过构造大型稀疏线性代数方程组的组合控制模型,结合收敛性和稳定性判断方法,实现大型稀疏线性代数方程组求解[3].但传统方法进行大型稀疏线性代数方程组解析的自适应性不好,二次规划能力不强,导致系统控制效果差.
针对上述问题,本文通过复变函数分析方法得到大型稀疏线性代数方程组的解特征向量,结合Schur收敛性判断和随机线性组合控制方法,进行方程组的通用性迭代寻优,结合最小熵估计的方法获取大型稀疏线性代数方程组的通用性迭代解.
1 方程组重构和解特征向量分析
构建大型稀疏线性代数方程组的凸优化组合模型,在此基础上计算大型稀疏线性代数方程组的解特征向量.
1.1 大型稀疏线性代数方程组重构
本文采用基函数分析方法[4]获取大型稀疏线性代数方程组的特征函数,表示为d1(t)和d2(t),满足
(1)
(2)
其中,h1,h2,τ1与τ2为大型稀疏线性代数方程组的正交特征量[5].
在获取方程组特征函数的基础上,计算大型稀疏线性代数方程组的规范特征解[6]
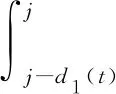
(3)
其中,xi(t)与wji(t)分别表示不同的方程组特征函数.
通过时滞判断方法,结合时延特征量d(t),得到大型稀疏线性代数方程组的最大信息熵[7]
(4)
采用最大信息熵泛函,得到大型稀疏线性代数方程组的稳态控制参数模型
(5)
其中,A、B表示不同的方程组控制参数,S表示最大信息熵.
在有界稳定性条件下[8],构建大型稀疏线性代数方程组的点积函数Gm(s),在时滞环节e-tms中进行时延控制[9],结合全稳态跟踪融合模型GC(s),构建大型稀疏线性代数方程组的凸优化组合模型
R(s)+Y(s)=1-Gm(s)[e-tms+GC(s)]2.
(6)
通过构建大型稀疏线性代数方程组的凸优化组合模型,进行大型稀疏线性代数方程组重构.
1.2 解特征向量分析
通过上述处理过程进行方程组重构之后,采用稳定性判断方法,计算描述性统计特征量[10],结果为
(7)
和
(8)
其中,Ψ(d1(t),d2(t))=Ψ+Ψ1(d1(t))+Ψ2(d2(t)),当Ψ(d1(t),d2(t))<0时,则存在
(9)
在方程组的解稀疏有界条件下,根据方程组的描述性统计特征量,得到大型稀疏线性代数方程组的随机泛函加权特征量
(10)
其中,F(x)表示解稀疏有界条件,E表示稀疏参数,e与eT分别表示不同的稀疏矩阵参数.
基于扰动特征分析方法[11],结合随机泛函加权特征量,计算上述方程组的扰动特征函数
(11)
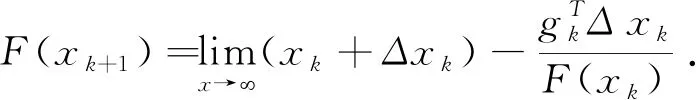
令
Δxk=αpk,
(12)
其中,α为大型稀疏线性代数方程组解向量的偏值向量[12],pk为大型稀疏线性代数方程组的模糊数度函数,当输入向量F(xk+1) (13) 当pk=-gk时,F(xk+1)表示为大型稀疏线性代数方程组的临时约束解 通过对大型稀疏线性代数方程组重构,并进行了解特征向量分析,根据有界向量融合进行特征解优化求解. 进行大型稀疏线性代数方程组的通用迭代控制和闭环分析,建立大型稀疏线性代数方程组的线性无关组,在此基础上进行大型稀疏线性代数方程组的通用性迭代寻优,以提高大型稀疏线性代数方程组的自适应迭代和收敛判断能力[13]. 采用自适应学习方法,得到大型稀疏线性代数方程组的最大迭代解寻优模型 (14) 其中,∂为学习速率. 基于上述解特征向量分析,结合最大迭代解寻优模型,构建通用迭代控制的特征辨识模型 (15) 在该模型中,xT(t)与xT(s)分别表示最大迭代解寻优模型及最小和最大迭代解寻优模型.通过均衡控制和有界约束的方法[14],结合特征辨识模型得到期望均衡控制模型 根据上述分析,进行稀疏线性代数方程组的通用性迭代解中的关于线性无关组分析,在此基础上进行大型稀疏线性代数方程组的通用性迭代寻优[15]. 结合上述通用性迭代解线性无关组,得到大型稀疏线性代数方程组的通用性迭代解的Schur收敛性条件 (16) 结合Schur收敛性判断条件和随机线性组合控制方法,进行大型稀疏线性代数方程组的收敛性证明,结合最小熵估计方法得到凸组合模型 (17) 基于上述扰动特征方程组,结合凸组合模型,得到通用性迭代解的最小二乘估计结果 (18) 定理1大型稀疏线性代数方程组通用解具有渐近稳定性. (19) 在此基础上进行大型稀疏线性代数方程组的通用性迭代解的二乘估计,得到模型的渐进稳定解∃X(k)>X(0),使得 (20) 因为当N→时,|X(k)|→0,得到大型稀疏线性代数方程组的渐近稳定性特征方程,此时‖W(X(k))‖→0,通过扰动方程,得到渐近寻优解为 (21) (22) 当判别函数F′(X)满足W(F(X))≤LW(X),L是常数,结合方程组的通用迭代解,得到优化控制矩阵 (23) (24) 根据上述分析,得到大型稀疏线性代数方程组的通用性迭代解的收敛有界. 为准确得到大型稀疏线性代数方程组的通用迭代解,进行大型稀疏线性代数方程组的通用迭代解方法分析.通过构建大型稀疏线性代数方程组的收敛性判断和寻优控制模型,结合最小熵估计方法实现大型稀疏线性代数方程组的通用性迭代解的优化求解.2 方程组通用迭代解分析
2.1 线性无关组分析

2.2 收敛性证明
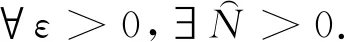
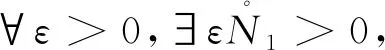
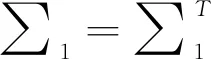
3 结语

