滚仰式半捷联导引头制导信息提取技术研究

秦思凯，李 超，任宏光，胡一帆，张跃坤

(1 中国空空导弹研究院，河南洛阳 471009；2 陆装驻洛阳地区航空军代室，河南洛阳 471009)

0 引言

滚仰式捷联导引头具有体积小，重量轻，成本低的优势，符合现代空空导弹的发展要求，近年来成为研究的热点[1-2]。国内外针对滚仰式导引头平台稳定原理开展了诸多研究，刘慧等研究了稳定平台运动学和动力学模型，给出了平台驱动力矩的计算方法[3]；花文涛对滚仰内外框动力学进行了分析，给出了电机指令的解算方法[4]；肖仁鑫等对内外框架进行了系统建模，并完成了稳定和跟踪回路的仿真[5]。由于平台上没有惯性测角器件，无法直接获得惯性视线角速率，如何提取制导信息是制导系统闭合的关键。通过重构视线角速度的方式可以得到惯性视线角速度[5-6]，由弹体姿态角速率、失调角、框架滚仰角等信息解算出惯性系下的视线角再选择合适的跟踪微分器，也可提取出惯性系下的视线角速率[7-14]。江云等提出一种利用导引头提供的失调角、框架角及框架角速度等信息构建“虚拟偏仰式导引头”的方法，设计Kalman 滤波器对目标垂直视线运动信息进行估计，进而间接提取出视线角速度信息，用于产生制导指令[15]。为了克服传感器精度和微分运算不理想所造成的视线角速度计算精度不足，贾筱媛给出了一种基于导弹-目标角跟踪模型的目标视线角速度滤波模型，能有效提取视线角速率[16]。以上研究中，视线角速度重构方法存在外环转速高时提取信息抖动的问题，微分方法则存在放大测量误差的问题。文中就视线角速率提取问题开展研究，提出一种采用扩展卡尔曼滤波方法提取视线角速率的方案。

1 滚仰式捷联导引头稳定平台数学模型

首先建立导引头相对于弹体运动的动力学模型，TR为平台控制力矩，R代表外框坐标系，则有：

TR=[TRxTRyTRz]T

(1)

(2)

式中γS为导引头滚转框架角。外环转动惯量在外环坐标系的投影为：

(3)

内环转动惯量在外环坐标系的投影为：

(4)

外环转动角速度在外环坐标系的投影为：

(5)

内环转动角速度在外环坐标系的投影为：

(6)

式中，ϑS为导引头俯仰框架角。则有平台角动量在外环坐标系投影为：

(7)

内环角动量在外环坐标系投影为：

(8)

由角动量定理可得：

(9)

为了简化模型，在导引头稳定平台配平情况下，内框连同光电负载在内框坐标系的惯量积近似等于0。则有内框在外框坐标系xRyRzR的转动惯量及其导数为：

(10)

(11)

则有导引头相对于弹体运动的动力学模型为：

(12)

(13)

其中：

假设力矩电机的动力学模型为：

(14)

其中:bx,bz为常数增益;uγ,uθ为力矩电机的电流信号。加于力矩电机的电流信号用于驱动导引头保持平台稳定及目标跟踪。

2 惯性视线角速度的导出

视线相对于惯性空间的旋转角速度矢量为：

ωP=ωB+ωSB+ωPS

其中，ωB为弹体相对于惯性空间的旋转角速度矢量，在弹体系投影为：

(15)

ωSB为导引头坐标系相对于弹体坐标系的旋转角速度矢量，在弹体系下投影为：

(16)

ωPS为视线相对于导引头坐标系的旋转角速度矢量，在视线系下投影为：

(17)

视线相对于导引头坐标系的旋转角速度在弹体坐标系的投影为：

(18)

视线相对于惯性空间的旋转角速度在弹体坐标系的投影为：

在目标跟踪阶段，探测器误差角εz,εy都非常小，故假定sinε≈ε，cosε≈1，在稳定跟踪阶段，误差角εz,εy几乎接近于零，对视线旋转角速度的贡献可以忽略不计，故有惯性视线角速度在弹体系投影为：

(19)

3 采用扩展卡尔曼滤波技术估计框架角旋转角速度

惯性视线旋转角速度估计中，有效的测量数据有：导引头滚转框架角γS，俯仰框架角ϑS，弹体在惯性空间的旋转角速度p,q,r。导引头动力学模型如式(12)、式(13)所示，电机模型如式(14)、式(15)所示。

为了进一步简化模型，在滤波器的动力学模型中忽略弹体角加速度的影响，也即忽略p,q,r导数的影响。滤波器的参数为：

(20)

(21)

(22)

w=[0us0us]T,v(k)=[vϑvγ]T

由式(12)和式(13)可知，系统具有强烈的非线性，卡尔曼滤波方程适用于线性系统，在对非线性系统进行滤波时，可对状态方程进行线性化处理，即通过扩展卡尔曼滤波方法对非线性系统进行滤波 ，则有系统状态方程线性化后得到的状态方程：

(23)

系统干扰输入协方差矩阵为：

(24)

系统的状态转移矩阵为：

(25)

其中：

输入(控制)转移矩阵为：

(26)

(27)

对状态方程进行离散化，设采样间隔为Ts，则有离散状态转移矩阵：

(28)

离散化的系统干扰输入协方差矩阵：

(29)

离散化的输入(控制)转移矩阵有：

(30)

综上所述，则卡尔曼滤波公式为：

(31)

其中:Kk为滤波增益矩阵;Pk为滤波误差的协方差矩阵;Mk为预测误差的协方差矩阵。

在导引头跟踪目标阶段，因探测器上的目标误差较小，在实际中可近似把导引头光轴在惯性空间的旋转角速度代替视线在惯性空间的旋转角速度，作为导弹制导所需信号。根据上面建立的扩展卡尔曼滤波方程，即可解耦弹体运动对导引头运动的影响，从而估计出导引头框架角速度信号，结合弹体旋转角速度信号，得到光轴在惯性空间的旋转角速度。

4 仿真结果与分析

搭建导弹和目标完整的运动模型及动力学模型。导引头模型中，平台惯量、电感、电阻等参数选取某产品的典型参数，框架角测量和框架角速率的测量引入白噪声，以模拟真实的导引头工作状态。导弹飞行时，分别采用视线角速率重构和扩展卡尔曼滤波技术提取视线角速度，进行效果对比。导弹初始仿真条件如表1所示。

表1 仿真弹道条件

俯仰视线角速率输出结果分别如图1及图2所示，EKF代表扩展卡尔曼滤波方法，RC代表重构方法，真实弹目视线角速率图中记为los。从图中可以看出，真实的弹目视线角速率变化比较平滑，这是因为弹目接近速度较低，弹目视线角变化较慢。弹道初始阶段两种视线角速率提取方法的提取误差都较大，但提取误差快速收敛到一个较小的值。从图2局部放大图可以看出，采用视线角速率重构的提取方法由于测量信息的误差带来视线的较大抖动，表现出视线角速率提取信息波动较大。采用扩展卡尔曼滤波提取方法则可以较平滑的提取视线角速率信息，且跟真实弹目视线角速率误差保持在一个很小的范围内。

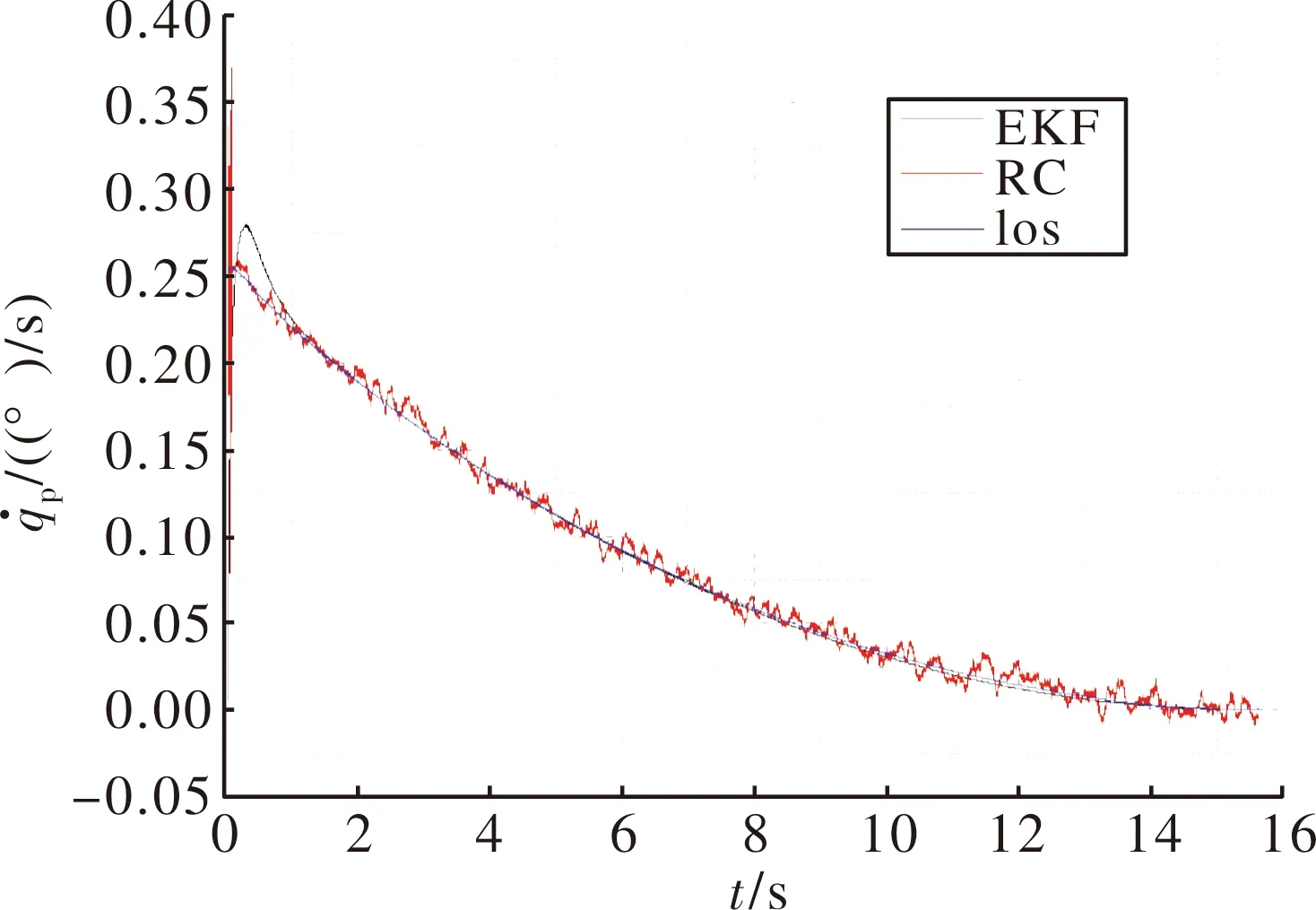
图1 俯仰视线角速率

图2 俯仰视线角速率局部放大图

偏航方向视线角速率提取如图3和图4所示。可以看出在视线角速率变化较大的情况下，采用扩展卡尔曼滤波方法提取视线角速率依然能保持良好的跟踪精度，相对视线角速率重构方法精度更高，曲线也更平滑。

图3 偏航视线角速率

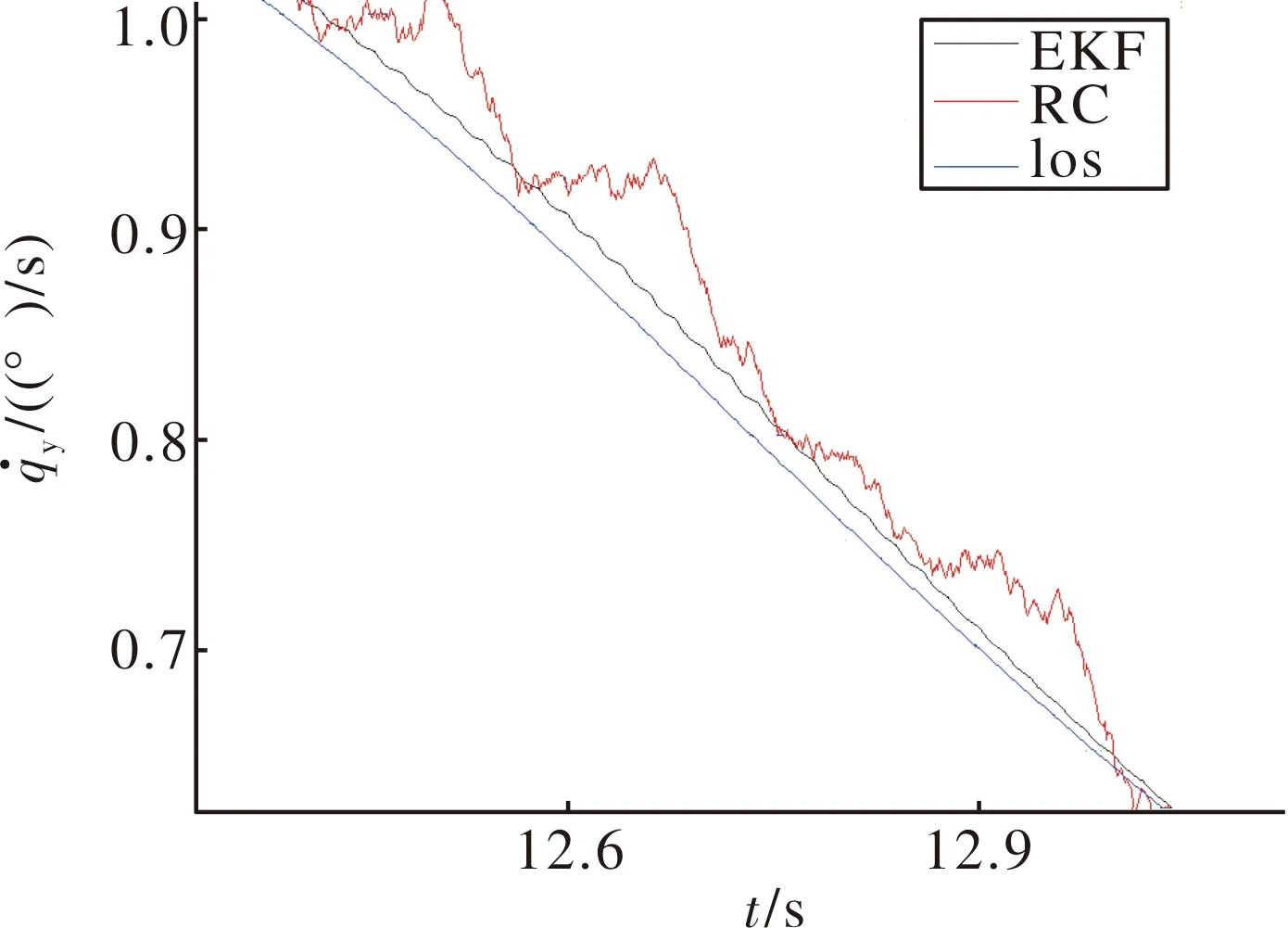
图4 偏航视线角速率局部放大图

某型导弹制导系统对导引头提出的制导信息提取精度指标为误差不超过0.04°/s，仿真结果表明，扩展卡尔曼滤波提取算法的精度满足该指标要求，在俯仰和偏航方向的误差精度均不超过0.025°/s，而视线角速率重构方法的最大误差达到了0.075°/s，无法满足制导精度指标要求。

5 结论

建立了滚仰式导引头平台动力学模型，并提出了用卡尔曼滤波方法进行制导信息提取的方案。仿真结果表明，采用扩展卡尔曼滤波技术间接提取视线角速度可以避免制导信息提取出现“抖动”的情况，经仿真验证，滤波提取的视线角速度精度较高，误差可控制在0.025°/s以内 ，能够满足制导精度要求，可以采用滤波输出的视线角速度闭合制导系统。