基于旅行商问题转化和遗传算法求解汽配件喷涂顺序

，*

（1.西华师范大学数学与信息学院，四川南充 637009；2.西华师范大学计算方法及应用软件研究所，四川南充 637009）

0 引言

汽车产业的飞速发展使得汽配件的生产呈现爆发性增长。外观类汽配件通常需要进行颜色喷涂，这样既能满足顾客对汽车外观的审美需求，也能确保汽车在自然环境条件下的耐用性需求。生产线上的汽配件喷涂颜色时，若前后相邻两个汽配件需要喷涂不同的面漆色，则称为一次“换色”，此时需要更换喷枪的涂料颜色，换色次数的多少会影响生产成本。

上述情形可称为汽配件颜色喷涂顺序问题，本文选取比较常见的一种环形喷涂生产线，如图1 所示，生产线上设置有一定数量的滑橇，有特定的换件处和喷涂处。汽配件被依次安装在滑橇上，随滑橇在轨道上移到喷涂处进行喷色，当移到换件处则将其取下。

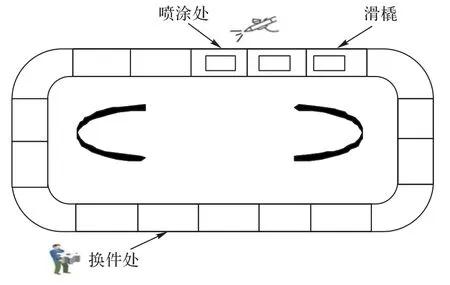
图1 汽配件喷涂生产线Fig.1 Spraying production line for auto parts

在实际生产过程中，某些类别的汽配件由于形状等因素会导致不能相邻排列、某些颜色的汽配件由于颜色原料的特定要求会导致不能相邻排列，这些因素都会影响到颜色切换次数进而影响到生产成本，因此，研究和优化一批生产任务内的汽配件序列，可以理论指导生产实践并帮助企业提高生产效率、降低生产成本。

上述问题实质上是一类产品加工顺序问题，也可看作是一类柔性作业车间调度问题。通常遇到这类调度问题首先考虑到用经典的动态规划方法来对问题进行求解，但动态规划方法在求解大规模问题时效率低、速度慢，而在对原问题的分析中发现在汽配件喷涂生产线上，每一个滑橇上安装的汽配件都要喷涂且只喷涂一次，这非常类似于旅行商问题（Travelling Salesman Problem，TSP）［1］，故本文采用借鉴TSP建模的方法对汽配件喷涂顺序问题进行转化建模。旅行商问题作为著名的NP-hard 问题，近年来许多专家学者对该问题的求解提供了许多的优化算法，如遗传算法［2-3］和模拟退火算法［4］、蚁群优化（Ant Colony Optimization，ACO）算法［5］、粒子群优化（Particle Swarm Optimization，PSO）算法［6-7］、狼群算法［8］、烟花算法［9］，取得了比较丰富的研究成果。而遗传算法自提出以来，在求解TSP 领域中取得了较好的成果。同传统的PSO算法和ACO算法相比，遗传算法的全局寻优能力强、具有潜在的并行性，可以进行多个个体的同时比较。尽管如此，遗传算法的进化概念不能直接应用于求解汽配件喷涂顺序问题，必须通过将原问题转化为TSP，建立适应的TSP 转化模型，再用遗传算法对模型进行求解从而求解出汽配件喷涂的顺序问题。为此，本文提出了一种基于TSP 转化和遗传算法的优化和求解方法，实验结果表明该优化模型刻画准确、求解算法高效实用。

1 TSP转化与建模

1.1 定义TSP顶点及其距离

在汽配件喷涂生产线上，每一个滑橇上安装的汽配件都要喷涂且只喷涂一次，这非常类似于TSP。设一条生产线共有N个滑橇，将待喷涂的N组汽配件看作是N个TSP 顶点，对它们以一定顺序编号，即构成一个TSP 的顶点集，记为V={v1，v2，…，vN}。

与TSP不同，在汽配件喷涂顺序问题中，任意两组待喷涂的汽配件之间并没有距离的概念。考虑到问题的目标是使喷涂生产线上换色次数尽量少，因此可以用任意两组汽配件的颜色是否发生切换来定义顶点之间的距离。

设N组待喷涂汽配件的颜色共有L种，用自然数1，2，…，L来表示对应的颜色号，顶点vi对应的颜色号记为pi∈{1，2，…，L}，所有顶点颜色号记为P={p1，p2，…，pN}。定义任意两个顶点是否需要换色（颜色是否相同）为其距离，若要换色则距离为1，否则为0，可表示为：

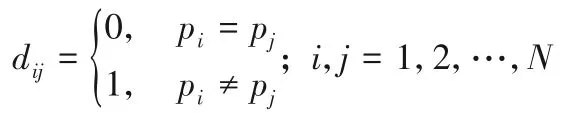
由dij构成的顶点距离矩阵记为D=(dij)N×N，由于dij是0-1变量，因此N个顶点构成的一条TSP路径（一个喷涂序列）的距离之和刚好也能反映喷涂该序列的换色总次数。

1.2 构建TSP模型

与标准TSP 的约束一样，汽配件喷涂顺序问题的N个顶点要构成一条TSP 路径，也要满足任意顶点的出度为1、入度也为1，以及不构成子回路这三种基本约束条件。此外，比起标准的TSP来说汽配件喷涂顺序问题还应当满足喷涂生产的两类限制条件：某些配件的颜色因调色等因素具有互斥性，对应的这些汽配件组将不能安装在相邻的滑橇上喷涂；某些配件的形状容易导致相互之间碰撞和划伤，对应的这些汽配件组将不能安排在相邻的滑橇上喷涂，故将借鉴TSP经典模型，建立适合汽配件喷涂问题的TSP转化数学模型。

类似于顶点距离的定义，可以对任意两个顶点的颜色和类别是否允许相邻进行定义，再用它对TSP 路径的颜色和类别限制进行约束。为便于计算，首先对颜色或类别之间是否允许相邻进行量化定义。设汽配件的类别共有K种，用自然数1，2，…，K来表示对应的类别号，则任意两种颜色或类别是否允许相邻可分别定义为：

由cij，tij构成的颜色和类别的相邻性矩阵分别记为C=(cij)L×L，T=(tij)K×K，矩阵C、T不一定是对称阵，因为有些颜色或类别之间的前后相邻性并不完全相同。

设顶点vi的配件类别号为qi∈{1，2，…，K}，所有顶点的类别号记为Q={q1，q2，…，qN}，则任意两个顶点的颜色和类别是否允许相邻性可分别定义为：

由rij，sij构成的顶点颜色和类别相邻性矩阵分别记为R=(rij)N×N，S=(sij)N×N。

仿照标准TSP的0-1规划模型，设有如下0-1变量：

则可建立汽配件喷涂顺序问题的0-1规划模型如下：

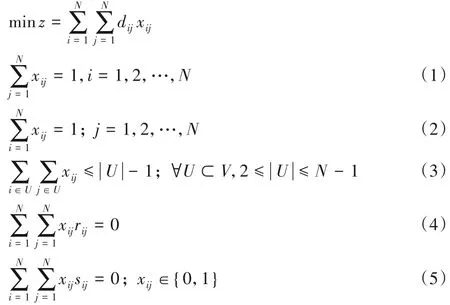
在模型中，约束条件（1）和（2）使得对每一个顶点只能有一条边进和一条边出，约束条件（3）使得不会产生任何的子回路，约束条件（4）和（5）使得在TSP 路径上的相邻两个顶点之间不会出现汽配件的颜色和类别不允许相邻的情形。

2 遗传算法设计

在实际生产中，汽配件喷涂顺序问题的规模较大，现代智能启发式算法［10］是求解这类问题的主要算法，遗传算法［11］就是其中一种高效实用、鲁棒性强的算法，它借鉴生物遗传学原理，模拟自然界生物的遗传进化过程，具有优异的自适应性、并行性和全局寻优能力。遗传算法首先需要为可行解选择恰当的基因编码方案，并产生一定数量的初始种群，然后对种群进行一定次数的遗传进化操作，包括适应度评估、选择、交叉、变异操作，最终获得问题的近似最优解。下面根据汽配件喷涂问题的特点，进行遗传算法的设计。

2.1 编码方案

遗传算法不能直接处理问题空间的参数，需要将其编码成为遗传空间的染色体。遗传算法的鲁棒性强，对基因编码方案要求并不苛刻，但是编码方案对遗传操作有很大的影响，特别是交叉和变异操作。在TSP 的0-1 规划模型中，所有的0-1 型变量xij就是问题空间的参数，共有N2个，如果将这些参数编码成为二进制形式的染色体，当N较大时，会导致染色体的编码长度太长，在计算机存储和遗传操作的运算等方面都会难以处理。除此以外，xij还受到五类约束条件的限制，因此即使生成了编码，也必然存在着大量的无效编码，需要借助额外的算法进行检测和剔除，再重新补充生成合法有效的染色体编码，这必然又增加算法的复杂性。

考虑到汽配件喷涂顺序问题也是TSP 的一类扩展应用，需要求得的最优解就是所有顶点（全部待喷涂的汽配件组）的某个特定的最优顺序，因此可以将这些顶点编号作为问题空间的参数进行编码：一方面满足编码方案的完备性、健全性和非冗余性；另一方面染色体的编码长度从N2位下降到N位，这样遗传算法也容易实现，提高了算法的实用性。一般地，顶点编号以自然数表示，因此在本问题中，采用不重复的自然数对全部顶点进行染色体编码［12］，于是每一个个体的染色体编码可表示为：

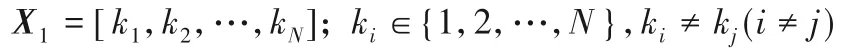
设初始种群规模为m，则可表示为X=[X1；X2；…；Xm]。

2.2 适应度函数

适应度函数用于评估和区分种群个体的优劣，是进行遗传选择的依据。本问题中，由于有生产限制的约束条件，即使采用不重复的自然数编码［13］方案，也仍然无法避免无效编码的出现。此时有两种解决方法：一是设计额外的检测算法，剔除无效编码，再补充生成有效编码；二是将与无效编码对应的约束条件以惩罚分量的形式添加到目标函数中，使得包含有无效编码的个体在遗传进化过程中具有更差的适应度。为降低算法的空间和时间复杂性，提高算法的实用性，本文采用第二种解决方法，并按以下方法构造适应度函数。

由第1 章可知，对任意一个喷涂序列τ={τ1，τ2，…，τN}（τi∈V且互不相同），它的路径长度（换色总次数）、出现配件颜色不允许相邻的总次数、出现配件类别不允许相邻的总次数，可分别用以下公式计算：

其中：f2，f3即是对模型中约束条件（4）和（5）的转化，将其作为惩罚分量，添加到适应度函数中，当其值趋于0 时，喷涂序列中相邻顶点的颜色和类别必定是符合生产要求的。

设三个分量的权重分别为λ1，λ2，λ3∈[0，1]，(λ1+λ2+λ3=1)，则适应度函数为：

可以看到，当适应度函数达到最小时，若分量f2，f3趋于0，则分量f1恰好能近似等于喷涂序列的最少换色次数。

2.3 遗传进化策略

遗传算法的遗传进化策略包括选择、交叉和变异［14］，选择策略可以将种群中适应度高的个体选择出来，交叉和变异策略可以在已选择个体基础上产生新个体，以提高种群的多样性，提高收敛速度。一些研究表明，锦标赛选择策略通用于最大化和最小化问题，在求解精度和收敛速度方面性能优异［15］。本文选择锦标赛选择策略，以此为基础来设计遗传进化策略。

体育运动的锦标赛最早是指单项运动的冠军赛，运动员首先通过分组比赛，才能进入决赛获得冠军。锦标赛选择策略正是借鉴这种赛制规则和赛程安排原理，基本思想是分组和优选，主要操作方法是预先确定一个分组规模，将整个种群随机地分成若干个种群小组，每个小组内只选择组内最优的个体作为遗传的新个体，并将其复制若干份，以保持新个体的规模不变。为提高运算速度，在复制新个体时，可以同步加入个体的交叉和变异策略。由于编码方案是不重复的自然数编码，个体之间进行基因交叉，很容易导致两个个体的基因都出现重复的数字，变成非法编码，因此本文不采用交叉策略，着重设计了三种变异策略，分别用于不同的新个体，以提高新个体的多样性。

第一种变异策略是两点基因交换（Swap），即随机产生两个基因点，将个体中这两个基因点的值进行交换。第二种变异策略是基因片段翻转（Flip），即随机产生两个基因点，将介于这两个基因点内的基因片段进行翻转。第三种变异策略是基因片段滑动（Slide），即循环移位，具体做法是随机产生两个基因点，将介于这两个基因点之内的基因片段作循环移位一次，可以向左移位，也可以向右移位。根据上述遗传进化策略去具体求解汽配件最优喷涂顺序的操作示例如图2所示。

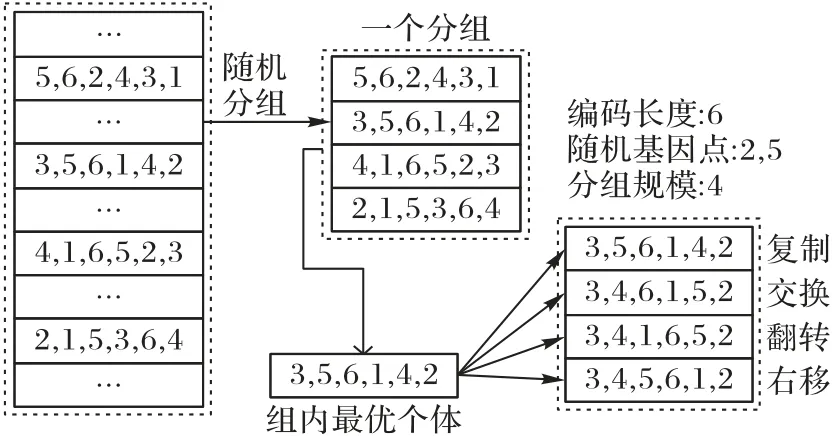
图2 遗传进化策略的操作示例Fig.2 Operation example of genetic evolution strategy

2.4 算法流程

根据遗传算法的基本流程，结合上述算法设计，汽配件颜色喷涂顺序问题的遗传算法求解流程如图3所示。

其中，汽配件初始数据主要包括：待喷涂汽配件的类别K、颜色L、组数M，配件之间颜色不允许相邻的情况C、类别不允许相邻的情况T，以及由上述数据计算得到待喷涂序列的顶点集V、颜色号P、类别号Q、任意两个顶点的换色距离矩阵D、颜色相邻性矩阵R和类别相邻性矩阵S。

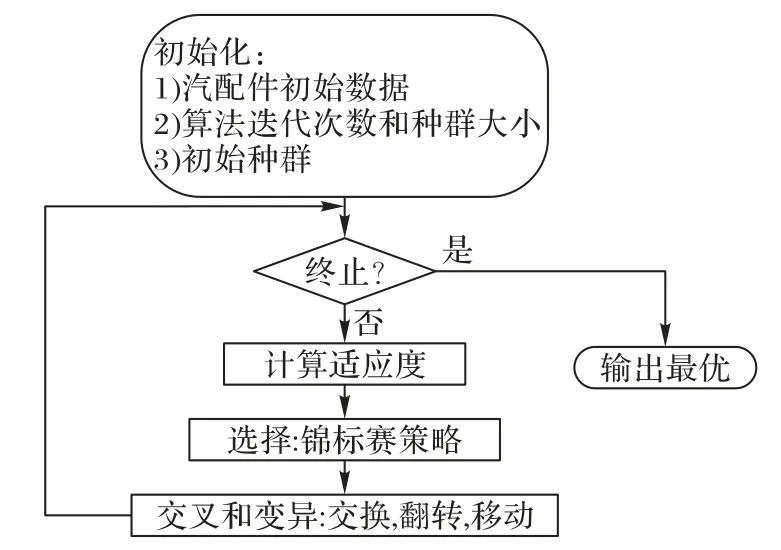
图3 遗传算法的流程Fig.3 Flowchart of genetic algorithm

3 仿真实验与结果分析

3.1 实验数据准备

为检验算法的有效性和实用性，参考一些企业的实验生产数据，本文将待喷涂的汽配件个数最大设置为293 个，作为一条生产线的一个工作日的生产任务，这些汽配件包括31 个类别，需要喷涂的颜色有10 种，不同类别的汽配件、不同颜色的汽配件分为83组，全部初始实验数据如表1。

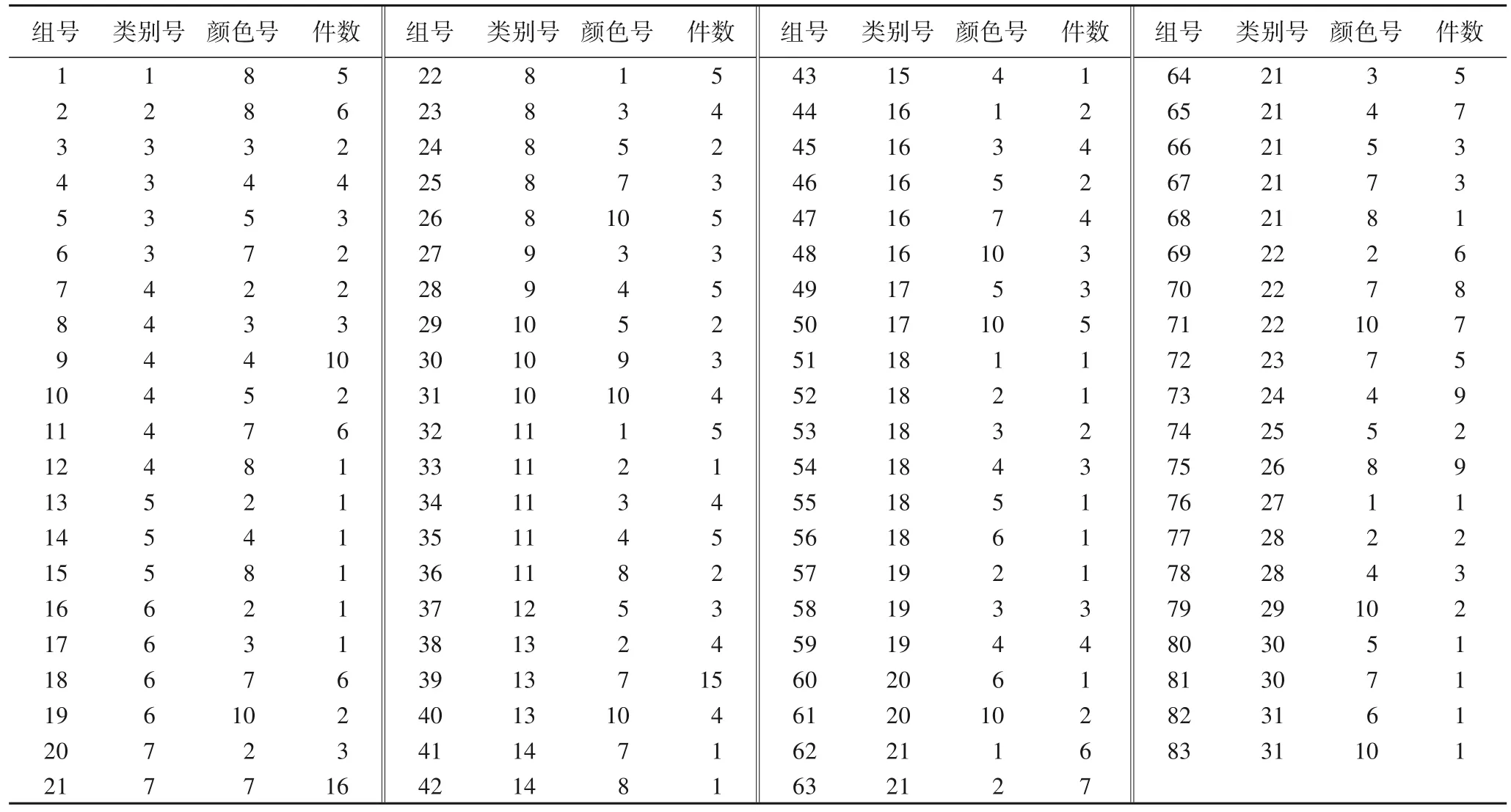
表1 待喷涂汽配件的初始数据Tab.1 Initial data of auto parts to be sprayed

汽配件的颜色约束为：颜色号｛1，2，3，6｝中的任意颜色之后不能接4 或10 号颜色；4 号颜色后面不能接7 或9 号颜色；10 号颜色前面只能是4 号颜色。汽配件的类别约束为：22 号配件不能与｛11，21，23，24，26-31｝中任意一种配件相邻；23号配件不能与｛11，21，22，24，26-31｝中任意一种配件相邻。

为更好地检验上述TSP 模型及对应遗传算法对不同规模数据的求解性能，现将上述初始数据进一步分组为较小规模、中等规模和较大规模的三组数据，具体数据如表2。

表2 三种规模的实验数据Tab.2 Experimental data of three scales

对上述三种规模数据，汽配件个数分别为64、93、293，对应于TSP，即是分别有64、93、293个路径顶点。由于本文讨论的汽配件颜色喷涂问题的目标是使换色次数尽量少，而上述三种规模数据中汽配件的颜色数分别为5、7、10，因此它们的理论最优解分别为5、7、10。

3.2 结果分析

本次实验硬件环境为AMD A8-45000M CPU/8GB/Win 7系统，编程环境为Matlab R 2018a。对表2 的三种规模数据，按流程图3编程，在不同算法参数下求解结果如表3。

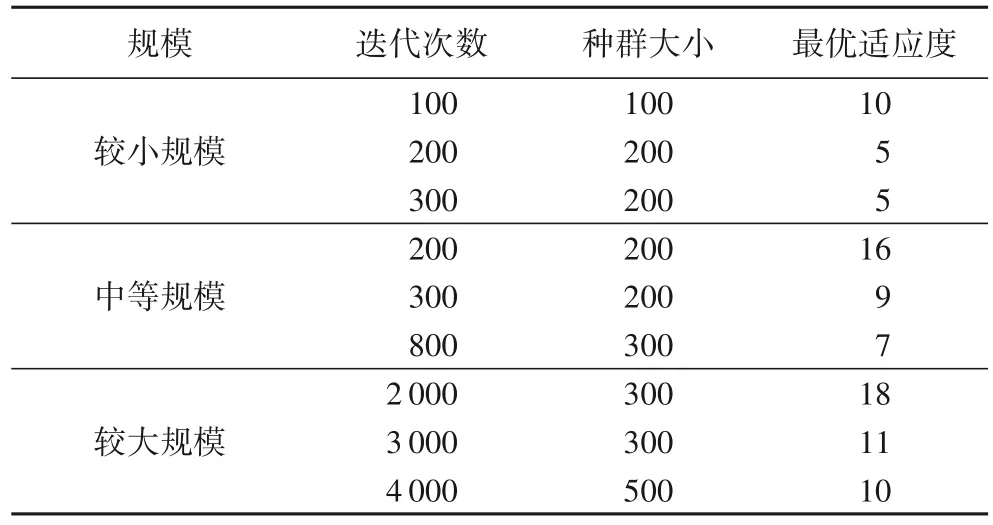
表3 三种规模数据在不同算法参数下的求解结果Tab.3 Results of solving data with three scales under different algorithm parameters

从表3 中对中等规模和较小规模的求解结果中可以看出，在迭代次数和种群规模适中的情况下最优适应度f分别为7 和5，其中3 个分量都值为f1=10，f2=0，f3=0，即这两种规模汽配件数的最优喷涂序列换色次数都为颜色总数，违背颜色约束的次数都为0，违背配件类别约束的次数都为0。

同样的，在迭代次数和种群规模适中的情况下，对较大规模的汽配件初始数据用本文设计的模型和算法进行计算时求解结果得到的最优适应度为f=10，其中3 个分量值为f1=10，f2=0，f3=0，即上述最优喷涂序列的最少换色次数为10次，违背颜色约束的次数为0，违背配件类别约束的次数为0。

从以上结果可以看出，不管数据规模的大小通过本算法的求解都可以得到最优解，充分证明本文的基于TSP 转化和遗传算法求解汽配件最优喷涂顺序的优化方法是有效的。随着迭代次数和种群规模的增加，还可以进一步提高算法优化能力，限于篇幅这里不再一一列举。

图4 是不同规模实验数据下选择第三行数据所做的适应度值随运行次数的变化曲线。从图4 中可以看出随着迭代次数的增加，适应度的值逐渐接近于理论最优解。

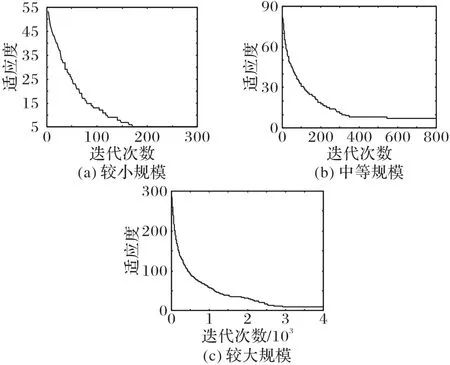
图4 不同规模数据的适应度进化曲线Fig.4 Fitness evolution curve of data with different scales

3.3 算法求解性能分析

表4是3.2节中不同规模数据求解结果的效率对比，其中当较小规模数据设置为表3 的第3 行参数时取得最优解5 的百分比为60%；参数为中等规模第3 行数据时，取得最优解7的百分比为76%；当参数设置为较大规模第3 行数据时取得理论最优解10的百分比为42%。

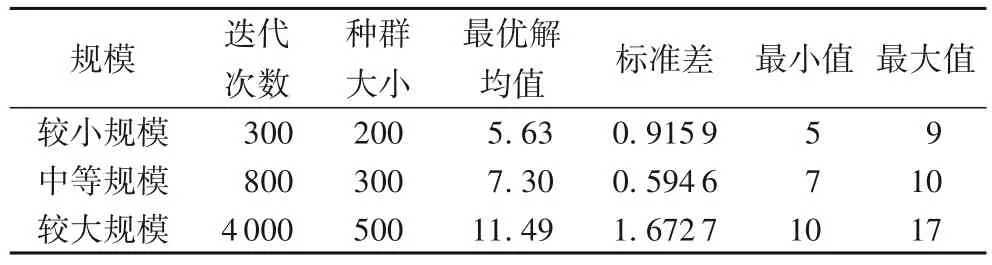
表4 本文算法对三种规模数据在100次运行下的求解性能Tab.4 Solution performance of the proposed algorithm on data with three scales under 100 runs

从表4 中可以看出，在迭代次数和种群规模适中的情况下，不管大小规模的初始数据在本文设计的优化方法的计算下都可以多次得到理论最优解，并且得到最优解的规模的平均值都已经非常接近最优解，标准差也非常小，表明本文设计的遗传算法，在种群规模适中的情形下，可以得到非常优质的遗传进化效果。

图5 是对应于图4 的100 次运行的适应度波动曲线，由此图5 可以看出适应度一直在最优适应度附近波动，表明本算法有较高的概率可以求得精确最优解或非常接近最优解的值。所以，本文所建立的数学模型及设计的遗传算法是稳定和实用的，对汽配件喷涂顺序问题的优化效果显著。

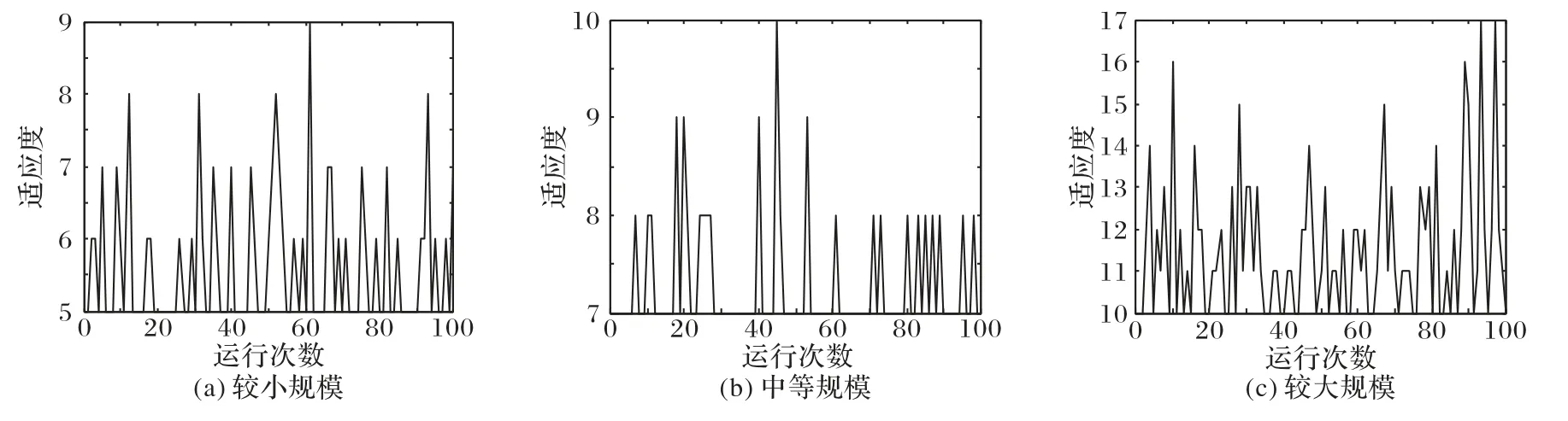
图5 100次运行适应度波动曲线Fig.5 Fitness fluctuation curve of 100 runs

本文的数学模型及遗传算法对更大规模的汽配件喷涂顺序问题仍然是有效和实用的，限于篇幅，这里不再论述。

4 结语

本文借鉴TSP 的建模和求解思路，建立了汽配件喷涂顺序问题的数学模型，设计了针对性和实用性强的遗传算法来求解，通过实验数据的验证，求解结果完全能满足实际的生产要求，对企业减少生产成本、提高生产效率具有很好的指导意义。

本文的数学模型及遗传算法仍然适用于数据规模更大的汽配件喷涂问题，还可以推广应用于其他企业生产作业调度［16］等问题。但是由于实际生产实践中汽配件喷涂问题的复杂性，本文的方法还有不足之处，有待今后继续进行研究完善。如果综合考虑到大规模汽配件喷涂时放置汽配件的支架数目对汽配件喷涂顺序的影响，如果动态调度配件种类颜色以及汽配件数目，建立的模型将更加有实际意义。