大型压力输水管道泄漏监测方法的试验研究
林天翔,冯少孔,叶冠林,朱新民,车爱兰
(1.上海交通大学 船舶海洋与建筑工程学院,上海 200240; 2.中国水利水电科学研究院,北京 100038;3.流域水循环模拟与调控国家重点试验室,北京 100038)
在现代化的进程中,石油、水等液体资源的输送问题一直广为人们关注,尤其是水资源,与日俱增的城市用水需求促进了大型压力输水管道的发展,但由于大型埋地管道水压大、管道材料性能劣化等原因导致近年来以爆管为代表的压力流体管道安全事故频发,仅2015年被媒体报道的爆管事故就高达178起[1],这给国家造成了巨大的经济损失和社会影响。
爆管的形式有两种:突发式爆管和渐进式爆管,前者由水锤作用[2]和管路堵塞等引起;后者为管道局部泄漏引起,进一步发展将导致危害性集中泄漏[3]。对于突发式爆管,可以通过已有技术手段加以规范管理进行有效规避,但渐进式爆管成因复杂,难以避免,其爆管过程一般分为三个阶段:平稳阶段、渐变阶段、突变阶段。平稳阶段压力正常,无或仅有轻微泄漏,管道结构强度和稳定性未破坏。对于大型埋地输水管道,维修工作所需费用较大,在平稳阶段暂可不作处理。渐变阶段处于过渡期,泄漏量增大,是爆管防治的关键阶段。若渐变阶段不及时预警,并进行维护,随着损坏的进一步发展至突变阶段,泄漏量将无法控制,导致管道发生爆裂解体。
目前防控爆管发生一般采用停水检测的方式,定期检查维护,这种方式存在一些局限性,监测时间不连续,往往在泄漏中后期发生二次破坏时才被发现,无法及时提供爆管预警。即使在最佳情况下,检测员也不能可靠地确定泄漏孔的大小,不便采取进一步维修措施,所以一种连续高效的爆管预警及监测方法亟待研究,从而保障城市的用水安全。
国内外学者提出可以利用泄漏噪声信号对管道爆管提供监测分析和预警指导。Anastasopoulos等[4]证明通过分析声信号来实现管道泄漏的在线监测是一种十分有效的手段。Ahadi等[5]将塑料管道泄漏信号进行短时傅里叶变换和小波变换,对泄漏信号的时域特征方面进行了分析;Ozevin等[6]利用互相关函数确定泄漏信号到达时间差,引入几何连通性,从而有效地确定了管道泄漏的多维空间位置;Sato等[7]用模式识别技术辅助声学方法,提出了一种对采集地下泄漏管道的声音和伪声音样本进行主成分分析的泄漏监测方法;Zhang等[8]为及时发现输水管道的泄漏情况,提出了一种完整的泄漏声信号相关器检漏方案;刘敬喜等[9]从波传播衰减特性方面对弹性介质中充液钢质管道和PVC管道进行了研究。这些研究在一定程度上都肯定了泄漏信号对管道故障检测具有重要意义,通过信号特征分析可以判断泄漏的发生,但对管道泄漏发生时管道破坏程度无法进行评判。当泄漏量很小时,可能导致误判;泄漏量过大时,检修时间和措施应有严格标准,这样泄漏事故危险性才能得到有效降低。
目前常用的管道泄漏噪声的监测方法有听音监测法[10]和声波监测方法[11]等,它们利用传感器在路面或管道外壁收集特征信号,再通过信号分析判断管道泄漏的发生。但是,这些方法受环境噪声影响大,只适用于埋设较浅的管道,有很大的局限性。对于大型压力输水管道而言,埋设地点一般选在输水任务紧迫、需求量大的地区,沿线经济发达,若开挖埋设连续监测设备,造成的社会影响和资金投入巨大,不具备可行性,且其埋深一般超过10 m,噪声信号传至地面时基本已完全衰减。为实现长期连续监测压力管道的目标,本研究将水声检波器安装在管道内对噪声信号进行长期监测,此种方法既适用于新建压力输水管道,亦适用于已建成的压力输水管道,无需再次开挖埋设,满足了输水管道工程停水检修期较短的要求,便于监测系统的维修和升级改造。与此同时,水声检波器被安放在管道内壁,泄漏噪声的高频成分在水体衰减较快,而低频成分以振动信号的形式沿输水管壁传播,信号更接近泄漏源本身,受管道材料、土壤类型和环境影响较小[12-13],故本研究认为水声检波器接收的大部分信号属于振动信号。
本研究通过控制阀门开闭、孔径大小和输水管压力变化来模拟实际运行管道的不同泄漏状态。首先用安放在管道内壁的水声检波器采集泄漏状态和非泄漏状态下两种原始振动信号,再经过滤波处理得到分析信号。通过比较分析信号的相关特性研究输水管道泄漏信号发射机理,并研究管道破坏参量(管道运行压力和泄漏孔面积)与泄漏振动信号特性之间的关系。
1 压力管道泄漏监测原理
噪声声源一般可分为单极子源、偶极子源和四极子源三个阶次。任何实际声源都可看作是由一个分布系统下多个适当相位和幅值的单极子所组成的。对于振动声学问题,前人研究较少,且往往仅通过数值模拟进行计算分析。不过Howe[14]的研究表示:所有声源的发生原理都可以归结于气动声学问题。毛义军等[15-16]也对气动声学和振动声学进行了相关性分析,证明了声类比理论不仅能在气动噪声的监测方面有很好的应用,还适用于振动噪声的监测,是一种普适的理论。同时,赵威等[17]采用变分形式的Lighthill声类比方程来分析在管道内传播的噪声问题,也充分证明了声类比方程在振动噪声问题上的应用。这些研究为本研究提供了一个很好的解决思路,即参照声类比理论来探究对振动噪声的监测原理。
声类比理论[18-19]在气动噪声问题上应用十分广泛,它是Lighthill在20世纪50年代最先提出来的,其证明了在自由释放状态下泄漏声功率与速度的八次方成正比,噪声呈现四极子声源特征,如式(1)
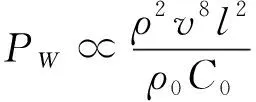
(1)
式中:v为流体泄漏速度;ρ为泄漏孔处流体密度;ρ0为流体初始密度;C0为当地的声速;l为泄漏孔尺寸。
之后Curle[20]在Lighthill理论基础上继续研究,考虑了静止固体边界的影响,发现噪声呈现偶极子声源特征,且提出偶极子声源的泄漏声功率与速度的六次方成正比,但并未涉及运动固体边界和流体的互相作用。而Ffowcs Williams和Hawkings应用广义函数法将Curle的结果扩展到考虑运动固体边界对信号的影响,得到著名FW-H方程[21]。
研究表明:管道泄漏声由四极子声源和偶极子声源两种声源叠加产生[22],故泄漏声功率与流体速度的次方关系应介于6~8。同时,压力管道的泄漏问题属于流固耦合问题。一方面,流体与管道间的作用十分复杂,在泄漏过程中,随着泄漏程度的增加,管道压力下降,其边界效应会有所减弱;另一方面,噪声在水环境下的传播发生衰减,泄漏声功率变小。考虑到上述情况,本研究建立理论模型时设泄漏声功率与速度的n次方(6≤n≤8)成正比,引入比例系数K,即:

(2)
假设流体密度、当地声速等为定值,对式(2)进一步简化得
PW=ηvnl2=λvnS
(3)
式中:η、λ均为常量比例系数;S为泄漏孔面积。
由伯努利方程知

(4)
式中:ΔP为管道泄漏前后压力差;v0为管道内液位下降的速度;v为水射流速度;h为液位高度。
由于本研究研究对象是大型压力输水管道,渐变阶段的泄漏孔径一般小于20 mm,相对于输水管径而言极小,属于小孔泄漏问题[23]。故管道内液位下降速度v0很小,可忽略不计。
即射流速度可表示为

(5)
将式(5)代入式(3),得:
(6)
又因为泄漏声功率与振幅A的平方成正比的关系,引入系数μ即
PW=μA2
(7)
联立式(6)、(7)两式得
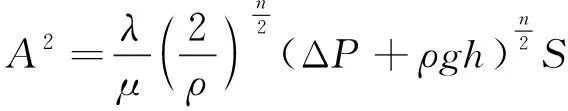
(8)
管道泄漏时,泄漏孔处内外压差是动态的,难以直观有效地对压差进行评判,并且对于大型压力输水管道而言,小孔泄漏模型引起的压力变化较小,鉴此,本研究直接利用水管运行压力F作为评价指标,认为水管运行压力F的值近似等于(ΔP+ρgh)的值。
令F=ΔP+ρgh
(9)
则式(8)可变为
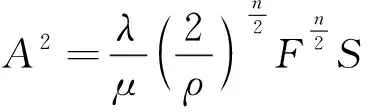
(10)
式中:λ、μ、n均为比例常量;ρ为定值。
从式(10)知振幅A与泄漏孔面积S和水管运行压力F之间是幂函数关系。若水管运行压力F一定,则振幅A的平方与泄漏孔面积S成正比;若泄漏孔面积S一定,则振幅A的平方与管道运行压力F的n/2次方成正比。
对式(10)两边取对数,并归纳后得
(11)
式中:A为应变量,F、S为自变量;n为待求常数。
由式(11)可看出:信号振幅的平方与压力和泄漏孔面积幂之积在分别取对数后呈现线性关系。为更加方便求解,令:
(12)
改写式(11)得
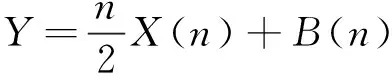
(13)
2 试验概要
为进一步验证利用泄漏信号数据分析大型压力输水管道泄漏程度的方法,探究第一节推导公式中未知的待求系数的取值范围,本研究共设计了14个工况的试验来模拟运行管道发生泄漏时的特征。
试验装置的主体结构是一个长12 m,外径1 m,管厚0.02 m的大直径钢管,沿管道底部中心轴线分别在内壁安装一组阀门,并采用水声检波器作为泄漏噪声传感器。同时,水声检波器通过管卡也安装在管道两端部的内壁上,以便更加满足实际工程中监测工作的要求,装置如图1所示。

图1 试验装置图Fig.1 Diagram of test equipment
水声检波器是圆柱形,以减少涡流振动。外管由聚氨酯材料制成,长25 cm,外径4 cm,管厚2 mm。在外管中部内置一个压电陶瓷式水声换能器,并用凝胶填充。凝胶材料比水的密度略小,这使检波器整体密度与水的密度基本相同,以保证水声检波器在水中处于平衡状态,尽量减少其对试验数据的干扰,如图2所示。

图2 水声检波器示意图Fig.2 Diagram of the hydrophone
阀门孔直径为2 mm、4 mm、8 mm、14 mm,试验时将试验管道置于大型高压试验台上,通过打开阀门来模拟压力管道破损引起的泄漏状况。在每种泄漏状态下对钢管中的水分别加压,从而得到不同压力、不同泄漏孔径下的信号。由于泄漏量较少时,泄漏信号特征不明显,故本试验在2 mm阀门孔径下仅进行0.6 MPa和0.8 MPa两种工况,其余每个孔径都完成0.2 MPa、0.4 MPa、0.6 MPa、0.8 MPa四种压力工况。具体过程为:在每个工况下,首先向管内充水加压到设计压力,然后稳压并测量10 min,然后打开阀门模拟泄漏并采集数据10 min,最后泄压,此为完成一个工况的试验。
本试验中数据采样间隔为0.125 ms,数据个数为65 536,采集时间为8.192 s,连续记录。试验所用仪器具体技术参数如表1所示。
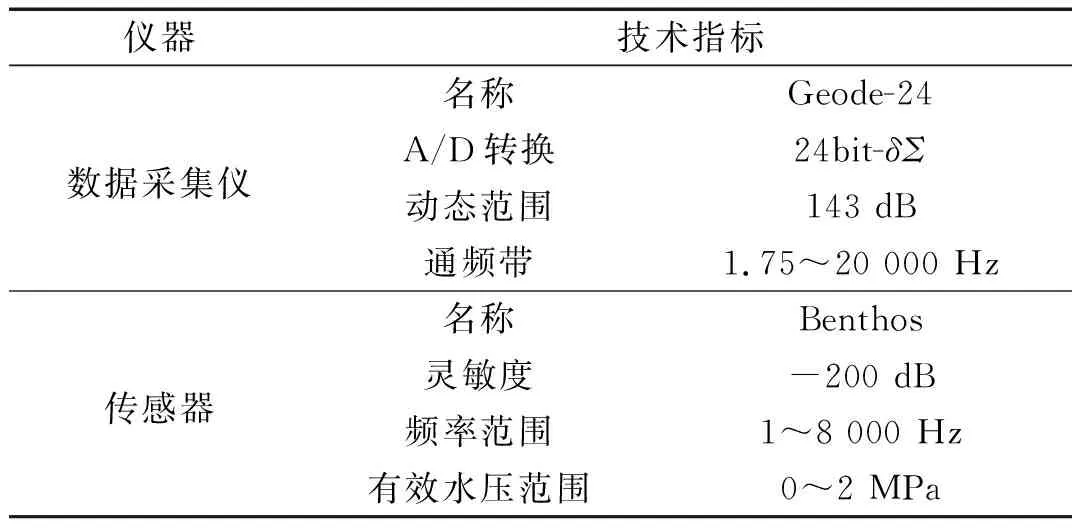
表1 试验仪器技术参数
3 试验结果分析
图3为0.4 MPa压力工况下所得的振动信号输出波,1号、2号检波器是阀门闭合时即非泄漏状态下所记录的波形,1#号、2#号是在8 mm泄漏阀开启后即泄漏状态下检波器记录的波形。从图3可看出,1号和2号、1#号和2#号的信号特性基本一致,这说明振动信号沿管道左右两个方向传播过程中水压力波动的影响很小,但不管是1号和1#号还是2号和2#号振动信号振幅变化极大,两者相差约10倍,这有效地证明了压力管道泄漏所引起的信号有足够的强度能从背景噪音中被监测出来。其余工况下同样可证明该结论,不再赘述。
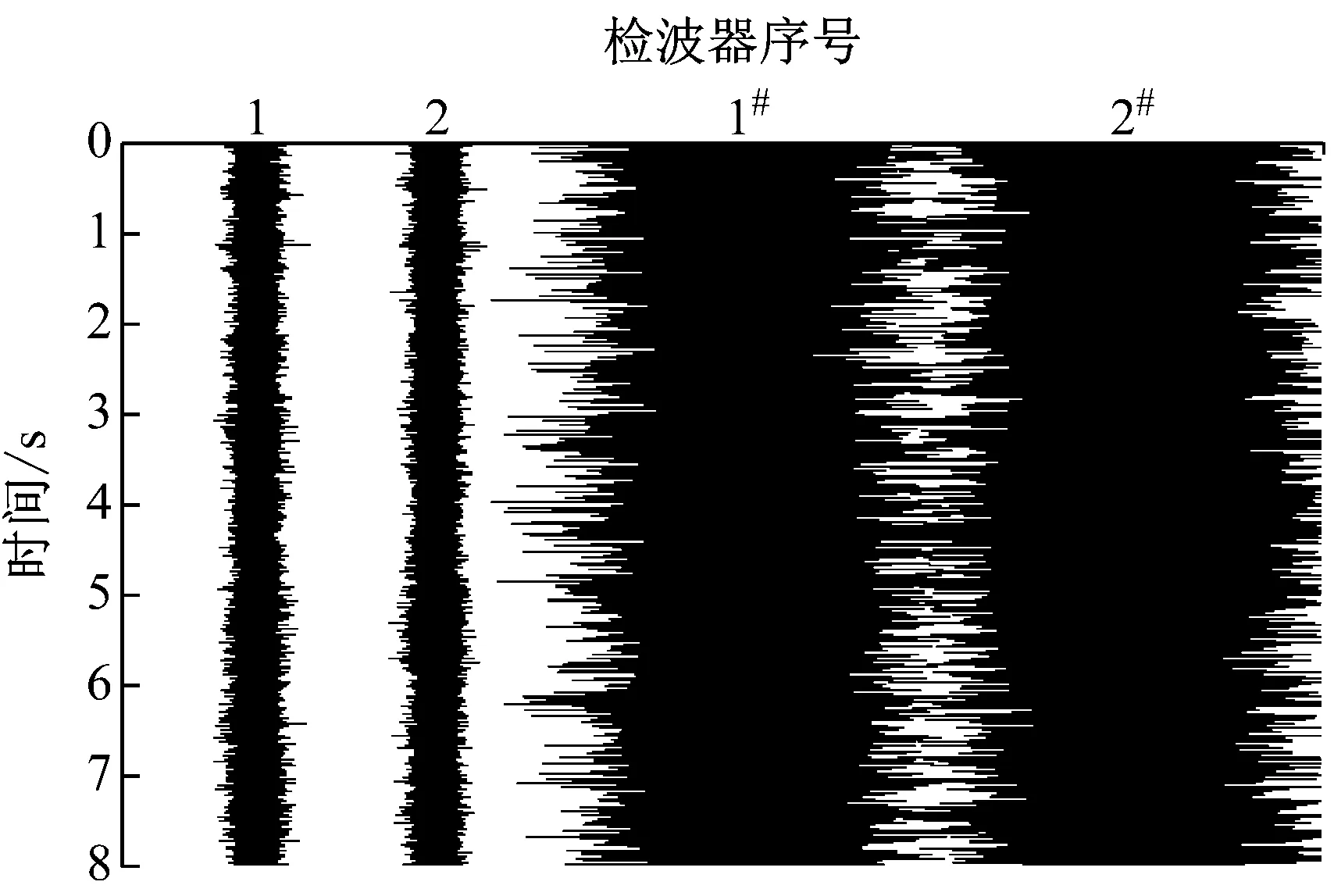
图3 0.4 MPa压力下8 mm泄漏阀开启前后加速度时程Fig.3 Acceleration time histories before and after opening of8 mm valve at 0.4 MPa pressure
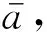
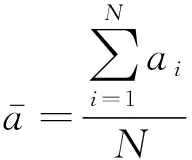
(14)
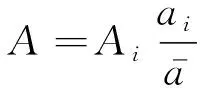
(15)
当管道发生泄漏时,水管运行压力、泄漏孔面积都会不同程度地影响着泄漏信号的传播和特征规律。研究通过将泄漏孔面积和水管运行压力作为单一变量,分别考虑在各组水管运行压力下振幅随泄漏孔孔面积的变化规律和各组孔径下振幅随运行压力的变化规律,来验证表达式(10)反映出的振幅A与泄漏孔面积S和水管运行压力F之间的幂函数关系。
图4和图5是基于幂函数模型[Y=aXb]绘制出的数据拟合图像,表2和表3为所拟合得到的最优幂函数表达式和可决系数。当压力改变时,泄漏孔处湍流流场对空气产生扰动,流速发生改变,流体与管壁的摩擦加剧,由图4和表2可看出,在不同的孔径下,函数次数均大于1,泄漏信号振幅随着水管运行压力增加而增加,且孔径越大,泄漏信号振幅-运行压力曲线越陡。表2中拟合出的函数次数基本符合n的取值范围。由图5和表3可看出,拟合函数次数在1/2左右,在各组水管运行压力下,随着泄漏孔面积的增加,泄漏信号振幅也不断增加,但增加幅度减小,有变平稳的趋势。

图4 管道运行压力对泄漏信号振幅影响Fig.4 Influence of pipeline pressure on leakagesignal amplitude

图5 泄漏孔面积对泄漏信号振幅影响Fig.5 Influence of the area of leakage hole onleakage signal amplitude

表2 不同孔径下管道运行压力与泄漏信号振幅的拟合方程
这些规律与工程实际十分相符,在泄漏孔径一定时随着运行压力增大,水的流速加快,泄漏信号必然会增大,没有发生爆管之前信号强度不会发生较大衰减,但当泄漏孔面积不断增大时,水管运行压力也会受到泄漏面积的影响,故泄漏信号不可能无限增大,当泄漏破坏到一定程度后,泄漏信号将会趋于稳定,甚至略有降低。这给了检测人员一个极为重要的提醒,在运行压力较大时,一旦发现有泄漏迹象,数据的读取一定要更加及时,否则估量的泄漏程度可能会偏小,给事故造成更大的损失。

表3 不同运行压力下泄漏孔面积与泄漏信号振幅的拟合方程
结合第一章压力管道泄漏机理分析,信号振幅的平方和泄漏孔面积幂乘与压力的乘积在分别取对数后呈线性关系,且n在6~8。本研究通过取n=6、6.5、7、7.5、8,并结合试验数据求得(X,Y),从而来探究式(12)和式(13)。
将(X,Y)数据点表示在图6中,并标注出趋势线的方程和可决系数。由图可知,Y和X之间都表现出明显的线性相关关系,数据点拟合的趋势线斜率大致相同,通过趋势线斜率反算得到的n值在6.2~6.5,这与设定的n值相差较大。本研究是小孔泄漏问题,很小的泄漏孔面积计算得到的X值自然也较小,这就导致了数据点变化幅度较小、趋势线斜率稳定的结果,但数据的离散性随着设定n值的增大而增大。对于B(n)而言,它的范围在4.28~5.34,随着n的增加,B(n)有减小的趋势。
为验证理论公式的正确性,可进一步探究B(n)与n之间的关系。将式(12)中B(n)进行对数的基本变换,可得到一个明显的线性表达式
(16)
同时,用图6中拟合得到的B值与n值绘成图像,如图7所示,图像符合线性表达式(16)特征。
拟合直线表达式为
B(n)=8.539 8-0.532 7n
(17)
利用B(n)代入式(11)~式(13)可得n的经验值,具体计算过程由式(18)和式(19)示出,求得n≈6.4。
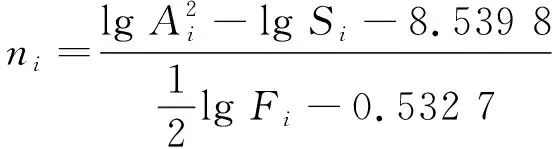
(18)
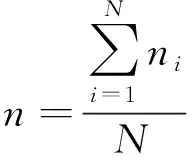
(19)
故水管运行压力、泄漏孔面积与泄漏振幅之间的经验公式为

(20)
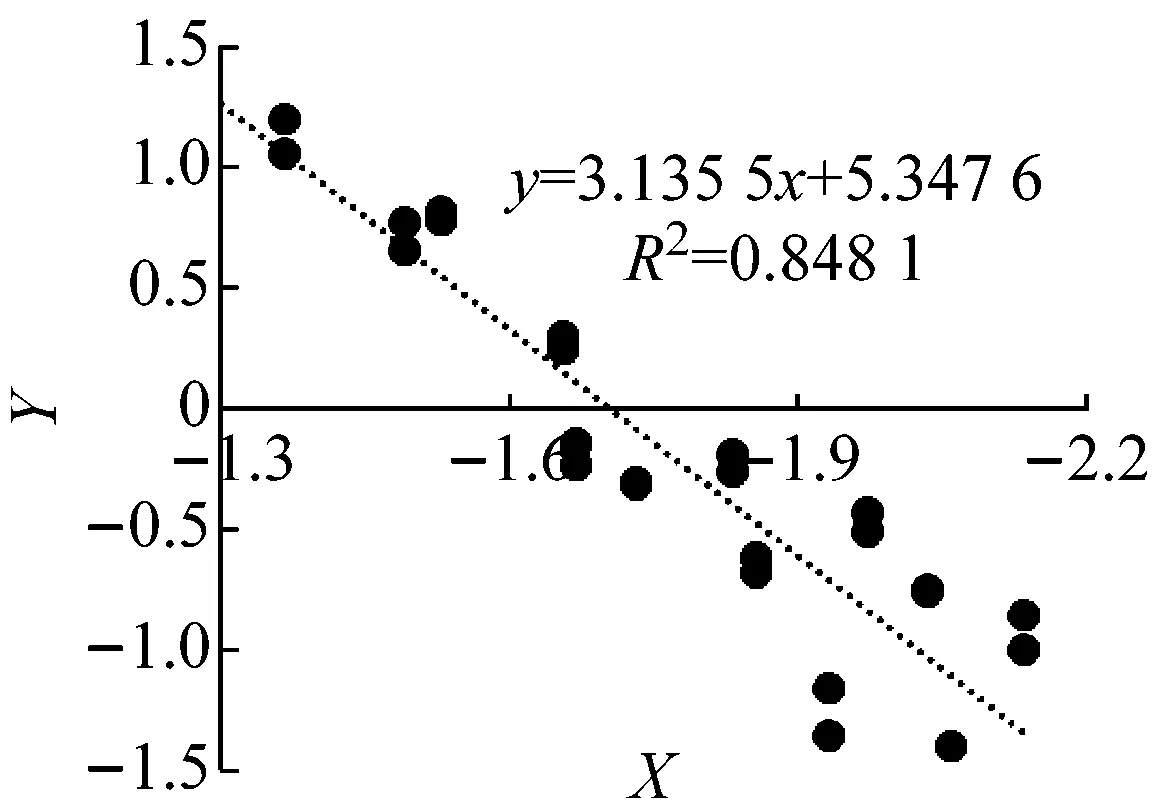
(a) n=6(b) n=6.5(c) n=7

(d) n=7.5(e) n=8图6 依据式(12)计算获得的X与Y关系曲线Fig.6 X-Y curves obtained by formula (12)
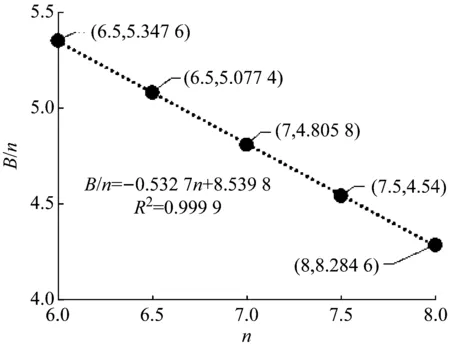
图7 B(n)与n的关系曲线Fig.7 Matching curve between B(n) and n
4 结 论
本文参照声类比理论模型探究了泄漏噪声的监测原理,并通过控制管道压力和阀门孔径开展了14组大型压力输水管道的泄漏模拟试验,分析试验数据可得出以下几点结论:
(1) 本试验中,压力输水管道泄漏引起的信号有足够的强度从背景噪音中被监测出来,泄漏前后信号振幅变化明显。由水声检波器接收到的泄漏信号大部分为低频成分,以振动信号的形式沿管壁传播,其声源以偶极子声源为主。
(2) 在各组泄漏孔径下,泄漏信号振幅随着水管运行压力增加而增加,且增幅较大。在各组水管运行压力下,随着泄漏孔面积的增加,泄漏信号振幅的平方与泄漏孔面积成正比,先增长较快,变化过程中在增幅减小,最终趋于平稳。
(3) 理论分析表明,信号振幅的平方与压力和泄漏孔面积幂之积在分别取对数后呈线性关系。实际工程中水管运行压力已知,监测时可预先判读波形幅值,通过本研究得出的泄漏信号振幅与水管运行压力、泄漏孔径之间的经验关系定量估算泄漏孔大小,从而推测泄漏程度。根据泄漏程度采取相应应对措施,有效地防止爆管的发生。

