基于模糊神经网络逆系统的五自由度无轴承永磁同步电机自抗扰控制

朱熀秋，顾志伟

(江苏大学 电气信息工程学院，江苏 镇江 212013)

0 引 言

无轴承永磁同步电机(bearingless permanent magnet synchronous motor, BPMSM)是集磁轴承技术与永磁同步电机技术于一体的新型电机，不仅具有磁轴承无机械摩擦、无需润滑、噪声小、使用寿命长等优良特性，还具有永磁同步电机功率密度大、效率高的优点，在航空航天、生命科学、半导体制造等领域具有广阔的应用前景[1-4]。

目前研究较普遍的是二自由度无轴承永磁同步电机(2-degree-of-freedom bearingless permanent magnet synchronous motor, 2-DOF BPMSM)，电机转子的一端用调心球轴承固定，转子只能实现径向两个自由度悬浮，不能轴向移动，没有真正意义上实现电机的无轴承化，而五自由度无轴承永磁同步电机(5-degree-of-freedom bearingless permanent magnet synchronous motor,5-DOF BPMSM)用三自由度混合磁轴承(3-degree-of-freedom hybrid magnetic bearings,3-DOF HMB)代替调心球轴承，实现了转子另外两个径向自由度和一个轴向自由度的悬浮控制，真正意义上做到了电机的无轴承化。因此，对其展开深入研究具有重要意义。

5-DOF BPMSM是一个多变量、非线性、强耦合系统，其悬浮力与电磁转矩之间以及各悬浮力之间都存在着较强的耦合。因此，实现5-DOF BPMSM悬浮力与电磁转矩之间以及各悬浮力之间的解耦控制是其能稳定运行的前提。逆系统方法是对非线性系统进行解耦控制常采用的方法，该方法需要被控对象的精确数学模型[5]，而由于5-DOF BPMSM的复杂性，其精确数学模型通常很难获得。针对一些非线性系统难以通过精确数学模型获得逆系统的问题，文献[6]提出使用神经网络来构建被控对象的逆系统，但是神经网络存在“黑箱”性，并且易陷入局部极值。文献[7]提出使用支持向量机来构建被控对象的逆系统，但是支持向量机的学习能力和泛化能力很大程度取决于参数的选择，并且存在参数寻优问题。Takagi-Sugeno(T-S)型模糊神经网络由神经网络与T-S型模糊推理系统相结合而成，同时具有神经网络出色的非线性逼近能力以及T-S型模糊推理系统出色的模糊信息处理能力，近年来已被广泛应用于非线性系统的辨识[8-9]。因此，可以使用T-S型模糊神经网络来构建5-DOF BPMSM的逆系统，但是在实际应用过程中，使用T-S型模糊神经网络构建的逆系统不可避免地存在建模误差，所以不能仅将构建的逆系统作为5-DOF BPMSM的唯一控制器，必须设计相应的附加闭环控制器才可以保证5-DOF BPMSM的稳定性。文献[10]设计了专家PID控制器来保证系统的稳定性，但是该控制器过度依赖专家知识和操作人员的经验，无法避免人为因素造成的误差。文献[11]设计了内模控制器来增强系统的鲁棒性，但是理想的内模控制器在实际生产条件下无法实现。目前，韩京清研究员提出的自抗扰控制理论已在众多领域得到成功应用，依照该理论设计的自抗扰控制器不依赖被控系统的数学模型，可将系统受到的内外部扰动看成总扰动加以观测并进行补偿，能有效增强系统的抗干扰能力，保证系统的稳定性[12]。文献[13]设计了自抗扰控制器对四旋翼飞行器进行控制，使系统很好地适应了自身载荷和外部环境变化的影响，满足系统姿态调节快、稳定性高的控制要求。文献[14]在传统的自抗扰控制器中引入蚁群优化算法，优化了自抗扰控制器参数，使系统获得更强的鲁棒性。

本文针对5-DOF BPMSM这一多变量、非线性、强耦合的系统，将使用T-S型模糊神经网络构建逆系统的方法与自抗扰控制理论相结合，提出了一种基于T-S型模糊神经网络逆系统的自抗扰控制方法来实现其解耦控制，并通过仿真和实验验证了所提控制方法的可行性与有效性。

1.1 5-DOF BPMSM结构及运行原理

5-DOF BPMSM由3-DOF HMB以及2-DOF BPMSM组成，其结构如图1所示，其中，3-DOF HMB实现转子径向两个自由度以及轴向一个自由度的悬浮控制，2-DOF BPMSM实现转子径向另外两个自由度的悬浮控制以及电机的转速控制。

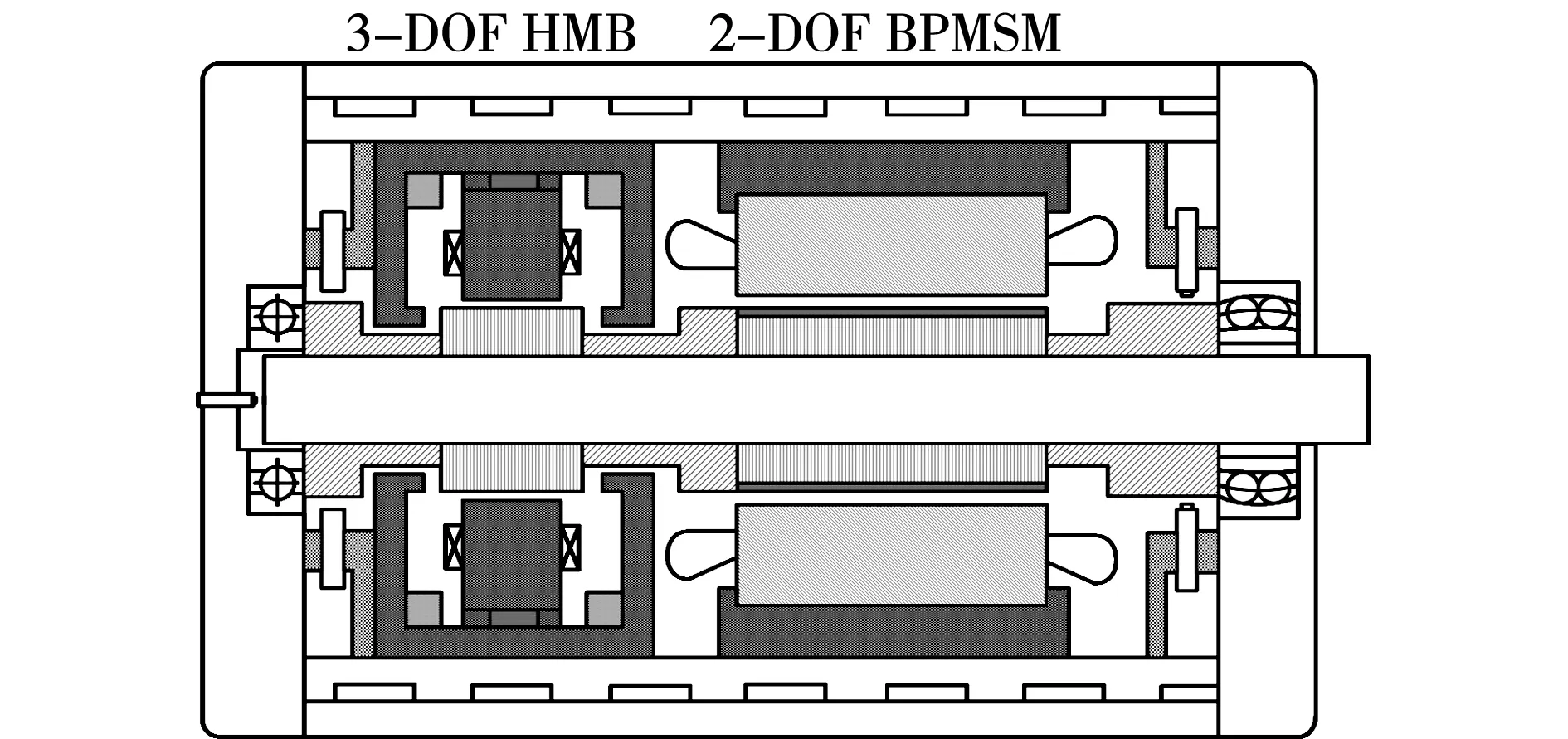
图1 5-DOF BPMSM结构示意图Fig.1 Structure chart of the 5-DOF BPMSM

1.2 5-DOF BPMSM数学模型

图2是5-DOF BPMSM转子结构示意图，3-DOF HMB在位置A处，2-DOF BPMSM在位置B处。用下标“a”表示3-DOF HMB有关的变量，用下标“b”表示2-DOF BPMSM有关的变量。图中：x、y和z分别代表转子的三个坐标轴；坐标原点O与转子质心平衡位置重合；Fax、Fay和Faz分别为3-DOF HMB在x、y和z轴方向对转子产生的悬浮力；Fbx和Fby分别为2-DOF BPMSM在x和y轴方向对转子产生的悬浮力；la和lb分别为3-DOF HMB和2-DOF BPMSM所在位置到转子质心平衡位置的距离；ω为转子角速度；Te为电磁转矩；TL为负载转矩。

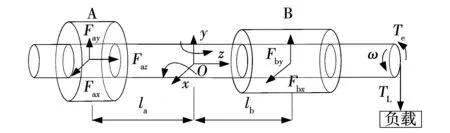
图2 5-DOF BPMSM刚性转子结构示意图Fig.2 Structure of the rigid rotor of the 5-DOF BPMSM

5-DOF BPMSM的悬浮力和电磁转矩数学模型[15-16]可以表示为：

(1)

式中：xa和xb分别为3-DOF HMB以及2-DOF BPMSM中转子在x轴方向的径向偏移；ya和yb分别为3-DOF HMB以及2-DOF BPMSM中转子在y轴方向的径向偏移；za为转子在z轴方向的轴向偏移；iax、iay和iaz为3-DOF HMB的控制电流；kir和kiz为电流刚度系数；kxy和kz为位移刚度系数；iBd和iBq、iMd和iMq分别为2-DOF BPMSM中悬浮力绕组在d-q坐标系中的电流分量以及转矩绕组在d-q坐标系中的电流分量；ψMd和ψMq分别为2-DOF BPMSM中转矩绕组和永磁体在d-q坐标系中的气隙磁链分量；K和kC为与电机结构相关的常数。

1.3 5-DOF BPMSM运动方程

在建立5-DOF BPMSM运动方程时，将转子看作刚体，同时考虑5-DOF BPMSM系统的陀螺效应以及转子五个自由度方向之间的耦合影响，建立的方程为：

(2)

式中：x=lbxa/(la+lb)+laxb/(la+lb)、y=lbya/(la+lb)+layb/(la+lb)和z=za分别为转子质心平衡位置在x、y和z轴方向上偏离O点的位移；m为转子质量；Jx、Jy和Jz分别为转子绕x、y和z轴的转动惯量且满足Jx=Jy=JQ；θx=(yb-ya)/(la+lb)和θy=(xa-xb)/(la+lb)分别是转子在xOz平面和yOz平面的转角。

1.4 可逆性分析

选取5-DOF BPMSM的状态变量为

X=(x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11)T=

(3)

输入变量为

U=(u1,u2,u3,u4,u5,u6,u7)T=

(iax,iay,iaz,iMd,iMq,iBd,iBq)T。

(4)

输出变量为

Y=(y1,y2,y3,y4,y5,y6)T=

(xa,ya,za,xb,yb,ω)T。

(5)

将式(1)以及式(3)～式(5)代入式(2)可以得出5-DOF BPMSM系统的11阶状态方程，再对输出变量Y进行求导，直至每一个分量都显含输入变量U，得出：

(6)

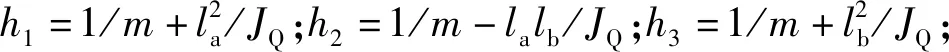
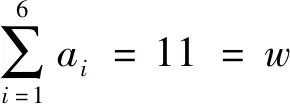
U=[u1,u2,u3,u4,u5,u6,u7]T=

(7)

2.1 T-S型模糊神经网络结构及工作原理

T-S型模糊神经网络不仅具有神经网络出色的非线性逼近能力，而且具有T-S型模糊推理系统出色的模糊信息处理能力，同时两者的特性互补，使得T-S型模糊神经网络相较于神经网络，在对非线性系统输入输出的表达能力方面有了明显提高。

图3为多输入多输出的T-S型模糊神经网络结构图，由图可见，T-S型模糊神经网络由前件网络和后件网络两部分组成。其中，前件网络共4层，用于匹配模糊规则前件；后件网络共3层，用于推理生成模糊规则后件。每一层的算法及数据处理过程如下：

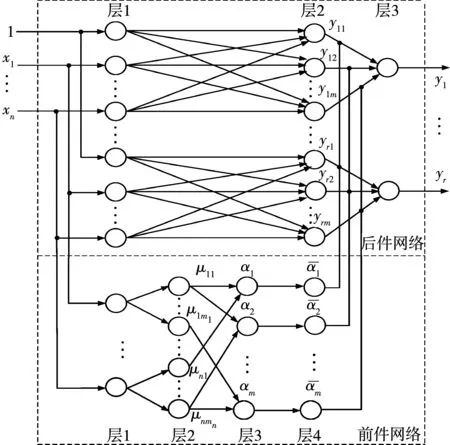
图3 T-S型模糊神经网络结构图Fig.3 Structure of the T-S fuzzy neural network

前件网络中，第一层为输入层，其中的每个节点都与输入分量相连，把输入量x=[x1,x2,…,xn]T传递到下一层。

第二层的每个节点都代表一个模糊量，作用是计算每个输入分量xi属于各模糊量的隶属度函数值。若选用高斯型函数作为隶属度函数，则有

(8)

式中：i=1,2,…,n；j=1,2,…,mi；n和mi分别为输入量x的维数和输入分量xi的模糊分割数；cij和bij为前件网络参数，分别代表高斯型函数的中心值和宽度值，需要在训练中确定。

第三层的每个节点都代表一条模糊规则，其作用是用来匹配模糊规则的前件，计算出每条规则的适应度αk，计算公式为

αk=μ1i1μ2i2…μnin。

(9)

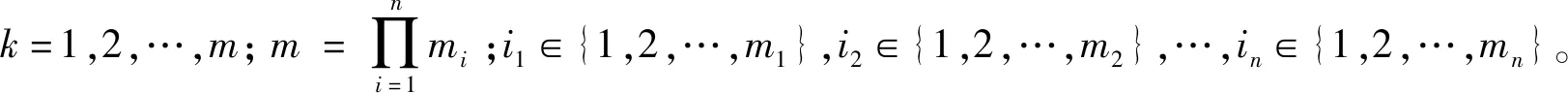
第四层是归一化层，计算公式为

(10)

后件网络中，第一层也为输入层，第一个节点的输入为1，用于提供模糊规则的后件常数项。

第二层的每个节点都对应一条模糊规则，用于计算每条模糊规则的后件输出，表达式为

(11)

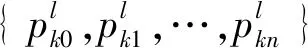
第三层是计算T-S型模糊神经网络的最终输出，公式为

(12)

2.2 逆系统的构建

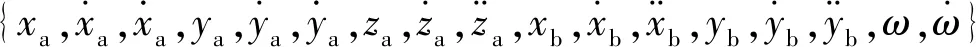
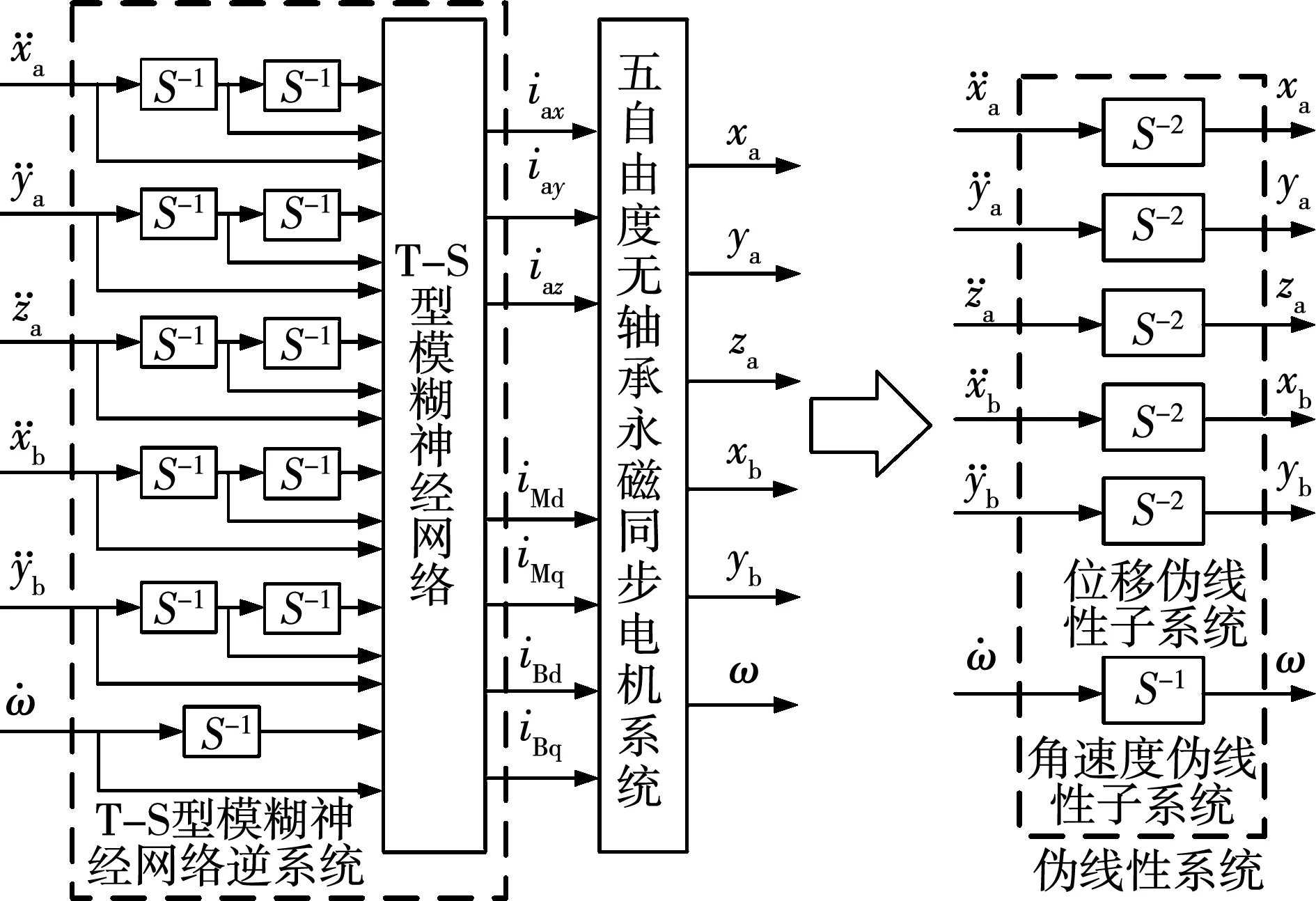
图4 伪线性系统Fig.4 Pseudo-linear system

2.3 附加闭环控制器的设计

在实际应用过程中，使用T-S型模糊神经网络来构建5-DOF BPMSM的逆系统必然存在一定的建模误差，因此，构建出的逆系统与5-DOF BPMSM系统复合而成的伪线性系统并不是理想的线性系统，必须设计附加闭环控制器才能使系统获得优良的动静态特性，并且考虑到电机运行过程中的参数变化以及受到的不确定干扰，设计了自抗扰控制器对伪线性系统进行综合。传统的自抗扰控制器包含扩张状态观测器(extended state observer, ESO)、跟踪微分器(tracking differentiator, TD)以及非线性状态误差反馈控制率(nonlinear state error feedback law, NLSEFL)三个模块，其控制思想为ESO模块将系统受到的内外扰动看作扩展状态加以观测，并通过NLSEFL模块加以补偿，使系统具有较强的抗干扰能力。

对解耦后得到的二阶位移伪线性子系统设计传统的二阶自抗扰控制器，其算法为：

(13)

非线性函数为：

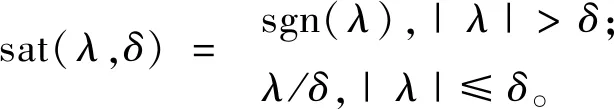
(14)

(15)

式中：v为给定输入；y为被控对象的输出；v1和v2分别为给定输入v的跟踪信号及微分信号；z1和z2为被控对象的状态变量，z3为总扰动的实时作用值；R、δ11、δ12、δ13、α11、α12、α13、α14、α15、β11、β12、β13、k11、k12和b11为二阶自抗扰控制器参数。

同样地，对解耦后得到的一阶角速度伪线性子系统设计一阶自抗扰控制器。针对传统自抗扰控制器调节参数多、算法复杂的问题，采用如图5所示的结构优化的一阶自抗扰控制器对角速度伪线性子系统进行综合。由于传统的一阶自抗扰控制器中TD模块的输出不含微分信号，所以在结构优化的一阶自抗扰控制器中省去了不必要的TD模块。同时，用线性比例调节器P代替NLSEFL模块，并在ESO模块中使用线性反馈代替部分的非线性反馈。

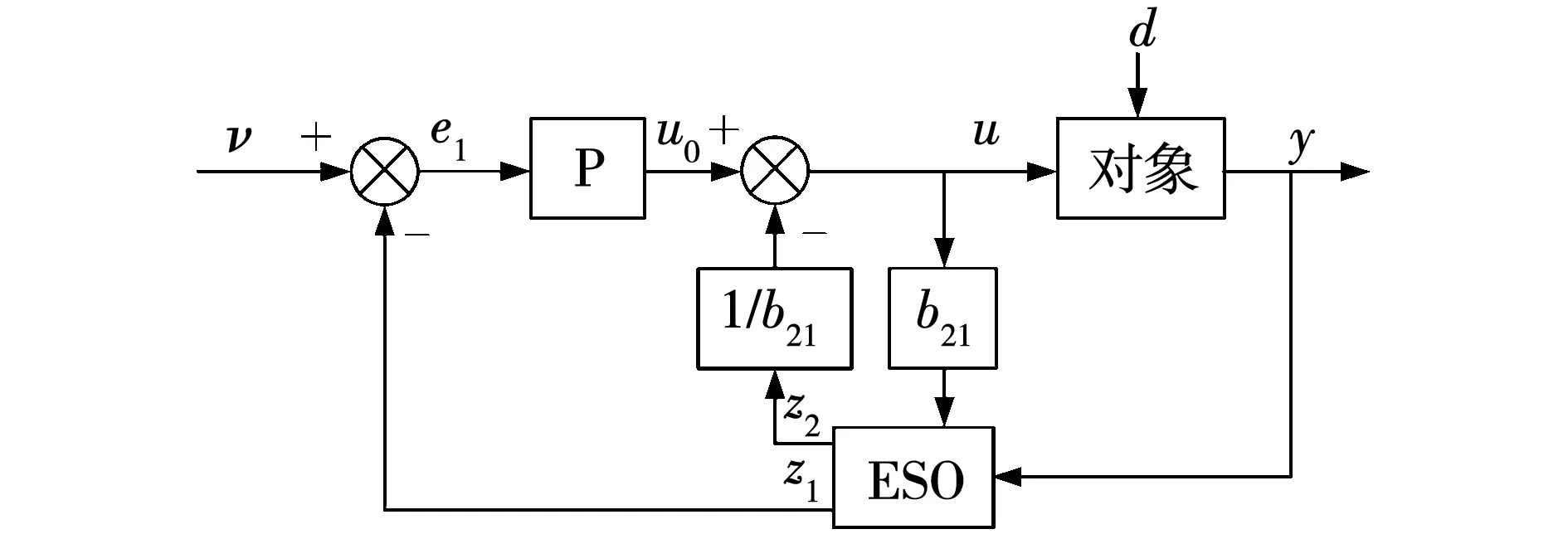
图5 结构优化的一阶自抗扰控制器结构框图Fig.5 Diagram of the optimized 1-order active disturbance rejection controller

结构优化的一阶自抗扰控制器算法为：

(16)

式中：δ21、α21、β21、β22、kP21和b21为结构优化的一阶自抗扰控制器参数；其他参数意义同上。

最终，可以构建出基于T-S型模糊神经网络逆系统的5-DOF BPMSM自抗扰控制系统，其控制框图如图6所示。

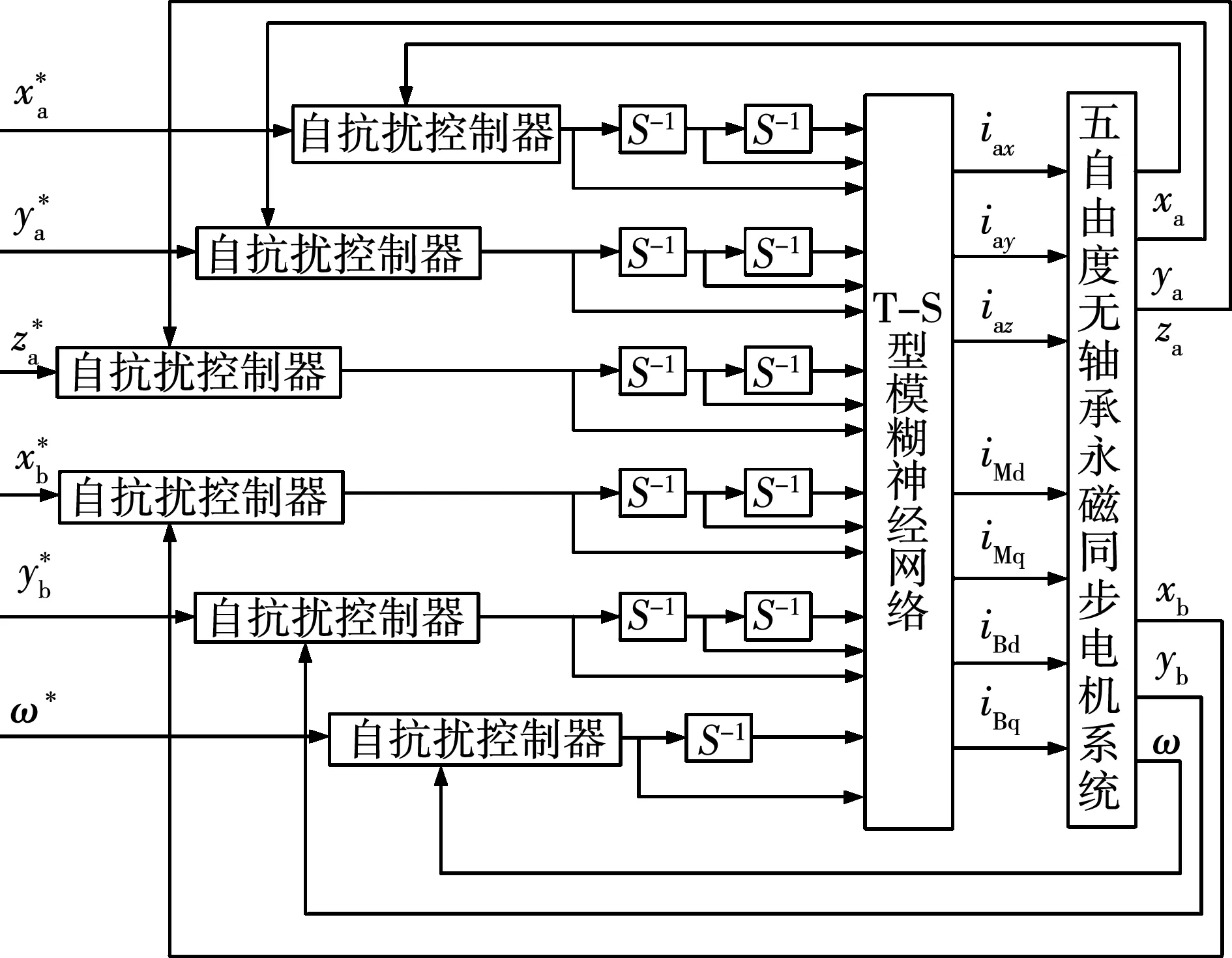
图6 所提控制方法框图Fig.6 Block diagram of the proposed control method

3.1 仿真研究及结果分析

为了验证所提控制方法的有效性，以5-DOF BPMSM为研究对象，将提出的基于T-S型模糊神经网络逆系统的自抗扰控制方法与传统的基于逆系统的PID控制方法在MATLAB/Simulink环境下进行对比仿真研究。

仿真中，转子的初始位置为xa=xb=x=-0.3 mm，ya=yb=y=-0.4 mm，z=za=-0.2 mm。2-DOF BPMSM的参数为：转矩绕组极对数PM=1，电阻RM=2.316，电感LM=0.013 42 H；悬浮力绕组极对数PB=2，电阻RB=1.85，电感LB=0.002 34 H；永磁体磁链ψf=0.473 Wb。3-DOF HMB的参数为：kiz=1 057.89 N/A，kz=-1.793×107N/m，kir=863.76 N/A，kxy=4.602×106N/m。转子参数为：质量m=1.6 kg。

位移伪线性子系统的自抗扰控制器参数为：R=200，δ11=0.01，α11=0.75，α12=0.5，α13=0.25，b11=1.2，δ12=0.01，β11=15 000，β12=140 000，β13=1 100，α14=1.25，α15=0.75，δ13=0.05，k11=210，k12=0.15；角速度伪线性子系统的自抗扰控制器参数为：β21=960，β22=1 700，α21=0.5，δ21=0.01，kP21=25，b21=0.5；经过参数优化整定获得的位移伪线性子系统的PID控制器参数为：kP1=200，kI1=0.15，kD1=0.3；经过参数优化整定获得的角速度伪线性子系统的PID控制器参数为：kP2=7，kI2=0.1。

图7为转子起浮性能对比仿真曲线。由图可见，若采用基于逆系统的PID控制方法，转子经过大约66 ms的振荡后可以在平衡位置稳定悬浮，而在提出的基于T-S型模糊神经网络逆系统的自抗扰控制方法下，只需34 ms左右，转子就可以在平衡位置稳定悬浮。同样可见，在提出的控制方法下，转子的振荡幅值明显小于采用基于逆系统的PID控制方法时转子的振荡幅值。对比仿真结果表明在所提控制方法下，系统具有更好的转子起浮性能。

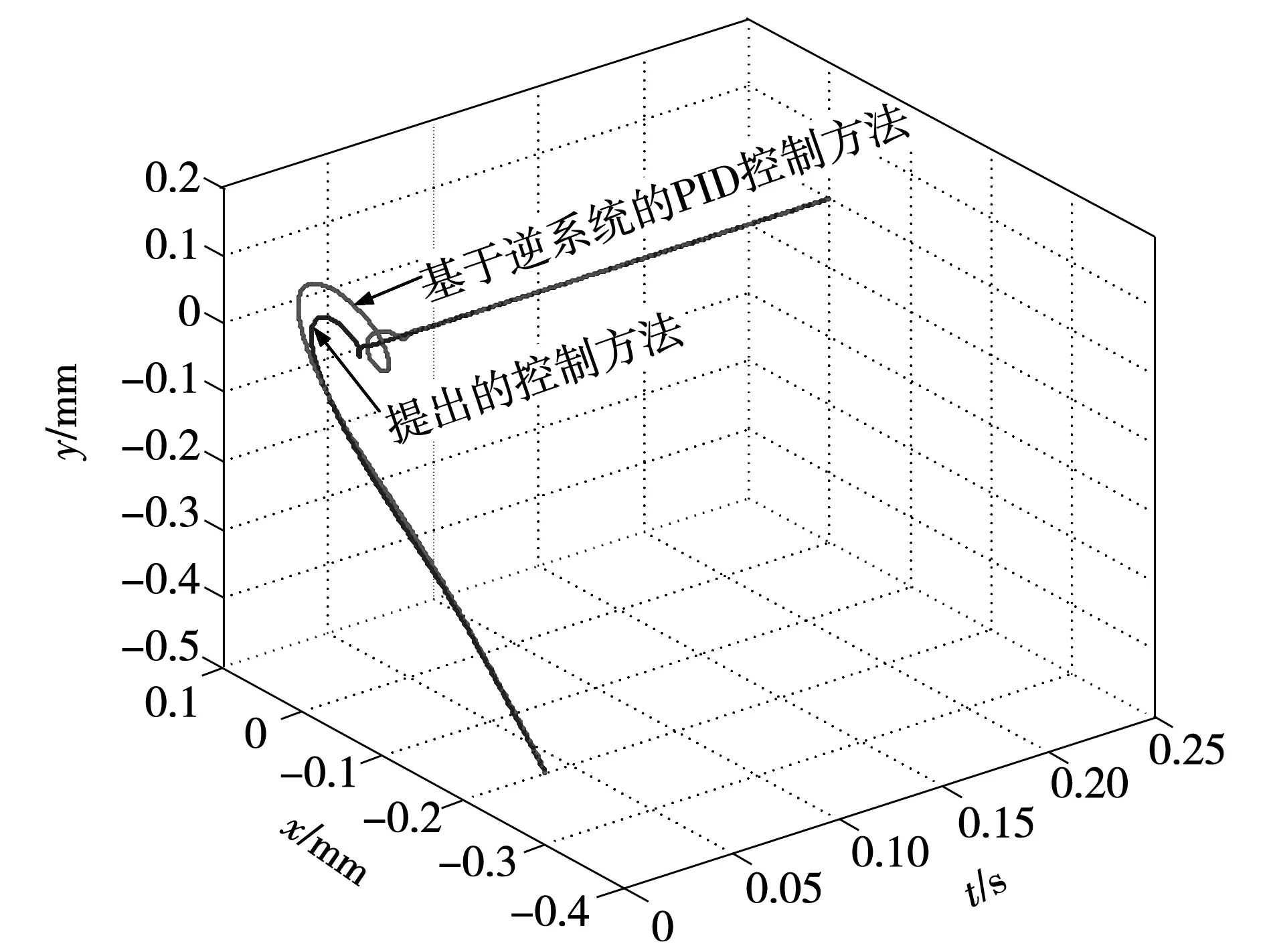
图7 起浮性能对比仿真曲线Fig.7 Comparative simulation curves of the floating performance

图8为抗干扰性能对比仿真曲线。当转子稳定悬浮运行后，依次在0.1、0.15和0.2 s时分别沿x、y和z轴方向给转子施加30 N的干扰力。由图8(a)～图8(c)可见，在基于逆系统的PID控制方法下，转子在x、y和z轴方向上波动的峰值分别约为49、40和37 μm，而在提出的基于T-S型模糊神经网络逆系统的自抗扰控制方法下，转子在x、y和z轴方向上波动的峰峰值分别减小为33、27和19 μm，且转子恢复稳定悬浮的调节时间也明显小于采用基于逆系统的PID控制方法时的调节时间。对比仿真结果表明在所提控制方法下，系统具有更强的鲁棒性。

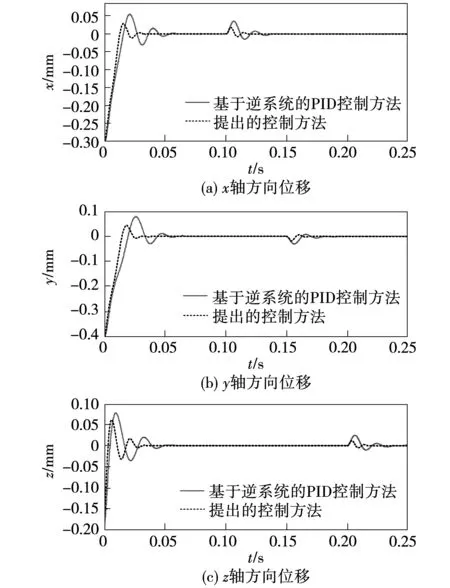
图8 抗干扰性能对比仿真曲线Fig.8 Comparative simulation curves of the anti-interference performance

图9为悬浮力与电磁转矩的解耦性能对比仿真曲线。t=0.125 s时，将给定转速由2 000 r/min突变为3 000 r/min。由图可见，在基于逆系统的PID控制方法下，转速经过34 ms左右的调节时间达到3 000 r/min，在此过程中，转速响应产生了40 r/min的超调量，同时在转速突变过程中，转子在x和y轴方向上波动的峰峰值分别为28和36 μm，转子在z轴方向的位移几乎未受转速变化的影响，而在提出的基于T-S型模糊神经网络逆系统的自抗扰控制方法下，转速仅经过约24 ms的调节时间就可几乎无超调的达到3 000 r/min，并且转子在x、y以及z轴方向的位移都没受到转速突变的影响。对比仿真结果说明提出的控制方法具有更快、更精确的转速调节性能，并且更好地实现了电磁转矩与悬浮力之间的解耦控制。

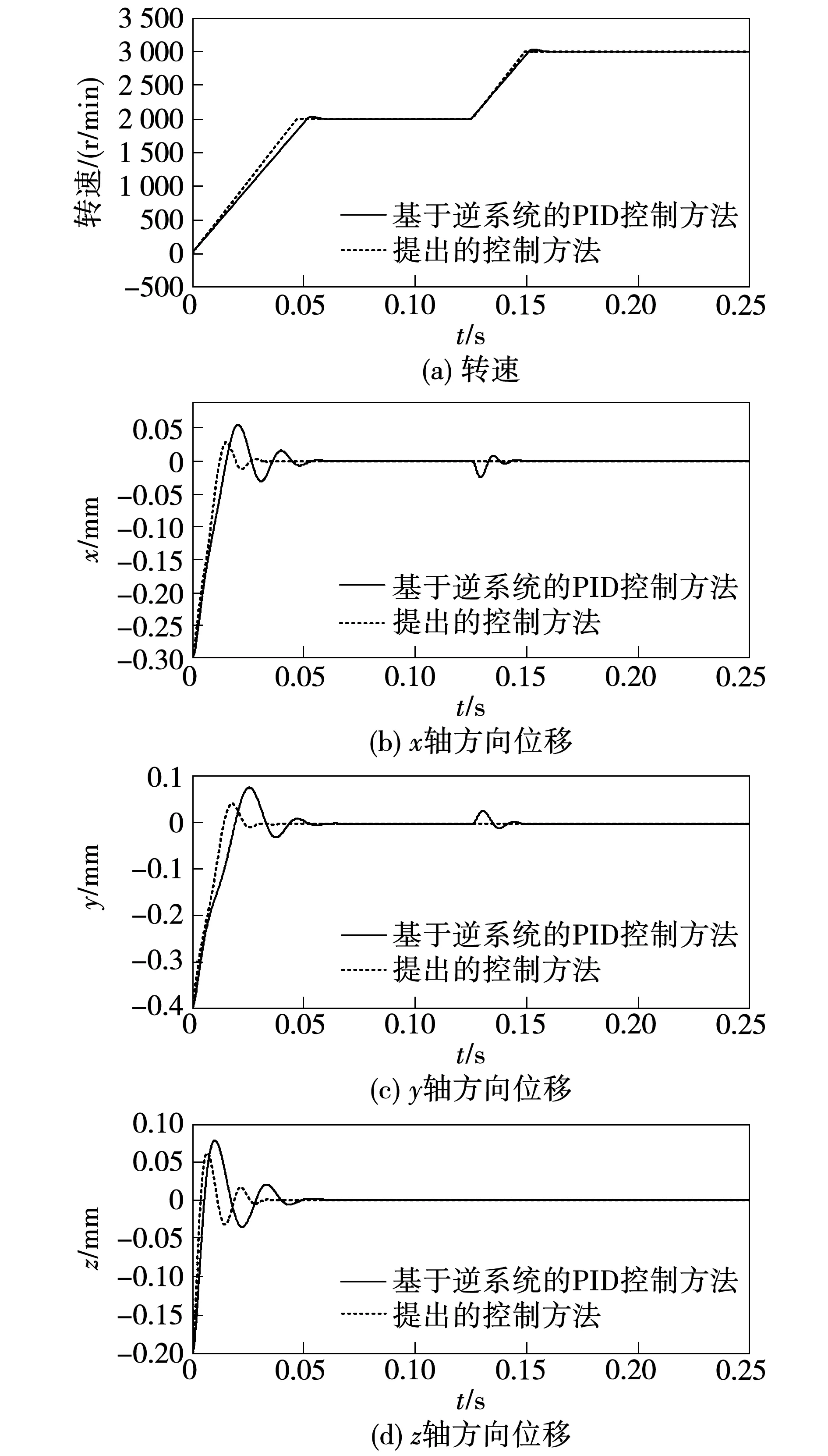
图9 悬浮力与电磁转矩的解耦性能对比仿真曲线Fig.9 Comparative simulation curves of the decoupling performance between the suspension forces and the electromagnetic torque

图10为悬浮力之间的解耦性能对比仿真曲线。转子在平衡位置稳定悬浮运行后，在t=0.1 s时对位移xa给定信号施加一个幅值为0.1 mm的阶跃信号。

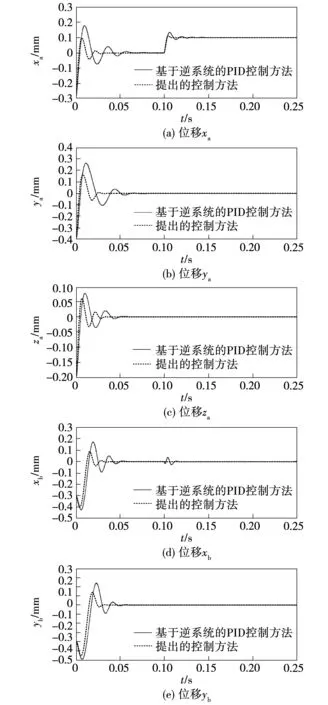
图10 悬浮力之间解耦性能对比仿真曲线Fig.10 Comparative simulation curves of the decoupling performance between suspension forces

由图10(a)可见，若采用基于逆系统的PID控制方法，位移xa经过45 ms的调节时间可稳定到达0.1 mm，同时由图10(b)～图10(e)可见，位移ya、位移za以及位移yb均未受到位移xa变化的影响，而同为x轴方向的位移xb受位移xa变化的影响产生了峰峰值为67 μm的波动，而采用基于T-S型模糊神经网络逆系统的自抗扰控制方法时，从图10(a)可以看出，位移xa只需8 ms左右的调节时间，就可几乎无超调的到达0.1 mm处，同时由图10(b)～图10(e)可见，位移xa的变化对转子其他四个自由度的位移信号都未产生影响。对比仿真结果说明提出的控制方法具有更快的位移调节性能，并且更好地实现悬浮力之间的解耦控制。

3.2 实验研究及结果分析

使用一台2-DOF BPMSM样机进行提出的基于T-S型模糊神经网络逆系统的自抗扰控制方法与传统的基于逆系统的PID控制方法的对比实验研究，样机主要参数如表1所示。采用DSP TMS320F28335作为数字控制器，完整的实验平台如图11所示。

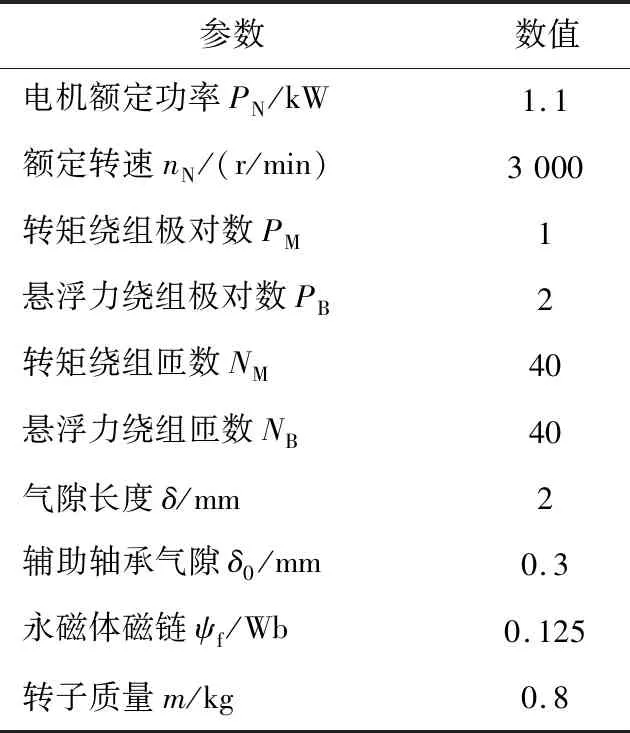
表1 2-DOF BPMSM参数表Table 1 Parameters of the 2-DOF BPMSM

图11 2-DOF BPMSM实验平台Fig.11 Experimental platform of the 2-DOF BPMSM

图12为速度变化时两种不同解耦控制方法的对比实验波形。由图12(a)可知，在基于逆系统的PID控制方法下，电机转速从1 000 r/min上升到3 000 r/min的调节时间为120 ms，在转速上升过程中，转速产生了300 r/min左右的超调量，转子在x和y轴方向上波动的峰峰值分别为60和64 μm；相比于基于逆系统的PID控制方法，在提出的基于T-S型模糊神经网络逆系统的自抗扰控制方法下，转速可以几乎无超调的上升到3 000 r/min，并且转速的调节时间减少了29.2%，同时在转速变化过程中，转子在x和y轴方向上波动的峰峰值也分别减少了25%和21.9%。对比实验结果表明，提出的控制方法具有更好的调速性能，并且更好地实现了电磁转矩与悬浮力之间的解耦控制。

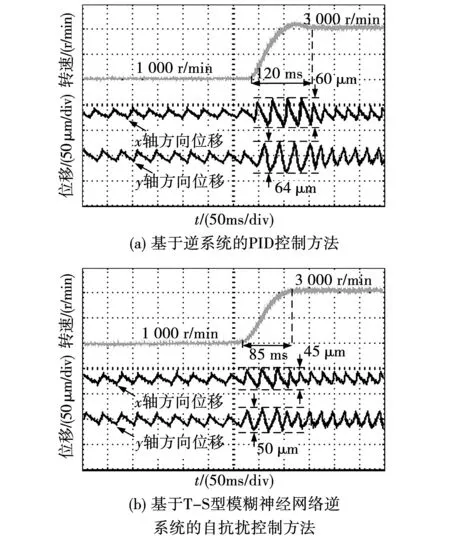
图12 速度变化的对比实验波形Fig.12 Comparative experiment waveform with speed variation

图13为干扰力作用下两种不同解耦控制方法的对比实验波形。当电机以3 000 r/min的转速在平衡位置稳定悬浮运行时，沿y轴方向突加一个20 N的干扰力。由图13(a)可知，当采用基于逆系统的PID控制方法时，在干扰力作用下，转子在y轴方向上偏离了平衡位置48 μm，由于耦合影响，转子在x轴方向上也偏离了平衡位置34 μm，并且转子经过115 ms的调整后可重新在平衡位置稳定悬浮。当采用提出的基于T-S型模糊神经网络逆系统的自抗扰控制方法时，从图13(b)可以很明显看出，在干扰力作用下，转子在y轴方向上的偏移量为43 μm，转子受耦合影响在x轴方向上的偏移量为19 μm，并且转子恢复稳定悬浮的调节时间为89 ms。对比实验结果表明提出的控制方法可以使系统具有更强的抗干扰能力，并且能够更好地实现悬浮力之间的解耦控制。

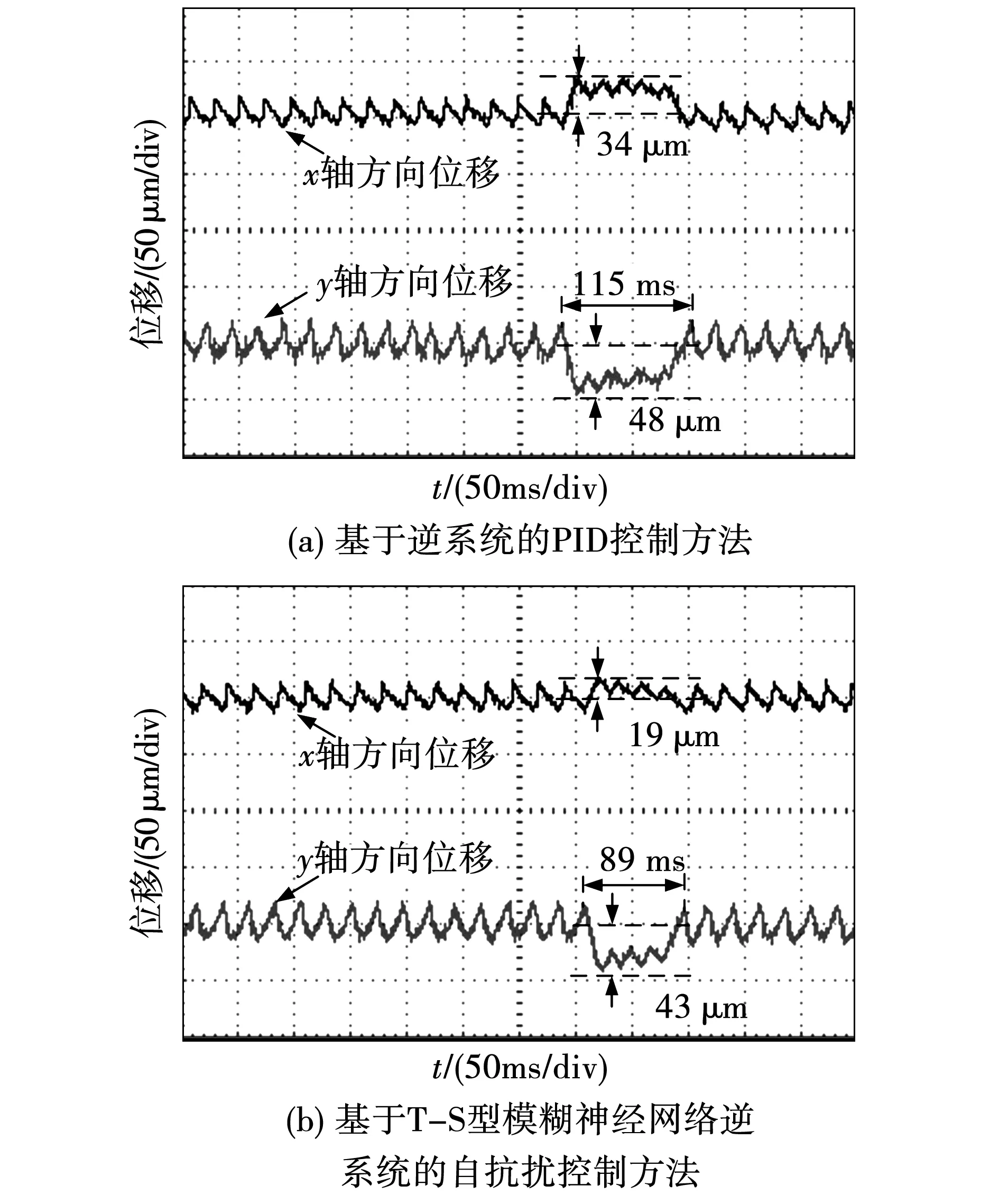
图13 干扰力作用下的对比实验波形Fig. 13 Comparative experiment waveform with interference force

本文提出了一种基于T-S型模糊神经网络逆系统的自抗扰控制方法来实现5-DOF BPMSM的解耦控制。首先，利用T-S型模糊神经网络出色的非线性逼近能力构建出5-DOF BPMSM的逆系统，并将构建的逆系统与5-DOF BPMSM串联，使非线性的5-DOF BPMSM解耦为6个伪线性子系统；然后，考虑到伪线性子系统的特点，设计了自抗扰控制器来保证伪线性子系统的稳定性；最后，通过仿真和实验对所提控制方法的有效性进行了验证。结果表明，本文提出的控制方法具有更好的解耦性能，更高的控制精度，更快的响应速度以及更强的抗干扰能力。此外，本文提出的控制方法也为其他无轴承电机的解耦控制提供了参考。