一种新型的双输入双向DC-DC变换器

赵世伟，沈超

(华南理工大学 电力学院，广州 510641)

0 引 言

双向DC-DC变换器作为平衡直流母线电压的重要装置在直流微电网中得到广泛应用[1-4]。在其控制方式上，移相控制由于具有控制简单、易于实现软开关、双向切换便利等优势，一直是国内外研究的重点。在基本移相控制的基础上，现已提出双重移相控制、三重移相控制、混合移相控制等多种移相控制方式[5-8]。控制方式的改进也使得变换器的回流功率和电流应力降低，提升了变换器性能[9-11]。但上述多种控制方式大多是基于双有源桥式变换器(dual active bridge，DAB)提出的，在其他拓扑上应用较为困难。故如何在非DAB的双向DC-DC变换器上实现双重移相的控制效果值得深入探究。

文献[12]通过将基本元件进行不同的组合构造了一系列的方波电压源，并将其加在变压器的原副边，从而得到不同的双向DC-DC变换器。文献[13]在文献[12]的基础上，通过改变原副边开关管的占空比外加移相控制，在输入输出电压不匹配时，减小了电流应力，扩大了软开关的范围。虽然二者的结构相较DAB更加简单，但其无功功率仍然较大，电流应力较高。文献[14]通过在原边全桥引入内移相角使得无功回流减小，电流应力下降，提升了变换器的效率，但其只适合于全桥结构。文献[15]在双向全桥变换器的基础上加入了多输入结构，虽然利用全桥实现了双重移相的控制方式，但其开关管总数过多，结构复杂、效率较低。本文在文献[12]的基础上利用双输入结构直接在变换器原边构造出三电平的方波电压，从而降低了变换器的回流功率和电流应力。

对于具有大量储能单元的直流微电网系统，本文通过改变输入端结构增加一路输入源，构造出一种双输入双向DC-DC变换器。该变换器通过改变输入各开关管的占空比与移相角大小，能直接在变换器原边构造出三电平的方波电压，从而获得类似全桥电路双重移相下的电压波形。通过对变换器的工作原理以及功率特性进行分析可知，该变换器能有效降低回流功率和电流应力，相较于传统的单输入变换器而言，有效地提升了变换器的稳态性能。同时双电源输入使得原边方波电压幅值增大，在各开关管电压应力相同的情况下，提高了变换器所能传输的最大功率。

提出的双输入双向DC-DC变换器结构如图1所示。其中U1、U2分别表示两个储能单元的电压，且满足U1=U2；C为原边串联电容；L为变压器漏感及外加串联电感之和；n:1表示变压器变比。以功率由原边U1、U2传输到副边Uo为例进行分析，反向功率传输分析类似。

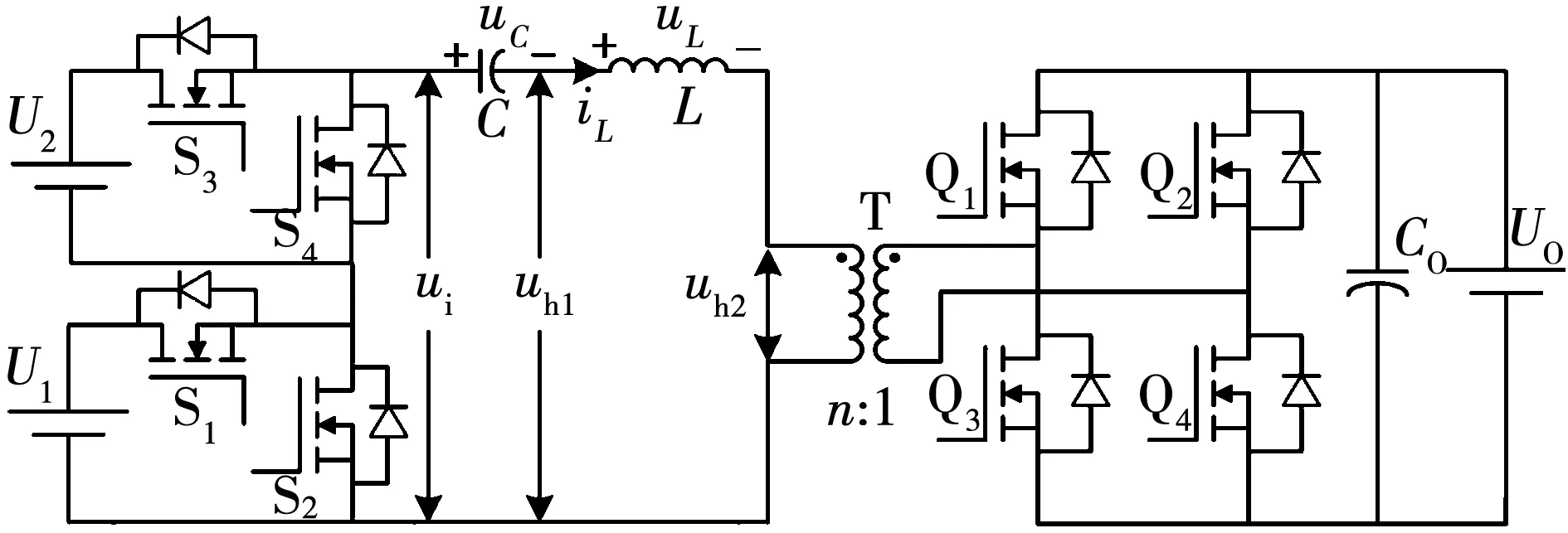
图1 双输入双向DC-DC变换器Fig.1 Dual input bidirectional DC-DC converter

传统的单输入半桥型双向DC-DC变换器(去掉U2和S3、S4短路，以只有电源U1为例)原边侧两个开关管互补导通，各导通180°，副边侧上下开关管互补导通180°，对角开关管同时导通，其工作波形如图2所示。其中：S1、S2、Q1～Q4表示对应开关管的驱动信号；ui表示输入电压；uC表示串联电容电压；uh1表示原边侧逆变电压；uh2表示副边折算到原边的逆变输出电压；uL表示变压器漏感及串联电感之和的电压；iL表示电感电流；T表示开关周期；Ths表示半个开关周期；φ表示半个开关周期内的移相比，1≥φ≥0。

从图2可以看出，在t1～t3时间段，电源将一半能量传输给电感L及副边Uo，一半能量储存在电容C中；在t4～t6时间段，储存在电容中的能量再释放给Uo；而在t3～t4时间段，电感L能量回馈给电容；在t0～t1时间段，回馈给电容的能量以及此时电感的能量共同向电源回馈，故会出现较大的回流功率，使得电流应力增大。

在原边逆变电压uh1波形中引入内移相角能减小回流功率，可以通过添加一路输入，并在一个开关周期中对两个电源的接入断开进行合理控制来实现该特性。电路如图1所示，其中S1、S2互补导通，S3、S4互补导通，S1导通占空比为D1，S3导通占空比为D2，且满足1≥D1≥0.5≥D2≥0。变换器工作波形如图3所示。其中φ1、φ2同全桥电路一样，表示半个开关周期内的移相比，分别定义为内移相比和外移相比，1≥φ2≥φ1≥0。图3中其他变量定义与图2一致。从图3中可以看出，电感向电源回流的功率减小，电感电流应力降低。

图2 单输入变换器工作波形Fig.2 Operating waveform of single input converter

为简化电路分析，可做如下假设：1)变换器已达稳态工作；2)MOSFET为理想开关器件，不考虑其寄生参数；3)变压器励磁电感足够大，励磁电流可以忽略；4)串联电容C和输出电容Co的电容量足够大，其两端电压纹波可以忽略。该变换器在一个开关周期T内共有8个开关模态，每个模态等效电路如图4所示，主要原理波形如图3所示，主要工作过程描述如下。

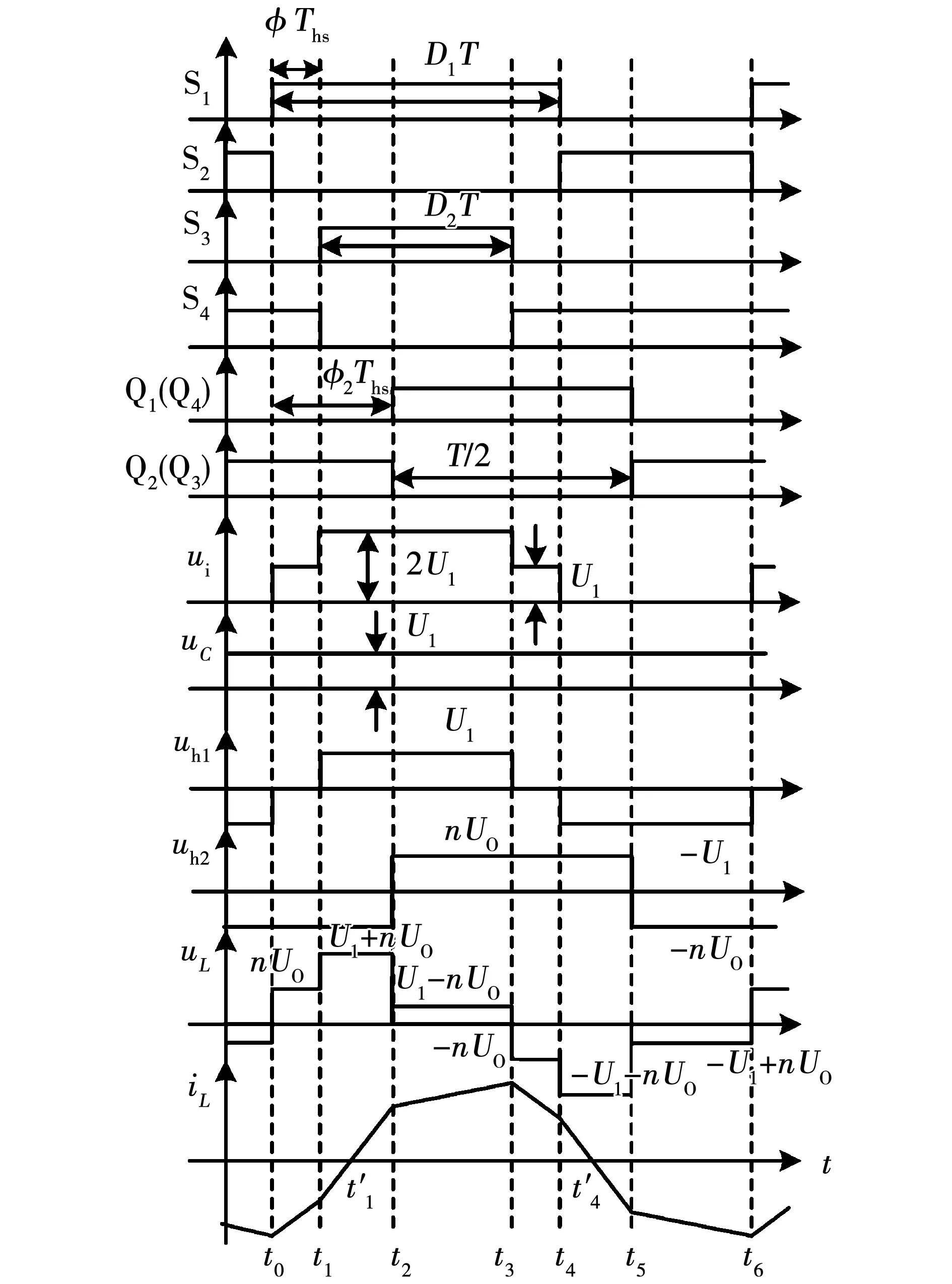
图3 双输入变换器工作波形Fig.3 Operating waveform of dual input converter

1)模态1：t0～t1阶段。

工作状态如图4(a)所示。在t0时刻之前，原边侧开关管S2、S4导通，S1、S3关断，副边侧开关管Q2、Q3导通，Q1、Q4关断，电流为负；在t0时刻，开关管S1导通、S2关断，此时电流仍然为负，因为串联电容C的电压等于电源U1的电压，故uh1电压为0，相当于短路。在该时间段，电感L中的能量只通过副边侧Q2、Q3给Uo供电，电流逐渐减小，原边侧只有串联电容C向U1回馈能量。电感L的电流可以表示为

(1)

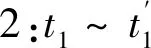
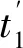
(2)

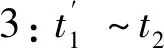
4)模态4：t2～t3阶段。

工作状态如图4(d)所示。在t2时刻，副边开关管Q1、Q4导通，Q2、Q3关断。原边侧电源U1、U2给电容C以及电感L充电的同时，通过副边侧开关管Q1、Q4给Uo供电。此阶段为该半个周期中原边侧向副边侧传输能量的主要阶段。电感L的电流可以表示为

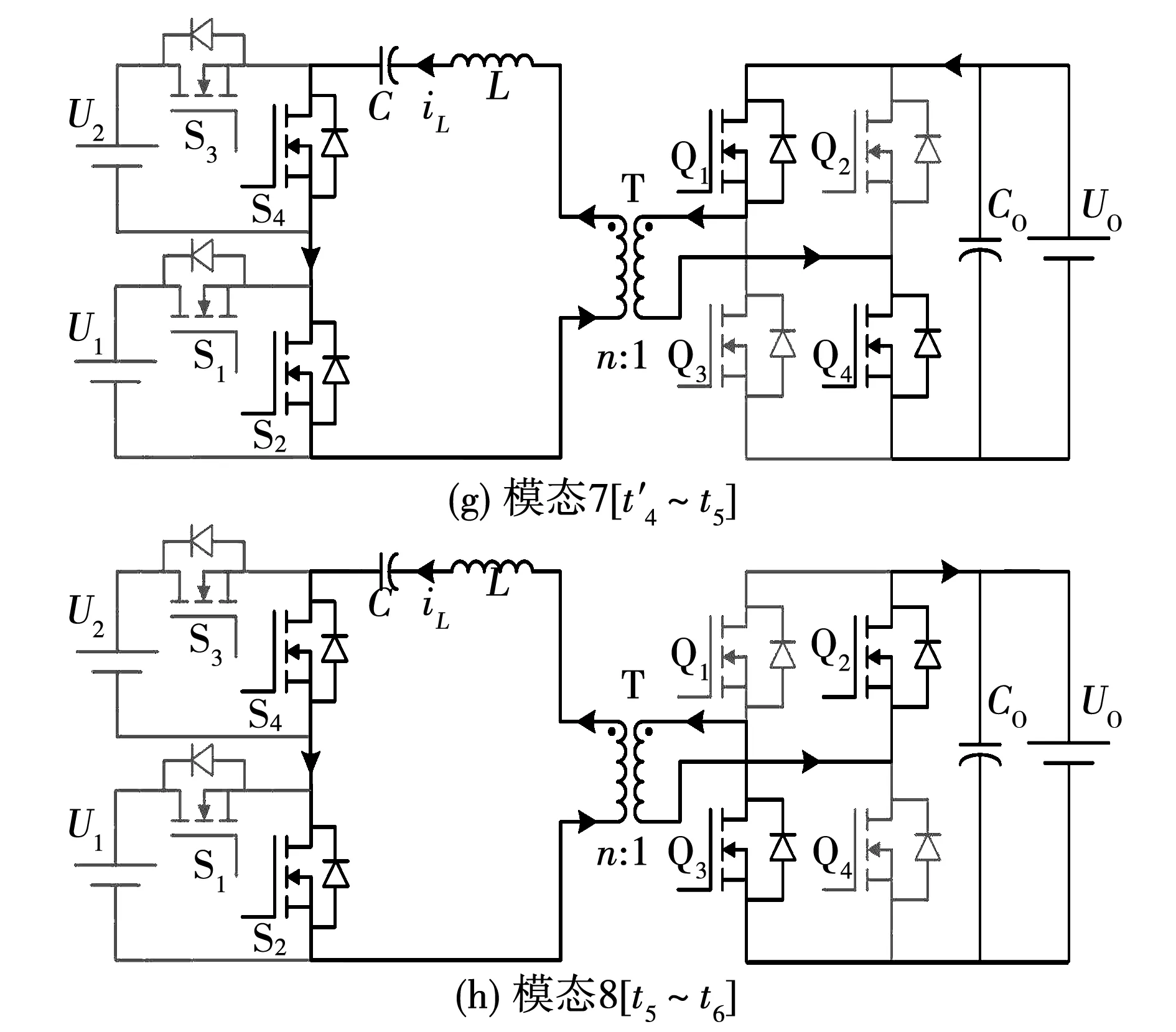
图4 不同工作模态的等效电路Fig.4 Equivalent circuits with different operating modes

(3)

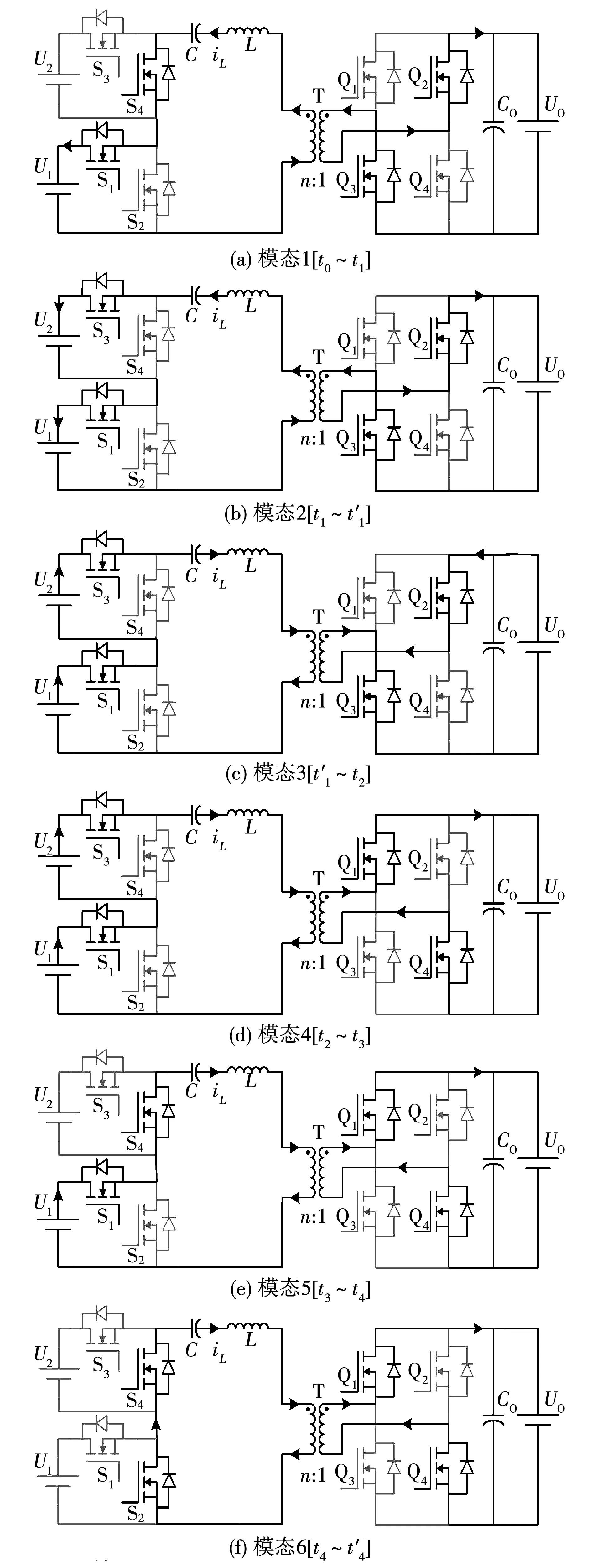
5)模态5：t3～t4阶段。

工作状态如图4(e)所示。在t3时刻，开关管S4导通，S3关断，电流保持为正。由于电容C的电压等于电源U1电压，故uh1电压为0，相当于短路。此阶段原边侧可看成电源只给电容在充电，电感L中的能量继续通过副边的Q1、Q4传递给Uo，电流逐渐降低。电感L的电流可以表示为

(4)

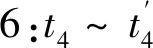
工作状态如图4(f)所示。在t4时刻，开关管S1关断，S2导通，原边电源均断开，此时电流仍然为正。电感L的能量一部分回馈给串联电容C，一部分通过副边开关管Q1、Q4给Uo供电，电流快速减小。电感L的电流可以表示为

(5)

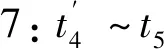
8)模态8：t5～t6阶段。

工作状态如图4(h)所示。在t5时刻，副边开关管Q1、Q4关断，Q2、Q3导通，此时电流为负。此阶段原边侧电源依旧断开，电容C中存储的能量通过S2、S4释放，给电感L充电的同时，通过副边侧开关管Q2、Q3给Uo供电。电感L的电流可以表示为

(6)

2.1 两电源输出功率分析

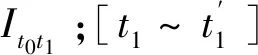
表1 一个开关周期中能量流动情况Table 1 Energy flow in a switching cycle

对于储能单元U1，其输出功率为

(7)

储能单元U2输出功率为

(8)

可以看出两个电源的输出功率大小相等，均等分担负载所需功率。故在负载功率一定时，该双输入变换器每一个电源输出功率只有单输入变换器电源输出功率的一半，减小了储能单元的压力。

2.2 传输功率数学模型及范围

在图3中，t1=φ1Ths、t2=φ2Ths、t3=Ths、t4=(1+φ1)Ths、t5=(1+φ2)Ths；定义k=U1/(nUo)为电压调节比，k≥1；开关频率f=1/T=1/(2Ths)。其中：外移相比φ2是副边Q1管与原边S1管驱动信号之间的角度占比；内移相比φ1是电压波形uh1在半个周期内幅值为0的角度占比。φ1主要通过改变两个电源导通的占空比D1、D2来控制。其满足关系

φ1=D1-D2。

(9)

同时D1、D2满足约束条件：

(10)

通过调节D1、D2以及φ2来控制变换器传输功率的大小和方向，为了分析计算方便，下面对变换器功率的分析利用φ1、φ2来表示。

由式(1)～式(6)以及电感电流对称性可得一个开关周期中电感电流iL的表达式为：

(11)

由于电容C作为储能元件，本身并不消耗能量，所以电源向Uo传递的功率可以表示为

(12)

而对于单输入变换器，移相比φ=0.5时变换器有最大传输功率为

(13)

以该功率对双输入变换器的传输功率进行标幺化可得

(14)

根据该式可得传输功率与内外移相比的关系曲线如图5所示。

图5 传输功率与内外移相比的关系曲线Fig.5 Relation curve between the transmitted power and the internal and external shift

从图5中可以看出，当φ1=0、φ2=0.5时，该双输入变换器有最大传输功率为

(15)

从上述分析中可以看出，若要使得单输入变换器的最大传输功率与双输入变换器一致，需要将输入电压增大至2U1，但此时两个开关管所承受的电压应力也会增大至2U1，是双输入变换器开关管承受电压应力U1的2倍。故在开关管承受电压应力相同的情况下，该双输入变换器所能传输的最大功率是单输入变换器的2倍，扩大了功率传输范围。

2.3 回流功率比较分析

从能量流动的情况来看，对于单输入结构，在[t0～t1]及[t3～t4]时间段，电感储能在向电源回馈，故电源需向Uo传递更多的能量，从而使得电流应力更大，变换器效率更低；而对于双输入结构，在[t0～t1]及[t3～t4]时间段，uh1相当于短路，电感不需要向电源回馈能量，回流功率更小。

想要比较2种变换器的回流功率大小，需保证2个变换器传输功率的能力相同，即最大传输功率相同。为此，可假设单电源输入结构时，电源电压为2U1，此时其最大传输功率与双输入变换器相等。同时，需要在同一传输功率下对两种变换器的回流功率进行比较。

双输入变换器回流功率标幺值为

(2φ2-2φ1-1)]2。

(16)

单输入变换器回流功率标幺值为

(17)

图6给出了在3个不同电压调节比k下，传输功率标幺值P*分别取0.5、0.7、0.8时，2种变换器的回流功率情况。其中虚线表示单输入变换器对应的回流功率大小；实线表示双输入变换器在不同移相比取值组合下的回流功率曲线。

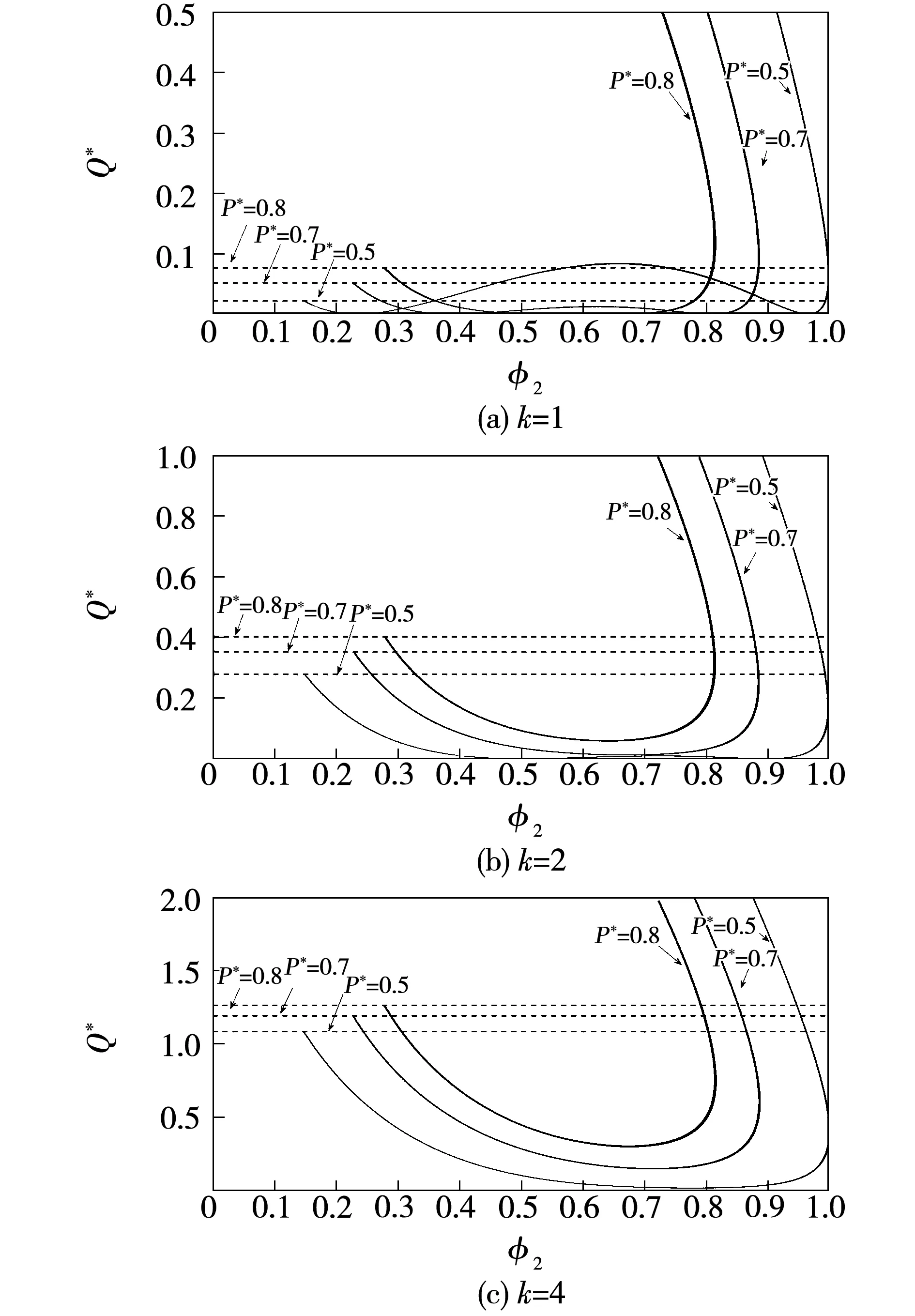
图6 回流功率关系曲线Fig.6 Relation curve of backflow power

从图6中可以看出，对于同一传输功率，双输入变换器不同的移相比组合产生的回流功率大小不同，通过对移相比的调节可以使得其回流功率比单输入变换器更小。而且2种变换器的回流功率均随电压调节比k的增大而增大，同时双输入变换器降低回流功率的效果也越明显。

以STM32F103RCT6为控制核心搭建了最大功率200 W的实验样机。样机参数如表2所示。实验平台如图7所示，由控制板和主功率板构成。

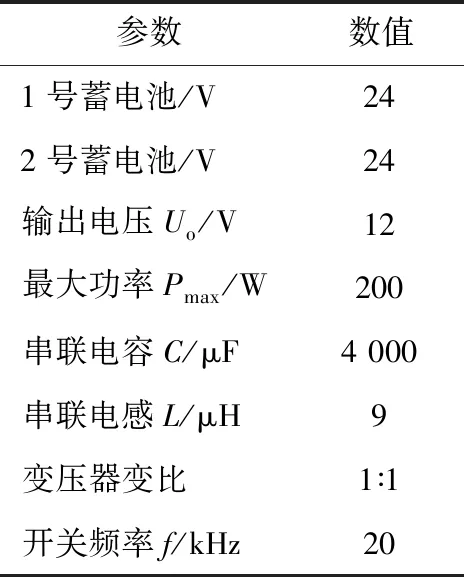
表2 实验参数Table 2 Experimental parameters

图7 实验平台Fig.7 Experiment platform

在实验中，通过固定内移相比，闭环调节外移相比来保证输出电压的稳定，具体控制框图如图8所示。

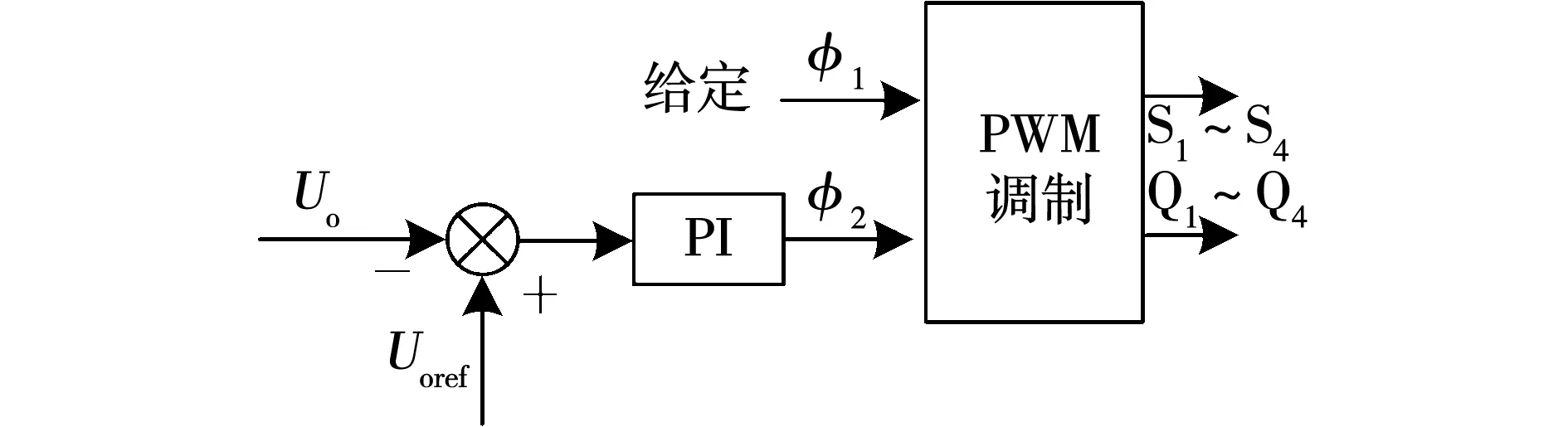
图8 控制框图Fig.8 Control block diagram

2个蓄电池电压均取24 V，控制输出电压为12 V，调节负载使得传输功率为100 W时，原边输入电压ui以及串联电容电压uC的波形如图9所示。可以看出，电容电压大小等于蓄电池电压24 V，输入电压波形为正的三电平方波。

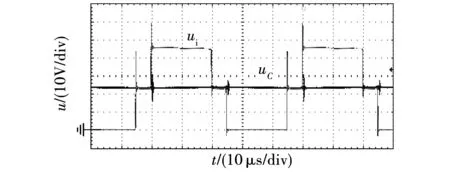
图9 串联电容电压波形Fig.9 Voltage waveform of series capacitor

在传输功率标幺值P*分别取0.5(100 W)、0.7(140 W)时，2种变换器的逆变电压uh1、uh2以及电感电流iL的波形如图10所示。可以看出，双输入变换器由于在uh1波形中存在一个内移相角，使得在同一传输功率下，其回流功率相较单输入变换器明显减小，同时其电流应力也有所降低。

图10 不同传输功率下两变换器实验波形Fig.10 Experimental waveforms of two converters at different transmission powers

不同传输功率下，两变换器电感电流峰值曲线如图11所示。可以看出，对于任一传输功率，双输入变换器的电流应力均比单输入变换器的更低，降低了磁芯元件以及开关管的开关损耗，提升了变换器性能。在传输功率接近于0或者最大时，由于此时内移相比的取值非常有限，而外移相比的取值与单输入非常接近，故对于回流功率与电流应力的优化并不明显。

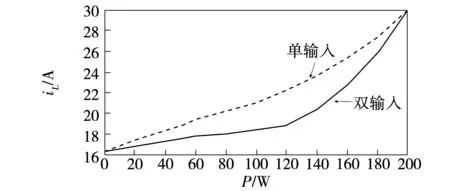
图11 不同传输功率下两变换器电流应力对比Fig.11 Comparison of current stress between two converters at different transmission power

两电源输入电流波形如图12所示，其中：i1表示蓄电池1的输出电流；i2表示蓄电池2的输出电流。可以看出，2个电源输出电流的大小基本一致，又因为两电源电压相同，故两电源输出功率相同，均等分担负载所需功率。

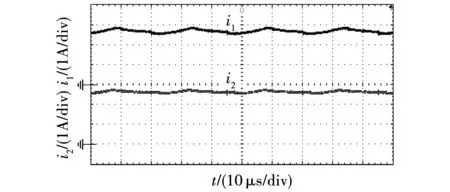
图12 两电源输入电流波形Fig.12 Input current waveforms of the two sources

本文设计了一款新型的双输入双向DC-DC变换器，理论分析和实验结果表明相对于单输入变换器，该变换器具有如下特点：

1)减小了回流功率和电流应力，使得变换器损耗减小、功率因数提高。

2)在开关管电压应力相同的情况下，提高了变换器的功率极限，扩大了功率传输范围。

3)该双输入变换器用于直流微网中能取代两个单输入变换器，简化了系统结构。