基于改进型DWA的移动机器人避障路径规划

卞永明，季鹏成，周怡和，杨 濛

（1.同济大学机械与能源工程学院，上海201804；2.交通运输部上海打捞局，上海200090）

路径规划是机器人智能化研究的重点方向之一。路径规划可以分为静态障碍物环境路径规划和动态障碍物环境路径规划，也可以分为侧重于路径最优的全局路径规划和侧重于安全避障的局部路径规划。在实现智能机器人的安全自主导航的要求下，局部路径规划是最有效的算法之一［1］。

动态窗口法（Dynamic Windows Approach，DWA）是Fox等［2］在曲率速度法（Curvature Velocity Method，CVM）［3］的基础上提出来的，实现了将移动机器人的位置约束问题转化为速度约束问题，将机器人的避障问题转化为最优速度执行问题。该算法充分考虑到移动机器人自身的机械特性的限制以及障碍物环境对速度的约束，根据约束形成动态窗口进行速度采样，并模拟采样速度一定时间内的速度生成待评价轨迹，结合评价函数对待评价轨迹评分，再选择其中评分最高轨迹对应的采样速度作为最优速度。通过该算法得到的路径在实现安全避障的同时充分考虑了机器人自身的运动特性，可靠性高，是局部路径规划中的常用算法。

Piyapat等［4］为了提高动态窗口法的安全性，扩大了动态窗口法评价函数考虑的障碍物范围，除了考虑待评价轨迹上的障碍物，同时考虑了该轨迹一定距离内的障碍物，提高了动态窗口法的避障性能，规避了机器人在躲避轨迹上障碍物时与临近轨迹其他障碍物发生碰撞的情况，具有较好的鲁棒性；Seder等［5］针对移动的障碍物环境，在动态窗口法的基础上，将障碍物的移动视作为所占据网格单元的移动，与机器人的运动单元轨迹进行碰撞预测，扩展了机器人在移动障碍物存在时的无碰撞运动能力。但是现有的DWA算法依然存在以下问题：①在障碍物较稠密区域，动态窗口法在穿越稠密障碍物时存在绕行于稠密障碍物区域外侧，造成总路程增加。②遇见“C”形障碍物组合时，会陷入评价函数失灵，需要通过边界跟随来逃逸，造成移动机器人运动轨迹不平滑的同时，安全性也无法得到保障。

综上，本文提出了基于改进型DWA的移动机器人避障路径规划。首先，基于本文提出的关键航迹点的概念，提取出A*全局规划路径轨迹中的关键航迹点。然后，以关键航迹点到待评价轨迹的距离作为依据，定义新的评价子函数，获得新型DWA评价函数。在实现局部最优避障的同时，加入全局规划的指导，从而实现了规避陷入“C”形障碍物组合以及绕行于稠密障碍物区外围的问题，降低了移动机器人运行总路程和迭代次数，同时提升了运动的安全性。

1 改进型DWA算法

1.1 传统DWA算法

在传统的动态窗口法中，在模拟机器人的移动轨迹前，需要建立机器人的运动模型。图1为典型的移动机器人运动学模型示意图。

v(t)和w(t)分别代表了移动机器人在世界坐标系中的线速度和角速度。在每个采样周期内，对机器人的移动轨迹做近似化处理，将每个采样周期内的运动路径看作是直线，则t+1时刻的移动机器人位置(x(t+1)，y(t+1))为

图1 典型移动机器人运动模型Fig.1 Typical motion model of mobile robot

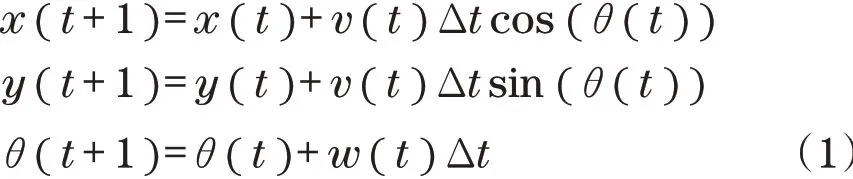
即移动机器人沿着方位角方向线性移动v(t)Δt，其方位角相对于世界坐标系移动w(t)Δt。

根据移动机器人的运动模型，在获取速度的基础上，就可以进行轨迹推算。因此，动态窗口法算法的两个核心分别是：①根据障碍物环境及机器人自身的机械特性等形成速度约束，生成动态窗口进行速度采样。②依据评价函数，对所采样的速度相应的预测轨迹进行评分，从而获取最优路径并执行。

速度采样时，移动机器人的速度主要受如下约束：

（1）移动机器人受自身最大、最小速度的限制，也是DWA算法求解速度的最大范围Vi：

（2）受移动机器人自身电机的影响，其增速降速提供的力矩有限，因此，在模拟机器人前向移动的周期内，存在动态窗口，即该窗口内的速度是机器人在自身机械特性影响下所能实现的实际速度Vj：

式中：vc为机器人当前的线速度；v˙a（v˙b）为机器人的最大加（减）线速度；wc为机器当前的角速度；w˙a（wb）为机器人的最大加（减）角速度。

（3）为了实现安全避障，不与占据一定空间的障碍物发生碰撞，在减速最大加速度条件下可得范围Vk，进一步缩小动态窗口范围：

式中：dist(v，w)为相应速度的预测轨迹上的障碍物距离最小值。

综上，根据机器人自身的机械特性和障碍物环境，可以定义动态窗口为

动态窗口中的采样轨迹如图2所示。运动轨迹主要是根据移动机器人每个线速度角速度的采样点以及前向仿真时间tsim生成的。

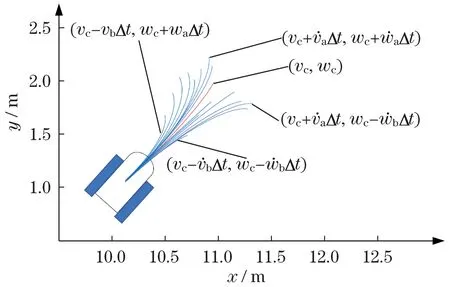
图2 动态窗口采样轨迹Fig.2 Dynamic window sampling trajectory

获取移动机器人运动轨迹以后，需要评价函数对各个路径进行评分，选取其中分值最高的作为综合最优路径并执行：

式中：heading(v，w)为偏转角评价子函数，该子函数的作用是评价在该模拟轨迹速度下的轨迹末端方向与目标点之间的角度差，其公式为180°-θ（θ越小，得分越高，其中，θ为所采样轨迹末端点朝向与机器人和目标点连线的夹角），该子函数主要作用是促进移动机器人在运动过程中其方位角不断朝向目标点；distance(v，w)为安全系数评价子函数，该子函数的作用是剔除掉有可能与障碍物发生碰撞或者接触的采样路径，实现移动机器人的安全避障，为避免该评价函数占比过大，对没有障碍物的采样路径进行评分时，安全系数评价子函数设定为常数；velocity(v，w)为速度评价子函数，该子函数的作用是在可以实现安全避障的采样轨迹中，选择出速度最快的路径，以尽快到达目标点。

1.2 改进型DWA算法

在传统DWA算法中，存在以下缺陷：

（1）由于缺少全局规划，移动机器人一旦面对由几个距离相近的障碍物构成的“C”形障碍组合时会出现评价函数失灵，无法进行正确的路径选择，需要执行边界跟随处理。但是，一方面该处理方法会导致机器人与障碍物距离过近而无法保证安全性；另一方面因边界选取具有一定随机性，不受评价函数控制，往往会增加移动机器人的总路程。

（2）通过稠密障碍物区域时，传统算法中的移动机器人往往会选择从稠密障碍物区域的外围绕行，增加移动机器人运动的总路程。

针对传统DWA算法中的以上缺陷，提出基于改进型DWA的移动机器人避障路径规划。

1.2.1 转点评价子函数keypoint(v，w)

在移动机器人基于DWA算法执行动态避障的过程中，如果能够在关键转折点处调整方向，提前绕开“C”形障碍物组合，通过稠密障碍物区，便可以实现总路程的减少和安全性提升。因此，本文在传统DWA算法的3个评价子函数基础上，增加了参考全局路径规划算法关键航迹点位置的新型评价子函数——转点评价子函数。该子函数的作用是帮助移动机器人提前绕开“C”形障碍物组合，并提升稠密障碍区的通过性，在规避多余绕行的同时提升机器人运动的安全性。

在障碍物为静止状态的环境下，A*算法是规划移动机器人的全局最短路径的最有效算法。该算法的核心是代价函数为

式中：f(s)为从出发点到当前点再到终点的代价估计值；g(s)为从出发点到当前点的实际距离；h(s)为启发式函数，指当前点到终点的估计值。当h(s)=0时，A*算法便等同于Dijikstra算法。该算法基于Dijikstra算法，结合启发式函数BFS，在搜索最短路径的同时，通过启发式搜索来提升效率。

但是A*算法搜索出的最短路径中的规划节点通常较多，难以满足机器人移动的稳定性和运动轨迹平滑性的要求，无法直接作为DWA算法的全局路径规划指导。因此，本文提出了关键航迹点集合Mp的概念，具体定义如下：

（1）针对A*算法规划的全局路径中的节点，如果出现多个航迹点相对于世界坐标系处于同一条水平或者竖直直线上，则认为同一条线上的末端节点为关键航迹点并提取。

（2）针对A*算法规划的全局路径中的节点，如果出现多个航迹点处于同一条直线上，但是相对于世界坐标系不处于同一条水平或者竖直直线上，则认为同一条线上的首个节点为关键航迹点并提取。

（3）针对A*算法规划的全局路径中的节点，则认为临近起点以及终点的1个节点为关键航迹点并提取。

在遍历所有A*算法规划的全局路径中节点后，提取出其中的关键航迹点，计算动态窗口中各个采样速度的前向仿真轨迹与关键航迹点的最小距离，其结果作为转点评价子函数keypoint(v，w)对各个轨迹评分的依据。由此，得到新型DWA评价函数为

同时，需要对各个评价子函数进行归一化处理。以安全系数评价子函数为例，各个采样轨迹中，避障的安全距离是离散化的，比如有的轨迹就不会出现障碍物而常数化处理。这样就会导致安全系数评价子函数不连续并且子函数中某项可能占据比重过大，造成轨迹不平滑。因此，需要对安全系数评价子函数进行如下归一化处理：

对各个评价子函数进行归一化处理后，最终得到相对平滑的避障路径轨迹。

1.2.2 改进型DWA算法流程步骤

综合上述内容，改进型DWA算法流程具体步骤如下：

步骤1根据传感器获取地图中的移动机器人以及障碍物位置并构建模拟地图；

步骤2初始化A*算法并开始搜索，根据选取的计算点，计算下一个航迹点的f(s)、g(s)、h(s)，然后更新搜索航迹点，直至到达目标点，获取所有航迹点；

步骤3提取出A*路径中的关键航迹点并添加进模拟地图中；

步骤4初始化改进型DWA算法并设置参数，包括最大线速度、最小线速度、最大角速度、最小角速度、线加速度、角加速度、线速度分辨率、角速度分辨率、时间分辨率、轨迹预测时间、障碍物半径以及各个评价子函数的权值；

步骤5根据移动机器人机械特性和障碍物环境更新速度范围，确定由所有可行速度组成的动态窗口；

步骤6根据移动机器人的运动模型，生成动态窗口中的每个采样点前向仿真时间tsim内机器人的运动轨迹；

步骤7根据改进型DWA算法评价函数给各个采样轨迹打分，并对4个子函数进行归一化处理，评分最高的最优速度组合作为t+1时刻移动机器人的运动速度；

步骤8执行最优速度，并检查是否已经到达路径的目标点，若不是，则返回步骤5，若是，输出结果，获得最优路径。

2 仿真验证及结果分析

为了验证基于改进型DWA的移动机器人避障路径规划可以规避“C”形障碍物组合，提高稠密障碍区的通过性，实现安全性提升和路径优化，在相同的障碍物环境地图内进行传统DWA和改进型DWA的对比实验。

2.1 基本参数

对比实验中涉及的基本参数包括移动机器人的机械特性、DWA算法的基本参数、评价函数的参数（转点评价子函数权值参数为改进型DWA算法特有），实验的具体参数如表1～表3所示。

表1 移动机器人机械特性Tab.1 Mechanical characteristics of mobile robot

表2 DWA算法的基本参数Tab.2 Basic parameters of DWA

表3 评价函数参数Tab.3 Parameters of evaluation function

在本实验中，当移动机器人到达目标点半径0.5 m范围内，便视为到达目标点。

2.2 对比仿真结果及分析

图3 是本次实验中构建的模拟地图。各个障碍物以黑点为圆心，轮廓为半径0.3 m的圆表示。在模拟地图中，坐标为（3，3）的小圆代表移动机器人出发的起始点，坐标为（13，13）的小圆代表移动机器人的目标点。

图3 模拟地图Fig.3 Simulation map

图4 为基于传统DWA算法的移动机器人避障路径规划。在该路径轨迹中，移动机器人在通过坐标为（4，6）、（5，5）、（5，6）3个障碍物构成的“C”形障碍物组合时，评价函数失灵，出现了边界跟随的情况，降低了机器人运动的安全性和稳定性。在通过坐标为（8，9）、（9，8）、（10，8）、（11，8）等障碍物组成的稠密障碍区时，移动机器人选择了绕过该区域，增加了移动机器人的运动总路程。该路径迭代次数为503次，运行时间为58.7 s，总路程为19.2 m。

图4 基于传统DWA算法规划的路径轨迹Fig.4 Path planning based on traditional DWA algorithm

图5 中的“+”图标是通过A*算法搜索出的全局最短路径的航迹点。根据关键航迹点的定义对该最短路径中所有的航迹点进行筛选。筛选完成后的关键航迹点如图6所示。

图5 全局最短路径中的节点Fig.5 Nodes in the global shortest path

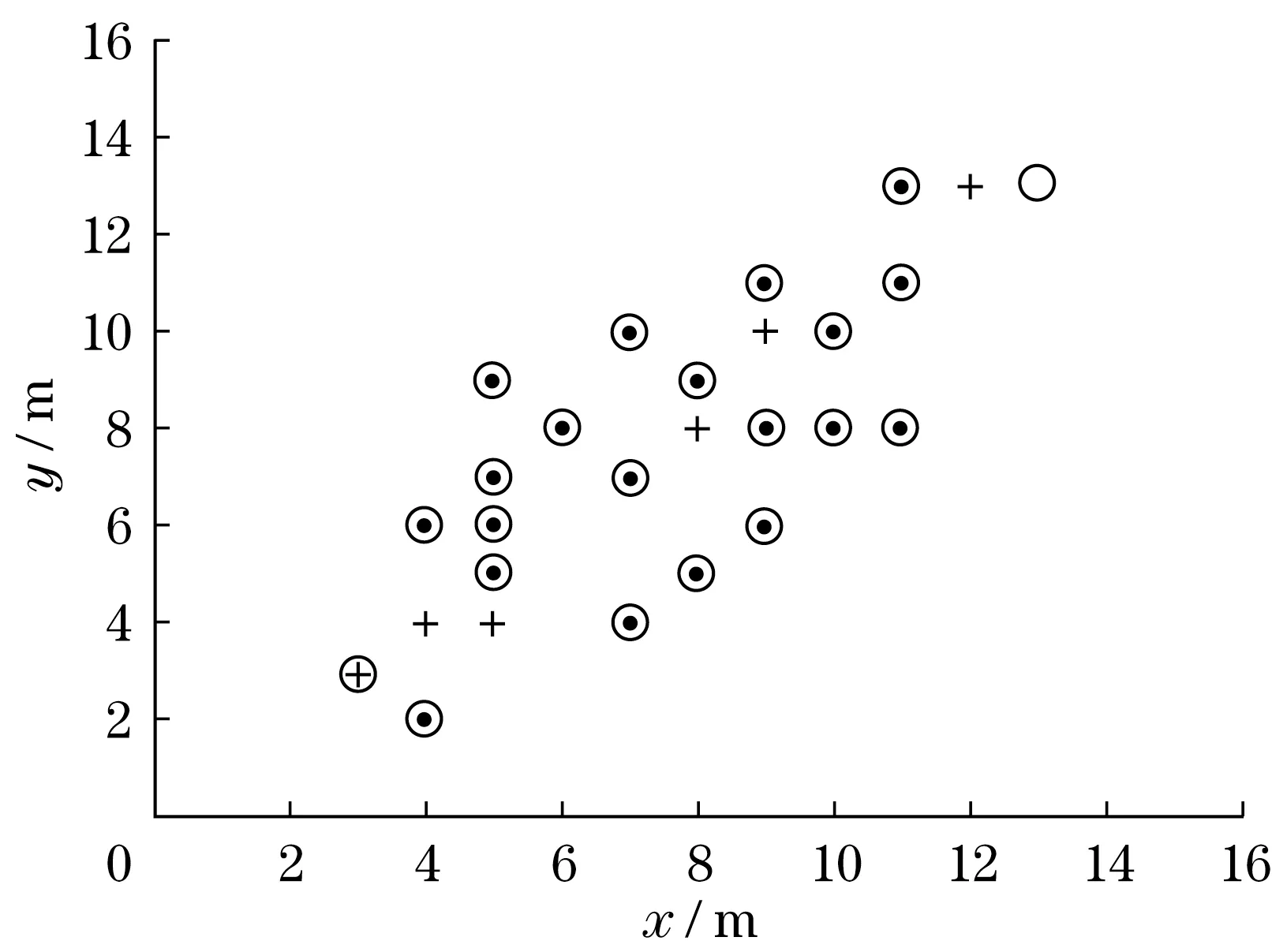
图6 全局最短路径中的关键航迹点Fig.6 Critical track points in the global shortest path

图7 是基于改进型DWA的移动机器人避障路径规划生成的轨迹。可以明显看到在坐标为（4，4）、（8，8）、（9，10）等关键航迹点处，在转点评价子函数的作用下，移动机器人分别实现了提前规避“C”形障碍物组合和避免绕行稠密障碍物区。该路径的迭代次数为447次，运行时间为51.5 s，总路程为16.3 m。

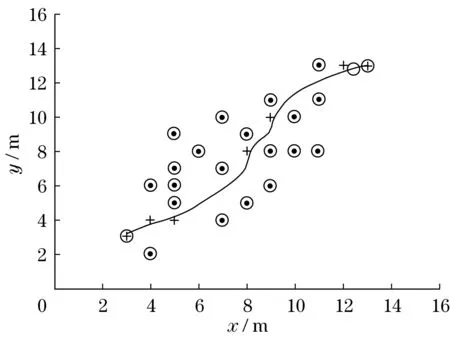
图7 基于改进型DWA算法规划的路径轨迹Fig.7 Path planning based on improved DWA algorithm

对比改进前后路径轨迹，改进型DWA算法实现了提前规避“C”形障碍物组合，并提高了稠密障碍物区的通过性。将改进前后的运行时间、迭代步数、总路程填入表4中，以便进行定量比较。

表4 算法改进后数据对比Tab.4 Data comparison after algorithm improvement

3 结语

在传统DWA算法中，移动机器人穿越稠密障碍物区域时会绕行于稠密障碍物区域外侧，造成总路程增加，以及遇见“C”形障碍物组合时，会陷入评价函数失灵，需要通过边界跟随来逃逸等问题，以致于在机器人移动总路程增加的同时，安全性也无法得到保障。针对以上问题，本文提出基于改进型DWA的移动机器人避障路径规划，定义了关键航迹点的概念，根据定义提取出A*全局规划路径节点中的关键航迹点。根据关键航迹点到待评价轨迹的距离，定义新的评价子函数，获得新型DWA评价函数。仿真实验结果表明，新型评价函数解决了以上问题的同时，整体性提升了移动机器人的运动效率。未来的研究方向是处理动态障碍物环境中移动机器人的避障路径规划优化。