钻头圆锥钻齿切削岩石数值模拟以及一种新的解析估算模型

刘宏亮，尹 莉，付 玲，王霄腾

（中联重科股份有限公司建设机械关键技术国家重点实验室，湖南长沙410013）

提高旋挖钻入岩工作效率是目前旋挖钻优化设计的主要目标。针对目前钻进硬质岩层效率较低的问题，需要改进和优化钻进切削方案。钻齿切削岩石过程中有不同的切削参数，如切削厚度、切削速度、钻齿的切削角度等，钻齿切削岩石机理研究能计算钻齿切削过程中的切削作用力以及岩石破碎响应。准确的切削数值仿真结果，能提升设计人员对岩石破碎机理的认知，并能为旋挖钻优化钻进工作效率提供有用的数据参考以及技术支持。

圆锥形钻齿是较常见的钻齿形状，旋挖钻用于硬质岩石的筒钻往往配备圆锥形钻齿。目前钻齿切削岩石响应研究集中在两个方面：一是数值模拟钻齿切削岩石过程；二是解析经验公式估算钻齿在切削过程中的作用力。数值模拟计算基于非线性有限元计算，运用塑性损伤模型模拟仿真岩石的破碎过程。Menezes等［1］运用显式LS-DYNA有限元计算了岩石破碎过程；贾彦杰等［2］运用Drucker-Prager模型分析了扩孔器切削齿切削岩石作用力；欧阳义平等［3］运用光滑粒子算法（SPH）分析了圆锥钻齿的切削响应，并将计算结果用于拟合计算切削作用力的经验公式。除了数值仿真计算，力学解析求解能快速估算钻齿切削作用力大小。Evans［4］推算了圆锥齿切削岩石切削作用力的解析求解公式。Goktan［5］在此基础上考虑岩石抗拉强度、切削深度等因素完善了解析估算模型，并且提出了一种半经验计算方法［6］。上述解析估算方法在有些情况下与试验测试值相差较大。欧阳义平等［7］结合试验数据拟合出估算岩石切削作用力的经验公式，但一定程度上缺乏力学理论支撑。

上述钻齿切削研究提供了钻齿切削岩石破碎响应的基本方法，本文将基于Drucker-Prager塑性模型，运用非线性有限元计算系统地分析切削厚度、切削角度与钻进切削作用力的关系，并与试验测试值进行对比验证数值计算的准确度。另外，根据岩石内聚力以及抗压强度，结合岩石破碎的力学分析，本文给出一种新的三维圆锥钻齿切削岩石切削力计算的解析方法，并与试验测试结果对比验证模型的计算精度，从而完善现有切削作用力的解析估算方法。本文提出的圆锥钻齿切削岩石的数值方法以及解析估算方法，在一定程度上为旋挖钻钻头的结构优化设计提供技术支持以及理论辅助。

1 数值模拟方法

1.1 几何模型

常见的圆锥形钻齿切削岩石示意图如图1所示（实际钻齿形状较复杂会有一些差异，这里简化为圆锥形）。主要的钻进工作参数有切削厚度、切削速度以及切削角度。本文将切削角度分为切削前角、钻齿半锥顶角以及切削角，为了简化计算以及匹配相关试验测试，将实际旋挖钻旋转切削简化为横向直线切削，并将钻头钻齿和岩石的几何模型简化，如图1所示。

图1 圆锥形钻齿岩石切削示意图及切削数值模拟的几何模型Fig.1 Schematic for rock cutting with the conical pick and the geometry for numerical simulation

1.2 材料本构模型

钻齿设定为刚体，岩石的材料特性需考虑非线性弹塑性，常用的Drucker-Prager模型被研究认为能很好地模拟岩土等材料的塑性变形特征，其屈服函数为［8］

式中：I1为应力张量第1不变量；J2为应力张量第2不变量。

准则参数α、k定义为［8］

式中：θσ为应力Lode角；φ为内摩擦角；c内聚力。

根据应力Lode角的取值，可以将塑性硬化分为压缩硬化、拉伸硬化和剪切硬化。

相关力学参数可以通过相应试验进行测试，包括抗拉、抗压强度，内聚力以及内摩擦角等。文献［7］对砂岩进行了圆锥钻齿切削试验并测试了砂岩的各项材料特性参数。经测试，砂岩的材料特性参数如表1所示。

表1 砂岩材料特性参数［7］Tab.1 Material properties for sandstone［7］

根据线性剪切标准，可以修正Drucker-Prager模型，其屈服函数和塑性势面函数可定义为［9-10］

式中：t为偏应力；p为等效压应力；β为线性屈服面在p-t应力空间上的倾角；Ψ为剪胀角；q为Mises等效应力；r为偏应力第3不变量；K为三轴拉伸强度与三轴压缩强度之比；d为屈服面在p-t应力空间t轴上的截距，跟硬化准则有关，对应3种硬化方式——压缩硬化、拉伸硬化和剪切硬化［9］。

根据受压屈服应力σc［9］

考虑到试验数据只提供了抗压和抗拉两种强度，因此只模拟计算上述两种计算强度。另外，修正的Drucker-Prager模型考虑了岩石在剪切变形下的体积膨胀效应并定义了剪胀角Ψ，本文后续计算中考虑了不同剪胀角对计算的影响。考虑到钻齿切削岩石过程中，岩石会发生损伤破碎从而产生材料失效，采用相关失效准则［11］模拟岩石破碎。

1.3 有限元相关设置

采用显式动态分析模拟钻齿切削岩石过程，钻头为刚体。计算边界条件设定为：岩石块的地面设定为刚性约束。模拟钻齿横向切削岩石破碎，钻齿横向位移设定为40 mm，切削速度为2 m/s。文献［7］没有给出试验过程中具体的切削速度值，但根据本文的数值模拟计算可知当切削速度小于2 m/s时，不同的切削速度不会引起切削作用力较大的变动，具体在第4节会详细介绍。同时，钻齿的表面和岩石表面定义面接触。

2 一种新的圆锥钻齿切削作用力解析计算模型

除了数值模拟外，可以根据岩石抗压强度和内聚力，从钻齿岩石切削过程中的受力分析估算钻齿切削岩石作用力的大小。切削作用力的解析计算能辅助验证数值模拟的准确性，并可以通过匹配试验数据完善解析计算公式，从而可以通过解析计算直接快速获得切削作用力大小。如图2所示，在圆锥钻齿横向向左切削过程中，会在前方产生一个类似于四面体形状的破碎岩石块（图2右下角），其中AB为切屑剪切破坏线，其与水平面的夹角称为剪切角γ。

图2 钻齿切削过程中的受力分析Fig.2 Force analysis for rock cutting with the conical pick

破碎岩石块在切削破碎过程中，受到右端面钻齿的切削作用力以及与岩体接触的两个侧面的剪切力作用，如图2左下力学分析示意图所示。右端面受到钻齿的切削作用力可以分解为端面上的FN以及Ff，

式中：σc为岩石的抗压强度；A为岩石块右端面面积。

考虑到岩石与钻齿接触右端面为圆锥面，为了简化计算将其等效为在圆锥中心面上的投影三角形，因此其面积可以计算为

Ff未知，需求解。岩石块与岩石整体接触的两个侧面受到剪切作用力Fc以及法向作用力FcN（见图2）。其中，剪切作用力与岩石内聚力c以及内摩擦角φ有关，根据相关计算最终可得（计算过程比较繁琐，这里略去中间计算步骤）

式中：As为侧面面积（为了简化计算将其侧面积等效为中心面投影三角形ABC'的面积，后续的力学平衡计算也在此中心面上计算）为

钻齿在切削过程中的作用力与岩石块右端面作用力方向相反大小相等，根据岩石的抗压强度，FN已知，需要求解Ff的大小。考虑到岩石块受力平衡，左端两个侧面的作用力与右端受力大小相等方向相反，因此将上述作用力进行正交分解，如图2左下图所示。受力平衡方程可计算为

两个方程两个未知数，根据式（11）可求得

联合上述方程可求得

圆锥钻齿切削岩石作用力幅值可以计算为

由FN、Fc的计算方程式可知，钻齿切削作用力的大小与岩石抗压强度、岩石内聚力、内摩擦角、各个切削角度、切削厚度有关。

3 计算结果

3.1 切削数值计算结果与试验测试以及解析估算值的对比

根据文献［7］的描述，钻齿切削试验方案包括不同切削角以及切削厚度的设定。本文将对照试验测试方案，根据试验测试所得对应的岩石材料特性参数分别进行了数值仿真模拟以及解析估算。解析估算按式（14）进行计算，对于剪切角γ的设定，切削厚度对剪切角有一定的影响，通常情况下切削厚度越小剪切角也越小。因此，对应不同的切削厚度设定不同的剪切角：切削厚度5 mm对应剪切角30°，切削厚度10 mm对应剪切角40°，切削厚度15 mm对应剪切角60°。另外，因为岩石材料特性（见表1）未给出相应岩石的剪胀角，在数值模拟计算中测试5种剪胀角（0°～20°）的计算并与试验测试结果对比。同时，对应岩石的抗拉强度和抗压强度分别计算抗拉、抗压条件下Drucker-Prager模型的数值模拟计算结果。数值计算值、解析估算值与实验测试数据的对比如表2所示。考虑到数值计算采用动态显示分析，计算所得钻齿切削作用力（接触压力作用反力）在切削过程中有一定的波动，这里采用峰值进行对比（因为试验未给出摩擦系数，这里暂时不计入摩擦力，下一节具体讨论摩擦力的影响）。半锥顶角为20°的情况根据图1所示的几何尺寸作相应调整（图1尺寸考虑整数设定，对应半锥顶角为29.7°，这里近似为30°）。

从表2可知，切削厚度对钻齿切削作用力影响较大，钻进过程的切削角度对切削作用力也有一定的影响。与试验测试值对比可知，根据式（14）估算的钻进切削力大小与试验值有一定的匹配度，解析估算值与试验测试值误差的绝对值在30%以内。数值计算结果则出现两种不同情况，以抗拉强度为计算准则的仿真结果与试验测试相差较大，而以受压强度为计算准则的数值仿真结果能一定程度上匹配实验测试值，尤其是在切削厚度为10、15 mm时，数值模拟结果与实验测试值相差不大。因此，以受压强度为计算准则的Drucker-Prager模型能较准确地模拟切削岩石过程中钻齿的受力情况。另外，剪胀角对计算结果的影响很小，增加剪胀角能一定程度地增加切削作用力，但增加幅度很小。

3.2 钻齿表面与岩石接触摩擦力的影响

因文献［7］并没有给出试验过程中摩擦系数的大小，表2列出的数值计算值没有计入钻齿表面与岩石接触面的摩擦力。这里，通过假定一个常用的摩擦系数考察接触面摩擦力对总的钻进作用力的影响，摩擦系数选取为0.2计算过程中，岩石材料特性如表1所示，切削厚度、钻齿半锥顶角和切削前角设定如表2所示（共4个组合），剪胀角设定为10°，并采用抗压强度进行计算。所得钻齿切削作用力与不计入摩擦力的计算结果对比如表3所示。由计算结果可知，在所假定的摩擦系数下，钻齿表面与岩石接触面的摩擦力对总的切削作用力有一定的影响，因此，如能在试验中获得准确的摩擦系数值能增加数值模型的计算精度。

表2 数值计算值、解析估算值与实验测试数据的对比汇总Tab.2 Summary and comparison for numerical results，analytical results and experimental data

表3 钻齿与岩石接触面摩擦力对数值计算结果的影响分析Tab.3 The analysis for the influence of the friction from the contact surface between the pick and rock on the cutting force

4.3 不同厚度不同切削速度的数值模拟

在上述的数值模拟以及解析估算过程中，暂未考虑切削速度的影响。数值模拟计算采用的切削速度为2 m/s，解析估算则没有考虑切削速度的影响。为了进一步分析切削速度对钻进作用力的影响，运用上述数值模型模拟计算不同切削厚度对应不同切削速度下的岩石切削破碎响应。共测试3种切削厚度，分别为5、10和15 mm；同时测试4种切削速度，分别为0.1、0.5、1和2 m/s。岩石材料特性如表1所示，钻齿半锥顶角设定为30°，切削前角为20°，剪胀角设定为10°并采用抗压强度准则进行计算，所得的钻齿切削作用力如表4所示。从计算结果可知（未计入摩擦力），在切削速度小于2 m/s时，切削速度对钻齿切削作用力的影响较小。具体地，当切削厚度为5 mm时，切削作用力随切削速度的改变而产生一定的波动但幅度不大；当切削厚度为10 mm时，切削作用力随着切削速度的增大而略微增加；当切削厚度为15 mm时，切削作用力随切削速度增大而增加，但增加幅度不大。因此，在切削速度小于2 m/s时，钻齿切削岩石的速度对钻齿切削过程中的切削作用力的影响较小。

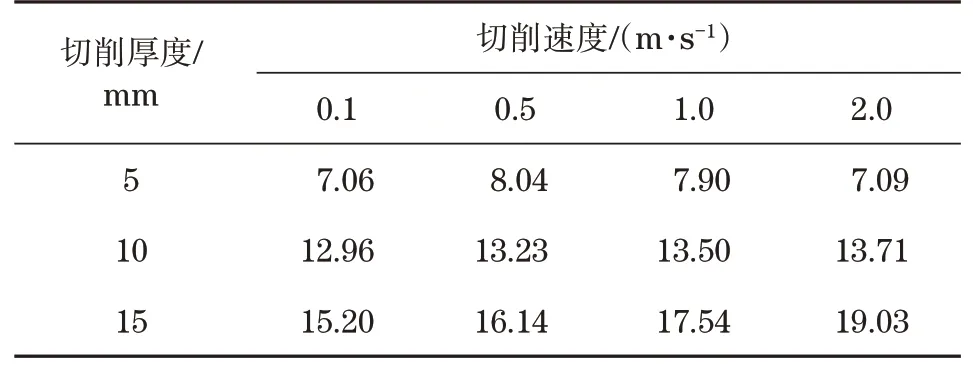
表4 不同切削厚度不同切削速度下的数值模拟结果Tab.4 Numerical simulation results with different thicknesses and cutting speeds kN

5 结论

为了深入分析旋挖钻钻头圆锥形钻齿切削岩石破碎机理，本文基于Drucker-Prager塑性损伤模型对圆锥钻齿切削岩石进行数值仿真模拟。同时，根据岩石切削破坏过程中的受力分析，以及岩石抗压强度、内聚力、内摩擦角的大小，推导了一种新的圆锥钻齿切削作用力解析求解计算公式，可以得到如下结论：

（1）本文对某砂岩的数值模拟，以抗压强度准则进行计算，能更好地匹配实验测试数据。

（2）岩石剪胀角对数值仿真计算结果的影响较小。

（3）本文根据岩石抗压强度、内聚力以及内摩擦角进行岩石受力分析，所建立的解析估算模型被验证有一定的计算精度，可考虑用来估算圆锥钻齿切削岩石作用力的大小。

（4）在小于2 m/s的切削速度范围内，切削速度的变化对切削作用力的影响较小。