基于系统动力学的地铁客流防疫调控仿真分析

胡明伟，李微微，陈湘生

1) 深圳大学土木与交通工程学院，广东深圳 518060；2)深圳大学滨海城市韧性基础设施教育部重点实验室，广东深圳 518060；3)深圳大学未来地下城市研究院，广东深圳 518060

随着新型冠状病毒肺炎(corona virus disease 2019，COVID-19)后疫情时代的复工复产，地铁的客流量也逐步增加，境外输入病例时有出现，且存在一定数量的无症状患者[1]，因此，如何在保证居民正常出行需求下，尽可能降低感染风险成为地铁运营亟待解决的问题之一．同时，采取主动措施调控车站客流，对确保乘客安全以及提升运输效率具有重要作用．

目前，中国已有研究利用微观仿真建模方法分析地铁站内的客流问题．胡明伟等[2-3]采用微观仿真模型评估地铁站的客流组织和管理．JI等[4-5]通过观测分析地铁车站内客流，提出一种改进的社会力模型和元胞自动机模型．TRIVEDI等[6]基于智能体建模方法分析并计算地铁站乘客从候车区到上车的总时间．相比微观仿真模型，系统动力学方法能对系统进行全局分析，具有建模速度快、对不同方案的比选工作量更小的优势．陈春安等[7-9]利用系统动力学模型对地铁车站客流进行推演仿真分析，结果表明该模型方法能够预测分析客流．

已有研究表明[10-12]，目前地铁的相关调控策略多是基于乘客安全、通行效率以及地铁的承载能力制定，突发事件下策略选择需考虑的影响指标有待改进．如新冠病毒疫情影响下，根据《中国-世界卫生组织新型冠状病毒肺炎(COVID-19)联合考察报告》中的相关研究[13]，新冠肺炎的潜伏期一般为1～14 d，平均潜伏期为5～6 d，有可能存在无症状感染者乘坐地铁，因此，疫情防控期间地铁运营方在制定调控策略时还需考虑措施对乘客感染概率的影响．新型冠状病毒通过飞沫和空气传播时受到诸多因素的影响，如传播环境、病原体数量与种类、及飞沫在不同室内环境的蒸发和散布特性等，由于其中部分影响因素的参数无法精确计算，且有些影响因素的研究起步较晚，因此，较难从机理上准确预测呼吸道传染病的感染概率．目前，呼吸道传染病的预测模型多基于统计学预测疾病的感染风险和传播概率，如SI、SIS、SIR、SIRS及SEIR模型等[14-15]．张毅等[16]通过研究传染病学统计预测模型，提出交通出行易感度概念，并分别计算了不同交通工具的易感度．

本研究考虑新冠病毒的传播特点，运用系统动力学理论，建立一种地铁站客流组织模型，并利用该模型分析疫情影响下采用不同客流调控方案对地铁站出行易感度的影响，以期为地铁站运营管理方采取科学防疫措施和评价提供参考．

1 理论概述

1.1 研究框架

运用系统动力学模型进行客流调控仿真和评价的研究框架如图1．研究利用系统动力学，客流组织分析以及考虑疫情的调控措施等手段搭建地铁站客流组织系统动力学模型，依据基础数据仿真多种调控措施，利用仿真结果分析其对地铁站客流动态变化及易感度评价参数的影响．

图1 研究框架Fig.1 Research framework

1.2 考虑疫情的客流调控措施

考虑COVID-19疫情对轨道交通的影响，为了降低站内传染风险，保证乘客及工作人员的安全，以及站内的服务水平和质量，需采取合理的客流调控措施．制定疫情下调控措施可以从降低站内人员密度，增加人员间距以及减少站内驻留时间等方面考虑；而传统的调控措施主要考虑通行效率，以及当站内承载能力超过最大负荷时，避免由于拥堵而引发安全隐患，两者可能会存在矛盾，因此，调控措施需综合考虑制定．

地铁站客流组织可大致分为进站、出站及换乘过程，具体流程如图2．本研究仿真选择4种常用调控措施：限制进站客流量、控制服务设施数量、延长站厅走行流线以及增加地铁发车频次．

图2 地铁站客流组织Fig.2 Passenger flow organization of metro station

限制进站客流量包括设定站外导流栏杆与限制入站客流量等．疫情期间，北京地铁曾采用预约进站策略，即限制高峰时段进站人数的预约名额，乘客可以通过手机预约进站时段，预约成功后，由站内专门的预约通道快速进站乘车，从而减少无效的站外排队时间，降低站外人员聚集风险，同时也降低了地铁客流密度，控制地铁车厢的满载率．

控制服务设施数量包括调整服务设施(如闸机、 安检设备及楼扶梯等)的布局、数量和服务速率．

延长站厅走行流线包括设置导流栏杆调整站内客流线等．疫情期间，通过在排队地面粘贴1 m排队间隔线等方式控制人员间距．

增加地铁发车频次包括限制客流上车人数，增加地铁列车频次等．限制上车人数是为了降低列车载客率，增加地铁列车可以有效减少站台滞留乘客，减少对乘客出行效率的影响．

1.3 考虑疫情的调控措施评价参数

依据文献[10-12]，在保障运营管理高效和乘客出行安全的前提下，制定客流调控方案需考虑平均等待时间、平均停留时间、站厅承载客流、站台承载客流及上车人数等参数．但考虑到疫情对地铁运营的影响，在制定合理运营措施时，还应分析不同措施对传染控制的影响．

WELLS[17]提出quanta概念，从个人角度确定空气传染病的感染概率，1个quanta即1个人达到致病量的最少病原体数量，具有统计意义概念．若假设飞沫核均匀散布于整个空间，可计得一个人在空气中呼吸所得的quanta值，通过计算有效接触率，从而计算感染概率．

由于Wells理论没有考虑平均感染概率的差异，当quanta值很高时，计算出的感染概率可能超过1，因此，RILEY等[18]提出基于Wells假设的Wells-Riley模型，为

(1)

其中，P为感染概率；I为感染人数；p为呼吸通风量(单位：m3/h)；q为一个感染者的quanta产生率(单位：quanta/h)；t为暴露时间(单位：h)；Q为房间通风量(单位：m3/h)．

FENNELLY等[19]考虑口罩等的作用后，提出改进的Wells-Riley模型，为

(2)

其中，θ为口罩的渗透系数， 0≤θ≤1．

张毅等[16]依据传染病学提出交通出行易感度概念，即乘客通过乘坐交通载运工具接触到陌生个体中的感染者且被传染的概率，并利用改进Wells-Riley模型对不同交通工具的易感度进行定量计算，综合考虑风险程度的决定因素及进行参数化后，得到交通出行易感度Pi为

(3)

其中，Nai为第i种交通运输工具的实际载客人数；Nbi为第i种交通运输工具的标准额定载客人数；Vi为第i种交通运输工具的体积(单位：m3)；ni为第i种交通运输工具每小时的通风次数(单位：次/h)；αi为交通运输工具消毒措施带来的保护系数， 0≤αi≤1． 本研究借鉴该交通出行易感度概念分析不同调控措施下站台层和站厅层各区域的客流易感度变化．

2 模型构建

本研究利用AnyLogic仿真平台构建系统动力学(system dynamic, SD)模型．其中，系统动力学模块建模构成要素包括存量、流量、辅助变量及常量．通过分析地铁客流组织系统的因果关系，利用构成要素建立系统的存量和流量图来反映系统中的辅助变量和状态变量关系，并通过量化存量和流量图的各因素关系完成客流组织仿真模拟．

2.1 基本SD模型

地铁站客流SD模型的仿真区域分为站厅非付费区、站厅付费区及站台层．通过分析影响车站上述3个区域客流量的相关变量，构建地铁车站各处的因果关系图，结果请扫描论文末页右下角二维码见图S1．

地铁内部客流按照乘坐目的可以分为进站客流、出站客流及换乘客流，换乘方式包括同站台换乘、站厅换乘、通道换乘及出站换乘等，不同换乘方式对各个区域客流的影响程度不同．依据因果关系及地铁客流组织分析，并对影响因素与换乘客流进行合理简化后，建立客流系统动力学模型，请扫描论文末页右下角二维码见图S2．模型各变量参数定义请扫描论文末页右下角二维码见表S1．

依据车站内客流动态变化的逻辑关系与数学关系，建立系统动力学方程．

1)各存量的计算方式为累计流入量减去累计流出量，为

(4)

其中，Qi为地铁站内i处t时刻总流量；qiin(t)为i处t时刻的流入流率；qiout(t)为i处t时刻的流出流率．

2)各服务设施，如购票、安检或闸机处客流流出速率为

qi(t)=min (Ci×ni，Fi(t-1) )×vi/Li

(i=2,3,4,5,6,9,11,13)

(5)

其中，qi(t)为i处t时刻的流出速率；ni为i处服务设备数量；Ci为该服务设备单个服务能力；vi为i通道内客流平均速度；Li为i通道长度．

3)辅助存量的客流流出速率为

Fi(t)=min(Ci×ni，Fi(t-1))

(i=1,2)

(6)

其中，Fi(t)为i处t时刻的流出速率．

此外，q1数值上等于乘客的到达率．数值的单位按照人/s设置．

2.2 考虑疫情的调控模型

疫情发生后，全国多个地铁公司均采取相应措施以应对地铁高峰及疫情防控，如深圳地铁于2020-03-05发布采用“一站一方案”模式的倡议，对出入口、站厅及站台3级进行客流管控措施；北京地铁于2020-03-06起试行推出 “预约进站”，即通过预约进站减少站外排队时间，降低地铁客流密度，从而控制地铁车厢的满载率，保障乘客出行安全，并于2020-03-31对4条地铁线路使用超常列车运行(即增加车辆投放)图来提高运力．评价不同调控措施效果往往需要进行实地评估或仿真计算，考虑到实地调查具有一定局限性和难度，本研究通过调整系统动力学模型的参数，仿真限制进站客流量、控制服务设施数量、延长站厅走行流线以及增加地铁发车频次4种客流调控措施，得到实时站点区域的人流数据，并计算感染概率，以期验证使用模型分析地铁站客流控制策略对易感度影响的可行性．在系统动力学模型中增加进站闸机数、出站闸机数、延长距离及修改上下车触发等参数，仿真模拟4种调控措施．建立模型如图3．

2.3 考虑疫情的感染概率模型

2.3.1 易感度计算模型

考虑到地铁站厅和站台公共区域的室内通风来源复杂，站厅出入口和站台层屏蔽门开关带来的隧道风均会影响公共区域的新风量．公共区域的人员流动与交通工具固定的额定载客人数定义亦不同．因此，改进交通出行易感度计算公式为

(7)

其中，Pi为健康者被感染的概率；Fai为第i区域的实际客流人数；Fbi为第i区域承载的最大客流人数；Ii为感染者人数；p为单一乘客的呼吸量(单位：m3/h)；Qi为第i区域单一乘客的通风量(单位：m3/h)；ti为第i区域的暴露接触时间(单位：h)；αi为第i区域消毒措施带来的保护系数， 0≤αi≤1；θi为第i区域乘客佩戴口罩的渗透系数, 0≤θi≤1．

图3 仿真调控措施的系统流图Fig.3 System flow diagram of modeling control measures

2.3.2 参数设置

1)人均通风量Qi． 《地铁设计规范》GB 50157—2013[20]规定，闭式运行时的地铁站内新鲜空气量不应少于12.6 m3/(h·人)，且系统新风量不应少于总送风量的10%．文献[21-22]指出对于车站公共区域的空调最小新风量标准一般取以下3者中的最大值：高峰期人员所需新风量(12.6 m3/(h·人))、系统总送风量的10%、以及屏蔽门漏风量和渗透风量之和．因此，本研究参考选择Qi=12.6 m3/(h·人)．

2)quanta产生率q． 由于不同病因、不同感染者所产生的quanta值均不同，目前暂无COVID-19疫情的quanta准确取值．张毅等[16]综合肺结核、麻疹、甲型H1N1流感及重症急性呼吸综合症(severe acute respiratory syndrome, SARS)的quanta产生率，估算COVID-19的q为100～122 quanta/h，考虑到公共区域人员流动性较大，本研究取q=122 quanta/h．

3)承载的最大客流人数Fbi． 常用的承载最大客流人数定义为能稳定运行的车站所能承载的最大乘客数．而站台承载能力可由设计有效面积(有效长度和宽度)和旅客最大安全密度决定[23]．文献[24]指出在实际运营过程中，通常采取经验估计，即当站内关键节点行人密度达到6人/m2时，需要采取相应措施．由于本研究主要计算满足区域最大乘客的新风量，所以Fbi按照站厅和站台层有效面积及人流密度0.5 m2/人计算．

4)防控措施的定量化参数． 防控措施主要体现在乘客是否佩戴好口罩以及站内的消毒效果，口罩渗透系数θi参考文献[16]取统计值0.2%．消毒指标保护系数αi取0.7．

3 案例分析

3.1 SD模型数据输入

因地铁站各区域客流组织状态特性不一，不同站厅的建筑与客流存在较大差别，本研究选择深圳地铁12号线在建的南山站为例，应用模型仿真分析无换乘客流影响情况下的客流调控．模型的乘客参数(如客流量及走行速率)、设备参数(如安检服务能力、 闸机服务能力及楼扶梯通行能力)取值参考初步设计图纸说明文件、其他站点相关文献及《地铁设计规范》GB 50157—2013[20]．

南山站12号线站厅层被桂庙路下穿隧道分割成左右两个端厅，站台为侧式车站，因此，车站模型分别取站厅西侧端厅和站台层的右线站台公共区数据进行仿真．依据实地调研，行人的步行速度为1.3～1.5 m/s．模型具体参数及其取值如表1.

表1 系统动力学模型参数设置

3.2 易感度模型数据输入

模型的具体各参数设置如表2．代入式(7)得

(8)

暴露接触时间按照乘客在车站对应区域的停留时间估算，文献[21-22]指出，乘客从进入车站到乘车全过程大致需要3～5 min，从下车到出站的时间约为3 min，因此，模型以乘客在站厅(上车和下车)及站台各停留2 min计算．

表2 易感度参数设置

3.3 客流调控仿真分析

3.3.1 基础方案

未施加防疫客流控制方案时，运行模型后可得3个区域承载人数随时间变化关系，如图4．承载人数曲线变化原因分析如下．

图4 基础方案的承载人数Fig.4 The number of passengers under basic scheme

1)站厅．由于各服务节点(如安检机)的服务效率有限，随着乘客(进站及出站乘客)到达区域的变化量大于设施的服务能力时，站厅非付费及付费区域会呈现拥挤排队，滞留乘客数随之增加，到达区域承载上限后，进站乘客会受到相应限制．

2)站台层．该区域的承载客流随车辆到达乘客上下车的交替呈现周期性增加和消散过程．

在3 600 s的统计区间内，每2 min输出1次区间承载人数数据，并将人数取整可得：站厅非付费区的平均承载人数为763人，最大承载人数为 1 197 人；付费区的最大承载人数为83人，平均承载人数为26人；站台层的最大承载人数为98人，平均区域承载人数为22人．代入式(8)可得站厅非付费区易感度平均值为0.284 662 2%，付费区易感度平均值为0.012 709 0%，站台易感度平均值为0.005 437 5%．

3.3.2 限制进站客流量

将进站客流限制比例作为关键变量，在模型中设置参数限流率进行仿真．在当前设置下，考虑乘客限流比例过大对乘客出行的影响．考虑到防控疫情要求，人与人之间距离至少为1 m，则应满足客流密度≤1人/m2．经试验，设置限流比例为0.5时，高峰时间内区域最大承载人数约为600人，基本满足要求，所以选择限流率为0.5，仿真得到3个区域的承载人数如图5．

图5 限制进站客流量的承载人数Fig.5 The number of passengers under flow control

将图5与基础方案对比可见，对进站乘车客流限制的主要影响区域为站厅非付费区域，当设置进站客流限流比为0.5时，站厅非付费区的承载人数下降至516人．经计算，非付费区的易感度降至0.192 543 4%，付费区易感度降至0.012 418 8%．

3.3.3 控制服务设施数量

考虑到疫情防控需要减少接触人数以降低感染概率，研究调整闸机数量(即减少进站闸机数和增加出站闸机数)对承载人数的影响．结果如图6．

图6 控制闸机数量的承载人数Fig.6 The number of passengers under controlling auto fare collection (AFC)

将图6与基础方案对比可见，当进站闸机数减少至5个，出站闸机数增至6个时，站厅付费区的最大承载人数减少为68人．计算得到站厅付费区易感度降至0.010 714 0%．

3.3.4 延长站厅走行流线

疫情期间可以通过设置铁栏或地面分隔标记来增加绕行距离．但非付费区域绕行距离的增加，会降低进站乘客速率及流量．绕行距离过长，会挤占站厅区域其他设施空间，影响乘客安全和行动效率．研究分析延长非付费区安检至进站闸机走行距离，结果如图7． 可见，当通道延长10 m时，非付费区的承载人数增加．计算得到站厅非付费区易感度增加至0.352 943 0%，付费区易感度下降至0.011 490 5%，站台易感度减少至0.004 609 8%．结果表明，延长绕行距离可以有效减少上车人数，但同时也存在站厅易感度上升的风险，需要考虑排队乘客间距影响．

图7 延长走行流线的承载人数Fig.7 The number of passengers under extending the streamline length

3.3.5 增加地铁发车频次

增加地铁发车频次是为了控制站台区域的等候流量和减少车内载客率，模型在保持总下车人数不变的情况下，将发车间隔周期从110 s变为100 s进行仿真，结果如图8．由图8可见，当保持总下车乘客数基本不变时，增加发车频次主要影响的是站台乘客出站以及付费区乘客排队人数，这是由于缩短发车间隔后，下车乘客尚未及时出站．计算得到站厅付费区易感度下降至0.009 413 5%，站台易感度下降至0.005 432 2%．因此，在下车总人数基本不变的情况下，采用增加发车频次措施时还需综合考虑其他因素．

图8 增加地铁发车频次的承载人数Fig.8 The number of passengers under increasing train frequency

根据以上研究结果，将4种控制方案在地铁站3个区域的防疫控制结果进行汇总，如表3及图9．结果表明，防控措施对不同区域感染概率的影响各有针对性．限制进站客流量对于降低非付费区易感度较为有效，增加地铁发车频次对降低付费区易感度较为有效，对于降低站台层易感度较为有效的是延长站厅走行流线．但采用不同策略时还需要考虑对地铁站其他区域的影响，如延长走行流线时需控制排队乘客间距，增加地铁发车频次需要综合考虑下车客流的影响．

表3 不同方案运行结果的比较

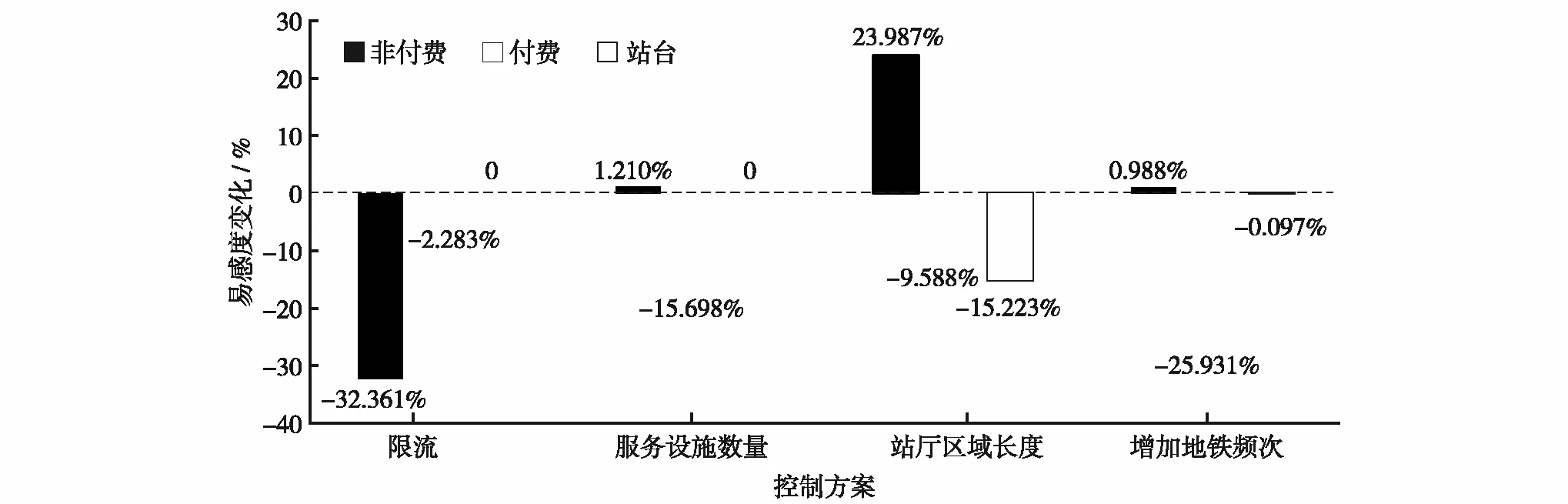
图9 4种措施下的易感度优化对比图Fig.9 Comparison chart of susceptibility optimization under four measures

4 结 论

考虑新冠疫情对地铁站客流调控的影响，建立地铁客流防疫调控的系统动力学模型，① 利用该模型输出结果分析4种不同调控措施对站内承载人数控制的效果．结果表明，基于“流”的系统动力学建模在分析客流组织策略问题方面可行有效；② 仿真结果表明，限制进站客流量对降低非付费区易感度较为有效，增加地铁发车频次对降低付费区易感度较为有效，延长站厅走行流线对站台层易感度降低较为有效．当采用不同的策略时也需要综合考虑其对其他区域的影响，必要时需额外增加辅助手段，如延长走行流线时需控制排队乘客间距．下一步研究可利用实时客流及相关换乘数据对模型的实用性和精度进行优化.