基于人工蜂群算法优化SVM 的鱼类毒性预测模型

鄂 旭，周 艺，李俏竺

（渤海大学 信息科学与技术学院，辽宁 锦州 121013）

0 引言

鱼类对水环境的变化十分敏感，当水体中的农药、污染物等化学物质到达一定程度时，会对鱼类造成一些不良影响和危害，包括急性毒性、慢性毒性、胚胎毒性及致畸性.因此，对各类化学物质的结构特性及其对环境影响的分析就显得十分重要.在安全评价中，通常只对急性毒性进行评价，而半致死浓度（LC50）则是衡量急性毒性的指标.

预测LC50浓度不仅可以为测定化学物质毒性强度、测试水体污染程度、检查废水处理的有效程度做出贡献［1］，也可以为制定水质标准、评价环境质量和管理废水排放提供环境依据.近年来，大多数学者采用定量构效关系（QSAR）的手段来预测化学物质的急性毒性［2］.其中，多维构效关系等价于多元线性回归问题，因此该手段在处理非线性关系时存在一定局限性.支持向量机（Support vector machine，SVM）是基于Vapnik提出的统计学习理论和结构风险最小化原理而建立的一种机器学习方法［3］，被认为是高维度、非线性情况下进行分类和回归的最佳方法，已经在不同领域和学科中被广泛应用.

本文在支持向量机的理论基础上，利用人工蜂群算法（Artificial bee colony algorithm，ABC）对支持向量机的核函数参数和惩罚因子进行优化，建立了一种ABC-SVM鱼类毒性LC50预测模型.这为快速、准确地预测各种化学物质中的鱼类毒性LC50浓度提供了一种新的可行方法，避免了人工使用化学方法进行分析预测的繁琐性和低效性.

1 支持向量机原理

设训练样本集为(x1，y1)，(xi，yi)，…，(xN，yN)，其中xN为样本的输入值，yN为样本对应的目标值.利用非线性映射函数φ(x)将原本输入的特征空间映射到某一高维空间内，在映射后的空间内构造最优拟合函数f(x) =[ω，φ(x)]+b，其中ω为权向量，用来说明函数f(x)的复杂度，b为常数.目的是要寻找使得结构风险最小化的ω和b，上述问题可等价于：

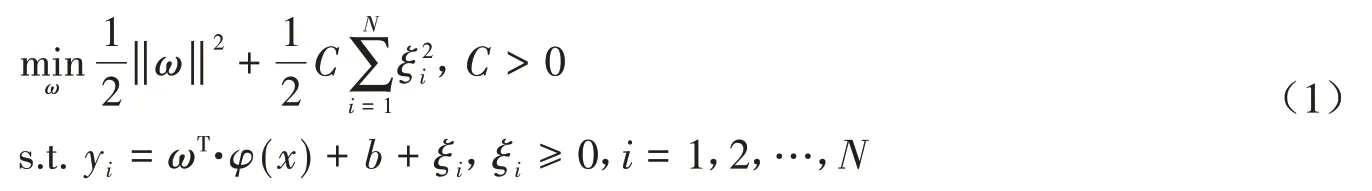
式中，ξ为松弛变量，C为惩罚因子，N为样本数，其对应的Lagrange函数为：

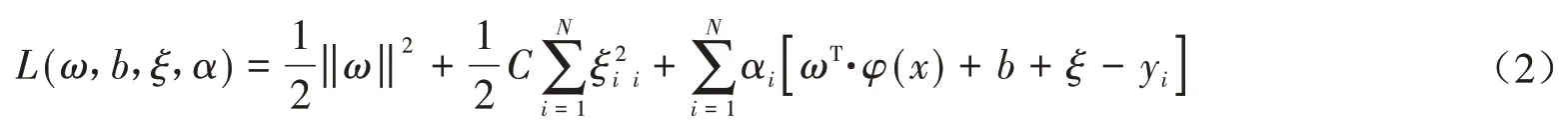
根据KKT（Karush-Kuhn-Tucker）最优条件：

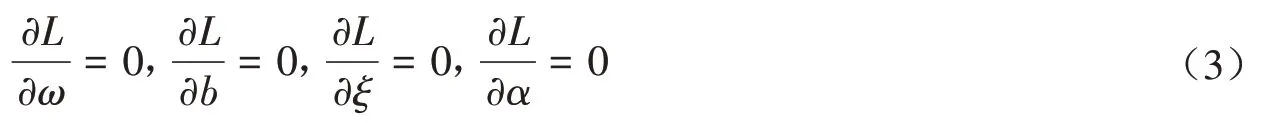
可得条件：

定义核函数k(x，xi)满足Mercer条件，进行消元计算，消去ξi和ω后，得到线性方程组为：

其中，Qij=K(xi，xj)，i，j= 1，2，…，N；e=[1，1，…，1]T；α=[α1，α2，…，αi]T；I为单位矩阵.最后可得回归决策函数为：

对于公式（5）中的核函数k(x，xi)来说，本文使用的核函数为径向基核函数（Radial Basis Function，RBF），RBF核函数生成模型的泛化能力最佳，且比多项式核函数取值简单，即：

2 人工蜂群算法

人工蜂群算法（Artificial bee colony algorithm，ABC）是Karaboga［4］在2005年通过模仿蜜蜂的采蜜行为而提出的一种优化算法.该算法只需要对问题进行优劣的比较而不需要了解问题的特殊信息，在很大程度上避免了陷入局部最优解问题，具备比传统优化方法更好的优化性能［5］，具有控制参数少、计算复杂度低、易实现的特点.

标准的ABC算法将人工蜂分为三类：采蜜蜂、跟随蜂和侦查蜂［6-7］.蜂群的整体目标就是寻找富含花蜜量最多的蜜源.三种蜂分别在不同的阶段完成任务，采蜜蜂的任务是利用当前蜜源信息寻找到新的蜜源，并将该信息传递给跟随蜂；跟随蜂的任务是在接收到采蜜蜂传递的信息后，依据该信息寻找新的蜜源；侦查蜂的任务是在蜂房附近随机地寻找一个新的有价值的蜜源.

标准的ABC算法将优化问题的求解过程看作是在D维搜索空间中进行搜索的过程，将新生成的解和原来的解作比较，并采用贪婪选择策略保留较好的解.假设问题的解空间维度为D，采蜜蜂与跟随蜂的个数为SN，采蜜蜂与跟随蜂的个数与蜜源相等.每个蜜源的位置代表一个可能解，蜜源的花蜜量对应相应解的适应度值.适用度值用来衡量当前蜜源和原来蜜源的优劣，适应度值越高蜜源的质量越优.一个采蜜蜂对应一个蜜源，则与第i个蜜源相对应的采蜜蜂的搜索公式为：

其中i= 1，2，…，N，d= 1，2，…，D，r是区间[-1，1]上的随机数，k是除了i以外的任意蜜源，k≠i.

采蜜蜂完成搜索任务后回到蜂巢，将搜索得到的蜜源信息传递给跟随蜂.跟随蜂获得蜜源信息后，根据适应度概率选择一个蜜源，跟随蜂按照与采蜜蜂相同的搜索方式，对原始解的邻域进行搜索，适应度概率公式为：

其中，pi为第i个蜜源被选择的适应度概率，fiti为第i个蜜源的适应度值.适应度值十分重要，其用来衡量当前蜜源和原来蜜源的优劣，计算公式为：

其中，fi为第i个蜜源的目标函数值.

在全部的采蜜蜂和跟随蜂完成对整个解空间的搜索任务后，如果某个蜜源的适应度值，在limit（控制参数“limit”，用于控制蜜源被改进的次数）次内没有被提高，则舍弃该蜜源位置对应的解，从而与该蜜源对应的采蜜蜂转变为侦查蜂，继续搜索新的蜜源，侦查蜂的搜索公式为：

其中，xid是第i个蜜源的第d维的值，d∈{1，2，…，D}，r是区间[0，1]上的随机数，xmind和xmaxd是第d维的下界和上界.

3 ABC-SVM鱼类毒性预测模型

在ABC算法中，以支持向量回归机的平均均方误差（MSE）为目标函数，以惩罚因子和核函数参数的参数组合(C，σ)为寻优目标，在寻优过程中，三种类型的蜜蜂通过完成各自的搜索任务，最终在解空间寻得最优解，最后利用得到的最优蜜源(C，σ)构建ABC-SVM鱼类毒性预测模型，具体步骤如下：

步骤一 参数初始化.需要进行初始化的参数包括：蜂群规模和蜜源数量NP、蜜源最大循环次数limit、最大迭代次数maxC、惩罚因子和核函数参数的参数组合(C，σ)的取值范围.

步骤二 设置适应度函数.由于优化支持向量机参数的目的是为了减小其预测误差，因此使用支持向量机回归预测的平均均方误差（MSE）作为优化的目标函数值，即：

其中yi是鱼类毒性的真实值，ŷi为鱼类毒性的预测值，n为训练样本的个数.按照公式（10）来计算其适应度值，当fi≥0时，平均均方误差越小，适应度值fiti就越大.

步骤三 采蜜阶段.采蜜蜂按照公式（8）对蜜源(C，σ)进行搜索工作，通过比较可能解的适应度值，对蜜源进行优选.

步骤四 跟随阶段.跟随蜂根据适应度概率公式（9）选择要进行搜索的新解.

步骤五 侦查阶段.判断蜜源循环次数是否超过设定值limit，若超过，则该蜜源不能被继续优化，跟随蜂放弃该解，侦查蜂利用公式（11）随机产生一个新解.

步骤六 判断是否超过最大迭代次数maxC.若超过，则模型训练结束，否则返回步骤三继续进行搜索.

综上所述，图1为本文建立的ABC-SVM鱼类毒性预测模型流程图.

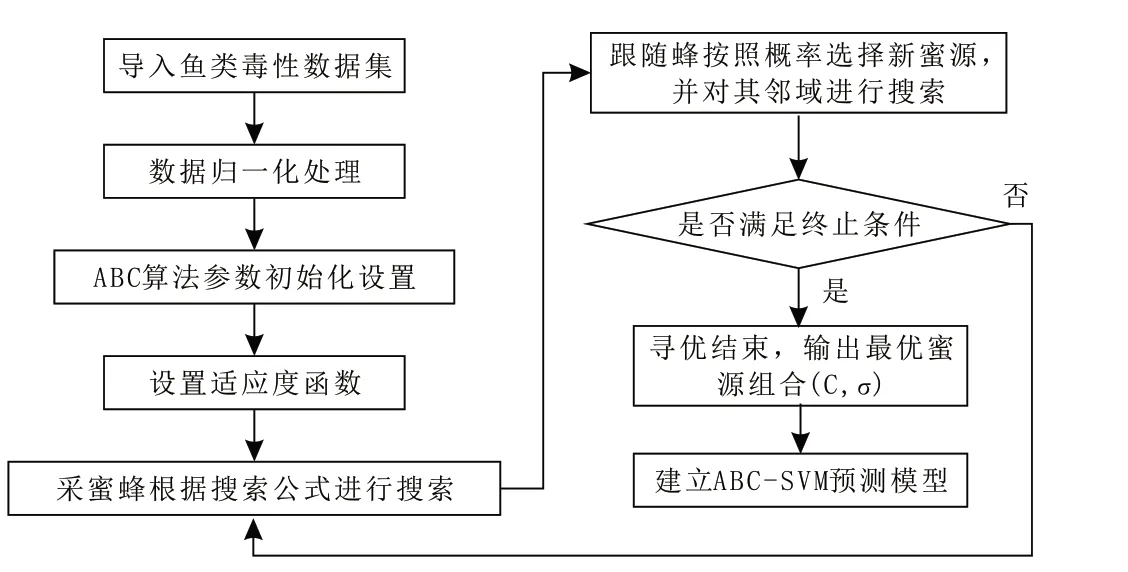
图1 ABC-SVM鱼类毒性预测模型流程图

4 仿真实验

4.1 数据准备与预处理

采用本文提出的ABC-SVM模型对908种化学物质所含有的鱼类毒性LC50浓度进行预测.本文所用数据来源于UCI数据库，由Davide Ballabio等人分析整理所得（http：//archive.ics.uci.edu/ml/datasets/QSAR+fish+toxicity）［8］.该数据集共908组数据，每组数据共有六个属性（自变量），均为化学物质的分子描述符，分别是：MLOGP（分子特性）、CIC0（信息指数）、GATS1i（2D自相关）、NDSSC（原子型计数）、NDSCH（原子型计数）、SM1_Dz（Z）（2D矩阵）.以6个量子化学参数作为模型的输入变量，以半致死浓度（LC50）作为模型的输出变量.利用前800组数据对ABC-SVM模型进行训练，将后面的108组数据放入训练好的模型中进行仿真预测.

本文的实验环境为：Windows10 64位，CPU 为AMD A8-7100 Radeon R5，8 Compute Cores 4C+4G 1.80 GHz，MATLAB2020.在开始进行实验前，先对实验数据进行极差归一化处理，将所有数据归至［-1，1］区间内.然后对ABC算法进行初始化参数设定，通过多次调试，ABC算法初始化时控制参数的设置如表1所示.

表1 ABC算法初始化控制参数设置

4.2 实验结果与对比分析

利用ABC-SVM模型对鱼类毒性LC50浓度进行预测的实验数值结果如表2所示，为了避免一定的偶然性，确保实验的严谨性，实验共运行10次，最终结果取10次结果的平均值.从表2中可知，利用ABC-SVM模型的预测准确率已达到了85.166%，在迭代多次的情况下，运行时间共46.518 019 3秒，初步体现了利用ABC-SVM模型进行预测的精准性和高效性.

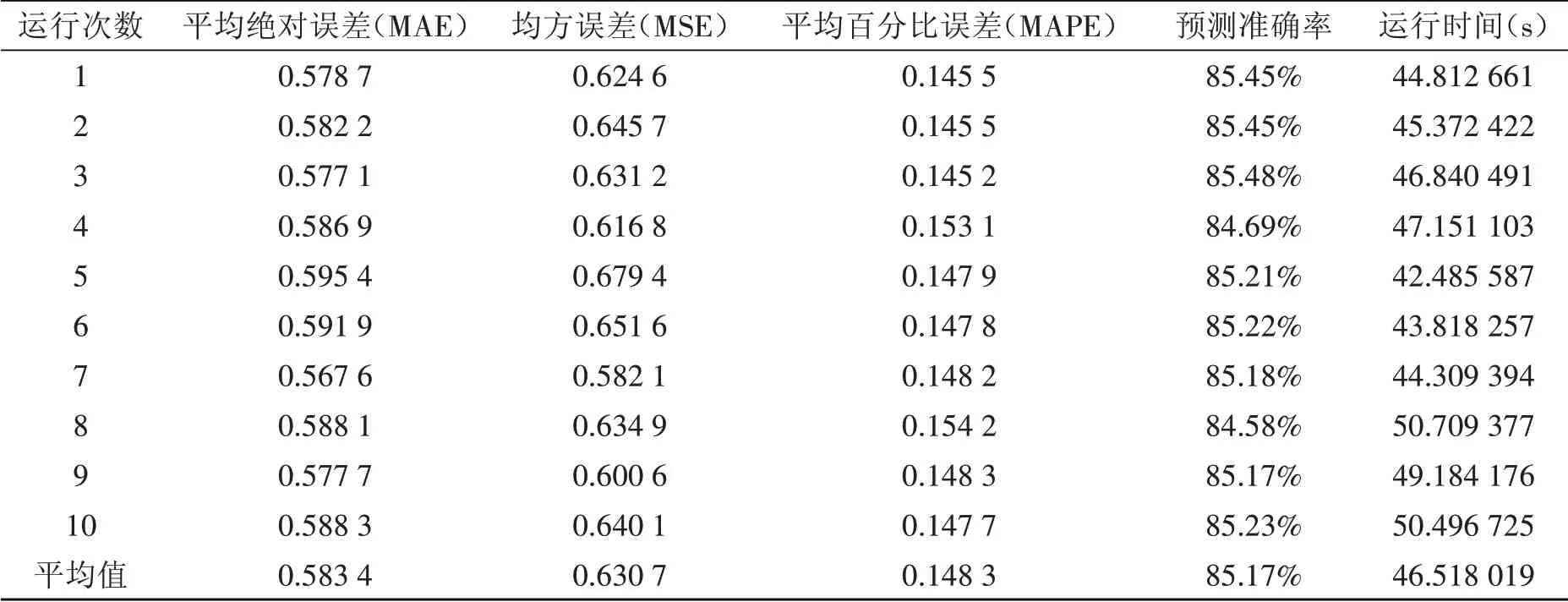
表2 ABC-SVM模型对鱼类毒性LC50浓度进行预测的实验数值结果

为了能够进一步直观突显出ABC-SVM模型较好的拟合预测效果，本文选取了GA-SVM模型［9］、PSOSVM模型、ABC-SVM模型和原SVM模型四个模型分别进行拟合，对鱼类毒性进行预测.图2为4种模型的拟合预测曲线.从图2中可以看出，ABC-SVM模型的拟合曲线更接近真实值，原SVM模型与真实值的偏差较大，PSO-SVM模型和GA-SVM模型较原SVM模型相比，偏差较小，但不如ABC-SVM模型的拟合预测效果好.

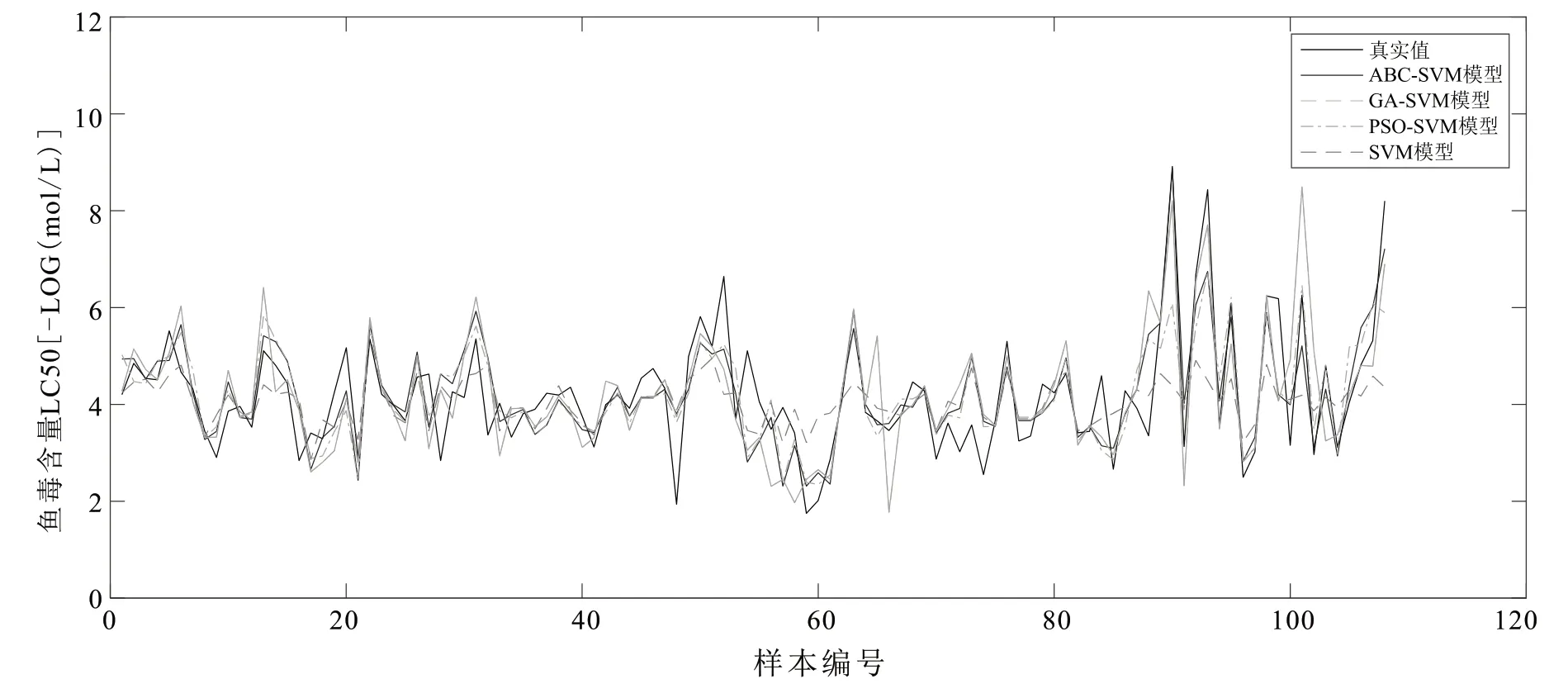
图2 四种模型的拟合、预测曲线

通过比较四者平均绝对误差（MAE）、均方误差（MSE）、平均百分比误差（MAPE）、预测准确率、运行时间等方面的具体数值来判断四个模型的优劣.其中，每种模型所进行的预测实验分别独立运行十次，最终结果取其平均值，对比结果如表3所示.从表3中可以看出，三种结合了优化算法的SVM模型的MAE、MSE、MAPE均小于默认参数的原SVM模型，平均预测准确率都高于原SVM模型，证明了三种优化后的模型效果均比原模型好.在三种结合了优化算法的SVM模型中，在种群规模大小和最大迭代次数相同的情况下，GA-SVM预测模型的平均运行时间太长，近似等于其他两种模型的3倍运行时间，运行效率较低，浪费内存空间.PSO-SVM模型较GA-SVM模型相比，误差更小，具有更高的平均预测准确率，并大大提升了平均运行时间，模型表现较GA-SVM模型好.而ABC-SVM模型在三者中拥有最高的平均预测准确率，且运行10次的平均时间最短，与GA-SVM模型、PSO-SVM模型相比较，具有较高的预测精度和运行效率.表3中的对比结果与图2所表明的结果相吻合，明确地验证了ABC-SVM模型较好的预测效果，因此在对鱼类毒性LC50浓度进行预测时，优先考虑使用ABC算法对支持向量机参数进行优化，以此建立相应的预测模型.

表3 默认参数的原SVM模型、GA-SVM模型、PSO-SVM模型、ABC-SVM模型的对比实验结果

5 结论

本文主要研究了人工蜂群算法对支持向量机控制参数进行优化的基本原理，建立了ABC-SVM的鱼类毒性LC50预测模型，以均方误差（MSE）作为适应度值，利用极差归一化的方式对数据进行归一化处理，使用ABC-SVM模型对鱼类毒性LC50浓度进行预测，预测准确率达到了85.17%，运行时间仅共46.518秒.通过对比实验分析，ABC-SVM模型效果的预测准确率高于PSO-SVM模型和GA-SVM模型，并具有更高的运行效率.这为快速、准确地预测各种化学物质中所含鱼类毒性LC50浓度提供了一种新的可行方法，避免了人工使用化学方法进行分析预测的繁琐性和低效性.