半导体量子点/马约拉纳纳米线Aharonov-Bohm干涉仪中的热电效应
王宇鹏
(渤海大学 学报编辑部,辽宁 锦州 121013)
0 引言
近十几年来,介观系统中的热电效应(Thermoelectric effect)得到了广泛的理论和实验研究,这些系统包括单个或多个半导体量子点、多种半导体材料制备而成的纳米线、纳米管等[1-2].低维量子系统中热电效应的研究动机主要有两个:一是尺寸持续降低的器件中的电流会产生大量的废热而影响其正常运行.如果能利用热电效应将这些热能转换为电能无疑是非常有意义的.另一个是大量的实验和理论工作已经说明,低维量子系统中的热电效应相比于宏观体材料中的有独特的性质,例如可以控制电子态密度的尖峰位置和高度、离散化的电子能级、电子与电子之间的库伦相互作用或者声子的散射过程等来提高热电势的大小和热电转换效率[1-2].最重要的热电效应物理量为热电势(塞贝克系数),定义为S= -ΔV/ΔT,其中ΔV为施加在系统两端的温度差ΔT产生的电势差.电能与热能之间的转换效率由热电优值因子ZT=GS2T/κ来表示,其中G为线性电导,T为系统的平衡温度,κ为电子和声子贡献的热导率之和.根据维德曼-弗兰兹定律(Wiedemann-Franz law),宏观热电材料中电子和声子的热导率满足G/κ= 3e2/(πkB)2T,即电导率的增大必然伴随着声子热导率的增加,因此ZT的值很难超过1,极大限制了热电器件和材料的工业应用.在低维量子系统中,维德曼-弗兰兹定律会被电子之间的库伦相互作用、量子干涉效应或特殊的器件设计等机制所打破,使这种器件和材料的广泛应用成为可能[1-2].
除了在能源方面的应用,近年来热电效应也被提出用于探测马约拉纳束缚态的存在.在凝聚态物理中,马约拉纳束缚态表示马约拉纳费米子在纳米管两端形成的一对准粒子激发[3-4].这种马约拉纳束缚态不再是费米子,而是服从非阿贝尔统计的任意子[3-4],由其制备而成的量子比特除了具有通常固态器件中量子比特的一切的优点之外,还有更好的“纠错”能力,因而成为容错拓扑量子计算领域中新的研究热点[3-7].以往的研究证明,如果马约拉纳束缚态与两个电极之间的量子点相互作用,其电子-空穴对称性将被打破.例如,C.Y.Hou等[8]人指出,与承载马约拉纳束缚态的拓扑超导纳米线相互作用的量子点中的热电势满足莫特公式.其原因是马约拉纳束缚态的电子-空穴对称性被打破致使正、负载流子在空间发生分离而增大了热电势.这个理论结果也可以用来测量马约拉纳束缚态的温度.日本学者Leijnse理论证明[9],量子点与马约拉纳束缚态之间的相互作用能够破坏体系的电子-空穴的对称性,从而加强热电信号而用来探测马约拉纳束缚态的存在或分离出马约拉纳束缚态的耗散衰变信息.也有欧洲的学者研究了与两个电极和马约拉纳束缚态相互作用的量子点系统中热电势符号改变的效应[10],并用其来探测马约拉纳束缚态的存在.
近年来,一些研究者提出了利用量子点AHARONOV-BOHM干涉仪中的干涉效应对马约拉纳束缚态进行操控和测量[11-13].例如,若具有马约拉纳束缚态的纳米线与两个电极耦合而形成多通道结构,只要束缚态与干涉仪的耦合强度相同,系统的微分电导值即为零,与其它参数无关,而且零偏压下电导的值在任何情况下都与穿过干涉仪中的磁通量无关[11].如果量子点的电子能级与马约拉纳束缚态的能量相同,电导的震荡周期在电子-空穴的对称性作用下为π[11].在马约拉纳束缚态与量子点直接耦合的干涉仪结构中,研究者发现当量子点的能级为零时,电导会在马约拉纳束缚态的作用下形成三个尖峰[13],而且电子在不同输运通道中隧穿时会发生相干干涉,从而电导的线形为典型的非对称Fano峰形式[13-14].研究者们已经证明,多通道系统中电子相互干涉而产生的Fano[13-15]效应会破坏电子-空穴的对称性,从而显著提高热电势的值,并在一定条件下造成热电势符号的翻转,即电子-空穴两类载流子的转换.虽然马约拉纳束缚态影响下的电子输运性质已经在量子点干涉仪系统(如图1所示)中得到了一定的研究[11-13],但这种系统中的热电效应还很少被考虑,是本文所要研究的内容.本文的计算结果发现,量子点干涉仪中马约拉纳束缚态与量子点之间的相互作用将削弱Fano干涉效应对热电效应的影响.热电势的绝对值随量子点与马约拉纳束缚态之间的相互作用增强而可能会变小,并在一定的量子点能级范围内改变符号,为探测马约拉纳束缚态的存在提供了新的判据.马约拉纳束缚态之间的直接相互作用使得热电势对量子点能级的曲线中重新出现符号相反的尖峰,并造成其符号的翻转.作为对比,本文还考虑了干涉仪中的量子点与另一个量子点中的常规费米子相互作用的情况,以说明马约拉纳束缚态性质的独特性.
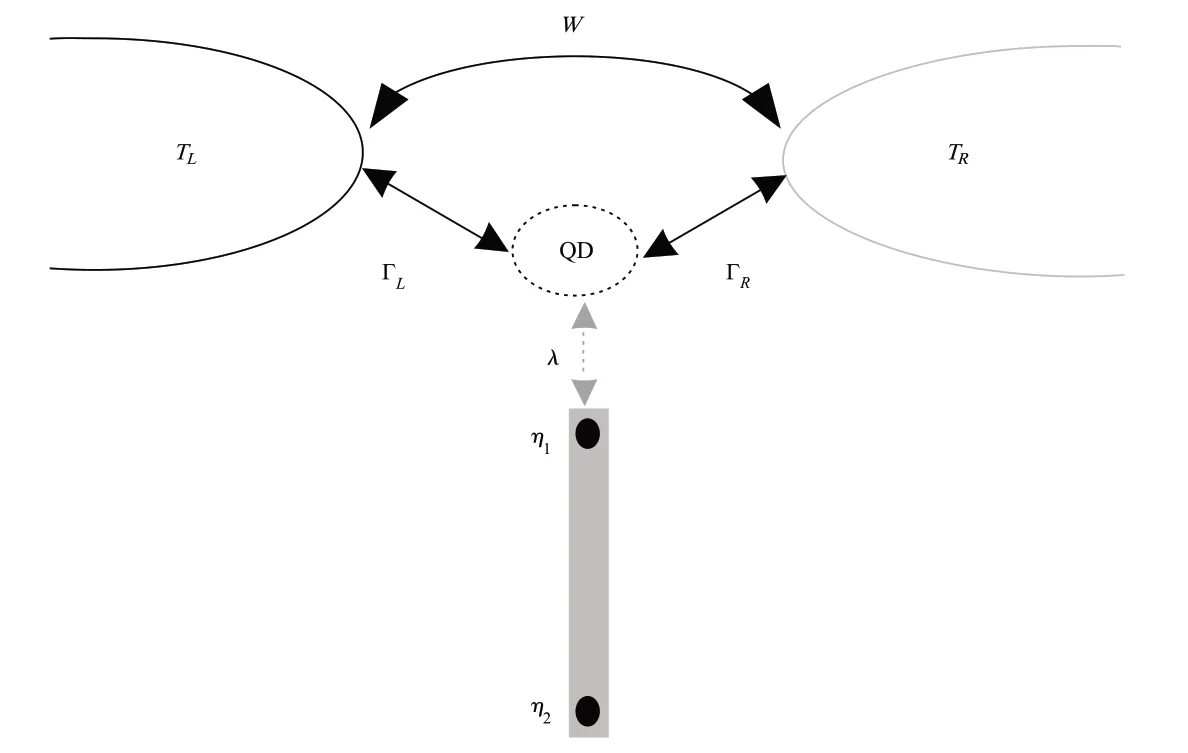
图1 与温度分别为TL和TR的两个普通金属电极相耦合、并与超导纳米线一端的马约拉纳束缚态相互作用的量子点干涉仪.量子点与两个电极的耦合强度分别为ΓL和ΓR,与马约拉纳束缚态的模η1的耦合强度为λ.两个电极之间的直接耦合强度为W
1 理论模型与计算方法
如图1所示,左右两个普通金属电极分别与单量子点耦合,并通过隧道结而直接相互作用,纳米线一端的马约拉纳束缚态与量子点中无自旋的电子耦合,系统的二次量子化哈密顿量可写为[10,13,15]
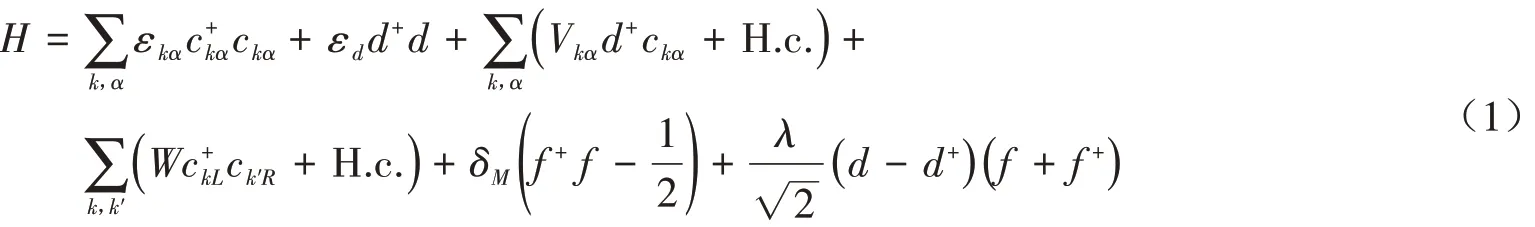
其中W为左右两个电极之间的直接隧穿耦合强度和ckα分别为电极中能量为εkα的电子的产生和湮灭算符.d+和d分别为量子点中能量为εd的电子的产生和湮灭算符.Vkα代表量子点和电极中电子之间的耦合强度.公式(1)中最后两项表示将马约拉纳束缚态变换为常规费米子后的哈密顿及其与量子点之间耦合,其中马约拉纳束缚态与量子点的耦合强度为λ,两个束缚态之间的耦合强度为δM.f为常规费米子的湮灭算符,满足反对易关系,{f,f+} =ff++f+f= 1.
流过系统的电流和热流分别为[10,15]

其中积分Ln(n= 0,1,2)为[10],
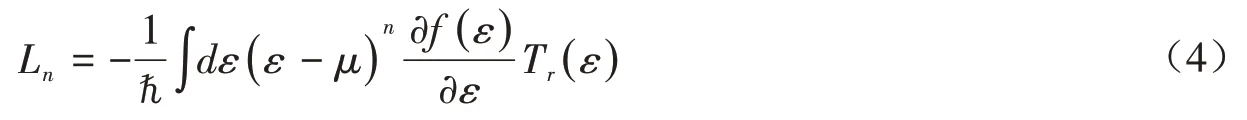
上式中的平衡费米分布函数为f(ε) =[exp[(ε-μ)/kBT]+ 1]-1.由上面的表达式可以得到所要研究的热电物理量,热电势为S= -( 1/eT)L1/L0,G=e2L0.

热电优值因子(Figure of merit)[16],

公式(4)中的Tr为电子的透射系数,可以用系统的格林函数表示.由运动方程方法,系统的推迟格林函数的表达式为[10,15],
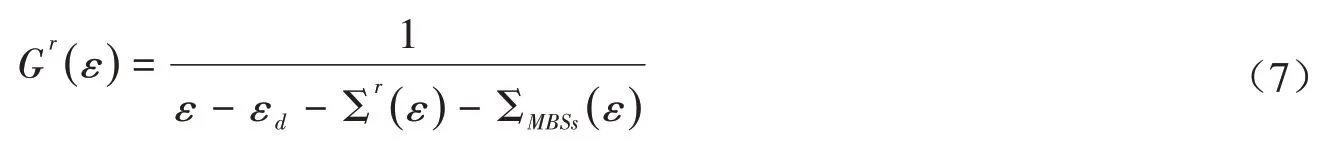
上式中量子点与电极相互作用的自能为,

其中总线宽函数Γ=ΓL+ΓR,Γ͂=Γ/( )1+x,α=4ΓLΓR/Γ2.x=π2W2ρL ρR为两个电极之间直接耦合的强度,ρL R为左/右电极中电子的局域态密度.ΣMBSs为量子点与马约拉纳束缚态相互作用的自能,其表达式为[13,17]

其中K= 1/2(ε-δM+i0+)+ 1/2(ε+δM+i0+),以及,

根据上面的结果,可以得到透射系数为[13,17],
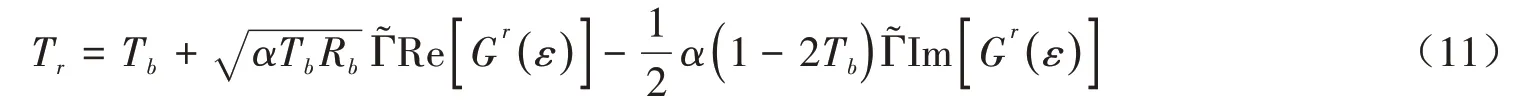
2 结果与分析
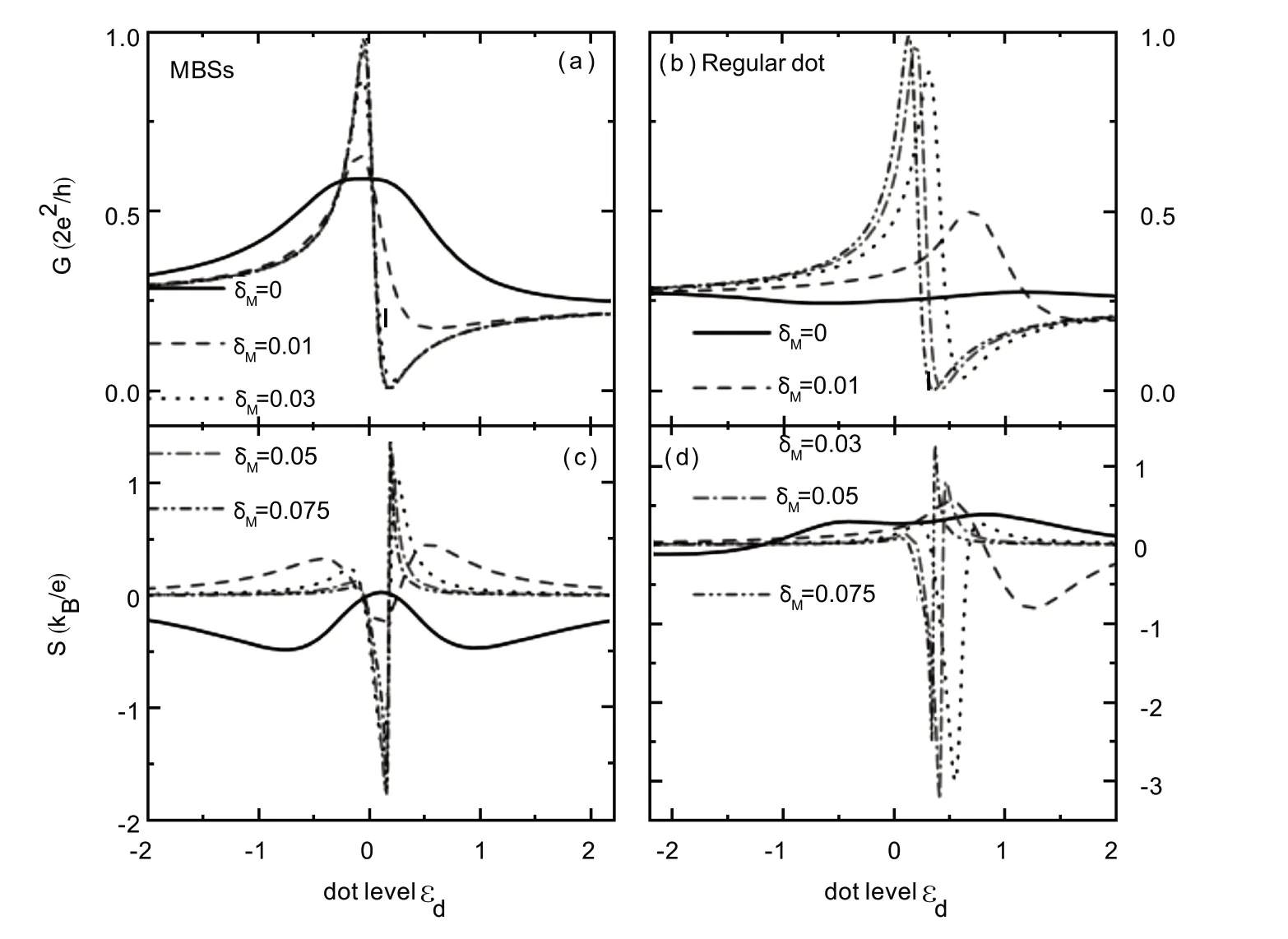
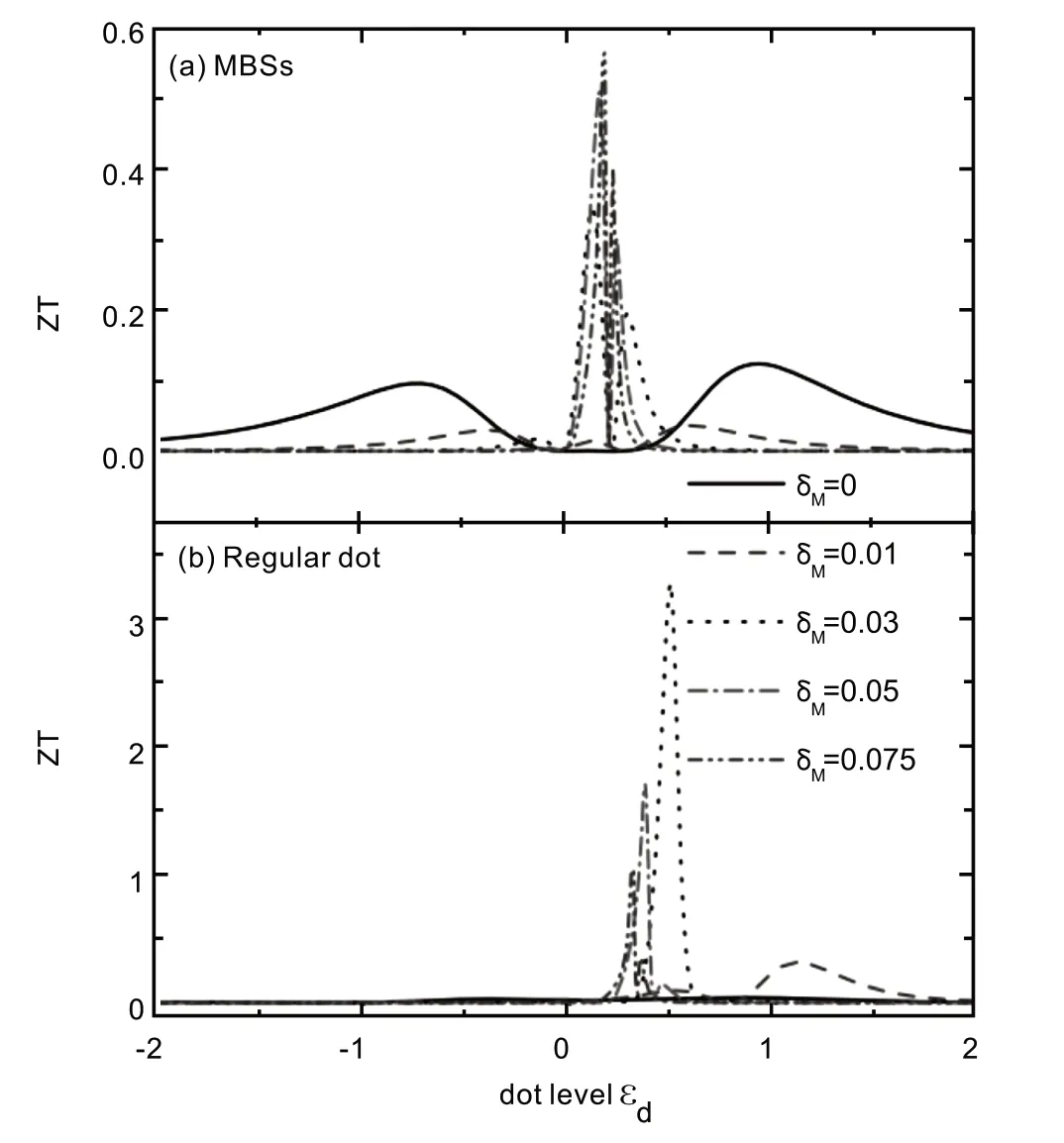
在数值计算中,我们取电极中的半带宽D≡40为能量单位,并取ΓL=ΓR≡0.1D,系统平衡温度T=0.0025D.如果量子点不与马约拉纳束缚态或另一个量子点相耦合且当Tb= 0时,本文研究的器件成为量子点仅与两个普通金属电极耦合的简单结构,此时的透射系数有典型的单个洛伦兹共振峰线形[17].共振峰的中心位于电子入射能量ε=εd之处,它的宽度为Γ,大小达到其量子极值Tr= 1[17],这个结果没有在本文给出.当背景透射概率0 当干涉仪中的量子点与马约拉纳束缚态相互耦合时(λ≠0),由图2(a)中的细点线和虚线可知,反对称的Fano线形被破坏,并且零能级的电导率值迅速减小为常数G(εd= 0 )≡0.6e2/h.值得指出的是,当λ≠0且W= 0时,以前的研究工作已经发现量子点与马约拉纳束缚态之间的相互作用将导致电子的电导为其量子极值的一半,即G(εd= 0 )=e2/2h,是马约拉纳束缚态存在的典型表现,最初是在文献[17]中的无自旋、无库伦相互作用及零温的条件下得到的.本文发现当W≠0时,零能的电导值会由于背景散射通道的存在而增大,但仍保持为常数,同样可以当做马约拉纳束缚态存在的判据.当量子点与常规费米子耦合时,图2(a)中的粗点线和虚线说明原来的共振峰变为了谷,并且也趋近于一个常数G(εd= 0 )≈e2/4h. 当量子点与马约拉纳束缚态耦合时,透射系数出现三个峰,对应的三个电子态.在每一个共振态处,透射系数都有相同形状的非对称线形.在不同的能量处,电子隧穿通过系统的概率不同,透射系数峰的高度相应不同.由于电导是透射系数在费米能级附近对电子能量的积分结果,因此这些透射系数的峰在温度较高的情况下不能在电导的曲线中出现.当λ= 0时,图2(b)中的热电势值在能级εd= 0处有一个零点,并在其两侧各有一个符号相反的峰.其产生的原因如下[8-10,16]:假设左侧电极的温度高于右侧电极,结果在左侧电极中更多的电子被激发到化学势μ以上,同时更多的空穴处于能量低于化学势的状态.在右侧温度较低的电极中,只有较少的电子被激发到化学势以上,在化学势以下空穴的数目也相对左侧电极少.当量子点能级高于化学势μ时,左侧电极中能量与量子点能级相同的电子运动到右侧电极中,造成负的热电势.在量子点能级低于化学势时,左侧电极中的空穴运动到右侧电极,结果热电势的符号翻转.在量子点的零能级位置处,相同数量的电子和空穴向相反方向运动,其电流或电动势相互抵消,因此热电势为零.当λ≠0时,热电势的值迅速变小.当量子点与马约拉纳束缚态的耦合较弱时,两个量子点之间耦合造成的干涉效应较强,因此热电势在峰的两侧各形成一个反共振的谷.随着λ的增大,量子点与马约拉纳束缚态的相互作用产生的影响占优势,因此两个谷消失,热电势形成一个宽的峰,如图中的细点线和虚线所示.如果量子点与常规费米子相互作用,热电势的零能级峰将变得更宽,如图中粗虚线和点线所示.图2(c)给出λ值不同时热电优值因子随量子点能级的变化关系.当量子点与马约拉纳束缚态相互作用时,ZT的值随λ的增加而迅速减小,同时其中心的峰分裂为两个,分别向低能和高能方向移动,如图中的细线所示.然而当量子点与常规费米子相互作用时,ZT的中心峰位置不发生移动,仅仅是峰的高度降低. 图2 不同的马约拉纳-量子点耦合强度,及两个常规量子点的耦合强度λ条件下电导(a),热电势(b)及优质因子(c)随量子点中电子能级的变化关系.其中背景透射系数为Tb = 1/4( )x = 0.072 ,δM = 0.图中的细虚线和点线表示量子点与马约拉纳束缚态相互耦合,较粗的虚线和点线表示量子点与常规费米子,即另一个量子点相互作用 当两个马约拉纳束缚态之间存在直接耦合δM≠0时,图3(a)说明电导的值迅速增加,同时Fano效应变为主导.图3(b)中量子点与常规费米子耦合情况下的电导与图3(a)中的类似,都在较大的δM值时呈现典型的Fano共振线形.图3(c)说明当δM≠0时,马约拉纳束缚态导致的热电势在特定温度下符号翻转的现象消失.即使对于很小的耦合强度δM= 0.01,热电势也在整个量子点能级范围内发生了再次的符号翻转.当一对马约拉纳束缚态之间存在相互作用时,图3(c)表明热电势的Fano线形开始变得明显,这是由于马约拉纳束缚态之间的直接相互作用会降低其对输运过程影响.当量子点与常规费米子耦合时,热电势的不对称性变得更强,同时峰值也更大,可以用来分辨与量子点耦合的费米子类型. 图3 电导G和热电势S在不同的δM条件下随量子点能级的变化关系.其中(a)和(c)对应量子点与马约拉纳束缚态相互作用,(b)和(d)代表干涉仪中的量子点与另一个量子点相互作用的情况.其它参数为,背景透射系数Tb = 1/4,耦合强度λ= 0.1 图4给出δM≠0时量子点分别与马约拉纳束缚态(a)和常规费米子(b)相互作用情况下的热电优值因子ZT随量子点能级的变化关系.图4(a)说明,当量子点与马约拉纳束缚态耦合,随着δM的增大,热电优值因子的两个峰向零能级处移动,并最终合并为单峰,即马约拉纳束缚态造成的ZT峰分裂效应消失,热电优值因子的值变大.当量子点与常规费米子相互作用时,图4(b)表明热电优值因子的值迅速增加,同时峰向高能方向移动.当δM的值较大时,ZT的峰值能达到3左右,远远大于量子点与马约拉纳束缚态相互作用的情况.这个结果同样可以用来区分与量子点耦合的费米子类型. 图4 热电优值因子在不同的条件下随量子点能级的变化关系,其中图(a)表示量子点与马约拉纳束缚态相互作用,图(b)表示量子点与常规费米子相互作用的结构.除图中所示,其它参数与图3中的相同 本文研究了单量子点干涉仪中的热电势和热电优值因子的性质,分别考虑量子点与纳米线中的马约拉纳束缚态及与另一个量子点中的常规费米子相互作用的两种不同情况.数值计算结果表明,随着量子点与马约拉纳束缚态相互作用的增强,系统中的Fano效应被减弱,电导对量子点能级的依赖关系变为单个宽峰的结构.当二者的相互作用足够强时,零能级附近的电导峰在背景散射的作用下为G= 0.6e2/h,与没有干涉效应情况下的零能级电导峰G= 0.5e2/h的结果完全不同.而当量子点与常规费米子相互作用时,电导的峰变得更低.当量子点与马约拉纳束缚态作用时,干涉仪中的热电势迅速变小,同时发生符号转变的现象.热电势的符号翻转效应不会发生在量子点与常规费米子相互作用的系统中.当一对马约拉纳束缚态之间存在直接的相互作用时,其对热电输运性质的影响降低,从而电导恢复Fano线形,并伴随着电导峰的增加.热电势的符号在马约拉纳束缚态之间的直接相互作用下再次发生翻转,并伴随着数值的增加.当量子点与马约拉纳束缚态耦合时,热电优值因子的高能级和低能级处的峰因两个束缚态之间的直接相互作用而向零能级处移动,并最终合并为单峰.当量子点与常规费米子相互作用时,热电优值因子的值迅速增加,同时峰向高能方向移动.当另一个量子点的能级较大时,结构的不对称性增强而使得热电优值因子的峰值远远大于量子点与马约拉纳束缚态相互作用的情况,可以用来区分与量子点耦合的费米子类型.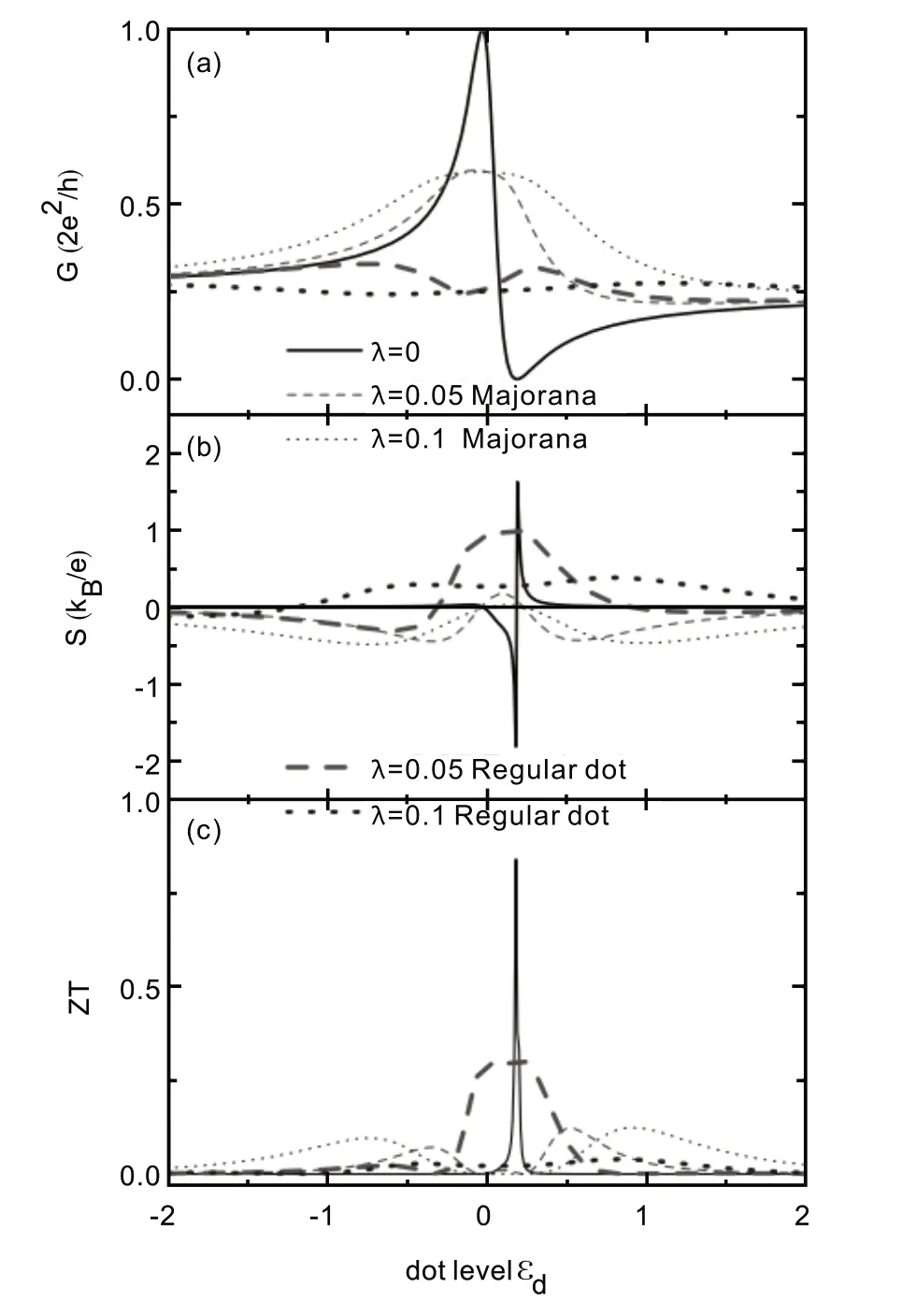
3 结论
——记上海交大领衔的科研团队成功捕获马约拉纳费米子的重大成果

