考虑相对财富的前景理论价值函数对比研究

陶刚

（贵州师范大学 经济与管理学院，贵州 贵阳 550001）

一、引言

对于人类的风险偏好的探究是更好地理解经济现象的本质出发点，本文通过行为实验数据，重点研究前景理论（Prospect Theory，简称“PT”）中的价值函数，并将模型扩展，尝试将个人财富因素纳入模型，进行对比研究。考虑了个人财富因素的模型简称“PT-RW”，其中RW代表相对财富（Relative Wealth），PT 模型中考虑的是绝对财富量变化引起的心理效应的改变，但是相对于个人财富总量的财富变化更能有效地反映相应的心理效应，即“RW（Δw）=绝对财富量的变化÷个人总财富”。具体下文从三个维度进行对比研究：一是纳入个人财富因素的价值函数模型（PT-RW）在总体解释力上是否会强于原PT 模型；二是价值函数在负定义域的凹凸性有争论，本文对此维度进行比较研究；三是正负回报的加权函数π 是否一致，即π+=π-。本文对PT 和PT-WR 的函数模型进行分析，并设计实验收集数据，对模型进行检验，计量方法选取的是普通最小二乘法（Ordinary Least Squares，简称“OLS”）与非线性最小二乘法（Non-linear Least Square，简称“NLS”）。

二、模型

PT 价值函数理论形式为：

实验问题中有一组完全正回报风险资产的问题，可以由这组问题估计出PT 价值函数的α参数。具体的有：

其中x1i与x2i为实验问题直接列出的风险资产中的两个或有状态回报，并假定心理参照点就是自己拥有的财富量，权重函数π 由于概率固定在一点上，所以作为常参数来估计，Gi为正回报风险资产问题中所诱导出的确定性等价。

纳入了个人财富因素的模型PT-RW 函数形式为：

PT-RW 价值函数形式显得复杂，但在非混合回报的情况下总能分别退化为两个简单的幂函数形式，因此在估计模型选择上同样采取了和PT 价值函数相同NLS 计量模型，只需要在变量上进行一些处理，用到实验问题中直接列出的风险资产的两个回报以及被试的财富量数据。

PT 价值函数中用参数λ 来表示损失厌恶系数，为此需要专门设计一组实验问题来估计参数λ，这个估计问题还要把预先对PT 的非混合回报情形估计出的参数α 跟β 带入，才能使用进一步估计参数λ。注意式（4）中没有权重函数，这是因为将概率值固定在0.5。关于0.5的概率划分，稍微回顾理论就可发现这样一种安排将权重函数的部分恰好消去。

其中，x1i是在实验中设定好的数据，x2i是实验诱导出的数据。

由于非线性最小二乘估计在计量软件中不报告拟合优度R2，需要在最后一组混合回报的问题中通过普通最小二乘法来比较两个价值函数对数据的解释力，只要把第一组、第二组、第三组实验问题中对PT 估计的参数α、β、λ 以及对PT-RW 估计的参数α、β 带入，生成新的变量，就可利用OLS 报告的拟合优度来比较两个模型的解释力。

三、估计方法

以正回报风险资产检验原假设H0：π1+π2=1为例。首先估计完全模型：

记为模型Full。然后将约束条件带入π1+π2=1，估计约束模型：

记为模型Reduced。分别从两次回归中记录相关统计量，然后计算：

其中RSS 代表残差平方和，df 代表自由度，n 为观测点数。再让统计量F 与其分布的拒绝域比较，即可检测原假设π1+π2=1的真伪。若检测约束条件为真，将在最后模型比较时的参数代入中使用约束模型估计出的参数。

对于原假设H0：π+=π-的检验，在有一个状态回报为零的情况下其等价于检验H0：π+=π-，现在需要把正、负回报的问题合并到一个数据集中，并生成标识变量，若为负回报标识变量TX=1，若为正回报TX=0，生成变量yi，当为正回报时其等于Gi，为负回报时等于Li，则可估计模型：

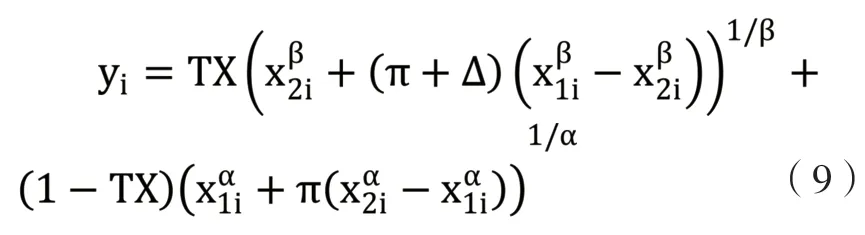
在此模型中令π+Δ 为π-，π 为π+，所以检验原假设π+=π-，进一步简化为检验参数Δ 是否为0。对于PT-RW 价值函数的估计方法可以沿用同样的思路。

四、实验设计

获取被试的确定性等价数据（Certainty Equivalent，简称“CE”）是本文研究的关键。实验经济学家强调确定性等价由实验诱导出，而不是凭被试自己口述报告的重要性。确定性等价可以理解为对一支风险资产的估值，假设一支风险资产L，你对其估值￥1000，也就是说1000是你对这支风险资产的确定性等价，在实验中如果出价1010，你就不愿意买L，而出价990，你就愿意买L，那么就说你的确定性等价在（990，1010）这个价格区间。在文献中通常用区间的中值作为确定性等价的估计值，若实验越精细，价格区间越小，那么就越逼近被试者的确定性等价真实值。本文选取贵州某大学学生作为实验被试。实验一共有两轮，一轮实验中又分为上下两节，每节时长45分钟，中间有10分钟休息时间，两轮实验间隔一周。初选被试共92名同学，剔除异常值，有80个有效反馈，其中55名男生、25名女生。

在两轮实验中需要获得两类信息，一是四组风险资产的确定性等价，二是个人财富数据。由于在资产状况变化不大的时候总可以认为人的效用是线性的，所以刻意让或有回报的数值较大，以便于更准地测定效用函数的弯曲程度。在第一轮实验中进行的是两组非混合回报风险资产问题的测试，并且在开始时，有一组预热问题让被试熟悉他们将回答的选择问题，被试也被告知选择并无对错之分，回答问题过程中可以暂停并休息。大学生没有真正属于自己的财富积累，绝大部分同学还都是靠父母资助。实验选取的是学生的学期消费作为被试财富的代理变量，因为这个数据既容易被被试自己估计，又能相对全面地反映学生消费能力，如果默认消费能力和财富有相对稳定的关系，就有理由让这个数据作为被试财富量的代理变量。

在第一轮实验中，给被试展示的两组非混合回报风险资产问题如表1所示。

表1 非混合回报风险资产确定性等价诱导问题

确定性等价的诱导过程如下：以风险资产（400，0.5，2000）为例，首先展示其均值1200，如果被试的选择偏好为（400，0.5，2000）＜1200的话，即被试在这两个资产间选择1200，那么将确定性资产1200的数值下降25%到900，若仍为（400，0.5，2000）＜900，继续下降到675，若（400，0.5，2000）＞900，那么从900上升25%到1125，重复5次后找到区间a ＜（400，0.5，2000）＜b，最后以（a+b）/2代表其确定性等价，其他组的诱导过程沿用相同办法。在第一轮中对被试进行学期消费分类问卷，除去学校必要花费，比如学费、住宿费及书费，调查个人的学期基本餐饮消费、社交活动餐饮消费、通信费、是否旅游及旅游消费、更换几次手机及相应花费、文化活动消费如演唱会及展览、衣物购买消费。学生填于问卷表上，反馈回来再对其逐项加总。

第二轮中的两组风险资产问题如表2所示。

表2 混合风险资产正回报诱导问题

其中第三组实验问题是专门设计来测试PT 价值函数中参数λ 的，（-1200，0.5，x2）表示如果有五成可能赔￥1200，那么这个博彩中赢面的奖励x2要是多少你才肯接受这个博彩，x2就是第三组问题中要诱导出的数值。第四组问题诱导出确定性等价后，将前三组问题中分别得到的PT 与PT-RW 价值函数的参数带入，生成新的变量，就可以利用OLS 来比较两个价值函数对于实验数据的拟合优度，进而看出哪个模型对数据的解释能力更强。第四组问题如表3所示。

表3 混合风险资产确定性等价诱导问题

五、实验结果

被试学生的消费数据统计显示，最大值为￥11528，最小值￥1251，均值￥4107，标准差￥2049，中位数￥3315。数据偏态为右偏，表明大部分人消费能力低，较小部分人群的消费能力高。学期消费从￥2500到￥4500的样本有54个，占总样本的67.5%。表4为第一组实验问题的NLS 参数报告，第一组中全是正回报风险资产，因此测出的是PT-RW 与PT 价值函数的参数α 及相应的权重函数。每个价值函数又分为无约束模型和约束模型来进行回归反洗，约束条件为π1+π2=1，括号中报告的是95%置信区间。NLS 参数初值设定为α=1，π1=π2=0.5。无论用PT-RW 还是PT 的价值函数，都无法拒绝原假设π1+π2=1。因此在第四组问题中PT-RW与PT 价值函数模型比较时带入约束模型的参数，PT-RW 价值函数带入α=0.5205，PT 价值函数则带入α=0.9481，可见两个价值函数估计的α 在正回报风险资产的情况下差别明显，且表现为PT-RW 价值函数模型在正回报情形下函数弯曲程度更大。

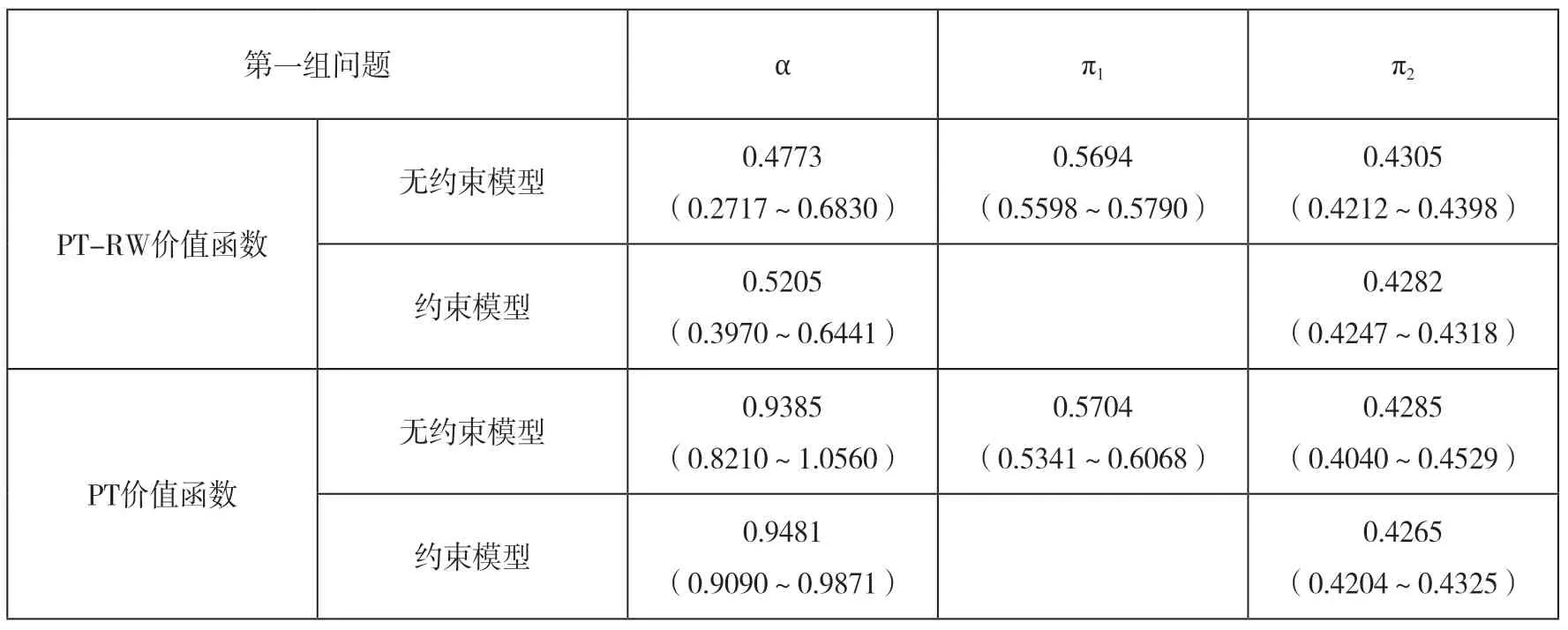
表4 正回报风险资产问题的NLS 参数估计

表5是在负回报风险资产的第二组测得的参数，仍然无法拒绝原假设π1+π2=1。两价值函数估计得到的β 差别不明显，但是比较原模型会发现若PT-RW 价值函数的β＜1，则在负定义域表现为凹函数，而PT 价值函数的β＜1，则在负定义域表现为凸函数，但总体来说相对于正定义域的函数，负定义域函数都更接近于直线。具体在第四组问题中比较两个价值函数的解释力时，代入的PT-RW 价值函数参数β 为0.9686，代入的PT 价值函数参数β 为0.9826。可见用实验数据，PT 模型NLS 结果仍然能得到负定义域函数为凸的结论，但是融入个人财富的PT-RW 模型，能让凸函数转变为凹函数。若价值函数全局为凹，那么和经典经济理论就有更优的融合度。将第一组和第二组数据结合起来测试原假设π+=π-，其中π+相当于第一组问题的π2，π-相当于第二组问题的π1。无论用PT-RW 还是PT 的价值函数都无法拒绝原假设π+=π-。在第三组问题中测得λ=1.9146。

在用OLS 方法对PT-RW 和PT 价值函数的比较中，发现PT-RW 的拟合优度为43%，大于PT 函数的拟合优度26%。且PT 的OLS 模型中截距项在5%置信水平下显著不为零，而参数π1并不显著。由此可见在本组数据中融入了个人财富数据的PT-RW 价值函数解释能力确实高于没有融入个人财富数据的PT 价值函数。如表6所示。

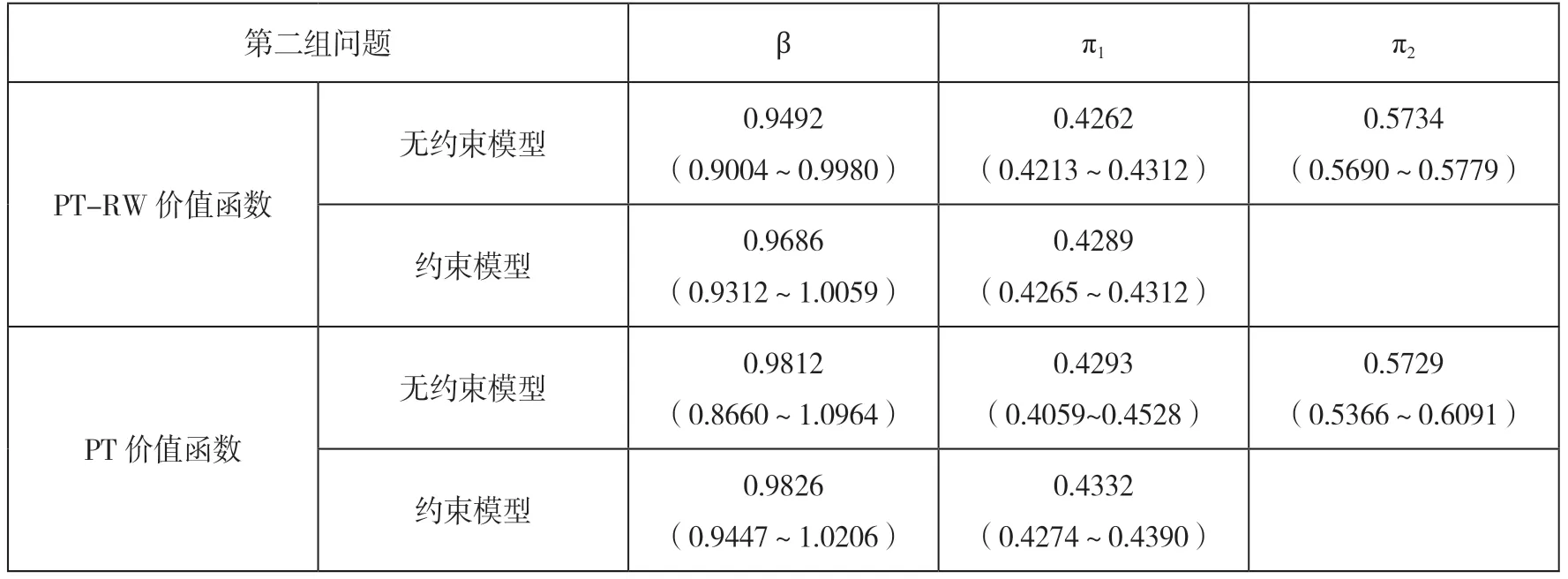
表5 负回报风险资产问题的NLS 参数估计

表6 两个理论价值函数模型的解释力比较

六、结语

虽然实验条件简单，但本次实验仍然取得了许多积极的成果，原因主要有两点：一是相对于经典文献的实验，本次实验所获得的样本量更大；二是放弃对权重函数的全局估计而专注于对价值函数的比较。其中最为主要的成果是PT-RW 价值函数相对PT 价值函数对实验数据的解释能力更强，虽然PT-RW 价值函数中减少了一个参数，仅有的两个参数不仅刻画正定义域以及负定义域函数曲线的弯曲程度，还要刻画损失厌恶这一重要的心理现象，但是相对PT 价值函数，PT-RW 价值函数在自变量中融入了个人财富这一影响人类风险态度的重要因素，也许这正是其数据解释力更强的一个关键因素。PT-RW 价值函数支持负定义域效用函数为凹的假说，全局为凹的价值函数和许多传统经典经济理论相融更加容易，并且价值函数在负定义域中的凹性与人类面对负回报风险资产时表现出的风险偏好的特性也不矛盾。综上，本文的研究从实验方法到研究结论，为从行为经济角度更好地理解人类价值选择偏好进行了有益的尝试。