城市轨道交通客流预测算法研究

秦利南,董路熙

(北方工业大学城市道路交通智能控制技术北京市重点实验室，北京 100144)

0 引言

近年来，随着轨道交通规模扩大，轨道交通网络结构日益复杂，乘客数量剧增，轨道交通客流拥堵问题也越来越明显.准确地把握轨道客流变化特性和不同区间的客流分布状态是开展运营管理的基础，研究快速有效的轨道客流预测算法，对于制定合理的轨道交通运营策略和缓解交通拥堵具有重要的意义.

近几年，在轨道交通客流预测算法研究方面，邹巍等[1]基于轨道交通短时间内客流随机性较强的特点，设计了一种基于改进遗传算法和小波神经网络的短时客流预测方法.刘岩等[2]基于卡尔曼滤波方法构造对应断面列车客流短时预测模型，并用实际例子验证了该预测模型的有效性.徐永实等[3]以城市轨道交通路线中客流量的实时分布为基础，采用数学本质研究进站客流的变化情况，构建了站台客流量与列车车内客流量的实时交互模型；杨静等[4]针对客流的波动性分布特性，提出了小波ARMA组合预测模型；李洁等[5]基于广珠城际铁路的客流变化特征，构建了SARIMA客流预测模型，并用实际客流数据进行了模型有效性验证；Bai等[6]基于ARIMA模型，提出适用于假日的回归分析组合客流预测算法；Roos等[7]基于动态贝叶斯网络，提出了一种基于时空邻域的客流预测方法，并用来预测巴黎城市轨道交通短期客流；Yang等[8]提出了一种基于长短期记忆(ELF-LSTM)神经网络的改进模型，增强了嵌入在客流数据中的长时间相关性特征，并结合了短期特征来预测未来1 h始发地客流.

综上所述，国内外研究人员在轨道交通客流预测方面已取得了较多的成果.在轨道交通客流预测过程中，当客流出现随机波动较大时，传统模型的预测精度经常会受到较大的影响.基于此，本文在采用变点算法对客流数据构成的时间序列处理的基础上，进一步应用小波变化对变点集进行去噪处理，最后利用ARMA-RBF算法对城市轨道客流进行了预测.

1 轨道交通客流预测算法

1.1 变点算法

轨道交通的进出站客流数据具有一定的随机性，客流数据往往呈现出连续变化的锯齿形，直接用原始数据预测时，一些转折点可能会被忽视，进而影响预测精度.变点算法可通过观察函数值在某一时间点发生的质变，根据这些质变点将时间序列分成不同特性的时间段，从而提高了模型的拟合精度.

变点算法的思想是将时间序列进行划分：如果第1个右斜率不为零的点为正，则是峰曲线；如果第1个右斜率不为零的点为负，则是谷曲线，观察右斜率序列中正负号的变化来确定波峰和波谷.经过计算波的平均值与方差以及观察函数，在客流时间序列中进行变点搜索.将变点集用{b(w)}表示，利用变点算法可获取时间序列中的{b(w)}.

对整体序列中均值和方差的计算如式(1)(2)所示：

(1)

(2)

凸(凹)波中均值和方差的计算式如(3)(4)所示：

(3)

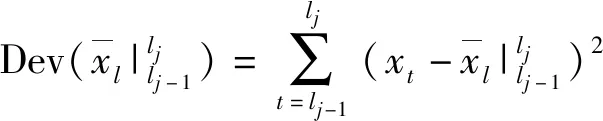
(4)

式中{lj}为峰曲线上的谷点(或谷曲线的峰点).

变点算法搜索变点具体步骤如下.

步骤1将客流数据绘制成曲线；

步骤2设最小变点的观察函数值为控制参数，观察函数如下：

(5)

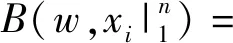
(6)

式中{b(w)}为曲线上的J个变点集，且b(0)=xl1=x1.

步骤3若搜索点的观察函数值大于控制参数时，该搜索点保留；

步骤4观察函数值小于控制参数，该点不是真实变点，则转到步骤3；

步骤5若w=j完成搜索，算法结束.

1.2 小波去噪

轨道交通进出站客流数据在经变点算法处理后，得到变点集，其中有部分变点数据属于噪声干扰，假如用这些数据建立客流预测模型，会影响预测结果的准确性.因此，本文基于小波变化[9]对数据进行二次处理，保证数据的有效性.

小波变化具有多分辨分析的特点，能聚焦到客流数据的任意细节进行多分辨率的时频域分析，有效地去除客流数据中的噪声.小波变化如式(7)所示：

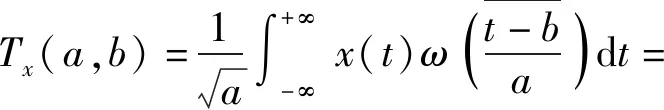
(7)

式中：a为尺度；b为平移量；x(t)为客流数据；ω(t)为基本小波；ωa,b(t)为基本小波的一族函数.

小波函数的频率由a确定，时段由b确定，a与b由具体小波基函数确定，不必标定.具体步骤为：

步骤1输入原始客流数据；

步骤2小波变换多尺度分解，小波基函数主要有haar小波、db小波、sym小波、coif小波4种；

步骤3各尺度小波系数去噪，用不同层数进行处理；

步骤4分别计算信噪比，并进行结果对比，选择小波基函数，输出最后的客流数据.

1.3 组合预测算法

1.3.1 ARMA算法

ARMA算法(自回归滑动平均算法)[10]是研究客流时间序列曲线的重要方法，适用于处理平稳的时间序列曲线，由AR算法(自回归模型算法)与MA算法(移动平均算法)“混合”构成.

假设时间序列yt满足：

yt=θ0+θ1yt-1+θ2yt-2+…+θpyt-p+εt+
η1εt-1+η2εt-2+…+ηqεt-q

(8)

则称时间序列yt服从(p,q)阶ARMA算法.

式中：θi为自回归系数；p为自回归算法的阶数；εt为零均值白噪声序列；ηi为q阶移动平均算法的系数.

1.3.2 RBF神经网络算法

RBF神经网络(Radial Basis Function)又称径向基神经网络[11]，属于前馈网络，有结构简单、学习速度快、在非线性数据处理中映射能力强等特点；RBF神经网络属于3层神经网络：输入层、隐层和输出层；各层之间的变换关系不同：从输入层到隐层的变换是非线性的，而从隐层到输出层变换是线性的.流程图见图1.

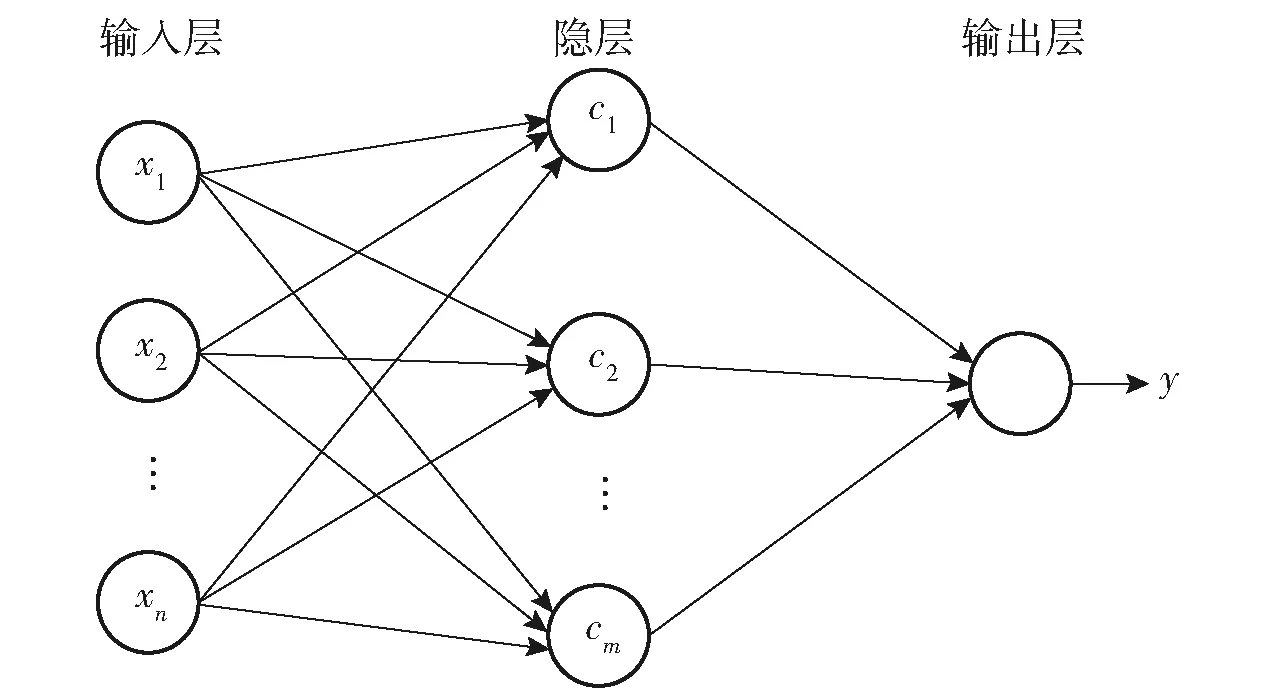
图1 RBF神经网络流程图

假设输入层有n个客流数据输入，隐层有m个计算节点，则对于每1个输入信号，隐层会产生1个m维空间向量，这向量由径向基函数组成；ω是隐层与输出层连接的系数，最后输出y，为单输出，见式(9)：

(9)

式中：σ为径向基函数宽度；ci为径向基函数中心.

1.3.3 ARMA-RBF组合预测算法

经变点算法、小波去噪处理后的城市地铁客流数据属于非平稳时间序列，通过差分计算将非平稳时间序列转变成平稳时间序列，并用ARMA模型预测，但ARMA模型不能预测客流数据中的非线性.本文构建ARMA-RBF组合客流预测算法，降低模型的预测误差.具体步骤如下.

步骤1输入二次处理后的客流数据.

步骤2检验平稳性，计算自相关函数与偏自相关函数的值并绘制图形，若图形具有拖尾性，则属于平稳时间序列，转到步骤4；若图形无拖尾性，则属于非平稳时间序列，转到步骤3.

步骤3差分计算，将非平稳时间序列转变成平稳时间序列.

步骤4假设客流时间序列yt由线性Lt和非线性Nt构成，即：

yt=Lt+Nt

(10)

步骤5确定p、q，利用AIC准则确定ARMA算法的阶数.

步骤6针对地铁客流时间序列中的线性部分，采用ARMA模型进行客流预测，预测结果为t，令具有非线性特征的预测误差为et：

et=yt-t

(11)

步骤7将et随机分成2部分：75%的误差作为训练集，25%作为测试集.

步骤8利用K-means聚类确定径向基函数中心，用平均法确定径向基函数宽度，从而确定RBF算法.

步骤9采用训练集对RBF算法训练后，用RBF对测试集的结果进行预测.

步骤10令RBF的预测值为t，则预测结果如下：

t=t+t

(12)

2 案例分析

为预测地铁客流数据的变化情况，采集北京地铁4号线新街口、平安里与西四地铁站连续2周06:00—22:00的进出站客流数据，以5 min为间隔统计数据，同一天内新街口、平安里与西四地铁站的进站客流数据及出站客流数据统计见图2.

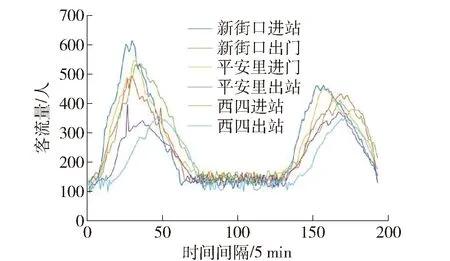
图2 进出站客流数据

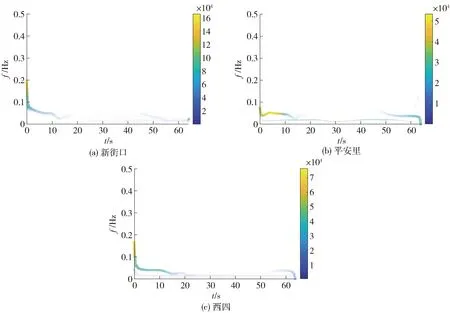
图3 变点算法

选取同一天3个车站的进站客流数据为例进行研究.基于变点算法对进出站客流数据进行预处理，得到的变点集根据状态不同分为4个模式区间，分别为08:15—10：00，10：00—16：40，16：40—19：40，19：40—次日08:15，体现了正常的早晚高峰时间阶段，验证了变点算法的可信度(图3).

经过变点算法处理之后，基于小波变化对数据进行去噪处理，分别用haar小波、db小波、sym小波、coif小波4种对数据去噪，并在这些小波变化的基础上进行多层数分解处理.

用haar小波去噪，如图4所示.

用db小波去噪，并进行多层分解，如图5所示.

用sym小波去噪，并进行多层分解，如图6所示.

用coif小波去噪，并进行多层分解，如图7所示.

对4种小波函数及不同分解层数下的小波变化，分别计算信噪比，结果见表1、表2.

SNR=10×lg(powersignal/powernoise)

(13)

信噪比越大，去噪效果越好.在db小波函数分解层数为4时，信噪比最大.因此，本文采用小波基函数db4对原始客流数据进行去噪处理.

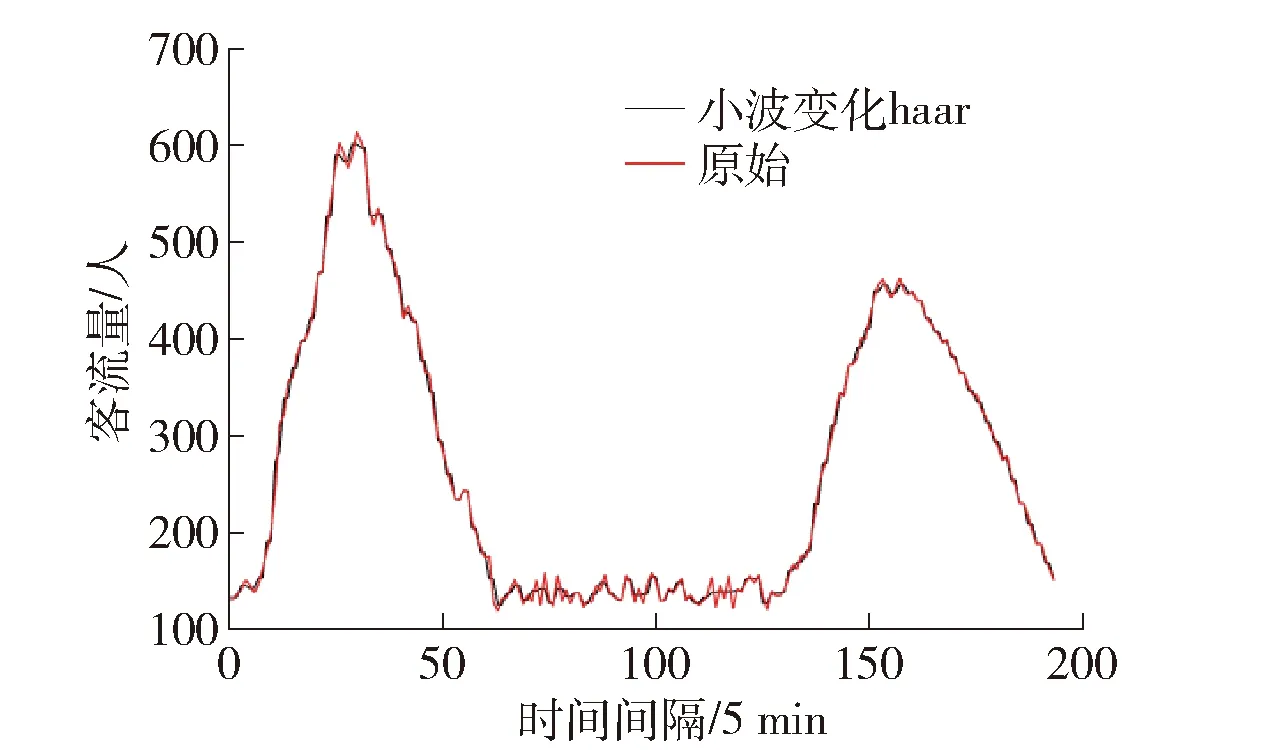
图4 haar小波变化

经变点算法、小波去噪处理后，检验时间序列的平稳性，分别计算自相关函数值与偏自相关函数值并绘制图8.

通过图8可明显看出，自相关函数从1.0下降至0.0并在邻近波动，且波动幅度逐渐减小；偏自相关函数从1.0衰减到0.0后，并在邻近震荡，且无限向0.0靠近；两者都具有拖尾性，属于平稳时间序列，满足ARMA算法的适用条件，因此可用ARMA算法对客流进行预测.

图5 db小波变化

图6 sym小波变化

图7 coif小波变化

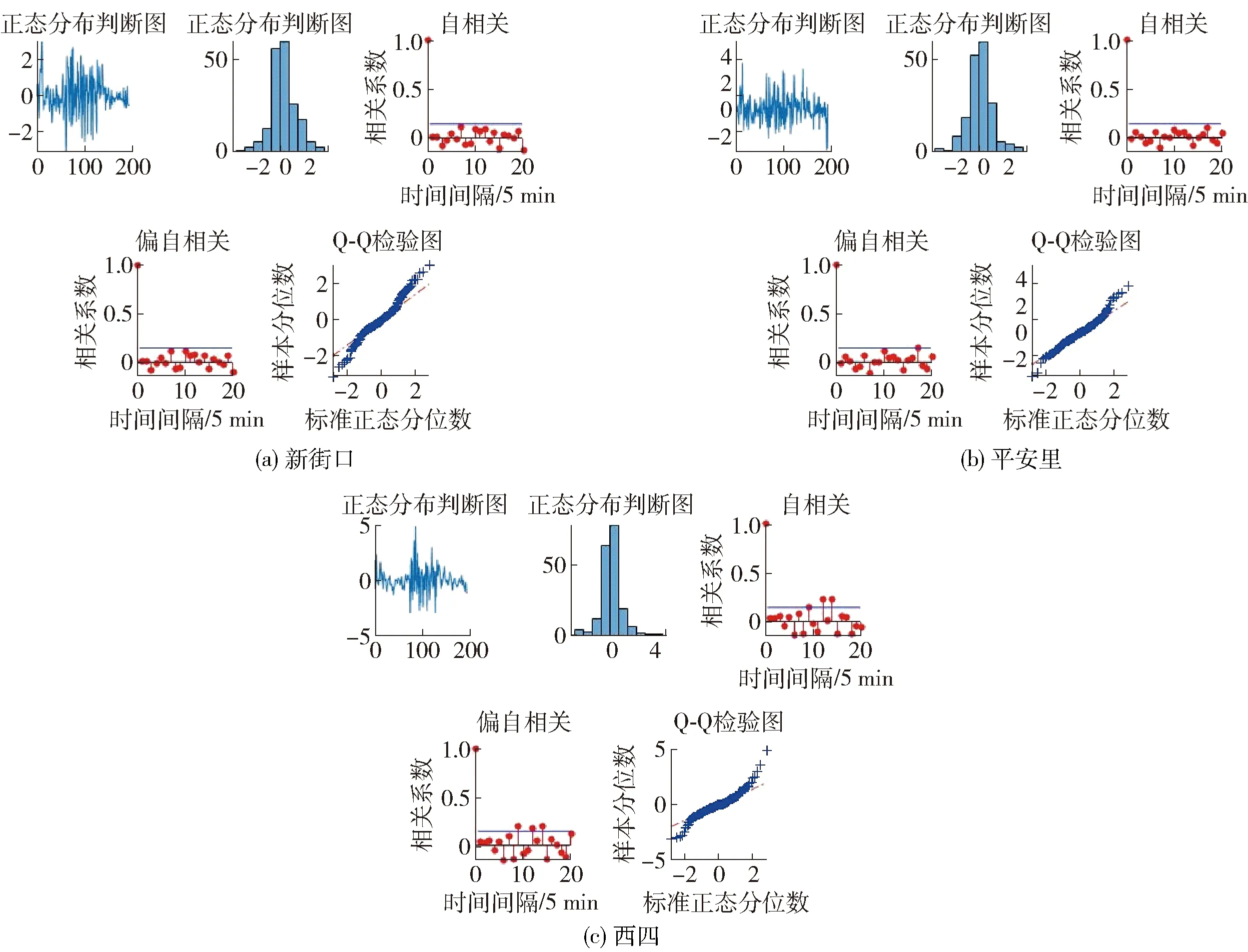
图8 平稳性检验图

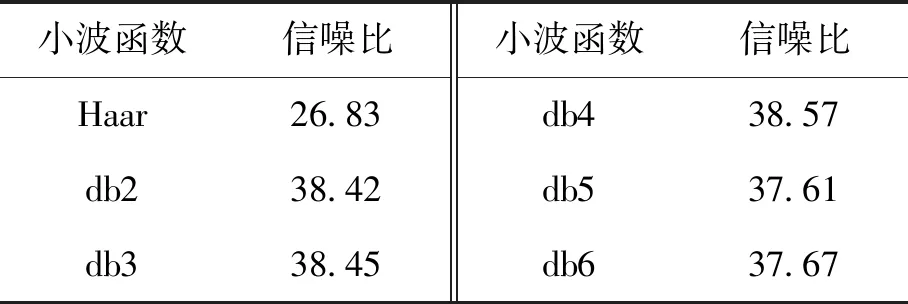
表1 信噪比对比一

表2 信噪比对比二

基于AIC准则对ARMA模型的阶数进行确定.

通过实验计算，当p=2，q=3时，AIC取得最小值，因此ARMA算法的阶数确定为ARMA(2，3).

用ARMA-RBF、ARMA、RBF 3种算法对进出站客流数据进行预测(图9)，分别计算绝对百分比误差并进行比较(表3～表5).

绝对百分比预测误差占比统计如下：

经计算得出，在<10%的误差范围内，ARMA-RBF组合预测算法的平均绝对百分比预测误差为93.9%、RBF算法为59.37%和ARMA算法为73.9%.

由表3～表5可知，ARMA-RBF组合预测算法的预测误差最小，RBF算法的预测误差最大，ARMA算法的预测误差介于两者之间.结果表明，ARMA-RBF算法的预测结果比较理想，优于单一模型的预测效果.因此，可用于提高城市轨道交通系统进出站客流的预测精度.

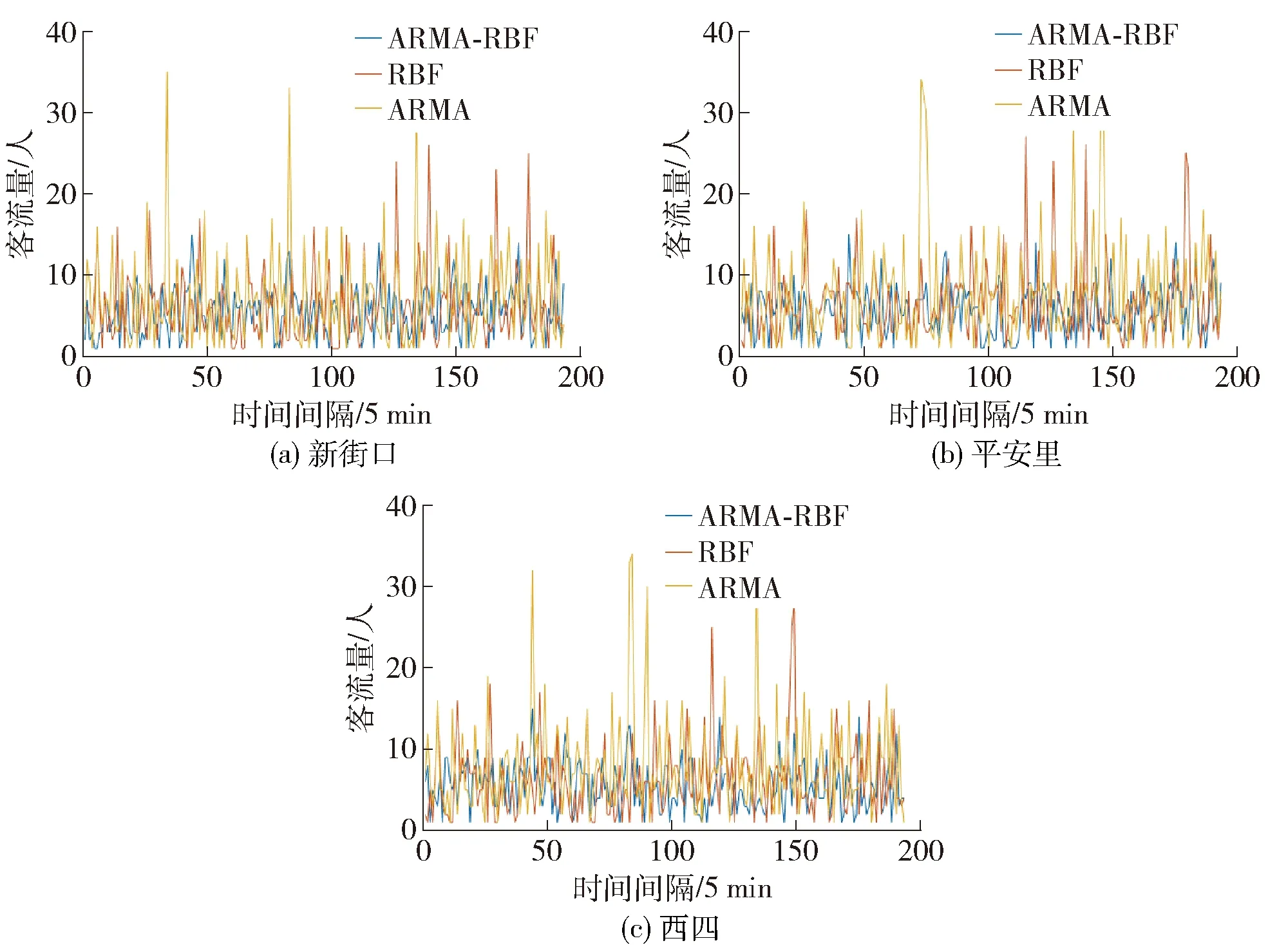
图9 MAPE值对比

表3 新街口MAPE值对比表 %

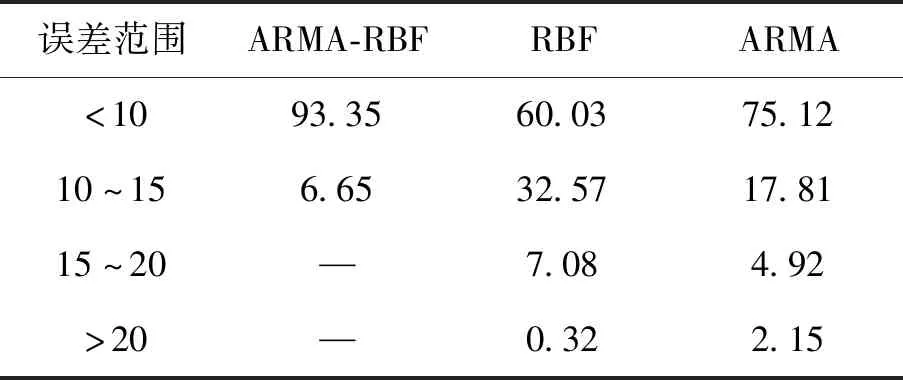
表4 平安里MAPE值对比表 %

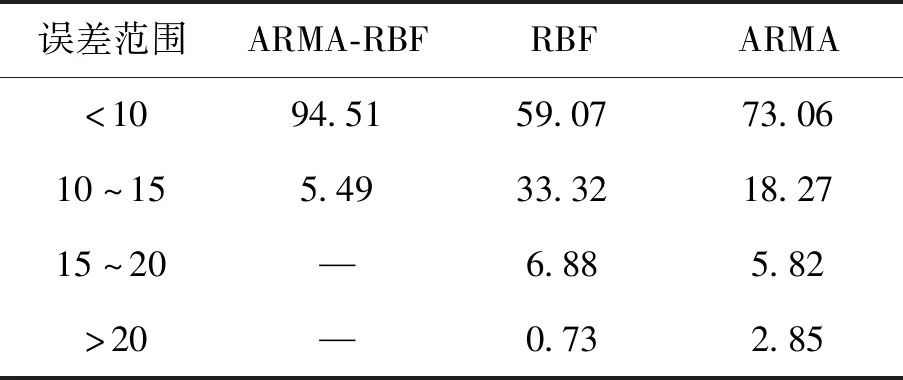
表5 西四MAPE值对比表

3 结论

为了使城市轨道交通客流能有效进行预测，针对非线性部分，本文用变点算法在客流时间序列中寻找变点，并基于小波变化对变点集进行去噪处理，提高数据的有效性，在此基础上基于ARMA模型和RBF神经网络算法，构建了ARMA-RBF客流预测算法.以实际客流数据进行验证，结果表明，在误差范围小于10%时，ARMA-RBF算法预测平均精度为93.9%，分别比ARMA模型和RBF模型高31.95%、36.77%，表明了本文所提方法的有效性，对轨道交通客流预测具有一定的参考意义.