基于密度控制的公交线网布局结构优化算法研究

仝 炜

(昆山市轨道交通投资发展有限公司，昆山 215332)

公共交通在交通系统中的作用越来越大，特别是公交系统的发展势头十分惊人，但由于布局结构的不合理，使公交系统的利用率下降，加重了交通拥堵问题的严重程度[1].因此必须对公交线网的布局结构进行优化，才能发挥公交系统自身的优势，实现公交系统的长期可持续发展.优化过程中重点是如何从应用角度与理论方面实现公交系统的有效协作与衔接，成为发展的焦点.而通过公交线网布局结构优化算法则可顺利解决该问题[2].公交线网布局结构优化算法能对公交线网实施布局结构上的大规模优化，有利于高效发展公共交通.现阶段，针对公交线网布局结构优化算法的研究，国内外的研究成果呈现出多样化的特点.国外目前主要基于系统工程学与运筹学进行公交线网布局结构优化算法的研究；而我国的研究起步较晚，目前主要引入灰色方法、模糊方法、人工智能等进行公交线网布局结构优化算法的研究[3].为进一步改进公交线网布局，本文提出一种基于密度控制的公交线网布局结构优化算法.

1 基于密度控制的公交线网布局结构优化算法

1.1 设置公交站点

采用密度控制方法对公交站点的布设密度进行控制，根据公交吸引带的密度分布设置公交站点，包括设置首末站、起讫点以及中途站点[4-5].其中公交吸引带的密度分布如图1所示.

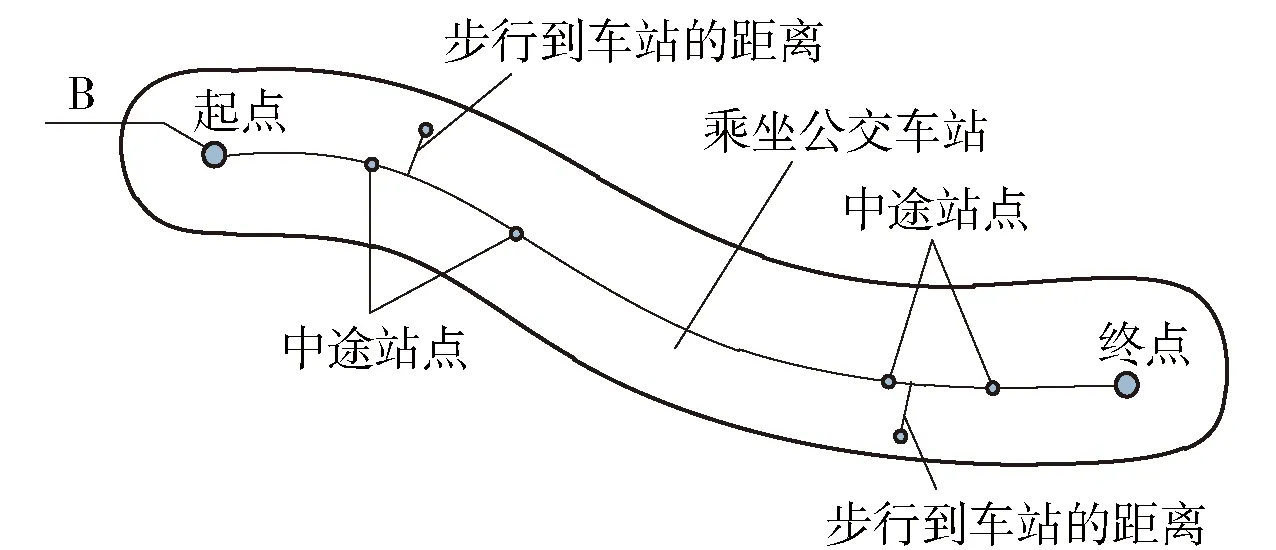
图1 公交吸引带的密度分布

1.1.1 设置首末站

根据公交吸引带的密度分布特点，按照布设原则设置首末站，设置方法如下.

1) 与道路网的建设和发展相协调：与道路客流同向布设，紧靠道路客流集散点.

2) 留出服务范围：选择布设在体育中心、文化中心、码头、公园、火车站、居住区等位置，留出约300 m的服务半径.

3) 站点规模的确定需要根据运营车辆的配置来决定：大型站点的容量为50辆以上；中型站点的容量为26～50辆；小型站点的容量低于26辆.

4) 出入口设置于道路上：需要保证该道路服务水平较好、具备富余的使用面积.

1.1.2 设置起讫点与中途站

在交通高峰期，当交通区的总吸引量或总发生量大于设站标准的时候，需要在该区域设置起讫点，设置与否的判断标准为其中途站点的实际运载能力[6].具体设置方法为：首先计算中途站点实际运载能力如式(1)所示：

(1)

式中：C0为中途站点的实际运载能力，具体为每高峰小时乘客的总量；B为中途站点的平均乘客数；TH为高峰小时各个车辆之间的发车间隔.

则交通小区所对应的中间站点的实际运载能力见式(2)：

C(i)=C0×N(i)

(2)

式中：C(i)为交通小区i的中间站点的实际运载能力；N(i)为交通小区i中间站点的实际总个数，根据交通小区的实际出行量与公交线网的具体密度可得出该数值[7].

当交通小区所对应的中间站点的实际运载能力小于该交通小区的总吸引量或总发生量，则在该交通小区设置起讫点.在全局规划中，交通小区起讫点的分布并不均匀，需要结合交通小区布设线路的情况、实际面积大小、实际性质以及出行量来决定[8].在未确定公交线路时，交通小区起讫点数量设置分以下3种情况进行.

1)根据出行量的大小对起讫点进行设置：

(3)

式中：F(i)为交通小区起讫点的设置数量；T(i)为交通小区i公交乘客总吸引量或总发生量；N0为所设置的站点总数，见式(4)；T为全局规划区公交乘客总吸引量或总发生量，见式(5)所示.

(4)

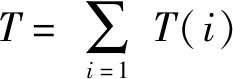
(5)

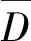
2) 根据区域密度及面积对起讫点进行设置：

(6)

式中：ρ(i)为i这一交通小区的实际路网密度，通常位于市中心时选取4～5 km/km2,位于近郊地区时选取2～3 km/km2,位于一般地区时选取3～4 km/km2；S(i)为i交通小区的实际面积；D(i)为i交通小区的运距平均值，通常位于市中心时选取0.4～0.5 km，位于近郊地区时选取0.6～0.8 km，位于一般地区时选取0.5～0.6 km[9].

3)根据实际要求对起讫点进行设置，通常这些地区为特殊地区，如居民小区、码头、风景区等：

(7)

式中：R为额定公交车载客数，其中单节车是72人，铰接车是129人；r为高峰小时实际满载率，通常取值为0.85；ti为实际发车间隔；k0为终点与起点断面流量的比值，通常取值为1.5～2.0[10].

根据公交吸引带的密度分布设置中途站，对中途站进行密度控制，其设置需要对中途站之间的间距进行研究，设置的最优中途站间距应满足使全部乘客获得最短总出行时间.

1.2 布设公交线路

以设置的公交站点为基础，通过对公交线路功能进行分析，即对公交线路进行定性与定量分析，对布设原则进行明确，实现对公交线路的层次化布设[11].布设的公交线路包括3个层次，分别为公交支线、公交次干线以及公交干线，如图2所示.

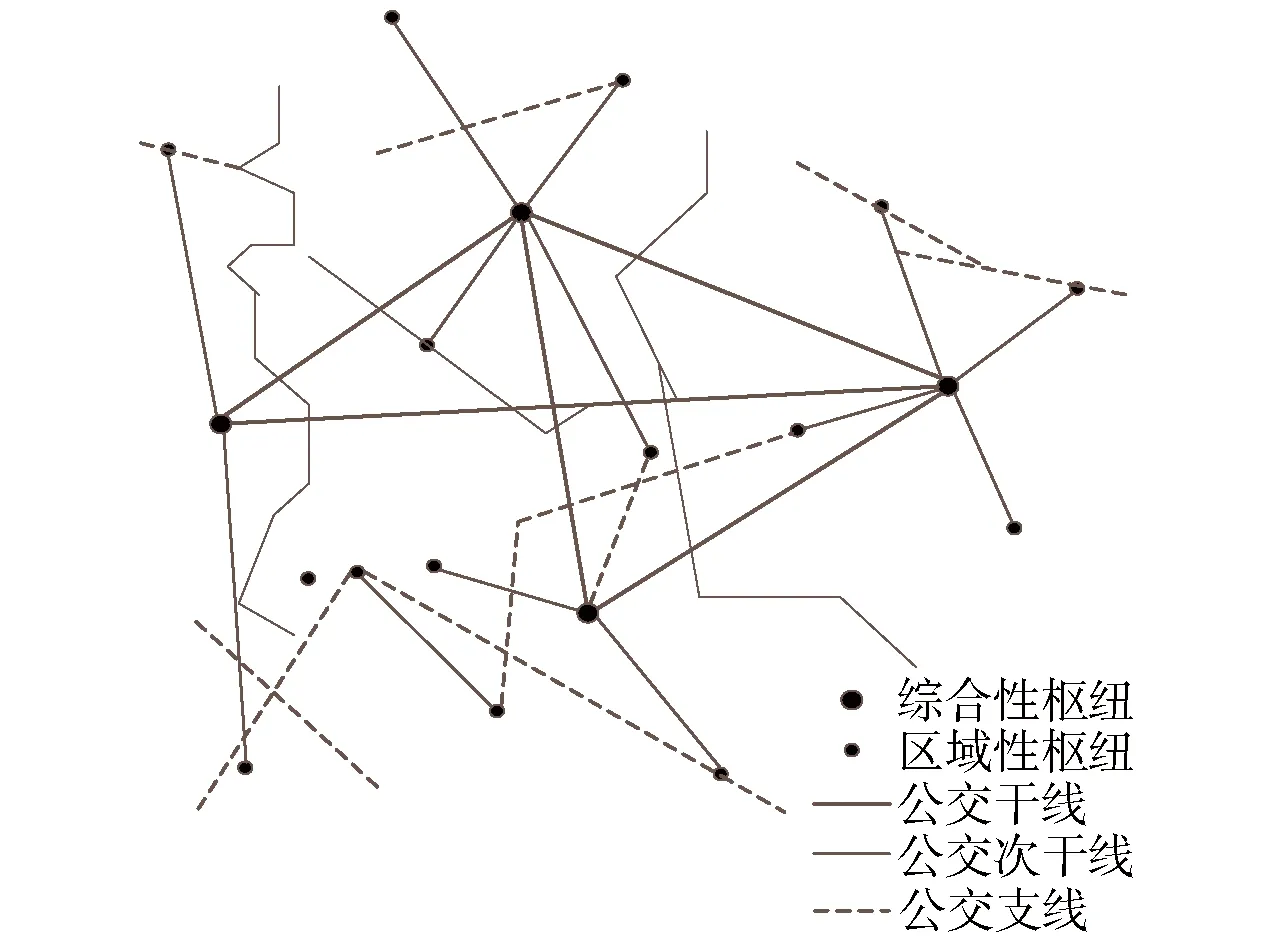
图2 布设的公交线路具体示意图

对公交线路功能层次进行分析，首先需要划分公交干线层[12]；然后对公交次干线层进行划分；最后划分公交支线层.在划分公交干线层时，需要分析道路网布局与客流，并根据区域功能特点划分交通大区，将交通大区作为基础，以公交综合枢纽的选址方法为依据，对公交综合枢纽进行确定.同时，通过公交综合枢纽、道路网实际结构特点以及客流走廊的实际走向，确定公交干线层结构基本形式，分析公交线网中的线路，选取符合条件的线路作为备选公交线路.对公交干线进行筛选，将其作为公交干线备选集.在划分公交次干线层时，要通过交通区域划分确定区域公交枢纽，通过公交线网现状分析与筛选确定公交次干线备选集.在划分公交支线层时，根据区内辐射式发散的公交线路特点实现公交支线层的独立划分.

1.3 实现公交线网布局结构优化

根据设置的公交站点与布设的公交线路，利用密度控制方法实现公交线网布局结构优化[13].在公交线网布局设计时，如果只考虑公交线路长度的布局会造成交通拥堵的结果，导致布局后续阶段很难进行布线.因此，需要考虑密度问题，以实现公交线路密度与站点密度能满足乘客对密度的最低覆盖度要求为目的，对目标区域内的各层密度进行分析.

构建最大服务客流密度模型，将目标区域划分成具有多层圆环的圆形整体，在该区域内公交线路呈现辐射型分布的状态，建立公交线网最优布局序列.在最优布局序列中将公交站点密度与布设线路密度当作基本信息单位，见式(8)：

(8)

式中：OD为客流密度；i、j表示路径；qi为2条路径之间的实际轨迹强度；qj为最优路径迭代代价函数；m为圆环数量；sk为初始出发点；xk为终点；μij为满足路径优化的最低客流密度，见式(9)：

(9)

式中：h、g表示最内层圆环中的公交线路密度和最外层圆环中的公交线路密度；V为圆环中心位置；l为最内层圆环到最外层圆环的客流密度，见式(10)：

(10)

结合式(8)、式(9)构建目标函数值，并求取最优解：

(11)

式中dij为客流直达路径.

为保证得出最优的线路，需要通过适当的约束条件约束目标函数：

(12)

根据上述分析得出公交线网布局结构优化的具体步骤如下.

1) 初始化：输入实际情况的相关参数，确定优化目标与客流密度OD；

2) 确定起终点站，计算其乘客直达量；

3) 初始化公交线路，使布设的主干线网公交线路的数量为1；

4) 对i、j这2条路径之间的实际轨迹强度、最优路径的迭代代价函数等参数实施初始化；

5) 计算满足路径优化的最低客流密度，并以此为基础计算最内层圆环到最外层圆环的客流密度[14]；

6) 根据客流密度构建目标函数值，并对目标函数值对应的最优值进行记录；

7) 对轨迹强度进行修改，更新信息；

8) 对于路径i、j，令最优路径的迭代代价函数等于0；

9) 判断公交线路密度与站点密度能否满足乘客对密度最低覆盖度要求的约束条件；

10) 如果不满足约束条件，对其终点进行回溯，并计算满足该约束条件的实际直达乘客量；

11) 当满足该约束的路径是主干线路，重复以上步骤，直到获取满足该约束条件的N条主干线路，若不是主干线路，则修正后重复以上步骤，直到获取满足该约束条件的N条主干线路；

12) 更新客流密度OD，删除已布设主干线路的实际直达乘客量，当客流量仍符合约束条件，则结束优化过程.

根据上述步骤，通过公交线路密度、公交站点密度以及客流密度控制的基础上，实现公交线网布局结构优化[15].

2 实验测试

2.1 实验设置

对设计的基于密度控制的公交线网布局结构优化算法进行实验测试.构建1个公交路网结构图，如图3所示.对该路网进行划分，并将其划分为9个交通区，其编号分别为A～I.在其中选择35个主要站点，对其进行编号，为1～35号.

图3 城市路网具体结构示意图

该公交线网优化之前的公交线路走向如表1所示.

表1 公交线网优化之前的公交线路走向

利用设计的基于密度控制的公交线网布局结构优化算法对公交路网进行公交线网布局结构优化，通过C++语言对该算法进行实现，并通过MATLAB软件进行数据处理，以优化公交路网的公交支线、公交次干线以及公交干线.在优化过程中获取不同循环次数下优化后公交路网布局结构中线路重复系数.

2.2 实验结果与分析

在循环次数为50次以上和50次以下时，优化前后公交路网布局结构的线路重复系数具体如图4所示.

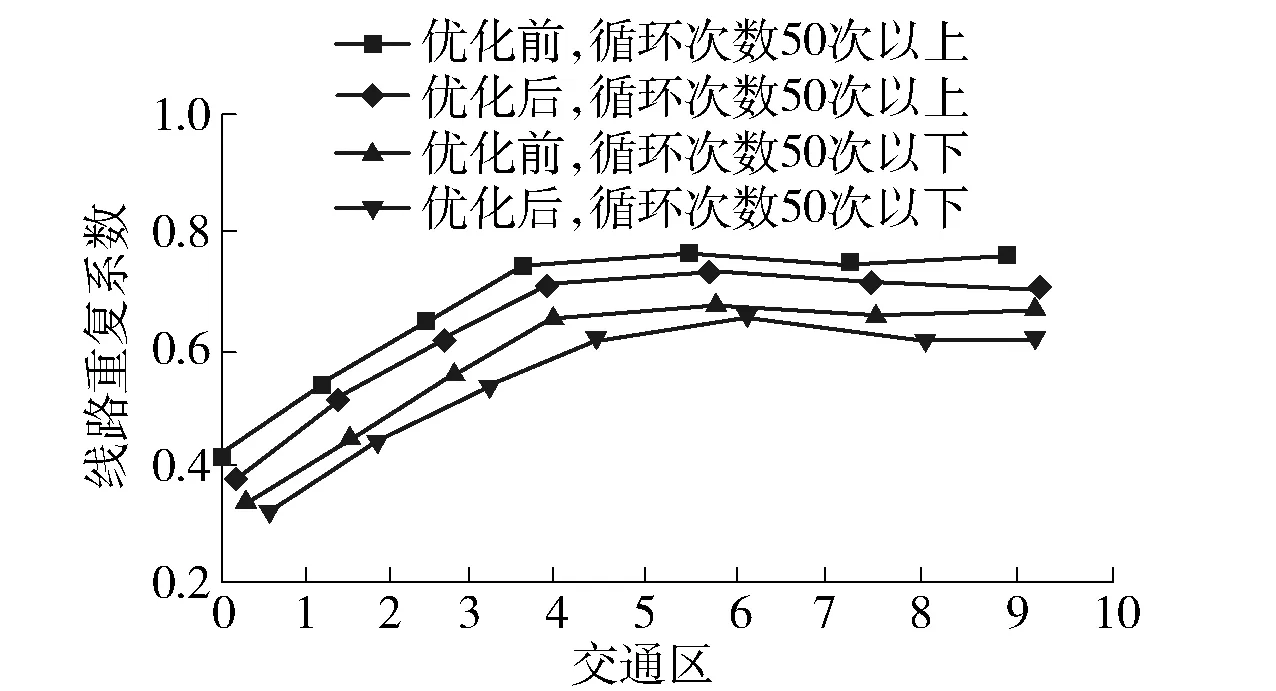
图4 优化后的线路重复系数数据

从图4中可明显看出，当循环次数为50次以上时，经所提算法优化后的线路重复系数低于优化前的重复系数；当循环次数为50次以下时，优化后公交路网布局结构的线路重复系数低于优化前的重复系数.并且当循环系数为50次以上和50次以下时，优化后的最低重复系数分别为0.37、0.30，重复系数较低，能满足交通量对线路的实际需求.这是由于所提算法采用的是分层划分方法，分别对首末站、起讫点以及中途站点进行设置，解决了以往全局式规划后线路分布不均匀的问题.

为了验证所提算法的应用性能，将最优路径作为衡量线路规划算法的指标，得出的结果如图5所示.

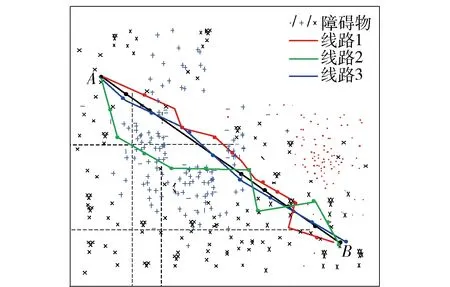
图5 路径规划结果

分析图5可知，A为起点，B为终点，图中得出了3条线路，其中线路2长度较长，经济性较差，线路1虽然长度低于线路2，但是存在不能有效躲避障碍物的问题.相比较之下，线路3为经所提算法优化后得出的线路，既具有较短的长度，又能有效躲避障碍，说明该线路具备有效性与经济性，可选取该线路作为最优路径.根据上述分析可知，所提算法优化后的线路效果最佳.

为了验证所提算法的优势性，进一步以公交行驶路径长短作为经济性衡量指标，对基于灰色方法、基于模糊方法的公交线网布局结构优化方法与所提算法进行对比，结果如图6所示.

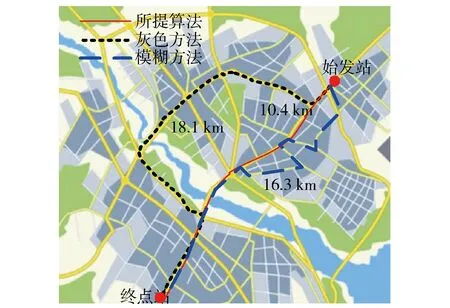
图6 不同方法规划下路径长短对比结果

分析图6可知，采用所提算法、灰色方法和模糊方法设计的公交线网布局结构进行行驶，实际路径长度分别为10.4、18.1、16.3 km，其中，所提算法的公交行驶路径最短，既具有行驶时间较短的优势，又具有燃油损耗较低的优势，说明该算法的经济性较强.这是由于该算法利用蚁群算法能对公交线网进行有效规划，从而获取最优路径.

3 结束语

为了优化公交线网布局，提出基于密度控制的公交线网布局结构优化算法.实验结果表明该算法实现了循环次数变化下线路重复系数的降低，并且能获取最优路径，与现有方法相比，在经济性方面具有明显的优势.但该算法在目标函数值的计算部分仍然存在一定改进空间，日后将针对该部分进行深入细致的研究.