素养导向 深度理解——安徽中考数学选择压轴题赏析及教学启示

江苏省常州市武进区前黄实验学校(213172) 徐 宏

《义务教育数学课程标准(2011年版)》指出:“评价应以课程目标和课程内容为依据, 体现数学课程的基本理念,全面评价学生在知识技能、数学思考、问题解决和情感态度等方面的表现.”最值问题是中考数学中常常出现的热门题目,近几年安徽中考数学选择压轴题都是求最值问题的题目,试题设计别具匠心,很好地体现了课程标准的精神,以素养为导向,考察学生对问题的深度理解.希望通过试题赏析,能全面领会数学课程的基本理念,关注核心内容,引领并促进数学核心素养在平时的教学中落地生根.

1 试题呈现

(2019年第10 题)如图1,在正方形ABCD中,点E,F将对角线AC三等分, 且AC= 12, 点P在正方形的边上,则满足PE+PF=9 的点P的个数是( )

A.0 B.4 C.6 D.8

图1

图2

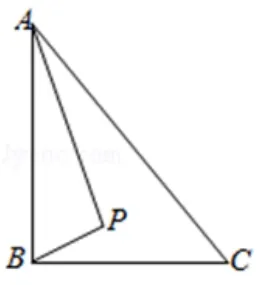
图3

(2017年第10 题)如图2, 在矩形ABCD中,AB= 5,AD= 3, 动点P满足则点P到A、B两点距离之和PA+PB的最小值为( )

(2016年第10 题) 如图3, Rt∆ABC中,AB ⊥ BC,AB= 6,BC= 4,P是∆ABC内部的一个动点, 且满足∠PAB=∠PBC,则线段CP长的最小值为( )

2 试题解答

(2019年第10 题) 解答: 如图4, 作点F关于BC的对称点M, 连接CM, 连接EM交BC于点N, ∵点E,F将对 角线AC三 等分, 且AC= 12, ∴CE= 8,CF= 4,∵点M与点F关于BC对称,∴CF=CM= 4,∠ACB= ∠BCM= 45°, ∴∠ACM= 90°, ∴EM=则在线段BC存在点N到点E和点F的距离之和最小为∴在线段BC上点N的左右两边各有一个点P使PE+PF= 9,同理在线段AB,AD,CD上都存在两个点使PE+PF=9.即共有8 个点P满足PE+PF=9,故选: D.

图4

图5

图6

(2017年第10 题)解答: 设∆ABC中AB边上的高是∴动点P在与AB平行且与AB的距离是2 的直线l上,如图5,作A关于直线l的对称点E,连接AE,连接BE,则BE就是所求的最短距离.在Rt∆ABE中,∵AB= 5,AE= 2+2 = 4,∴BE=即PA+PB的最小值为故选D.

(2016年第10 题) 解答: ∵∠ABC= 90°, ∴∠ABP+∠PBC= 90°, ∵∠PAB= ∠PBC, ∴∠PAB+ ∠ABP=90°, ∴∠APB= 90°, ∴点P在以AB为直径的⊙O上,连接OC交⊙O于点P, 此时PC最小.在Rt∆BCO中,∵∠OBC= 90°,BC= 4,OB= 3, ∴OC= 5, ∴PC=OC −OP=2.∴PC最小值为2.故选B.

3 试题赏析

3.1 简约亲切,彰显人文关怀

这几个小题从表述上看,给人以简洁明了之感,减轻了学生阅读的负担;图文结合,文字简练,表述清晰,极具简约美.作为选择压轴题,选取的考察知识点是常见、常考的“点圆最值”、“将军饮马”模型,亲切的背景缓解了中考带来的紧张不安,从心理上给考生树立了信心,为考生理解题意、解决问题提供了方便,有助于考生自我潜能的挖掘,也彰显了命题组老师对考生的人文关怀.

3.2 构思精巧,凸显核心素养

虽然这几个小题考察知识点是常见、常考的“点圆最值”、“将军饮马”模型,但不是简单的套用模型去考察学生的计算能力.如2019年山东某市中考数学选择压轴,只是将背景放入平面直角坐标系,再将一些条件复杂化而已.

如图7, Rt∆ABO中, ∠OBA=90°,A(4,4), 点C在 边AB上, 且点D为OB的中点, 点P为边OA上的动点,当点P在OA上移动时,使四边形PDBC周长最小的点P的坐标为( )

图7

安徽中考数学这几个选择压轴题从构思上看,设计精巧,新颖巧妙,凸显核心素养.学生面对这几个试题时,“似曾相识”却又“耳目一新”, 有“跳一跳, 够得到”的冲动.如2017年第10 题,学生看到要求解的“距离之和PA+PB的最小值”,很容易想到“将军饮马”模型,但是那条直线在哪里呢?命题组老师巧妙的利用面积、利用平行线之间距离将直线“隐藏”了.如同: 平面直角坐标系中,已知点A(a,a),实际就是点A是直线y=x上的动点.再如2019年第10 题,此题源于“将军饮马”模型而又不落俗套,从封闭的“将军饮马”求最值问题转化为开放的判断点的个数问题.由模型求出最小值不是难事,但是要确定符合条件的点有几个,则凸显了学生的数学素养.考察学生直观想象、逻辑推理、数学运算等核心素养和关键能力.学生首先通过直观感觉对称性,逻辑推理出点P的个数只可能是0 个、4 个或8 个.看到“满足PE+PF=9”,也很容易想到“将军饮马”模型去求最小值,从而通过比较这两个的大小来解决问题.

3.3 变中究质,追求深度理解

这几个选择压轴题让学生感觉到既熟悉又新鲜,能显示出“稳”中不失“变”的立意,立足于学生对初中几何知识的深刻理解,角度新颖,学生想要做出试题,就要能对问题的本质做到深度理解.如2017年第10 题,不仅考察“将军饮马”模型,更考察点的轨迹问题,体现了初高中的知识衔接.2016年第10 题同样也考察点的轨迹问题,需要对定理“直径所对的圆周角是直角”做到深度理解,反之应用,需要动手与动脑相结合.2019年第10 题更是巧妙地将正方形、等腰三角形、轴对称、勾股定理、三角形的三边关系等知识串联起来,体现了形与数、动与静之间的联系,在常规背景中考察学生对于问题本质的深度理解.

文[3]指出: 有些地方的数学中考人为地编造“难题”,显得很不自然,求解过程让人很难想到,难以体现数学的学科特点和本质,无法体现解决数学问题的一般规律和通性、通法,绝大多数学生根本想不到解法,得分率非常低,如此“造题”为难学生,考试的意义何在呢? 安徽省近三年求最值问题的题目设计别具匠心,既有区分度,学习优秀的学生也能够上手,起到了考查与选拔的作用.本人也曾在文[4]中详细分析了一个几何最值问题,感觉到有些几何最值试题只是在考技巧,忽略了对数学本质的探究、理解.

4 教学启示

中考试题都是经过命题专家在课标、教材的指引下精心设计的,只有深入其中去思考、去体会、去研究,才会发现其引导功能和教学价值,进而加深对课标和教材的理解,使教师的教学工作游刃有余.

4.1 以教材为根本,关注核心素养

中考试题的是以《义务教育数课程标准(2011年版)》标准命制,以教材为根本,根据初中学生的生理、心理特点等来命制,很多题目的情境或原型都来自教材.如同“点圆最值”、“将军饮马”模型的题目在人教版、苏科版等全国各种版本教材中都可以找到.但是中考试题通常是以教材例习题为“背景”,经过了命题组老师的巧妙构思编拟而成的,它们源于教材,又高于教材.这就启发我们在教学中,要关注课程标准,回归教材,关注基础知识的落实,同时更要关注学生的核心素养.引导学生努力探索问题的“衍生点”;创造性地使用教材,开发丰富有效的课程资源,引导学生进行探究性学习,在例习题及中考题的探究中理解问题本质,在此基础上寻找知识的“生长点”.

4.2 积累活动经验,引导感悟思想

《义务教育数课程标准(2011年版)》把原来的“双基”扩充为“四基”,数学活动经验的积累与数学思想方法被提到了新的高度.如同这几个中考数学选择压轴题对学生思维的深度与广度都有一定的要求.因此,在教学中教师不能以解决问题作为教学的终结点,而应将数学基本活动经验的积累贯穿于教学过程中,要注重直观想象、逻辑推理、数学建模等核心素养的培养,让学生在学好基础知识、掌握基本技能的同时不断积累活动经验,并且能够运用实践,内化为自己的知识经验.同时,数学思想方法更应渗透在数学教学的整个过程之中.教师在教学中要重视对常用数学思想方法的渗透、总结与提炼,要结合典型问题的研讨,多给学生独立思考、自主探索的时间与空间,抓住一题多解、多题一解、一题多变的特点,引导学生不仅要学会知识的应用,更要领悟知识应用中的数学思想方法,形成应用数学思想方法解决问题的自觉意识,提高用思想方法进行数学思考的水平.

4.3 培养思维能力,形成数学素养

《义务教育数学课程标准(2011年版)》提出“数感”“符号意识”“几何直观”“推理能力”“运算能力”等10 个核心词,《普通高中数学课程标准(2017年版)》又提出数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析这六个数学学科核心素养,学生的数学素养是多种能力及意识的综合表现,这要求我们在教学中要通过一个个数学探究、数学实验、数学应用等逐渐培养能力,形成学生的数学素养.具体到解题教学中,教师要专研教材,创设开放性问题,一题多变,一题多解,多解归一,这有助于培养学生思维的深刻性、灵活性、严密性、创造性和批判性.