巧用待定系数法求解一类二元二次函数最值范围

陕西省城固师范学校(723200) 刘敬民

对于“实数x,y满足Ax2+Bxy+Cy2=D(D ̸= 0),求s=ux2+vxy+wy2的取值范围”的问题,在各级各类的数学考试和竞赛中经常出现,而且在各类数学报刊杂志给出了不同的解法.文[1]采用消元替换法,以y=kx为起点,换元后实现双变量的分离,达到消元的效果;文[2]根据x,y的齐次特点,采用整体代换,再通过换元转化为求一元分式函数f(t) =值域问题;文[3]通过配方后用三角换元法处理此类问题;文[4]通过构造直线和圆锥曲线,利用直线和圆锥曲线的位置关系来解决问题,真可谓百花齐放,百家争鸣.

本文利用待定系数法并借助于一个完全平方式的非负性,自然流畅的解决本文所涉及的二元二次函数的取值范围问题.

不失一般性,设待求二元二次函数

其中K为待定系数,使(u −AK)x2+(v −BK)xy+(w −CK)y2为一个完全平方式, 进一步由∆= (u −BK)2−4(v −AK)(w −CK) = 0 解的情形(二个解、一个解、无解)探求出s=ux2+vxy+wy2的最值从而得到取值范围.

例1设x,y为实数, 且x2+xy+y2= 3, 求s=x2−xy+y2的取值范围.

解s=x2−xy+y2=k(x2+xy+y2) + (1−k)x2−(1 +k)xy+ (1−k)y2.其中k为待定系数且使(1−k)x2−(1+k)xy+(1−k)y2为一个完全平方式,于是有∆=(1+k)2−4(1−k)2=0,解之得

综上所述,s=x2−xy+y2的取值范围为[1,9].

例2设实数x,y满足x2−2xy+y2= 4, 求:s=x2−2xy −3y2取值范围.

解s=x2−2xy −3y2=k(x2−2xy+y2)+(1−

k)x2+ (2k −2)xy −(k+ 3)y2, 其中k为待定系数使(1−k)x2+ 2(k −1)xy −(k+ 3)y2为一个完全平方式,于是有∆= 4(k −1)2+4(1−k)(k+3) = 0, 进一步得−4k+4=0,k=1.

当k=1 时,由s=x2−2xy+y2−4y2=4−4y2.再由因此s≤4.

例3若实数x,y满足x2+xy −2y2= 1, 求:s=3x2−2xy −y2的取值范围.

解s= 3x2−2xy −y2=k(x2+xy −2y2)+(3−k)x2−(2 +k)xy+ (2k −1)y2, 其中k为待定系数使(3−k)x2−(2+k)xy+(2k −1)y2为一个完全平方式.于是有∆=(2+k)2−4(3−k)(2k −1)=0,解得k1=k2=(x−y)2.

当x=y时,方程组无解,因此故所求s=3x2−2xy −y2的取值范围为

例4若实数x,y满足x2−2xy −3y2= 1,求x2+y2的最小值.

解令s=x2+y2=k(x2−2xy −3y2) + (1−k)x2+ 2kxy+ (1 + 3k)y2, 其中k为待定系数使(1−k)x2+ 2kxy+ (1 + 3k)y2为一个完全平方式, 于是有∆= 4k2−4(1−k)(1+ 3k) = 0, 解之得k1=

当k1=时,

例5已知实数x,y满足4x2+ 6xy+ 9y2= 1, 求4x2−9y2取值范围.

解s= 4x2−9y2=k(4x2+ 6xy+ 9y2) + 4(1−k)x2−6kxy −9(1 +k)y2, 其中k为待定系数使4(1−k)x2−6kxy −9(1 +k)y2为一个完全平方式, 于是有∆= 36k2+ 144(1−k)(1 +k) = 0, 解之得k1=

当k1=时,

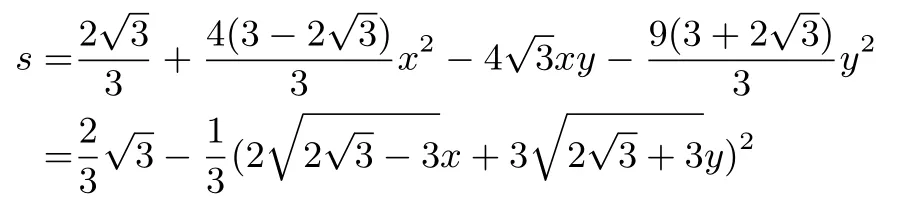
当k2=时,

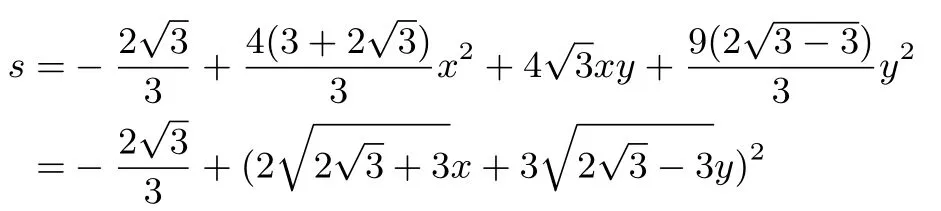
综上所述,4x2−9y2取值范围是