基于梯度搜索法的非线性结构可靠性分析方法

陈鹏霏， 和鹏， 于泰龙， 刘巧伶

(1.长春工业大学 机电工程学院, 吉林 长春 130012; 2.吉林大学 机械与航空航天工程学院, 吉林 长春 130025)

0 引言

工程结构普遍具有非线性特征强和失效概率小的特点。并且，对于复杂的工程结构，其模型通常还具有隐式特征。如何高效、精确地计算隐式非线性结构的可靠度及可靠性灵敏度，一直是结构可靠性分析领域的研究热点之一[1-2]。

目前，常见的结构可靠性分析方法，主要包括解析法、随机模拟法和抽样拟合法等。其中，一次二阶矩法、二次二阶矩法和高次高阶矩法属于传统解析法[3-5]。一般需要根据结构功能函数的Taylor级数展开式，通过保留1阶项，或者高阶项来近似计算功能函数的均值和标准差，进而计算可靠度。因此，采用解析法的前提是需要已知功能函数的显式表达式，故不适用于隐式结构可靠度的求解。随机模拟法主要是以Monte Carlo法为代表，并以此为基础，发展了重要抽样(IS)法和自适应重要抽样法等[6-8]。随机模拟法对于显式或者隐式工程结构的可靠度求解，均具有普遍的适用性，而且在解决强非线性问题时也很有效。然而，随机模拟法的计算精度，是以大量的抽样数据为基础，因此在计算大型复杂结构的可靠度时，其计算效率或成本往往难以接受。针对上述问题，为了高效、精确地计算大型复杂工程结构的可靠度，抽样拟合法[9-13]成为目前可靠性定量分析领域的研究热点。该方法基本思想是，基于响应面法(RSM)、神经网络、Kriging法等，利用有限个样本点建立起输入、响应之间的显式函数关系，来替代原结构的隐式功能函数，再通过传统解析法或随机模拟法计算其可靠度。朱丽莎等[11]将有限元法和人工神经网络技术相结合，研究了随机转子系统中工作参数对转子系统振动可靠性的影响，并进行了排序。佟操等[12]采用Krigring模型提出了一种主动学习的可靠度计算方法，相比同类方法具有所需样本数量少和计算精度高的特点。同时，目前可靠性分析领域采用的抽样拟合法，基于非线性“黑箱”模型(二次多项式、Krigring模型、神经网络模型等)，国内外诸多学者提出了各种选点策略来提高可靠性分析的精度。尤其是近年来，基于主动学习的非线性“黑箱”模型，通过在极限状态方程或极限状态表面附近，选择新训练样本来拟合极限状态方程，而非在整个状态空间内拟合功能函数。因此，其计算精度和计算效率均得到很大的提高[2]。

本文以梯度搜索法为基础，提出一种新的抽样拟合法，来进行结构可靠性灵敏度分析。首先，通过高次梯度搜索法，反复迭代寻找极限状态表面附近的训练样本点；之后，采用多项式函数或响应面函数拟合出结构的极限状态方程，进行可靠度和可靠性灵敏度分析。同时，在数值和工程算例中，将本文所提方法与以往常用方法的分析结果，以及采用Monte Carlo法获得的真值结果进行对比，证明了本文方法具有较高的计算精度和计算效率。

1 一次可靠性分析法

1.1 标准化、正态化状态空间

假设向量x=[x1,x2,…,xn]中包含有n个服从任意分布且相互独立的随机变量，其功能函数为

zX=gx(x1,x2,…,xn)，

(1)

式中：zX表示状态空间X内结构的功能函数；gx(·)为与向量x对应的函数方程。当极限状态zX=0时，则极限状态方程表示以x1,…,xn为坐标轴构成的状态空间X中的一个超曲面。

在工程实际中，对于随机变量xi(i=1,…,n)不服从正态分布的情况，可以采用映射变换的方式来实现随机变量的标准化和正态化[3]。

根据映射变换法作映射变换，则有

Fxi(xi)=Φ(yi)，

(2)

(3)

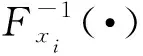
(3)式代入(1)式，可得

(4)

式中：zY表示标准正态空间Y内结构的功能函数；gy(·)为与随机向量y对应的函数方程。

所以，任意非正态分布随机变量均可转化为标准正态分布随机变量。故此，本文仅讨论相互独立的正态分布随机变量情形。

1.2 基于经典验算点法的可靠性分析

图1 极限状态方程和验算点示意图Fig.1 Sketch map of limit state equation and checking point

若已知结构的功能函数，则失效概率[15]为

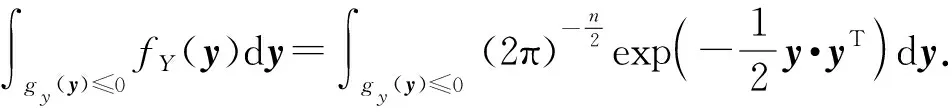
(5)

根据可靠度指标β的定义，可知验算点对应的β*为

(6)

依据Taylor展开法，将(4)式所示的功能函数在验算点y*处展开为线性化方程：

(7)

式中：∂gy/∂yi=∂gx/∂xi·∂xi/∂yi，∂gx/∂xi在随机向量x的验算点x*处计算，∂xi/∂yi在随机向量y的验算点y*处计算，根据(3)式可知：

(8)

φ(·)为标准正态概率密度函数，fxi(·)为变量xi的概率密度函数。

(7)式中右边各项均为随机向量y的线性组合，因此zYL也应服从正态分布，其均值μzYL和标准差σzYL分别为

(9)

式中：σyi为变量yi的标准差。

故结构的失效概率可近似表示为

Pf≈P{zYL≤0}=Φ(-βzYL)，

(10)

式中：βzYL为线性化极限状态函数zYL的可靠度指标[16]，且

βzYL=μzYL/σzYL.

(11)

根据(7)式、(9)式和(11)式，可推导出标准正态空间Y内验算点y*的坐标值：

(12)

式中：cosθyi称为验算点重要度系数，

(13)

最后，根据(3)式，可得基本随机向量x的验算点x*. 由推导过程可知，当采用一次可靠性分析方法计算失效概率Pf时，将极限状态方程线性化是造成误差的主要原因。

2 梯度搜索法计算样本点

2.1 一次梯度搜索

由(12)式可知，一次可靠性分析中的验算点可通过重要度系数逐步迭代获得。因此，根据经典验算点法(FORM)，关于非线性结构的一次梯度搜索过程如下：

1) 依据工程经验找到失效域中一点，或直接将均值点x(1,0)确定为初始点，并将其转换为标准正态空间内点y(1,0)；

3) 通过以上过程反复迭代nS1次，最终确定出贴近极限状态曲面，且满足精度要求的抽样点y(1,nS1)作为一次梯度搜索的输出响应点y*(1)，且可由(3)式将其转化为状态空间X中的点x*(1).

2.2 高次梯度搜索

通过一次梯度搜索获得的响应点x*(1)，就是FORM中所说的验算点[14]。根据点x*(1)建立的近似极限状态方程属于线性化方程，这是一次可靠性分析方法得到的失效概率Pf存在计算误差的根本原因。因此，还需要在此基础上获得贴近极限状态曲面的其他样本点。具体过程如下：

1) 根据(7)式过响应点y*(1)建立结构极限状态曲面的1阶线性平面方程：

(14)

(14)式为标准正态空间Y中的一个超平面。

2) 以点y*(1)为中心，选取合适的r作为半径，构建标准正态空间Y中的超球面方程：

(15)

(16)

式中：j=1,…,k-1,k+1,…,s-1,s+1,…,n.

图2 基于梯度搜索法获取极限状态曲面附近样本点流程框图Fig.2 Flow chart of obtaining the sampling points near limit state surface by gradient search method

图3 基于梯度搜索法的抽样点分布与拟合函数示意图Fig.3 Sketch map of sampling point distribution and fitting function based on gradient search method

超球面半径r的选取，与参数空间内随机变量的标准差有关，且影响结构失效概率计算过程中的效率和收敛性。当初次搜索时，可取步长系数α=1.0，之后逐次翻倍。经过若干次迭代搜索之后，若半径r≥3rR时仍不能获得令人满意的结构失效概率，可将α值减半，即令α=0.5，重新进行取点搜索，并令α每次增长奇数倍；当半径r再次超过3rR时，令α继续减半，且每次增长奇数倍，直到获得满意的结构失效概率值为止。

2.3 隐式功能函数偏导数的计算

在获取梯度信息和可靠性灵敏度分析过程中，偏导数的计算都至关重要。对于显式功能函数，可直接通过求导来计算偏导数。而对于隐式功能函数，则一般通过差分法来计算函数gx(x)的偏导数[17]。这里，常用的差分法包括中心差分法和向前差分法两种。中心差分法：

(17)

式中：Δxi表示向量x中变量xi的微小变化量；功能函数gxi+Δxi=g(x1,…,xi+Δxi,…,xn)；功能函数gxi-Δxi=g(x1,…,xi-Δxi,…,xn)。

向前差分法：

(18)

式中：功能函数gxi=g(x1,…,xn)。

因此，在计算隐式功能函数的偏导数时，两种差分法所需的抽样点数N*略有不同。采用中心差分法，N*=n0(2n+1)+1，n0为迭代次数；采用向前差分法，N*=n0(n+1)+1. 显然，中心差分法所需抽样点数较多，但其计算精度要优于向前差分法。

同时，在采用差分法计算偏导数时，差分步长的选取对于计算精度起到重要作用。步长选取过大，则误差变大。但是，若步长选取过小，在实际工程中又会受到测试仪器精度等级的限制，影响输出值的读取精度，同样会造成误差。因此，在实际工程中，步长的选取需要参照测试仪器的最高测试精度等级，即在保证测量精度的前提下，步长应越小越好。本文在采用差分法计算偏导数时，考虑到各随机参数的分布变化特征，以参数标准差的1/15作为求取偏导数的差分步长，来进行计算的。

3 可靠度及可靠性灵敏度计算

3.1 非线性极限状态方程的拟合

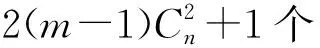
(19)

(20)

因此，当抽样的阶次m无限大时，拟合函数方程所表达的超曲面，与结构真实的极限状态方程之间，误差将趋于0，即

(21)

3.2 计算可靠度及可靠性灵敏度

根据结构可靠性分析理论，失效概率Pf为基本随机变量y=[y1,y2,…,yn]的联合概率密度函数在失效域F内的积分[8]，即

(22)

式中：失效域F={y:y∈gy(y)≤0}。

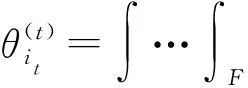
(23)

(24)

式中：σt为第t个随机变量的标准差。

对于复杂隐式极限状态函数zY=gy(y)，失效域边界gy(y)=0无法解析表达。此时，(22)式和(23)式的积分只能采用数字模拟的方法来进行计算，计算量非常大。但是，依据(19)式，可获得结构失效域边界函数的近似解析表达式，即y(y)=0. 因此，可直接采用数值积分的方法来进行求解，将大大减小计算量，提高计算效率。

4 算例

本节将通过数值和工程算例，来验证所提方法的计算精度和成本效率。

由图3可知，将均值点作为一次梯度搜索的初始点，可获得对应的验算点。根据该验算点，即可获得1阶线性方程。选取适当步长，在1阶线性方程上可继续取2个2次抽样初始点，继续利用梯度搜索法可获得另外2个对应的2次验算点。根据这2个2次验算点和上述验算点(此时，共3个点)，可获得抛物线方程，即2阶曲线方程。将步长加倍后，在1阶线性方程上继续取2个3次抽样初始点，于是又可获得2个3次验算点。根据3次验算点、2次验算点和验算点(共5个点)，可拟合得4阶曲线方程。至此，该4阶曲线方程已与极限状态方程非常近似。若满足精度要求，即可跳出程序循环，结束计算。否则，还可以继续搜索获得更高阶的拟合曲线方程。

采用本文所提方法算得的失效概率结果Pf、随机变量灵敏度结果，以及所需要的抽样次数N*如表1所示。为便于比较，表1中同时列出了采用Monte Carlo可靠性抽样(MC_RS)法、IS法、RSM，以及FORM的计算结果。并且，将MC_RS大样本模拟法获得的计算结果作为精确解(即真值)，与其他方法相比较，可得到各种分析方法的绝对误差和相对误差(相对误差=绝对误差/真值)。

表1 算例1可靠性灵敏度分析结果和抽样点数一览表

由表1数据可知，在各种可靠性灵敏度计算方法中，与MC_RS法算得的真值比较，IS法计算结果的误差较小，因此精度较高。但是，需要的抽样次数也较大，因此并不适用于计算量较大的大型复杂结构可靠性灵敏度分析。而RSM采用含有交叉项的多项式函数来拟合出响应函数，尽管计算效率很高(对于算例1，根据中心复合法抽样，在两个变量情况下仅需5个样本点)，但是RSM抽取样本点的目的是为了构建结构的状态方程，而非极限状态方程，因此计算精度较差。由表1可知，对于强非线性结构，RSM的计算结果几乎失真。FORM通过迭代计算，获得极限状态曲面上联合概率密度值最大的点，并将其作为验算点，把通过验算点的1阶线性平面近似看做结构的极限状态曲面。对于弱非线性结构可靠度计算而言，FORM的计算精度和效率均尚可。但是，对于如算例1所示的强非线性结构，FORM的计算精度并不令人满意。

为了更加清晰地比较RSM、FORM与本文所提方法在计算精度和效率(即抽样点数)方面的差别，在采用本文方法分析算例1时将其所经历的抽样点数和对应结果列于表2中。

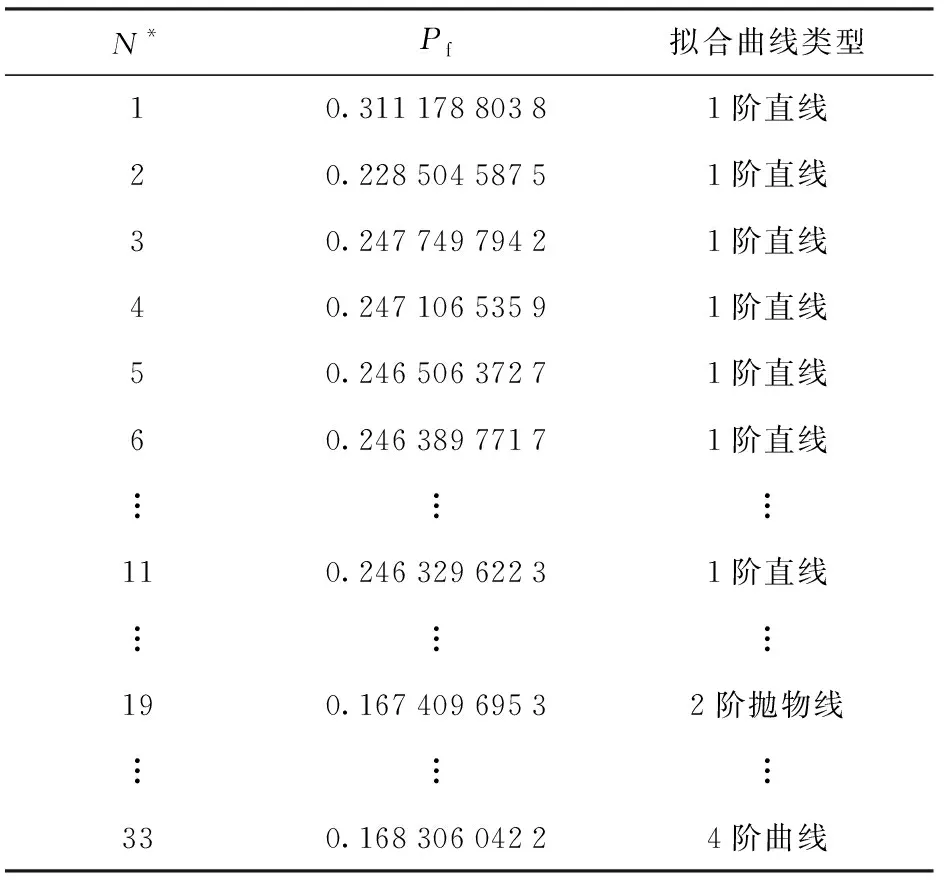
表2 算例1抽样点数和对应结果一览表

综上所述，本文所提方法是在FORM的基础上，通过梯度搜索不断获得强非线性结构极限状态曲面上的样本点，最后采用合适的拟合函数拟合极限状态方程，计算可靠性灵敏度。表1中数据显示，无论是失效概率，还是各参数的可靠性灵敏度，本文所提方法的计算精度，均与MC_RS法计算的真值非常贴近，因此能够对工程实际产生有效的指导作用；同时与解决强非线性结构可靠性灵敏度分析的其他方法(如IS法)比较，本文所提方法的抽样点数很少。所以，更加适用于计算工作量较大的大型复杂结构的可靠性灵敏度分析。

(25)

图4 液压缸运动的力学模型Fig.4 Mechanics model of hydraulic cylinder

当液压缸低速运动，即油液的平均流速v较小时，由(25)式可知，其运动呈现出显著的非线性特征。随着v的变化，其运动状态一般可分为边界润滑、混合润滑和动压润滑3种情况[19]，对应的速度时域图像，分别如图5(a)、图5(b)、图5(c)所示。

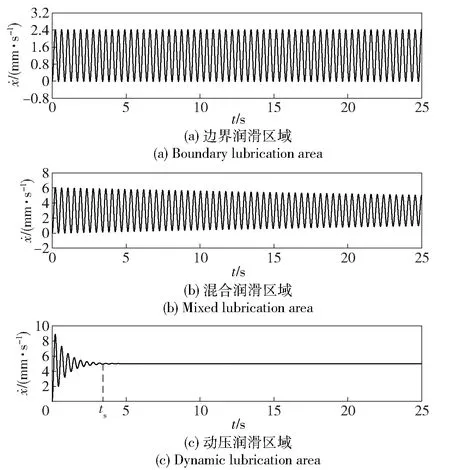
图5 不同润滑区域的活塞瞬时速度时域图像Fig.5 Time-domain images of piston instantaneous speed in different lubrication areas

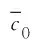
g(XH)=tslim-ts，

(26)

采用本文所提方法，对(26)式进行可靠性灵敏度分析，计算结果如表3所示。同时，将MC_RS大样本模拟法、IS法、RSM和FORM计算出的可靠性灵敏度结果值，一同列入表3中。在本算例的数值计算过程中，涉及偏导数的计算，采用的是中心差分法。虽然中心差分法的抽样次数较向前差分法多(本例若采用向前差分法，则抽样点数为27)，但计算精度较高。

表3 液压缸活塞运动可靠性灵敏度计算结果及抽样次数一览表

通过对比表3中数据可知，采用本文所提方法计算的失效概率和可靠性灵敏度，与MC_RS大样本模拟法获得的真值相比，均比较接近，能够正确反映液压缸的运动可靠性，及各参数对可靠性的影响情况。同时，从抽样次数来看，本文所提方法无疑具有更高的计算效率，尤其适用于计算工作量较大的大型非线性结构可靠性灵敏度分析。

此外，如表3所示，通过对比其他结构可靠性分析方法可知，由于IS法的计算精度和效率严重依赖于重要抽样密度函数的选取，而重要抽样密度函数一般需凭经验选取。所以，在不明确失效域的情况下，重要抽样法的计算精度和效率会大打折扣。因此，在本算例中IS法的计算精度和效率均不如本文方法。RSM虽然在计算成本(或抽样点数)上少于本文方法，但是RSM法采用有限个样本点拟合出的响应面函数，来对结构整个状态空间内的功能函数进行替代，很多情况下其计算精度，尤其是各随机参数灵敏度的计算精度难以满足工程需要。在本算例中，RSM的失效概率计算精度最低；而其随机参数灵敏度的计算结果，与真值结果(采用MC_RS法的计算结果)相比，由于数量级相差过大，故已失真。这里，FORM的抽样点数少于本文方法。但是，如前所述，FORM属于一次可靠性分析方法，由于其在计算过程中采用线性平面直接替代结构真实的极限状态表面。因此，当结构的非线性特征越强时，其计算精度会越差。由于本算例属于非线性工程结构算例，故FORM在计算精度上不如本文方法。

5 结论

本文针对强非线性结构，提出一种基于梯度搜索法的可靠性灵敏度分析方法。通过逐次迭代搜索极限状态表面上的样本点，拟合结构极限状态方程计算可靠度及可靠性灵敏度。通过算例分析，得出主要结论如下：

1)与MC_RS和IS等随机模拟法相比，本文所提方法具有计算成本小、效率高的特点，尤其适用于大型复杂工程结构的可靠性灵敏度分析。

2)与通过状态空间中样本点拟合结构功能函数或极限状态方程的抽样拟合法相比，本文所提方法具有更高的计算精度。