基于局部时均Navier-Stokes模型的分域计算方法

罗倩， 胡常莉

(南京理工大学 能源与动力工程学院, 江苏 南京 210094)

0 引言

随着计算机技术日新月异的发展，借助数值计算方法研究流体力学相关问题，越来越受到人们的青睐。尤其是工程实际中的复杂流动问题，比如各类流体机械、船舶、水中兵器等工程领域，往往涉及湍流、相变、可压缩等多个物理过程，这对数值模型的发展提出了很大的挑战。其中，湍流模型直接关乎复杂流动数值方法的预测精度。

一直以来，方柱绕流与空化流动是流体力学研究中的经典与热点问题，备受研究者的关注，建立合适的湍流模拟方法也是其数值研究的重点[1-2]。张显雄等[3]对比了5种湍流涡黏模型在方柱绕流的数值模拟中的求解差异，结果表明：标准k-ε(k为湍动能，ε为湍流耗散率)湍流模型的计算结果程度整体弱于其余湍流模型；剪切应力输运(SST)k-ω(ω为湍流频率)模型的计算结果优于其余湍流模型。Long等[4]、Ji等[5]、杨龙等[6]应用大涡模拟(LES)方法进行了空化流动的数值计算，发现LES方法可以准确模拟出非定常空化流动的流动特性。但LES方法计算资源消耗大。随着数值研究的深入以及对湍流计算要求的提高，许多混合湍流模型被提出和应用[7-8]。局部时均Navier-Stokes(PANS)模型是由Girimaji[9]提出的，一种可从雷诺时均Navier-Stokes(RANS)平滑过渡到直接数值模拟(DNS)的混合湍流模型，被广泛应用于流动研究中。Razi等[10]应用PANS模型研究了周期性山型流道内的流动分离问题。王亦晓等[11]采用PANS模型研究了簸箕形进水流道的水力特性。Busco等[12]采用PANS模型研究了压水堆燃料束间隔格栅间的复杂湍流结构。刘跃等[13]应用该模型研究了绕圆柱流动过程，结果表明PANS模型可以捕捉到丰富的湍流结构。该模型在空化流动特性的研究中，也有较好的模拟效果[14-15]。但标准PANS模型对整个流场是一致性求解，未能体现桥接模型的优势。因此，众多学者对标准PANS模型作了进一步的发展与修正。Luo等[16]提出一种基于k-ω修正的PANS模型，开展了绕NACA66水翼的空化流动，讨论了滤波器参数fk不同取值对瞬态空化涡流动预测的准确性。Zhang等[17]采用PANS模型研究了最大密度比和控制参数fk对预测水翼空化流动的影响，发现提高最大密度比和降低fk值可以获得更好的结果。Huang等[18]根据局部网格大小和湍流长度对fk进行调整，实现在空间和时间上改变fk分布，使得PANS模型对空化湍流流动的预测能力获得了明显的提高。Hu等[19]考虑密度变化特点发展了一种修正PANS模型，依据当地云状空化状态对控制参数进行动态调节，获得精确结果的同时提升了计算效率。

本研究基于标准PANS模型中控制参数fk的取值特点，提出一种分域计算方法，实现了同一流场采用不同湍流模型求解的效果，即可对关注区域进行精细求解，其他区域降低求解要求，减少计算消耗。通过对商业软件CFX的二次开发实现所提方法，并应用其分别进行了柱体绕流和绕水翼空化流动的数值研究，分析了方柱绕流的流场特性和水翼云状空化流动的空泡形态和动力特性，并与实验结果对比，验证了该方法在单相湍流流动和两相湍流流动应用中的可行性。

1 数值计算方法的控制方程

1.1 控制方程

本研究的基本控制方程为连续性方程和Navier-Stokes方程：

(1)

(2)

1.2 标准PANS模型及其分域思想

PANS模型的湍动能ku和耗散率εu的输运方程分别为

(3)

(4)

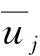
(5)

Cμ为黏度相关系数，Cμ=0.09；σku、σεu为Prantdl数，

(6)

σk=1.0,σε=1.3；Pu为湍动能生成项；

(7)

Cε1=1.44，Cε2=1.92.

(8)

PANS模型的两个控制参数[20]分别定义为

(9)

在高雷诺数的流动中fε值通常取1：当fk=1时，说明湍流控制方程复原到RANS模型；当fk=0时，表示数值计算过程没有湍流模型的引入，为直接求解的方式。PANS模型可以实现任何滤波器尺度对湍流流动的求解[9]，fk的取值控制滤波尺度大小，随着fk的减小，PANS模型可释放更多的湍流运动尺度。根据这一特点，本研究将整个计算域化分为多个区域来计算，以实现关注流域fk取小值进行计算，其他区域fk取较大值进行计算。

1.3 无量纲参数

本研究涉及的无量纲数主要有雷诺数Re、升力系数CL、阻力系数CD、压力系数Cp和空化数σ，以及对升力系数随时间变化曲线进行快速傅里叶变换(FFT)所得对应的斯特劳哈数St，定义分别为

(10)

(11)

(12)

(13)

(14)

(15)

式中：u∞、p分别为来流流速和当地静压强；L、A对应的是本文研究对象的特征长度和有效面积；υ为运动黏度；ρ为流体密度；FL、FD为研究对象所受的升力和阻力；p∞、pv分别为环境压强和饱和蒸气压；f为空穴周期变化的频率。

2 绕二维方柱流动的数值计算

2.1 计算域设置和网格无关性验证

图1(a)为绕方柱流场计算域示意图。方柱边长D为0.05 m，计算域长为50D，下边界与方柱距离为12D. 计算流体为25 ℃的水，采用速度入口、压力出口，对应雷诺数Re=22 000，流域上下边界和方柱壁面为无滑移壁面。图1(a)中的红色虚线将整个计算域划分为方柱近流区和远流区两部分进行计算，即近流区fk取值为0，远流区fk取值为1.

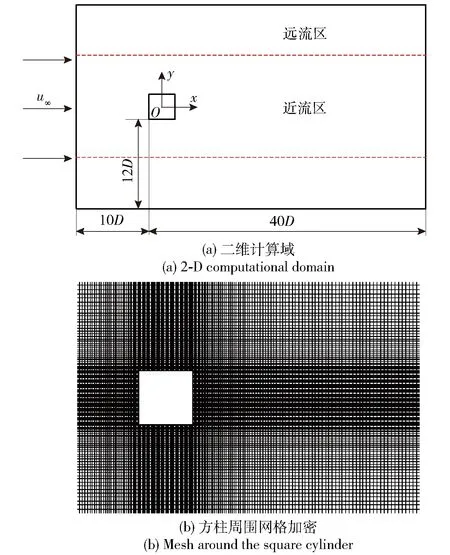
图1 方柱绕流计算域及网格示意图Fig.1 Computational domain and mesh around the square cylinder

图1(b)为方柱周围的网格分布情况，计算域采用结构化网格，并对方柱近壁面区域进行网格加密处理。图2给出了网格1(节点数240 160)、网格2(节点数304 974)、网格3(节点数525 352)和网格4(节点数973 824)4套网格下的数值计算结果。由图2可以看出，随着网格数目的增加，不同网格之间对应的方柱升力系数变化幅度减小，而网格数量的增加必然会加大计算消耗。因此，综合考虑计算的适用性和经济性，本文选用网格2进行绕方柱流动的数值研究。

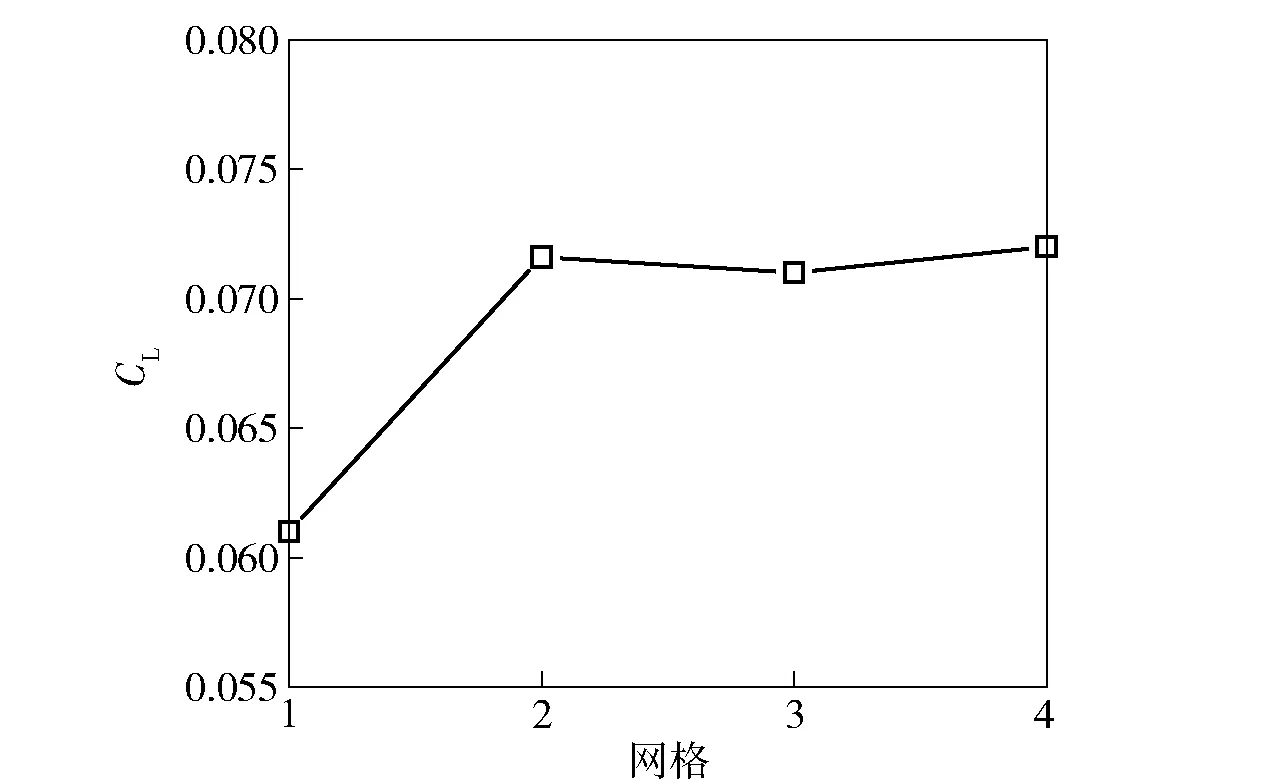
图2 不同网格计算所得升力系数Fig.2 Lift coefficients of different meshes

2.2 方柱绕流的结果讨论

图3(a)为绕方柱流动过程中的瞬时涡量图，流体流经方柱时，方柱上下表面交替产生旋涡，旋涡随流动发展脱落，小涡变大涡向下游运动形成卡门涡街。图3(b)为时均流向速度u云图，从图中可以看出，由于方柱边角发生流动分离，产生分离涡，方柱近壁面区域存在较大的速度梯度，且受卡门涡街的影响，方柱正后方流场区为低速区，其速度明显小于两侧流场的速度。

图3 涡量和速度云图Fig.3 Contours of vorticity and velocity-u

至今为止，已有诸多学者对较大雷诺数下的方柱绕流进行了实验和数值研究，表1列出了实验研究和DNS方法以及本文计算方法所得的时均阻力系数和斯特劳哈数。通过对比可以看出，本文方法得到的时均阻力系数与文献[21-22]中的实验值和DNS方法结果相差较小，基本一致，而斯特劳哈数比实验值和DNS方法结果值略大些，误差在7%～16.4%左右。这是因为湍流本身具有三维性，而二维数值计算会造成流动特征频率的过预测。

图4(a)和图4(b)分别为方柱表面时均压力系数分布和中心线上时均流向速度沿x轴方向的分布。其中图4(a)中横坐标表示位置，与图中方柱各边对应，为了便于展示，时均流向速度均以初始的流体速度u0作无量纲处理。可以看出，本研究计算所得的方柱表面压力系数的变化规律与实验和DNS方法结果基本一致，即方柱来流方向中心点处所受压力最大，方柱边角产生流动分离导致压力显著降低。从图4(b)中可看出，本文方法和DNS方法中心线上的时均流向速度均为由0 m/s减小至最小值，随后渐进增加的变化趋势，与实验结果较为一致。然而对比发现，本文方法获得的中心线上时均流向速度最小值与实验值更为接近，且在x/D<3范围，即流动较为强烈的区域，本文方法时均流向速度的变化相比DNS方法结果与实验结果更吻合。

表1 本文方法与前人实验和数值结果的比较

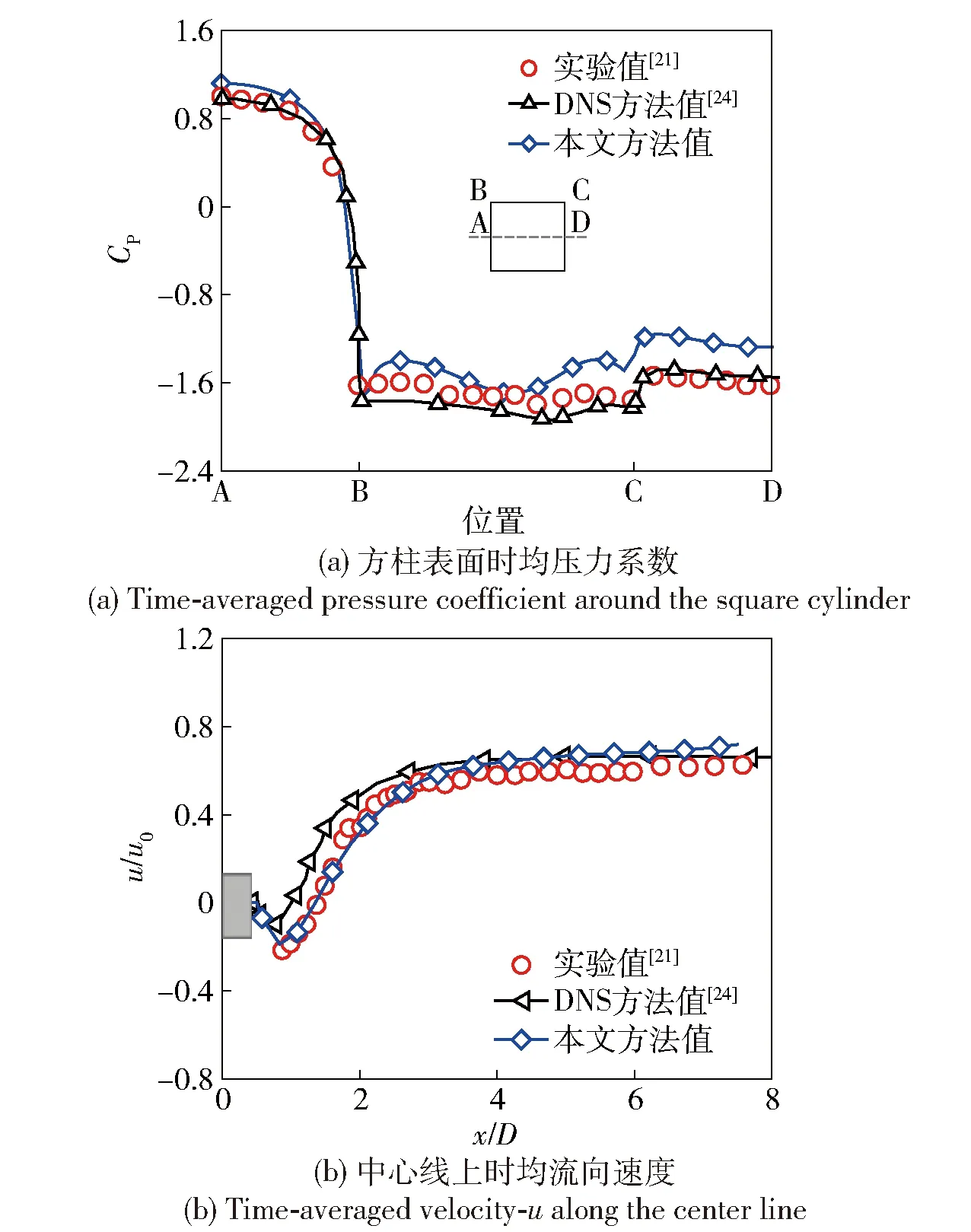
图4 时均压力系数和流向速度分布情况Fig.4 Distribution of time-averaged pressure coefficient and velocity-u

图5为不同截面处时均流向速度沿y轴方向的分布，对应的截面位置如图3(b)中黑色虚线所示。与实验结果对比可看出，数值结果与实验结果较为吻合。不同截面位置的时均流向速度分布特点均是由中心位置沿y轴方向渐进增大。x/D=0处，即方柱中心位置，由于流体流过方柱边角位置发生流动分离，产生分离涡，导致方柱近壁面速度最小且为负值，在剪切层处速度为最大值。而x/D=1，如图3(b)中黑色虚线所示，该处对应的是方柱绕流尾流的回流区域，此处的时均流向速度从负值开始渐进增大。随着向下游流动，逐渐远离回流区的尾流位置，如图3(b)中x/D=3、x/D=8位置处，其剖面处中心位置的最小流向速度均已由负值增大到正值，流向速度沿y轴方向渐进增加至远流场基本保持平缓。

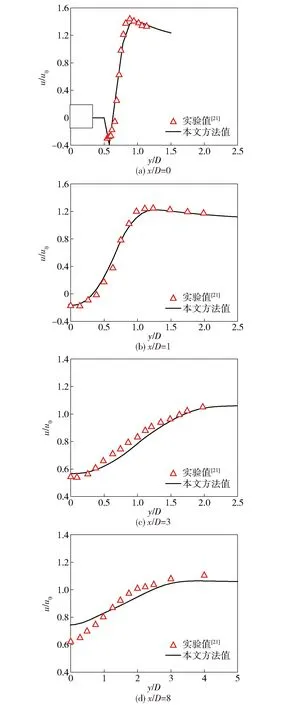
图5 不同剖面时均流向速度u的对比Fig.5 Comparison of time-averaged velocity-u at different sections

3 绕二维水翼非定常空化流动数值计算

目前，对于非定常空化流动的数值计算方法，基于均质流框架并耦合Zwart等[25]空化模型和湍流模型的方法被广泛应用，可详见文献[7,18,26-28]。本文也采用上述方法耦合分域计算的PANS模型对绕Clark-y水翼的非定常空化流动进行了数值计算。

3.1 计算域设置与方法说明

图6(a)和图6(b)分别给出了计算域设置和局部网格示意图，计算域的选择与实验段[29]相同。Clark-y翼型的弦长C为0.07 m，计算域长为10C，边界条件采用速度入口，压力出口，流速为u∞=10 m/s，对应的雷诺数Re=7×105，调节出口压力设定空化数σ=0.8，流动区域上下边界为自由滑移壁面，翼型表面采用绝热、无滑移壁面边界。计算域网格采用结构网格划分，对翼型近壁面采取了网格加密处理，近壁面y+值在5左右，满足壁面函数要求。

PANS模型在绕水翼云状空化流动模拟中控制参数fk的分域，如图6(a)所示。将计算域分为3个区域：红色虚线标注的近壁面区域E1，其控制参数取fk=0；远流场区域E3，其控制参数取fk=1；E2为过渡区域，采用前人研究使用较多的fk=0.2模型进行计算。

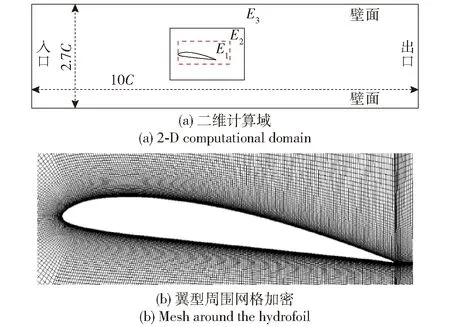
图6 计算域设置及网格示意图Fig.6 2-D computational domain and mesh around the hydrofoil

3.2 绕水翼非定常空化流动的结果讨论

表2给出了绕Clark-y水翼云状空化流动一个周期T内空泡形态的演变过程，其中水翼前端附着空泡刚开始产生时为t0时刻。对比发现，数值计算与实验结果较一致地捕捉到附着空泡从产生到脱落的准周期变化过程，即水翼前端开始产生附着空泡。附着空泡随时间沿流动方向发展至最大，在回射流作用下，附着空泡逐渐出现断裂脱落，在t0+0.7T时刻，水翼附着空泡呈现出一种藕断丝连的状态，断裂后空泡随流动向下游运动，脱落空泡形态也由沿展向方向的扁长型发展成厚度较大的团状型。

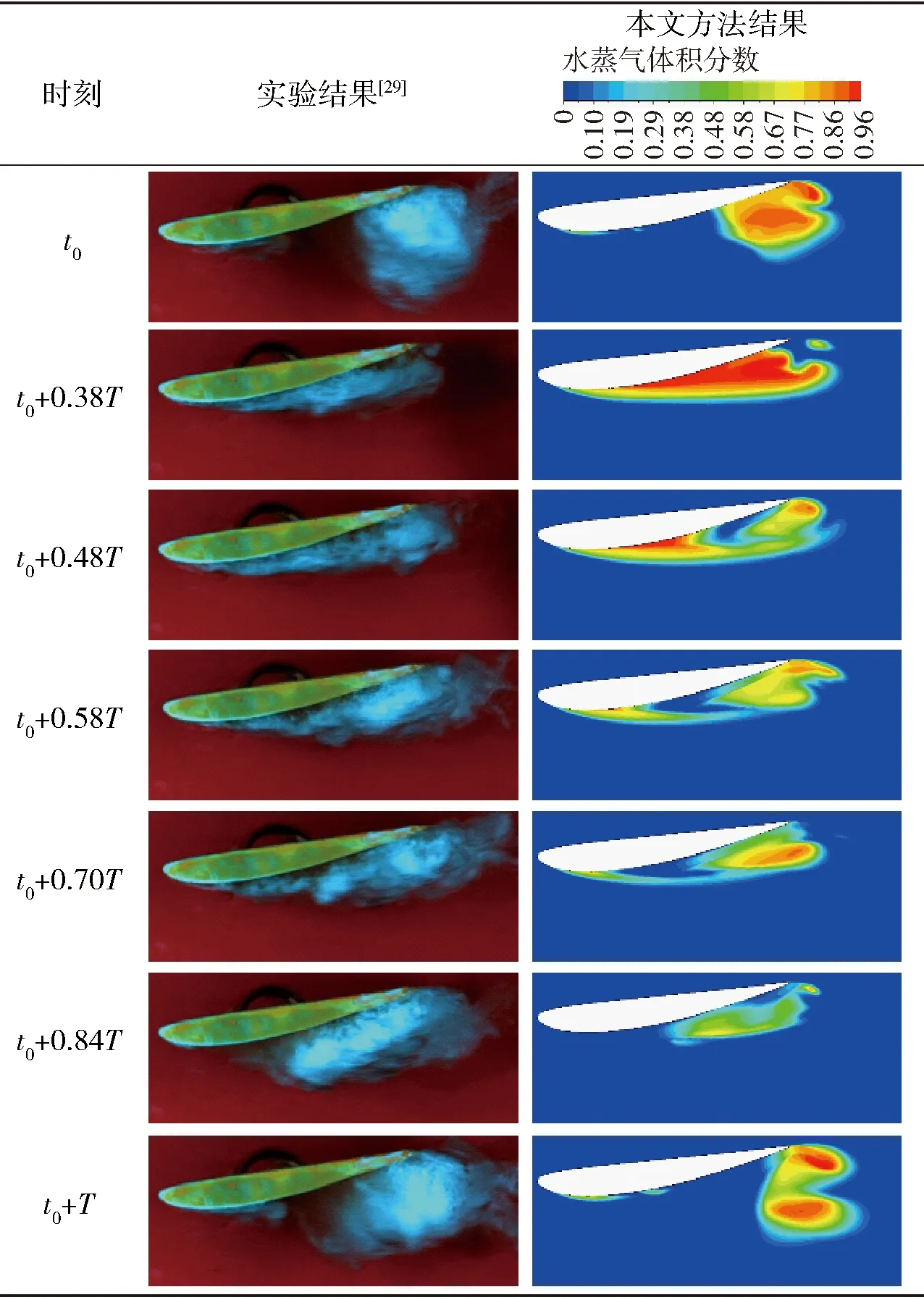
表2 二维水翼空泡形态随时间变化

图7(a)和图7(b)分别为Clark-y水翼升力系数曲线及其功率密度谱分析。与实验结果对比发现，数值计算可以很好地模拟出水翼升力系数曲线随时间的波动规律，与空泡形态发展过程相对应而呈周期性变化，另外，二者的时均升力系数也基本一致。将水翼升力系数通过FFT获得功率谱密度图，图7中功率密度最大值反映了特征频率，对比发现，数值计算所得斯特劳哈数(St=0.25)是略大于实验值(St=0.22)的，这是由于实验中存在一定的壁面效应会导致空化在非定常演变过程中产生三维U形空泡团的断裂脱落，从而采用二维模型的数值计算易过预测其特征频率。

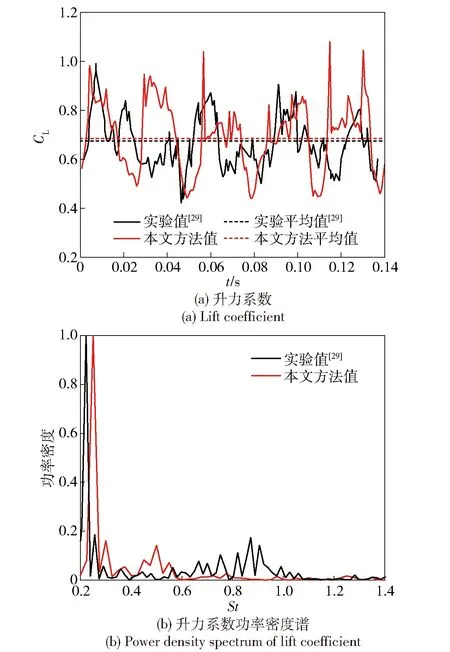
图7 翼型升力系数曲线及功率密度谱分析Fig.7 Lift coefficient and power density spectrum analysis of hydrofoil

4 结论

本文基于标准PANS模型中控制参数fk的取值特点，发展了一种对流动区域进行分域计算的方法，应用该方法分别计算了湍流流动中较为经典的方柱绕流和绕水翼非定常空化流动，并基于实验结果对比分析了该方法的可行性。得出主要结论如下：

1)基于PANS的分域计算方法可针对流场不同区域，通过设置控制参数fk的不同取值，实现对所关注流动区域的精细模拟。

2)对于较大雷诺数下的绕方柱单相流动，基于PANS的分域计算方法所得的时均阻力系数、方柱表面压力系数和流向速度等，与DNS和实验结果均基本吻合；对于绕Clark-y水翼的非定常空化流动，该方法可获得与实验较一致的空穴形态演变过程和水翼升力系数的变化规律。