装备伴随抢修任务分配决策方法

王少华， 吕会强， 董原生， 张远

(1.陆军装甲兵学院 装备保障与再制造系， 北京 100072； 2.陆军装备部 信息保障室， 北京 100072)

0 引言

在信息化战争中，武器装备的威力和命中精度将大大提高，装甲装备的损伤机率将随之提高。作为部队补充和恢复战斗力的主要手段，战场伴随抢修能能够及时有效地恢复部队战斗力，通过科学决策提高伴随抢修的实施效率，是装备保障决策者关注的重点。

伴随抢修主要根据作战力量部署，在战场前沿编设多个小规模的伴随抢修组，利用战斗间隙，前出至现地的多个抢修作业点遂行抢修任务，抢修具有力量规模小、风险高、任务强度大、时间短的特点。在有限时间内，伴随抢修力量往往无法完成全部的抢修任务，在此背景下，如何通过科学决策分配伴随抢修任务，对伴随抢修任务的成败起着决定性的作用。对于多抢修组，决策者面临的决策问题主要有两个内容，一是如何在抢修任务集合中选择任务并将其分配给各抢修组，二是为每个抢修组确定最佳的抢修任务实施顺序，确保抢修任务又多又快地完成。伴随抢修决策受到决策目标、抢修任务量、抢修时间、战场环境等诸多因素的影响，必须采用客观的决策方法进行决策，以尽量降低主观决策容易带来的潜在风险[1-3]。

目前，很多学者已经针对不同类型的决策问题提出了相关的战场抢修决策优化方法。在未考虑抢修时间限制的情况下，田冕等[4]采用层次分析法、刘利等[5]采用贝叶斯网络理论、何晓晖等[6]采用模糊理论提出了多装备抢修顺序决策方法。王雷[7]在考虑抢修时限的条件下提出了抢修顺序决策方法，但模型未从指挥角度考虑任务匹配问题，而且抢修时限设定为唯一值，与战场抢修决策者面临的现实问题还有一定的差距。针对这一不足，本文考虑多抢修组完成多个抢修任务，且考虑单装抢修时限的独特性，对典型伴随抢修任务分配决策方法进行研究。

1 装备伴随抢修决策问题分析

装备伴随抢修具有时效性强、随机性和不确定性高的特点[8]。装备战场伴随抢修的基本特点[9]是：

1)一个抢修队通常包含若干抢修组，保障一个作战方向或一个作战地域的装备抢修任务。每个伴随抢修通常依车编组，携带必要的器材备件和机工具等实施抢修。

2)装备伴随抢修任务强度通常较高，即在给定的时间窗口内，抢修组通常无法完成所有的抢修任务。

3)伴随抢修时机通常是战斗间隙或战斗转换时，抢修作业点通常分散在多个地点，每个作业点通常须在规定的时限内完成抢修，否则需要转运后送。

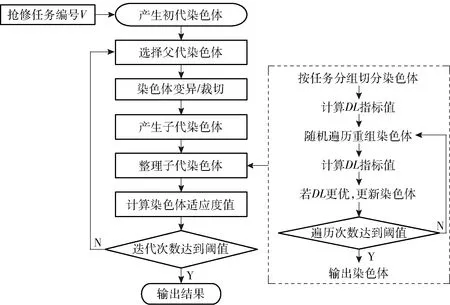
根据上述特点，假定当前所有损伤装备及其位置已经明确，每个损伤装备的抢修耗时以及修竣时限同时给定，抢修决策者需要在所有的待修装备中选择适量的任务，并为每个抢修组分配抢修任务；而后为每个抢修组确定抢修任务的实施顺序，以最大限度地修竣损伤装备。图1所示为伴随抢修行动流程。

如图1所示，从实施过程看，伴随抢修主要按照技术准备并前出、按既定顺序实施抢修作业和撤收的步骤实施。对于一个抢修组，给定抢修任务的情况下，抢修决策的内容主要是各任务的抢修顺序。

当面对多个抢修组以及抢修任务时，决策者需要根据各作业点的抢修耗时、修竣时限、所处位置做出决策，其决策目标是最大限度地发挥各抢修组的能力，在修竣时限范围内完成尽量多的抢修任务[10]。

由上述分析可知，装备伴随抢修决策主要是根据抢修组数量，在待修任务集合中选择任务并确定抢修顺序，使修竣装备数量最大化。

2 装备伴随抢修决策建模

如第1节所示，多任务—多抢修组条件下，装备抢修任务分配决策实际上是抢修任务分组和抢修顺序的联合决策。

2.1 伴随抢修时序过程模型

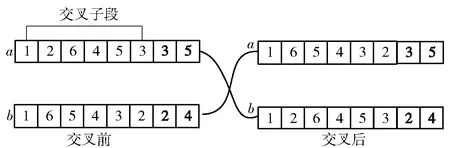
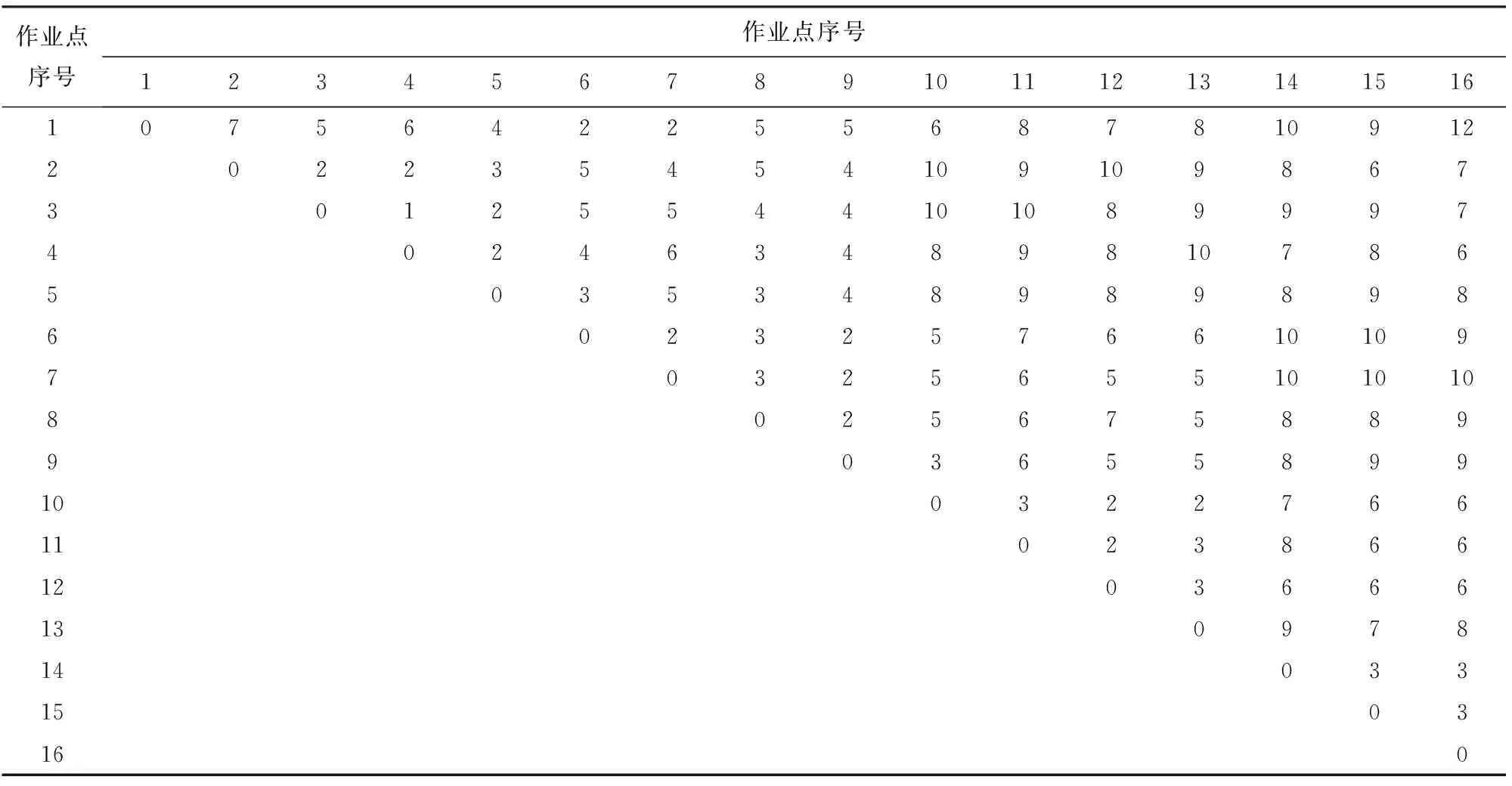
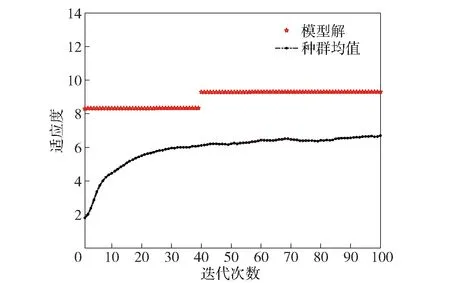
问题描述：假设当前待修装备的总数量为Ntot，抢修组数量为M(M

将抢修组的出发点编号为1，其他抢修作业点按照从2至Ntot+1的顺序赋予唯一的初始任务编号，即抢修作业点初始任务编号为1，2，…，Ntot+1.

定义抢修时间向量P=(p1,p2,…,pi,…,pNtot+1)，其中pi是作业点i的抢修耗时，假设每个抢修作业点所需的抢修时间是确定的，即P为常值向量。

定义修竣时限向量D=(d1,d2,…,di,…,dNtot+1)，其中di是作业点i的抢修任务完成时限，即该作业点允许的最晚修竣时间，这里将修竣时限设为硬约束，即若无法在修竣时限内修复损伤装备，则不抢修该装备。

定义机动时间矩阵E={ei,j|1≤i,j≤Ntot+1}，ei,j表示由作业点i向j机动所消耗的时间(min)，有ei,j=ej,i(2≤i,j≤Ntot+1)，ei,i=0.

对于这个给定的任务集合，可以选择不同的抢修顺序，抢修组的机动路线将对应变化，抢修任务的完成状态和数量也将随之变化。假定按照作业顺序对抢修组1分配到的任务进行排序，排序后的任务为{vl,1，…，vl,k，…，vl,NAi+1|1≤vl,k≤Ntot+1},其中vl,k为抢修组l所分配任务中排序优先度为k的作业点初始任务编号，由于各抢修组必须从配置点出发，因此对于任何抢修组有vl,1=1，其他任务的顺序为随机变量，且1个抢修组内各任务编号不重复，即保证一个任务只能被执行一次。

定义修复时间向量Sl，与给定的任务分配方案相对应，Sl={sl,k|k∈1,2,…,NAl+1}，sl,k表示作业点vl,k的任务完成时刻，随抢修顺序逐步累加。由于抢修时出发点都相同，因此有

(1)

不同的抢修任务排序方案决定着每个任务的完成时间，当任务完成时间早于预设的修竣时限时，表示该任务可如期完成，否则表示该任务将延迟完成。

根据作业点编号可得到抢修组l中第k个任务vl,k的修竣时限dvl,k.

对于当前抢修组l，抢修任务的如期完成数量为Nl，则有

(2)

式中：w(l,k)用来标识分配给抢修组l的第k个抢修任务能否如期完成，如果完成时刻sl,k早于给定的时限dvl,k，则该任务能够如期完成，w(l,k)=1，反之w(l,k)=0.

若装备修竣时限视为硬约束，则每个抢修任务都应在修竣时限之前完成，即如期完成的装备数量应与分配的任务数量一致。为确保决策求解过程中得到可行解，这里用Ql标识任务完成状态，Ql=1表示抢修组l能按要求完成全部任务，Ql=0表示该组不能按要求完成全部任务，即

(3)

在修竣装备数量相同的情况下，装备越早修竣越好，这里以被修装备的修竣时刻与修竣时限之间的差值之和DLl作为对应的指标，DLl的计算公式为

(4)

从任务的角度，每个任务最多只能被执行一次，因此引入Xi,l表示作业点i抢修任务是否被赋予抢修组l，Xi,l=1表示抢修组l的任务中有作业点i抢修任务，Xi,l=0表示该组的任务中不包含作业点i抢修任务。

从决策角度，如期完成的任务数量越多越好，修复节约的总时间越长越好，根据决策者的决策偏好，可以将上述指标进行组合，建立相应的决策目标函数。

2.2 多抢修组条件下的抢修决策目标

抢修任务分配决策的目的是充分利用有限的时间和资源通过一次行动尽可能多地完成抢修任务。因此，一次行动能够如期完成的抢修任务数量是最重要的决策变量，当任务完成量相同时，被修装备的修竣时刻越早越好，即装备修竣时刻与装备修竣时限的时间差DL值越大越好。因此在给定V、P、D、E的前提下，综合上述两类决策指标构建决策目标函数：

(5)

式中：目标函数ObjV的第1部分为各抢修组选定任务数量之和，第2部分为装备修竣时刻与装备修竣时限的时间差DL与总修竣时限之比。当任务能够如期完成时，DL的总和应低于总修竣时限，因此第2部分取值区间为0～1，而每多完成一个任务，目标函数即增1，因此确保了任务完成量作为主要决策变量，DL作为决策变量主要用来在选定任务的基础上，对任务的执行顺序进行优化。因此从权重上看，修复任务数对目标函数影响较大，当修复数量相同时，总节约时间越长的越好。第1个约束条件表示每个抢修组所分配的任务能够全部如期完成；第2个约束条件表示每个待修任务只能唯一地分配一次，由一个抢修组进行抢修；第3个约束条件表示待修任务可以不分配。约束条件确保决策的解都是可行的，同时为任务分配和排序提供一定的寻优空间。

3 决策求解算法

上述决策问题属于奖金收集车辆路径问题(PCRVP)中的一类，目前已有启发式算法、禁忌搜索和多阶段算法等用于求解此类问题[11-13]。但该决策模型将任务完成数量和总节约时间作为目标函数，且将任务完成率作为约束条件，使模型具有一定的特殊性，因此设计遗传算法进行优化求解。

根据第2节确定的决策优化模型，模型的目标是在多抢修组、多任务的条件下，求得任务分配的组合及每个任务组的优先排序方案，求解空间维度极高，求解难度较高，为了降低计算难度，本文选择将遗传算法与随机遍历算法相结合，对任务组合和子任务排序进行联合求解[14]。求解思路如图2所示。

图2 决策求解过程Fig.2 Solving procedure of optimal decision-making

如图2所示，采用遗传算法进行决策寻优，对抢修任务进行随机分配和排序，并将对应的抢修方案通过编码表示为染色体，以2.2节提出的目标函数构建适应度函数，并进行迭代求解。由于受修竣时限的约束，染色体的随机交叉、变异会产生许多不可行解。因此在每代种群迭代后，对染色体进行整理，以确保在当前任务分组的前提下，抢修序列是相对较优的。

1)染色体编码方案。一个染色体应包含抢修方案的所有信息，即任务分配和排序。对于给定的Ntot个抢修任务和M个抢修组，按顺序将抢修任务进行唯一的数值编号，即染色体中数值为i的基因对应表示作业点i抢修任务，将所有任务编号随机排序，由于抢修出发点已经确定，即染色体首位皆为1；而后根据抢修组的数量和编号，确定染色体分段位置，并进行标识。分段标识数量与抢修组数量相同，且按照抢修组编号从小到大排列于染色体末尾，分段标识对应数值即为对应抢修组的任务队尾所处位置。假定当前共2个抢修组遂行6个抢修任务，图3示例所示即为一随机染色体。

图3 染色体编码示例Fig.3 Example of chromosome coding

图3中，染色体后两位为分段标识，其数值分别为3和5，表示1至3所列任务为第1抢修组的任务，4至5所列任务为第2抢修组的任务，第1抢修组按照{1,2,6}的顺序进行抢修，第2抢修组按照{4,5}的顺序进行抢修，任务3未列入抢修计划。

2)适应度函数。初始种群根据编码规则随机产生第1代个体，根据每个染色体的表现计算出适应度值，将第n个染色体对应适应度值记为Tn，将个体n的适应度定义为

(6)

(7)

式中：max(Tn)为本代个体的最大目标函数值；η为适应度系数，η取值越小，淘汰率越高，收敛速度越快，这里采用变适应度系数的策略，对η递减取值，以防止过早收敛，无法求得全局最优解。

3)选择算子。为确保寻优效率，采用轮盘赌策略进行种群迭代选择，然后进行染色体交叉和变异。

4)杂交和变异算子。由于染色体编号属于混合编码，因此染色体不应随机交叉。为了保证交叉后的染色体仍然对应可行解，采用整体交叉的方法，即被交叉的染色体中任务编码子段整体交叉，如图4所示。

图4 染色体交叉操作方法Fig.4 Crossing rule of chromosome

图4中，a和b都是2个抢修组、5个抢修任务条件下的待交叉染色体，交叉时对应将前6个位置的基因整体对调，即完成了染色体交叉。操作，按照{6，4，5}的顺序进行重新排序并插回原染色体，同样，在染色体a中找到染色体b中被选中的基因段，作相同操作，交叉前后的基因段则都能够对应决策可行解。

变异算子采用双位变异操作模式，在个体染色体中随机抽取2个基因位进行交换而产生新的个体。

5)整理染色体。在不改变给定任务分组的情况下，采用随机遍历方式调整任务的排序，以提高节约时间的长度。

6)进化策略。考虑到选择算子和交叉算子的迭代择优效率不高，为了保存进化成果，每一代经过选择、交叉和变异操作后都保留当代最优个体，剔除最差个体，以保证算法具有全局收敛性。

4 应用实例

假设在某次联合进攻战役过程中，我数字化合成部队与当面之敌展开攻防作战，在正面作战方向上，数字化合成部队所属两个合成营突破敌永久防御攻势向纵深发展，期间受敌地雷和反坦克武器的攻击，两营报告坦克和步兵战车共战损15台，受前方指挥所指示，某伴随保障队指挥2个抢修组，准备前出进行战场抢修。已知各战损装备的待修位置，前方抢修力量已经完成损伤的初步评估，预测得出各单装的现地抢修工时(见表1)，各作业点之间的距离换算为时间(见表2)，为了保证进攻的持续性，前方指挥所对各台装备的修竣时限提出了要求(见表3)。

表1 各作业点现地抢修耗时

目前部署地域准备前出完成抢修任务，需为各组明确任务和抢修顺序。

应用数学分析软件MATLAB编写遗传算法求解程序，进行决策优化求解，主要计算过程如下：

1)利用表1～表3中的数据建立机动时间矩阵、修复时间矩阵和修竣时限矩阵，设定遗传算法参数，随机生成初始种群。

2)根据(5)式计算初始种群中各个个体的适应度值。

3)根据设定的种群保留概率随机生成相应数量的子代个体，根据轮盘赌的策略选择父代个体生成新种群。

4)根据杂交概率进行交叉操作。

5)根据变异概率进行变异操作。

6)根据当次种群保留概率用当代最优个体替换最差个体。

7)更新群体，用新种群替代父代种群，更新种群保留概率。

8)判断是否达到最大遗传代数或代际适应度最优值变化量低于阈值，则算法终止，并输出最优结果；否则转第2步。

根据案例中决策问题的特点，设定遗传算法参数：群体规模为500，最大迭代次数为100，种群初始保留概率为0.95，杂交概率为0.7，变异概率为0.8.

表2 作业点之间的机动耗时

表3 各作业点修竣时限

按照上述参数进行决策求解，求解结果如图5所示，由图5可知，在约40次迭代后，最优解即收敛到相对最优值。

图5 决策优化求解结果Fig.5 Iterated output results of decision-making algorithm

最优的染色体为{1,6,8,13,12,4,2,15,9,7,5,10,14,16,11,3,5,10}，得到最佳的任务分配方案和抢修顺序为：第1抢修组{1,6,8,13,12,4}；第2抢修组{1,2,15,9,7}。按照该方案，抢修1组和2组分别能够如期完成5个和4个装备抢修任务。各抢修任务的具体修竣时间如表4所示。

表4 最优抢修方案抢修时序及修竣时刻

各任务的修竣时间和修竣时限的对比图如图6所示。

图6 任务修竣时间与修竣时限对比图Fig.6 Time-limit and estimated finishing time of selected spots

由上述方案可知，2个抢修组能够如期完成10个抢修任务，在给定的15个抢修任务中，仍有5个作业点无法如期完成抢修任务，若无其他抢修组可用，可组织相应装备后送。若有其他抢修组可用，可改变本案例中的相关参数，实施优化求解，得出最优的求解方案。

通过上述分析，可知本文提出的装备抢修任务分配决策方法能够有效地解决时间硬约束条件下装备伴随抢修任务的多组别分配问题，能够有效地提高装备抢修过程中的指挥决策效率。而且与简单的抢修优先排序和单抢修组路线寻优相比，本模型考虑了装备修竣时限的差异性以及多抢修组并行执行任务的现实需求，更符合作战需要和战场实际。

5 结论

本文主要以在规定时间内完成尽可能多的抢修任务为目标，在考虑多抢修组的条件下，对装备抢修任务的选择和分配问题开展研究，首先根据决策目标，确定了以任务完成数量为主，以时间消耗为辅的决策寻优目标，在抢修任务数量可变、抢修顺序可变的前提下确定了多抢修组抢修决策优化模型。针对决策求解难度大的问题，通过改进遗传算法，提出了可行的求解方法，并通过案例验证了求解方法的有效性。

由于战时装备抢修态势处于持续变化之中，一次抢修决策往往无法符合战场实际需求，在下一步的研究中，有必要针对抢修任务分配的动态决策展开研究，以充分考虑抢修组的能力变化和抢修任务的实时变化。