基于三维场景和图像边缘特征的浅浮雕建模

李婧雯 计忠平

(杭州电子科技大学计算机学院 浙江 杭州 310018)

0 引 言

浮雕作为一种雕刻艺术，可以根据不同的空间压缩程度分为高浮雕和浅浮雕。高浮雕在造型上更接近完整的3D模型，而浅浮雕是通过对其高度场进行压缩，将形状挤压到接近平坦的表面，同时又不失三维场景的感知，保持空间立体感，是一种介于二维平面和三维雕刻之间的独特艺术效果。浅浮雕的应用广泛，如图1所示，可以从历史中轻易找到大量的浅浮雕艺术品。时至今日，浅浮雕在硬币、工业设计和建筑等多种行业中应用广泛。

图1 浅浮雕应用

传统的浮雕制作依靠老艺术家的手艺，不仅耗时费力，对艺术家的技术要求十分严格，一旦出错就前功尽弃。随着数字信息技术的发展和3D打印技术的普及，数字浮雕和传统浮雕相比，其易生成且容易再次编辑修改，可以用来批量生产，大大提高了浅浮雕的制作效率和精度，降低了制作成本。

1 相关工作

近年来，涌现出大量的数字浅浮雕研究工作，主要分为三类：基于图像、基于高度场、基于法线。基于图像的浅浮雕生成方法主要利用特征提取、三维重建等技术从二维图像生成三维浅浮雕。吴文明等[1]将图像的灰度值作为初始高度场通过光滑处理得到初始浅浮雕，再融合图像细节增强的部分，最终得到保细节特征的浅浮雕。Wu等[2]将2D线型笔画与法线笔画相结合，提出一种由单幅图像交互式构建高度场的方法。Sohn[3]提出使用智能手机生成浅浮雕的算法，用智能手机拍摄照片得到原始图像，利用原始图像、梯度图像和深度图组合生成浅浮雕表面，并使用三个参数控制浅浮雕的细节纹理。虽然二维图像的方法对输入要求降低，但是单幅图像的信息不充分，很难获取绝对的深度信息，无法得到唯一的高度信息。而基于高度场的浅浮雕设计的基本方法是对空间中给定观察视点的3D几何模型，获取其深度值然后进行压缩来获得最终的浅浮雕。Cignoni等[4]首次分析了浅浮雕的几何属性，基于图形透视转换关系将3D场景转换成高度场，然后直接对高度值进行缩放得到浅浮雕。Song等[5]在微分坐标中表示3D形状，然后结合网格的显著性使用非锐化遮罩和平滑技术来生成浅浮雕，但是该方法没有增强轮廓特征。Kerber等[6]借鉴了Lee等[7]的思想，结合线性重缩放和梯度域增强技术，通过四个参数控制深度压缩比例和物体表面的细节信息。Weyrich等[8]为了改善深度值不连续的问题，从HDR图像的压缩算法中得到灵感，在梯度域通过参数控制边缘轮廓的检测，再非线性地压缩梯度值，最终得到浅浮雕。Kerber等[9]通过采用双线性滤波技术和非线性压缩的方法，解决在压缩的过程中三维模型表面精细特征丢失的问题，用户通过指定压缩比来控制最终的浅浮雕高度。Bian等[10]使用拉普拉斯坐标存储细节特征，并提出一种新的基于反正切的压缩函数，最后依赖阈值来精确调整浅浮雕高度。由于在图像空间生成浅浮雕耗费时性，文献[11-13]通过微分网格形变和双边滤波技术来实现对浅浮雕的实时建模，并保留浅浮雕的细节特征。Zhang等[14]考虑光照对浅浮雕外形的影响，提出了一种根据给定的照明方向、材料和模型厚度自适应生成浅浮雕的新方法。Wei等[15]基于法线的网格处理，解决了离散几何处理中的浅浮雕建模问题，使用三个参数控制最终浅浮雕的细节、高度和样式，使得最终的浅浮雕在具有高压缩比的情况下更好地保留了几何细节和整体形状。Nie[16]首次提出基于点云数据，采用改进的Z-Buffer算法和双线性插值分两步生成浅浮雕，并使用多个参数控制浅浮雕的压缩方案，该方法新颖，但是只适用于干净、均匀采样的点云。相较于前两种方式，基于三维模型的方法是近年来研究的热点，已经有很多学者取得了不错的进展。还有一些研究者在产生的浮雕基础上进行编辑和风格化，如Ji等[17]提出一种基于法向域编辑的浅浮雕风格化设计，通过对法向域分频处理，得到风格迥异的浅浮雕模型。基于深度场的浅浮雕建模方法目前的研究核心是如何最大限度的保留细节特征以及他的连续性、层次感、平面约束等。根据研究发现此前的大部分浅浮雕算法对参数有很强的依赖性，不同的场景往往需要选择不同的参数，参数选择得不好将导致细节丢失或高度不连续无法去除，因此需要设计一个更加智能的算法以自动地生成浅浮雕模型。

本文将结合图像和深度场两种方法研究如何自动生成浅浮雕，首次提出基于边缘概率场的自适应非线性压缩，并且在不需要人为输入参数的情况下能控制浅浮雕的细节层次。

2 算 法

2.1 边缘检测

首先输入高度场，将高度场转换为高度图，再对高度图进行边缘检测。本文提出基于结构化随机决策森林[18]对三维场景的高度场进行边缘检测。利用局部图像结构化的优点，将一幅完整的三通道图像分割成n份图像块，用决策树对结构化的图像块进行分类，再将多棵决策树结果进行融合得到最后的边缘图。

2.1.1训练决策树

给定一棵决策树ft(p)，每个节点通过一个二元分裂函数，向左向右分支，直到叶子节点，从而对样本p∈P进行分类。定义一个分裂函数：

ψ(p,θ)={0,1}

(1)

当ψ(p,θ)=0时，将p分给左边，否则分给右边，直到叶子节点结束。一个很有效的方法是将p的单个特征维度与阈值进行比较：

θ=(k,τ)ψ(p,θ)=[p(k)<τ]

(2)

这里我们定义一个信息增益标准：

(3)

训练时，对每棵树的训练结果或者对每个节点的数据进行随机采样。在节点注入随机性会产生更高的精度，这种牺牲单棵树精度的方法会提升整体结果的多样化。

2.1.2结构化随机森林

本节描述如何对高维度复杂的结构化标签进行训练。首先将每个局部图像p∈P的结构化标签q∈Q映射到离散标签c∈C:

∏:Q→C

结构化标签是高维度且复杂的，如果对应每个标签q分别计算c，会很浪费时间和空间。为了降低计算的复杂性，使用中间映射:

∏:Q→Z

先计算空间Z的欧氏距离来计算结构标签q的相似性，降低Z的维数。为了使Z的维度更低，对空间Z的m维进行采样，得到子映射空间z，采样Z为学习中注入了额外的随机性，保证了树的结果的多样性。最后使用主成分分析法进一步对离散空间Z进行降维。

再使用K均值聚类算法将Z映射到空间C中，将Z空间分成K个聚类。使得相似z的结构标签q分配给相同的离散标签c。然后使用Shannon熵或基尼指数计算c中的信息增益来近似结构标签q的信息增益。再利用2.1.1节的训练过程来学习结构化随机森林。

2.1.3集合模型

随机森林将多棵决策树的输出进行集成获得结果，而如何融合不同决策树的预测，会对最终结果产生很大的影响。常见的随机森林的集合方法有投票和平均。本文定义一个将结构化标签(q1,q2，…，qn)组合成一个单一预测的方法。和前面一样，采样一个m维的映射z，计算每个结构标签qi的欧氏距离zi，选择zk对应的标签qk，其中zk是到所有zi的距离之和最小：

(4)

对于重叠的边缘映射，可以通过对多个重叠的边缘映射求平均的方法，得到一个软边缘响应。

2.1.4深度图边缘检测

由于获取的深度图整体亮度偏暗，对比度不明显，故使用限制对比度的自适应直方图均衡化(CLAHE)的方法对图像亮度进行调整。直方图均衡化的灰度映射公式为：

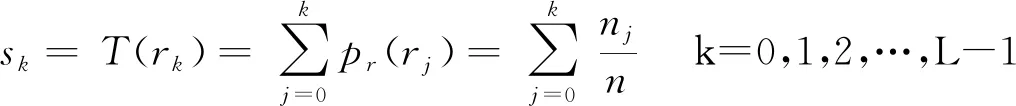
(5)

式中：sk是均衡化后第k级灰度；rk是原图的第k级灰度，表示原pr(rj)图rk出现的概率；nj是原图灰度级为rk的个数；n为原图像素总数。子块的个数num会影响均衡化的效果，均衡化的结果会对后面浅浮雕的生成产生影响。图2所示为不同num的值处理后的深度图。

(a) 初始深度图 (b) num=10的边缘图(c) num=16的边缘图

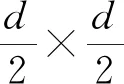
2.2 深度压缩

Cignoni等[19]认为保留浅浮雕平面特征是最重要的目标，但是过多的平面约束会导致深度压缩后的模型变型。为了满足其他约束条件，如轮廓的连续性，高度场必须按比例缩小到一定程度使场景的重要特征不被丢失。本文方法是基于边缘概率的压缩方法，放低对平面的约束，保留深度不连续处的轮廓。

2) 梯度压缩。Weyrich等[8]设置一个阈值来检测轮廓，并将轮廓处梯度置为0，只压缩非轮廓的梯度域。这里首次提出一种压缩方案：把2.1.4节得到的轮廓域视为控制压缩程度的概率场p(x,y)，希望在加大轮廓域的压缩程度的同时衰减非轮廓域的压缩程度，定义了一个自适应压缩函数根据概率场值进行自适应的压缩梯度域。由于线性压缩会导致浅浮雕过于平坦，为了保持平坦的同时又保留细节特征，最终定义一个自适应非线性压缩函数：

c(x)=γlog(1+γ×x)

(6)

式中：γ=1-p控制不同区域高度的压缩程度，取值范围为(0,1]，值越大对应的压缩程度也越大。通过对梯度域的压缩最终得到修正后的梯度模值：

(7)

2.3 重建高度场

理论上最后的一步是对前面修正后的梯度域g′(x,y)进行积分，恢复浅浮雕最后的高度场，将修正后的梯度域和方向重新组合：

g′(x,y)=s(x,y)v(x,y)

(8)

但是实际上修正后的梯度域不再可积，可以通过将最优化方法重新表述成泊松方程来得到最后的高度场。泊松方程为：

(9)

先对修改后的梯度场g′进行下采样，再求其拉普拉斯算子。对于大型稀疏矩阵，通过使用一个网格求解器对式(9)进行求解。

3 实 验

本文算法的详细流程如图3所示，展示了原始高度图通过边缘检测、自适应非线性压缩梯度域以及最后的重建，得到最终的浅浮雕模型。

图3 基于边缘检测的浅浮雕建模

1) 使用CLAHE方法处理后对边缘检测结果的影响。由于深度图的灰度对比不明显，所以直接检测的结果不理想，初始高度图提高了灰度对比度后再进行检测。图4为CLAHE中的分块参数num对边缘检测结果的影响。图5为不同边缘检测结果对浅浮雕产生的影响，随着轮廓特征增多，浅浮雕的细节特征越来越明显，也保证了高度的连续性。

(a) 初始深度图 (b) num=10的边缘图(c) num=16的边缘图

(a) 初始边缘图对应的浅浮雕 (b) num=10对应的浅浮雕 (c) num=16对应的浅浮雕

2) 梯度域边缘处理的压缩程度对浅浮雕风格的影响。如图6所示，如果对整个梯度域同等程度压缩，得到的浅浮雕的轮廓处出现台阶，而自适应的压缩函数根据不同区域进行不同程度的压缩后，轮廓处避免了这种现象。

(a) 边缘未处理 (b) 边缘处理

3) 与已有的工作成果对比。文献[8]方法属于半自动生成浅浮雕，需要手动设置参数进行检测才能得到细节增强的浅浮雕，而本文方法通过全自动的无参检测就能得到同样效果的浅浮雕。如图7所示，文献[8]方法需要根据三维场景的不同来设置不同的参数，θ是控制边缘检测的阈值；而本文方法参数一致就能产生同样理想效果的浅浮雕。

(a) 文献[8]方法例一θ=0.008 (b) 文献[8]方法例二θ=0.001 6 (c) 文献[8]方法例三θ=0.005

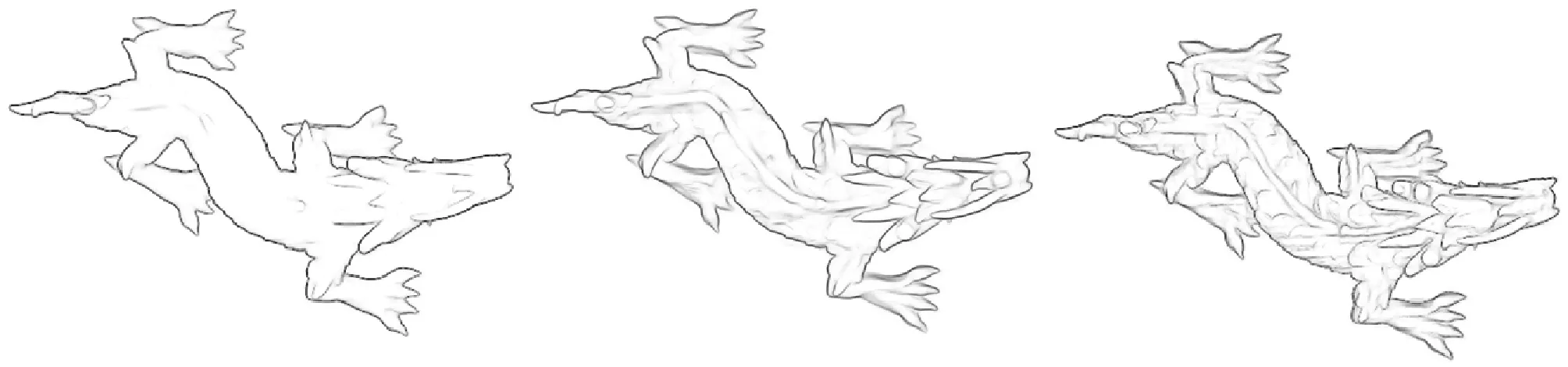
本文方法和文献[17]方法的对比结果如图8所示。文献[17]方法不需要参数，产生的浅浮雕平坦且平滑；本文算法产生的浅浮雕保持高度的连续性的同时更加立体，而且轮廓处细节更加明显。但是文献[17]方法对非流形的三维场量不可行，如图8(e)所示，该方法无法获得正确的法向图，而本文方法却可以产生效果很好的浅浮雕，证明本文方法适用性更广。

图8 本文算法与文献[17]方法的对比

4) 验证本文算法的优势。首先验证本文全自动生成浅浮雕算法对所有模型的普适性。图9所示为一系列不同类型的深度场用本文算法生成的高质量的浅浮雕模型。然后比较不同算法的时间性能，如表1所示。本文算法在边缘检测阶段的时间只需几秒，而高度场重建的时间和对比方法差不多。虽然本文算法的运行时间多了2～3秒，但是有利于浅浮雕的自动生成和效果控制。

(a) 浅浮雕例一 (b) 浅浮雕例二 (c) 浅浮雕例三

表1 不同方法的对比例子运行时间

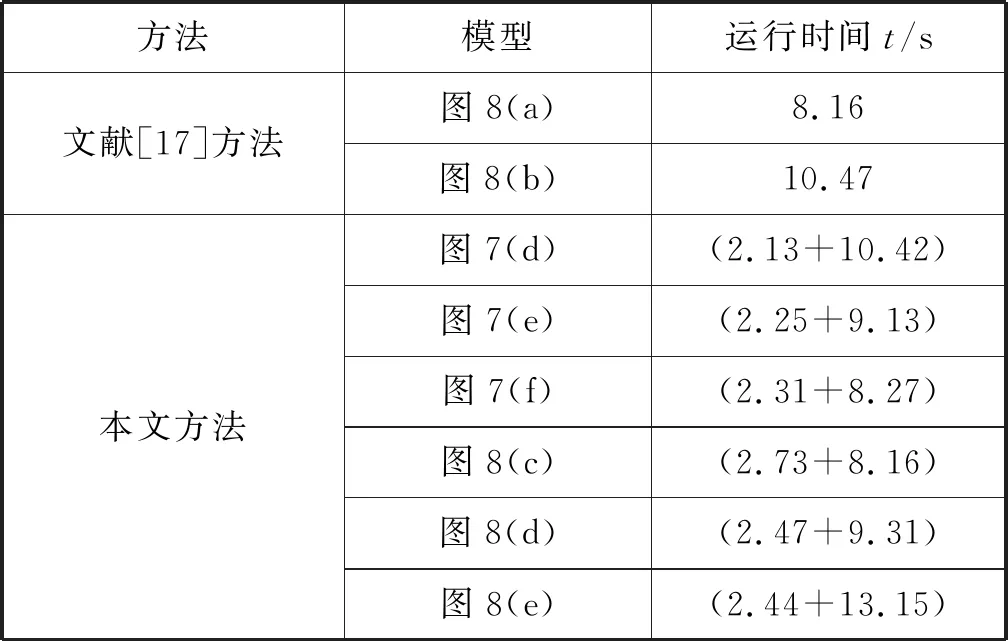
续表1

5) 本文算法的运行环境。实验的计算机的配置如下：十六核3.7 GHz AMD 2700X处理器，16 GB内存，Windows 10 64位操作系统，使用MATLAB编程实现。

4 结 语

本文针对原有的单一的基于图像和3D模型的浅浮雕建模方法，提出一种结合3D场景和图像处理的浅浮雕建模算法。本文创建一个浅浮雕建模系统，输入一个三维场景，获取其深度图，对其进行边缘检测，再根据边缘图的信息对深度图的梯度进行调整，最后以最小二乘法计算得到逼近修改后梯度场的浅浮雕模型。由于边缘检测自动识别处理了深度图中深度值的不连续性，本文方法不需要人为选择参数，因此方便了浅浮雕的建模，也提供了机制用于控制边缘图的细节层次，可以增加浅浮雕的细节层次效果。未来工作主要包括两个方面：采用更高效的边缘检测算法；针对局部细节进一步优化，如增强、风格迁移等，得到类型更加丰富的浅浮雕模型。