基于高斯似然估计因子分析的点云配准算法

李 灿 孙 未 张力云

(成都理工大学核技术与自动化工程学院 四川 成都 610059)

0 引 言

点云配准技术是一种重要的数字检测技术，现已蓬勃发展并广泛运用于各个行业，如计算机视觉、高精度加工、无损检测、虚拟现实等[1-4]。通过三维扫描仪对物体表面进行多角度扫描，得到不同视角下的三维点云数据，再将所得的点云数据进行配准，即可得到完整的模型。Besl等[5]提出的最近点迭代(Iterative Closest Point,ICP)算法广泛运用于点云配准中，作为经典的配准算法，其主要手段是通过寻找两个点集的对应点，并计算其变换矩阵，但该算法容易陷入局部最小值并且效率不高[6-7]。

由于ICP算法存在的部分缺陷，众多学者都提出了各种各样的改进算法来减小配准误差和提高配准效率。Bae[8]提出基于曲率和法向变化率的几何基本最近点迭代(GP-ICP)算法，该算法使得ICP算法对迭代初始值的要求降低。Ying等[9]提出基于七维空间迭代的Scale-ICP算法，虽然其收敛速度较快，但对迭代过程非常依赖且仅能应用于点云整体存在相似变换的情况。Sharp等[10]提出的最近点迭代(ICPIF)算法主要利用不变特征配准，该算法可实现局部重叠的点云配准，但是在理论上对点云数据缺失情况下的配准很难实现。

本文提出一种基于高斯似然估计因子分析的点云配准算法。将点云配准的数学公式模型扩展为因子分析模型，这样便将点云配准转化为对因子模型参数的求解；采用多元高斯函数对点云数据进行逼近，并通过EM算法求解出因子载荷矩阵，再利用所求得的因子载荷矩阵完成对点云的配准。实验表明，与其他几种算法相比，即使在点云无序、数据存在遮挡、缺失不完整，以及噪声环境下，本文算法仍可实现快速精确配准，收敛速度快，具有良好的鲁棒性。

1 基本原理

1.1 因子分析

一组D维的观测数据X={x1,x2,…,xN}的正交因子模型为：

(1)

(2)

通过上述正交因子数学模型可知，观测数据X的协方差矩阵为：

∑=AAT+φ

(3)

式中：φ为特殊因子矩阵ε的协方差。

1.2 点云配准原理

将源点云P={p1,p2,…,pn}和目标点云Q={q1,q2,…,qm}进行刚性几何变换：

pi=Rqj+ti=1,2,…,n;j=1,2,…,m

(4)

式中：R∈R3×3为旋转矩阵,且RTR=I；t∈R3×1为平移向量。由式(3)可知，两点云的协方差矩阵可表示为:

由式(4)可得到两点云协方差矩阵的关系为：

∑P=R∑QRT

(5)

点云数据在实际运用中可能会有噪声干扰，可以通过正交因子模型对数据处理，计算出两点云的因子载荷矩阵，可以将特殊因子协方差矩阵看作是噪声项。所以降噪后的点云协方差矩阵为：

(6)

ΛP=ΛQ

(7)

综上所述，可得：

(8)

为了计算出平移向量t需要先计算出点云P和点云Q的均值点，即：

(9)

进一步得到：

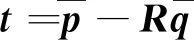
(10)

2 参数求解

2.1 极大似然估计

对样本X={x1,x2,…,xN}进行极大似然估计：

(11)

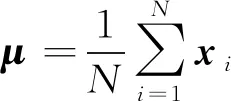
2.2 EM迭代

为了求解2.1节的最大值，这里采用最大期望算法(Expectation Maximization Algorithm，EM)对上述问题进行求解，EM算法分为两个部分。E步：计算完整数据的对数似然函数的期望；M步：通过将中间量最大化的值来获得新的参数值。

由2.1节可知为了估算旋转矩阵，需要求解的参数为AP、AQ、φP、φQ，在EM算法下需要计算每个观测值的概率属性γi，同样为了计算γi需要假设一个中间隐藏变量fi，计算结束之后可消掉。则代价函数为：

(12)

式中：θ={μ,A,φ}表示待求解参数；fi是第i个中间隐藏变量且f～N(O,I)；γi(fi)是第i个中间隐藏变量的观测值。E步，计算γi(fi)，由高斯边缘分布条件可得X和z的联合分布为：

(13)

因此，有：

(14)

根据多元高斯分布公式，得到：

(15)

M步,将代价函数进一步表示为：

(16)

对A求偏导：

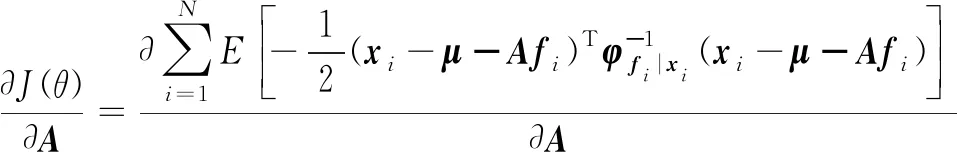
(17)

令式(17)等于0，可得：

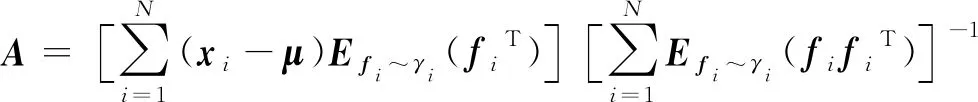
(18)

由式(13)可知：

(19)

综上所述：

(20)

求解过程中μ值不变。同理，用此方法对φ求偏导，省略推导过程，得到推导结果：

A(μfi|xi(μfi|xi)T+∑fi|xi)AT]

(21)

本文算法流程如图1所示。

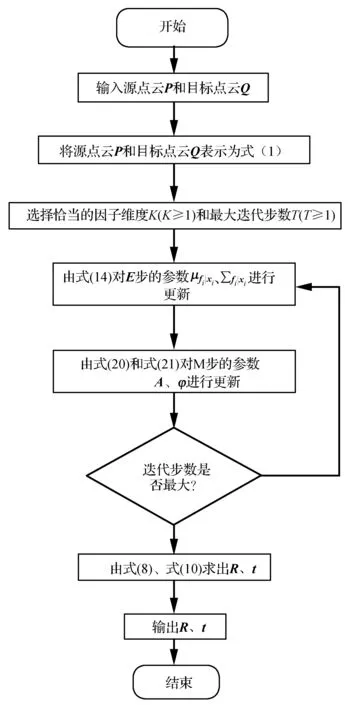
图1 本文算法流程

本文算法是在MATLAB 2017a版本下实现的，具体步骤如下：

Step1通过式(1)将点云P和点云Q表示为正交因子模型。

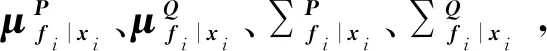
%E步：

for i=1:N

muf(:,i)=A′/(A*A′+phi)*(X(:,i)-mu);

%更新每一个中间均值变量muf

Ef(:,:,i)=eye(K)-A′/(A*A′+phi)*A;

%更新每一个中间协方差变量Ef

end

Step3由式(20)分别更新点云P和点云Q的正交因子载荷矩阵AP、AQ和残差矩阵φP、φQ,具体代码如下：

%M步：

%更新A

A1=zeros(D,K);

%初始化中间变量矩阵为D×K的矩阵

A2=zeros(K,K);

%初始化中间变量矩阵为K×K的矩阵

for i=1:N

A1=A1+(X(:,i)-mu)*muf(:,i)′;

%计算(X(:,i)-mu)*muf(:,i)′的累加和A1

A2=A2+muf(:,i)*muf(:,i)′+Ef(:,:,i);

%计算muf(:,i)*muf(:,i)′+Ef(:,:,i)的累加和A2

end

A=A1/A2;

%利用累加和A1和A2更新因子载荷矩阵A更新phi

P=zeros(D,D);

%中间残差矩阵初始化为D×D的矩阵

for i=1:N

P=P+X(:,i)*X(:,i)′-X(:,i)*muf(:,i)′*

A′-A*muf(:,i)*X(:,i)′+A*(muf(:,i)*muf(:,i)′+

Ef(:,:,i))*A′;

%采用累加和的方式更新中间残差矩阵P

end

phi=diag(P/N);%取1/N倍中间残差矩阵的对角线元素

%得到1×D的向量

phi=diag(phi);%将1×D的向量转化为对角线残差矩阵，

%完成对对角线残差矩阵phi的更新

Step4重复Step2和Step3直至收敛，由式(6)-式(8)利用AP、AQ估算旋转矩阵R。

Step6由式(10)估算出平移向量t。

3 实验与仿真分析

仿真主要是通过对来自斯坦福大学的公开点云数据Bunny(分辨率：31 607个点)和Horse(分辨率：48 485个点)三维点云数据进行仿真配准，和对来自三维激光扫描仪HandySCAN 700分别从正面与侧面对现场实际物体进行扫描的实验数据进行配准，噪声为高斯白噪声。三维激光扫描仪HandySCAN 700配置参数如下：

产品用途：行业扫描

扫描元件：CCD

产品类型为3D扫描仪

扫描范围：自由扫描为0.1～4.0 m

扫描速度：480 000次测量/秒

产品尺寸：122×77×294 mm

产品重量：0.85 kg

使用条件如下：

电源类型：100～220 V

工作温度：5℃～40℃

工作湿度：10%～90%

使用方式：手持

激光类别：2级

精度：最高0.03 mm

实验预仿真环境为：MATLAB 2017a版本、i7-6700HQ四核处理器和GTX965M。为了确保配准精度，实验与仿真是在不能受到有其他软件的影响的条件下进行的。

3.1 经典配准

通过对Bunny和Horse点云的随机旋转和平移得到目标点云，然后对Bunny目标点云做随机丢失25%处理，对Horse的目标点云添加50 dB的高斯白噪声。点云初始状态如图2所示。

图2 Bunny和Horse点云的初始状态

分别利用本文算法、CPD算法、Go-ICP算法对三维点云数据配准，比较三种算法的配准精度和时间，配准效果如图3所示。

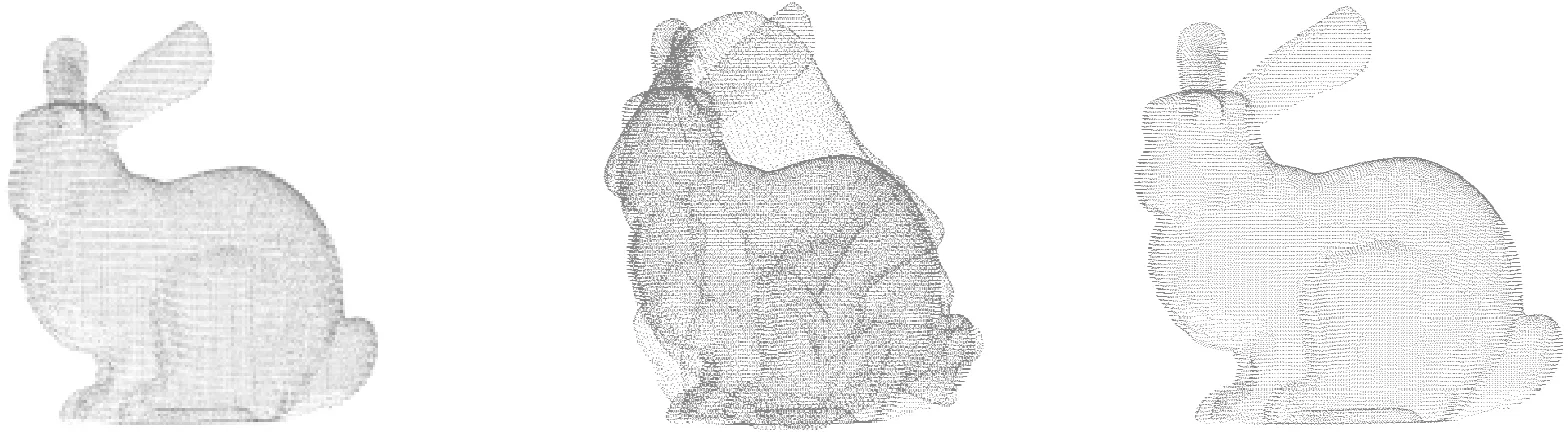
图3 三种算法对Bunny和Horse点云的配准效果

三种算法配准精度和配准时间如表1所示。

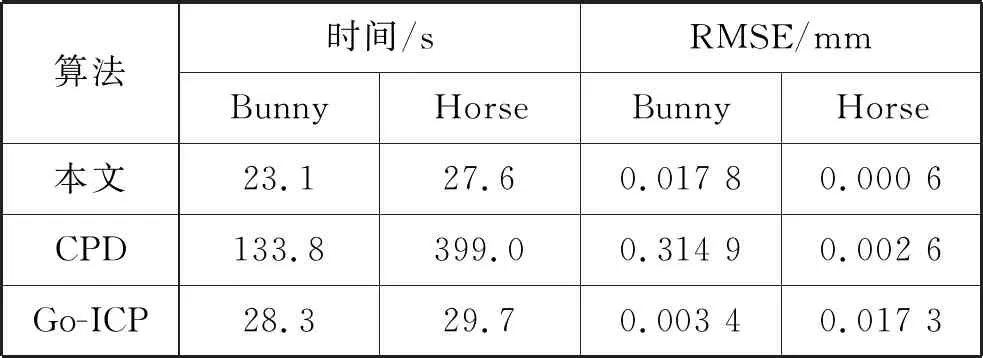
表1 三种算法的配准时间和配准误差

由图3和表1可知，CPD算法对Bunny和Horse点云配准在时间上明显多于本文算法和Go-ICP算法。在配准精度方面，本文算法对Bunny的配准误差要略大于Go-ICP算法，但对Horse的配准精度更优于其他两种算法。

3.2 实物配准

为证明本文算法具有实用性，采用三维激光扫描仪HandySCAN 700分别从正面与侧面对两组物体进行扫描，从正面与侧面分别扫描的目的是为了得到不同视觉下的点云数据集。得到Bottle和Banana点云的初始状态，如图4所示。其中：Bottle源点云(右)分辨率为21 450个点，目标点云(左)分辨率为21 430 个点；Banana源点云(左)分辨率为45 271个点，目标点云(右)分辨率为46 370 个点。

(a) Bottle (b) Banana

将本文算法与CPD算法和Go-ICP算法的配准效果进行对比，结果如图5所示。

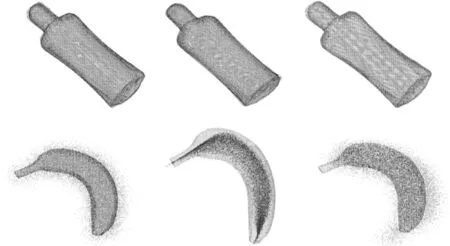
(a) (b) (c)

三种算法对Bottle和Banana点云的配准时间和配准误差如表2所示。

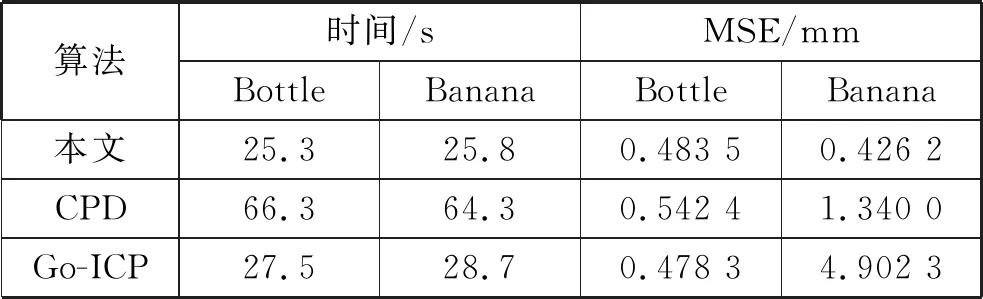
表2 三种算法对Bottle和Banana点云的配准误差和时间

实验结果表明，对Bottle和Banana进行点云配准时，本文算法所需的时间明显少于CPD和Go-ICP两种算法。三种算法在对Bottle进行点云配准时的配准误差相差甚微，但本文算法对Banana配准时的误差要明显小于其他两种算法的精度。

3.3 现场扫描机械点云配准

为充分验证本文算法对实物扫描数据进行配准的有效性,用便携式激光扫描仪 (HandySCAN 700TM) 对现场机械器件从正面与侧面分别进行扫描，从正面与侧面分别扫描的目的是为了得到不同视觉下的机械点云数据集，进行实物数据采集，然后对扫描数据做相应处理后，再进行配准。机械器件目标点云(右)分辨率28 437个点，和待配准点云(左)分辨率21 328个点，初始状态如图6所示。

图6 机械器件的初始状态

将本文算法与CPD算法和Go-ICP算法分别配准，配准效果如图7所示。

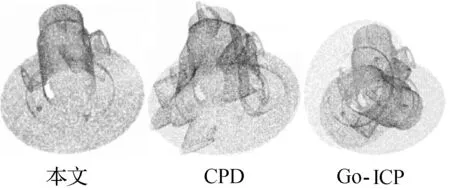
图7 配准效果图

三种算法的配准时间和精度如表3所示。

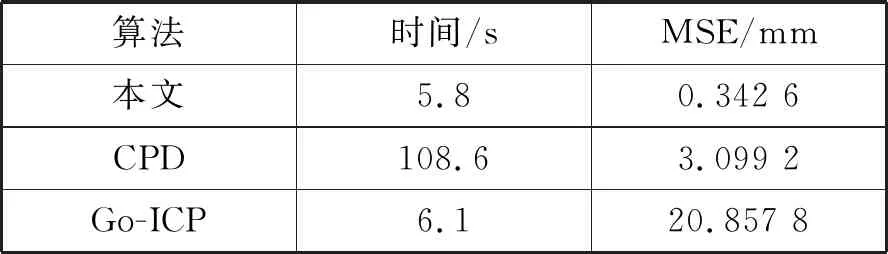
表3 三种算法的配准时间和配准误差

由图6和表3可知，对机械器件进行点云配准时，本文算法在配准时间上与Go-ICP算法相差甚微且远优于CPD算法，但在配准精度方面，本文算法明显优于其他两种算法。

综合分析发现，本文算法具有较好的实用性。该算法的应用前景主要是在历史文物保护、工程测量、医学图像重建等方面。

4 结 语

本文针对数据存在白噪声、数据缺失、无序，以及仿射情况下的三维点云提出一种基于主成分因子法的点云配准算法。将带白噪声的点云数学模型扩展为正交因子模型，从而将点云配准问题转化为对模型参数的求解；通过运用极大似然法得到因子载荷矩阵，进一步精确化模型参数，从而实现点云配准。实验表明，本文算法有效提升了配准精度和效率；与Go-ICP和CPD两种算法对比，本文算法的稳定性较高。