利用“K字型”模型求点坐标
王春龙


一、“K字型”模型再认识
如图1,点B、E、C三点在同一条直线上,AB⊥BE,DC⊥CE,AE⊥ED,易证△ABE-△ECD。只要两个三角形的相似比及其中一个三角形的一边长已知,就可求出三角形所有边的长。
若将此图形置于平面直角坐标系中,且点E坐标已知(定点),那么通过相似求得EC、CD后,即可通过平移点E的坐标求得点D的坐标。
一般情况下,两个三角形的相似比不会直接给出,如图2,连接AD,若∠DAE是一个大小确定的角(定角),则根据tan∠DAE=DE/AE=k就可以确定△ECD和△ABE的相似比。如果AE和点E的坐标也已知,那么类比图1的方法也可求得点D的坐标。
因此,我们可以利用这个模型求点D的坐标。如果题目只告诉我们∠DAE的大小和该角一边上的点E的坐标,那么我们需要构造如图2这样的“K字型”解决问题。
模型建立:如图3,当一角确定(角度或该角的三角函数值确定)时,在该角的一边(由两个定点组成的边)上找到一已知坐标的点(除角的顶点外的另一个定点),过已知点作垂线与角的另一边相交,可构造直角三角形(这个直角三角形的形状和大小是确定的),然后过直角顶点所在直线构造“K字型”即可确定点D的坐标
二、利用“K字型”模型求点坐标
例1 (2019·江苏常州二模)已知,如图4,二次函数y=-x2+2x+3的图像与x轴交于点A、B,与y轴交于点C,点D为该抛物线的顶点,点E(2,3)是抛物线上一点,连接AD、AE。若在该抛物线上有一点M,使得∠DA E=∠MCB。(1)略;(2)略;(3)求点M的坐标。
【分析】由(1)(2)的求解可知tan ∠DA E=1/3;第(3)问因为∠DA E=∠MCB,所以∠MCB是一个定角,又因为BC是一条定边,所以可套用模型,过定边BC上的点B作BF⊥BC,交CM的延长线于点F,然后以直角顶点B所在直线构造“K字型”求解。
【略解】分类讨论:①若M在BC上方(如图5)时,∠M1 CB=∠DAE,作BF⊥BC交CM1的延长线于点F,过点F作FG⊥BG于点Go由△COB-△BGF得BG=FG=1。由B(3,0)平移得F(4,1),所以直线CF的表达式为y=- 1/2x+3,得交点M1(5/2,7/4)。②若M在BC下方(如图6)时,∠M2CB=∠DAE,作BF⊥BC交CM2于点、F,作FH⊥BH,CQ⊥BQ,垂足为H、Q。同理可得M2(4,-5)。
【点评】过定角一边上的定点作垂线构造直角三角形是正确建立“K字型”模型的关键步骤。
例2 (2020·江苏常州二模)已知二次函数y=ax2+bx+6的图像开口向下(如图7),与x轴交于点A(-6,0)和点B(2,0),与y轴交于点C。(1)略;(2)略;(3)如图8,该函数图像的顶点为D,在该函数图像上是否存在点E,使得∠EAB=2∠DA C?若存在,請直接写出点E的坐标;若不存在,请说明理由。
【分析】要使得∠EAB=2∠DAC,就要先确定∠EAB的大小。可以通过作点D关于AC的对称点构造2倍角,然后构造Rt△DHA确定tan∠DAH的大小。当∠EAB大小确定,在∠EAB的一边AB上过定点B作垂线即可解决问题。
【略解】作点D关于AC的对称点D'(如图9),连接AD',作DH⊥AD'于点H。计算发现△DAC是一个直角三角形,然后在Rt△DAH中可得tan ∠DAH=3/4。由于∠EAB=2∠DAC,∠DA H=2∠DAC,所以∠EAB=∠DAH。分类讨论(如图10):①过点B作BF⊥AB交AE1于点F,易得F(2,6),直线AF的表达式为Y=3/4x+9/2,得交点E1(1/2,39/8);②过点B作BG⊥AB交AE2于点G,同理可得E2(7/2,-57/8)。
【点评】由于定角的一边在坐标轴上,所以此题的“K字型”模型简化成了一个直角三角形。此题求解的关键是构造得到2∠DAC的角,然后∠EAB才能符合模型中的定角原则。
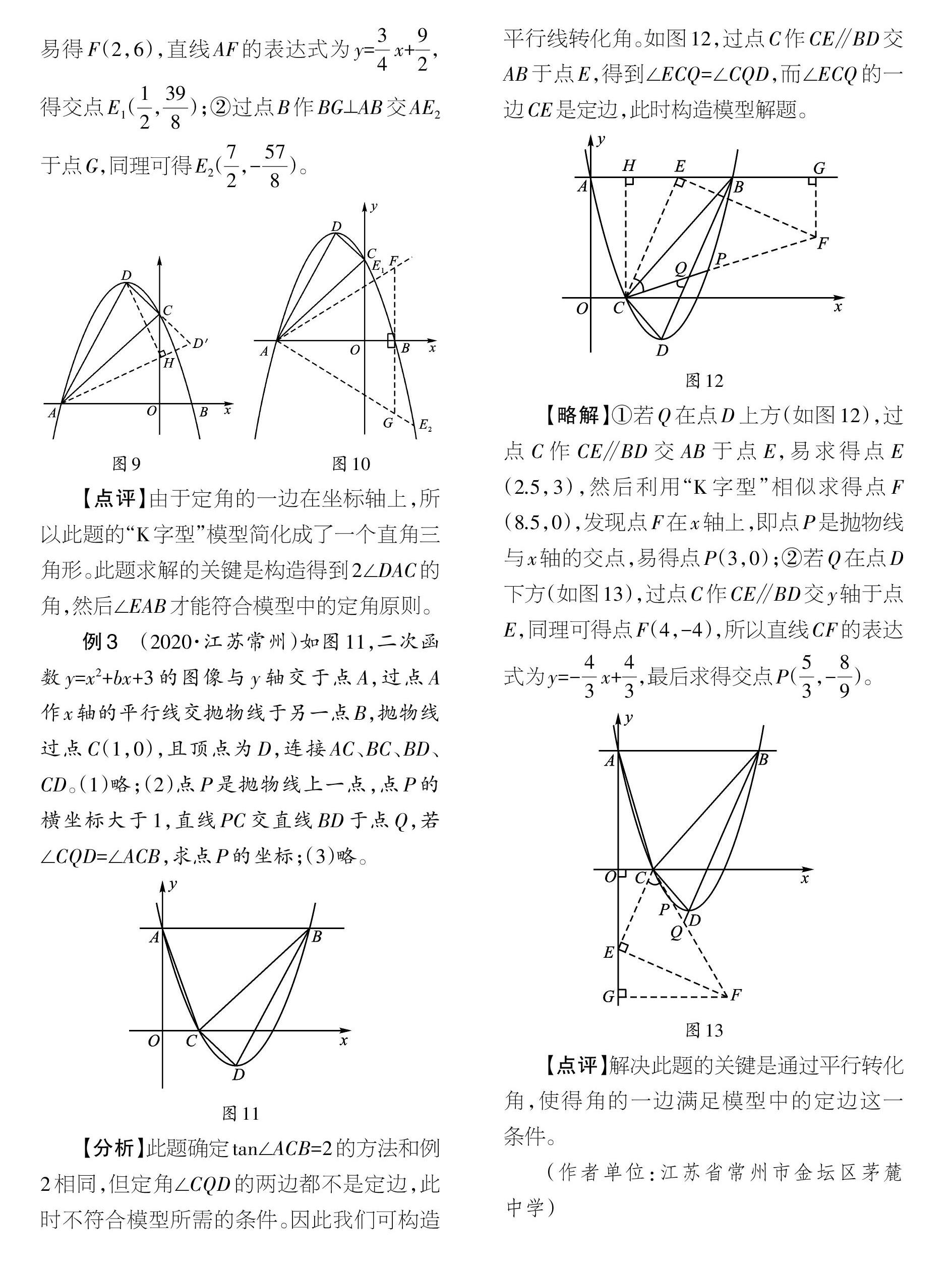
例3 (2020·江苏常州)如图11,二次函数y=x2+bx+3的图像与y轴交于点A,过点A作x轴的平行线交抛物线于另一点B,抛物线过点C(l,0),且顶点为D,连接AC、BC、BD、CD。(1)略;(2)点P是抛物线上一点,点P的横坐标大于1,直线PC交直线BD于点Q,若∠CQD=∠ACB,求点P的坐标;(3)略。
【分析】此题确定tan ∠ACB=2的方法和例2相同,但定角∠CQD的两边都不是定边,此时不符合模型所需的条件。因此我们可构造平行线转化角。如图12,过点C作CE∥BD交AB于点E,得到∠ECQ=∠CQD,而∠ECQ的一边CE是定边,此时构造模型解题。
【略解】①若Q在点D上方(如图12),过点C作CE∥BD交AB于点E,易求得点E( 2.5,3),然后利用“K字型”相似求得点F( 8.5,0),发现点F在x轴上,即点P是抛物线与x轴的交点,易得点P(3,O);②若Q在点D下方(如图13),过点C作CE∥BD交y轴于点E,同理可得点F(4,-4),所以直线CF的表达式为y=一4/3x+4/3,最后求得交点P(5/3,-8/9)。
【点评】解决此题的关键是通过平行转化角,使得角的一边满足模型中的定边这一条件。
(作者单位:江苏省常州市金坛区茅麓中学)

