单摆测重力加速度实验的改进

刘彧奇，谭雨莎，韦先涛，张 权，赵 伟，朱 玲

(1.中国科学技术大学 地球和空间科学学院，安徽 合肥 230026；2.中国科学技术大学 物理学院，安徽 合肥 230026)

单摆实验是一个非常经典的物理实验，根据摆的等时性原理制造的机械钟将人类的计时精度提高了近100倍[1-2]. 在用单摆测量重力加速度实验中，由于摆长不易准确测得，导致重力加速度的测量精度无法做到很高，一般只能达到1%左右.

本实验希望通过对实验方法进行改进，将直接测量单摆摆长改进为测量摆长的改变量，提高长度的测量精度；通过拟合摆长改变量(ΔL)与单摆周期平方(T2)之间的线性关系，获得重力加速度，并探讨改进摆线材料、测量方法、计算方法，使实验误差进一步减小，实际的实验误差可控制在0.1%以内.

1 实验部分

1.1 实验器材

在传统单摆实验装置的基础上，添加了游标卡尺和光电门，分别测量单摆摆长的改变量和单摆周期.同时考虑到实验中需要改变摆线的长度、光电门的位置，本文设计了摆长调节装置和配套的可移动光电门，用于追踪摆球的移动. 实验装置如图1所示. 摆线通过固定旋钮后与游标卡尺的游标连接在一起.

图1 改进后的单摆实验装置图

实验中发现采用不同材质、直径的摆线对实验结果有较大影响，主要是由于摆线的质量不可忽略，并且摆线并非完全无弹性，导致实验过程中摆线的改变量并不完全等于两次游标卡尺的读数之差. 因此本文对不同材质、不同直径的摆线进行了多次重复测量. 采用的摆线共有5种，如表1所示.

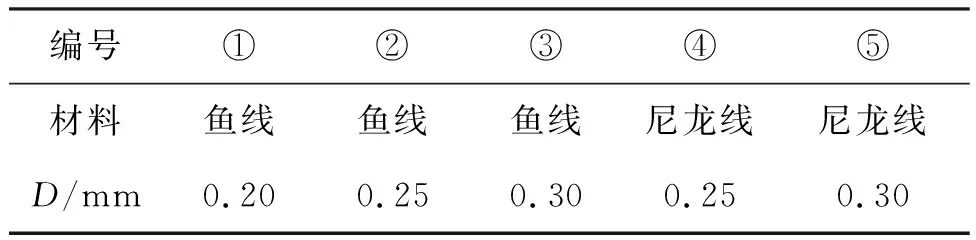
表1 摆线的材料和直径D

1.2 长度测量

直接测量摆长时由于采用毫米刻度尺，且摆长的起止位置难以精确确定，其测量精度较低. 因此本实验的测量方案改为用游标卡尺精确测量每次摆长的改变量.

实验中摆线长度的变化范围在32 cm～62 cm.确定摆长范围后，受摆球直径和光电门尺寸的限制，每次实验中，使振幅约为2.7 cm，这样可以保证摆动的最大角度小于5°.

由于摆长固定时，连接处细线的静摩擦力向上. 在改变摆长时，应使连接处的滑动摩擦力也向上，和静摩擦力保持同一方向，故采取逐步增大摆长的方式测量.

1.3 时间测量

实验中用光电门测单摆摆动的时长和周期数，采用的数字计时器是4位数显.实验中发现，在不同摆长下测单摆摆动10个周期的时长时，摆长较短测得的时间不足10 s，因而光电门的测量数据可以精确到0.001 s；而摆长较长时测得的时间超过10 s，光电门的测量数据只能精确到0.01 s. 为了保证实验的较高精度，应使得在摆长较短或较长时光电门的测量数据都可以精确到0.001 s(时长小于10 s)，故单摆周期的选择受到了一定限制. 进一步考虑到为了减小实验数据的偶然性，实验应当多次重复测量，单摆周期数选在4～8个周期内可以满足上述要求. 通过控制变量，对于每一个摆长分别取测量4、6、8个周期的时长，记为4T、6T和8T.摆动周期的平均值(nT)/n(n=4, 6, 8)如表2所示，其中L为游标卡尺的读数. 综合三组数据，发现周期测量的偏差都小于0.1%，在后续的实验中都统一测量6个周期的时长.

表2 在同一摆长处取不同周期数时的平均摆动周期

2 计算方法

从单摆测重力加速度的实验原理出发，摆球的运动方程为

(1)

得到单摆周期为[3-5]

(2)

(3)

在本实验中，通过多次改变摆长测量重力加速度g. 设单摆初始摆长为L0，摆长改变量为ΔL

(4)

(5)

推出

(6)

多次改变ΔL的大小，测出对应的T. 如对ΔL(或L0+ΔL)和T2做直线拟合可得到斜率k，则可得重力加速度g为

g=4π2k

(7)

3 结果与讨论

3.1 两种改变摆长方式的对比分析

用同一种鱼线分别采取摆长逐渐增大和逐渐减小的方式，对重力加速度进行测量，每个摆长下重复测量周期5次，测量得到的实验数据(游标卡尺读数L及6个摆动周期的时长6T)分别记录在表3和表4中. 通过对数据拟合处理，可以得到重力加速度g.

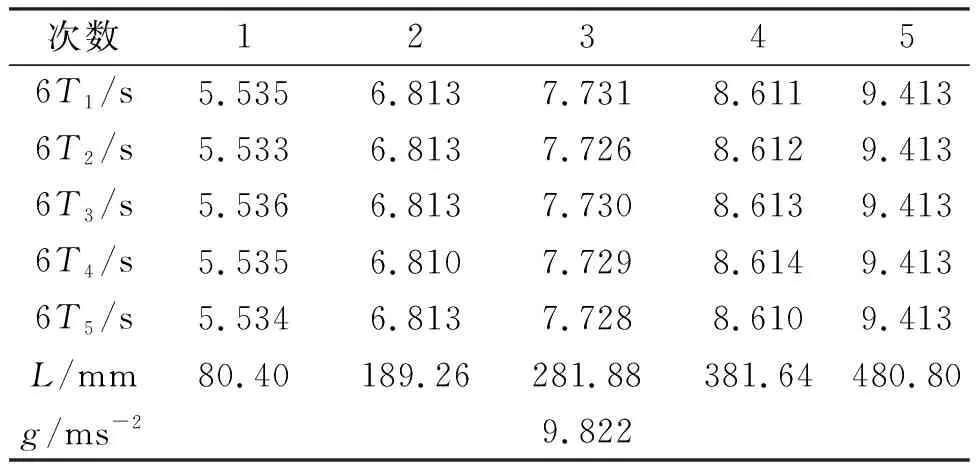
表3 摆长逐渐增大的实验数据

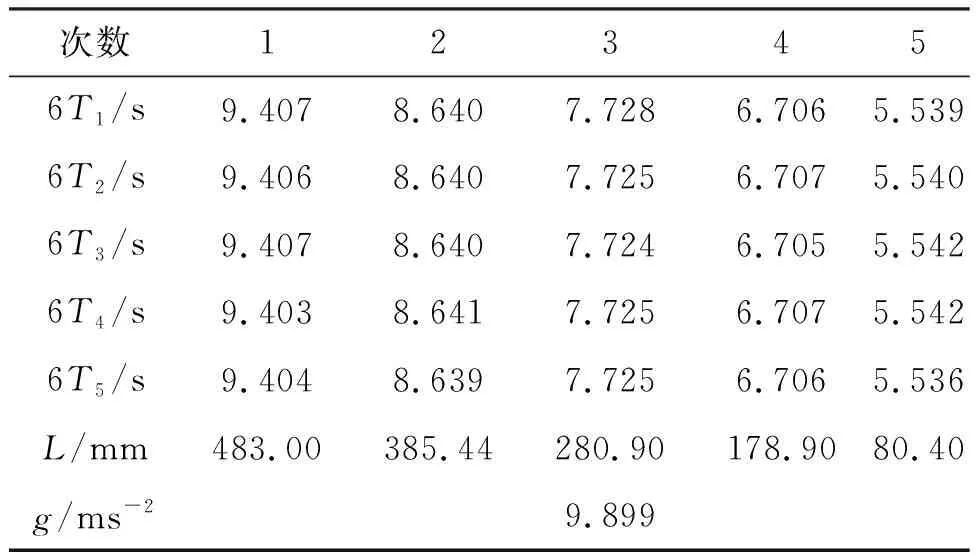
表4 摆长逐渐减小的实验数据

从鱼线测量的数据可以看出，摆长逐渐增大比摆长逐渐减小时测得的重力加速度值更加接近公认值，误差更小. 此实验结果验证了先前在长度测量部分的设想，即在改变摆长时应使连接处的滑动摩擦力也向上，和摆长不变时的静摩擦力保持同一方向. 因而采取摆长逐渐增大的方式测量.

3.2 不同直径、不同材质的摆线的比较

实验中选取了不同直径不同材质的线共5种，分别将其作为摆线，进行多次测量，每一种线测量5次，得到重力加速度g值，比较摆线的质量和弹性对实验结果的影响.

这5种线分别为：直径0.20 mm 鱼线、直径0.25 mm鱼线、直径0.30 mm鱼线、直径0.25 mm尼龙线、直径0.30 mm尼龙线.

以直径0.30 mm尼龙线的一组实验数据为例，表5是实验中测得的原始数据. 对ΔL和T2线性拟合，所得结果如图2所示，得到斜率k=249.8 mm/s2，置信概率为0.95时的误差uk=0.5 mm/s2，则重力加速度g=9.862 m/s2，测量误差ug=0.020 m/s2，相对误差ug/g=0.0020. 查得合肥地区的重力加速度为9.7947 m/s2，因此可算得测量结果与公认值之间的相对偏差ur为6.9×10-3. 表6列出了直径分别为0.25 mm、0.30 mm的尼龙线的实验测量结果、测量的相对误差以及测量值与公认值之间的相对偏差. 图3是直径分别为0.25 mm、0.30 mm的尼龙线的实验测量结果分布图.

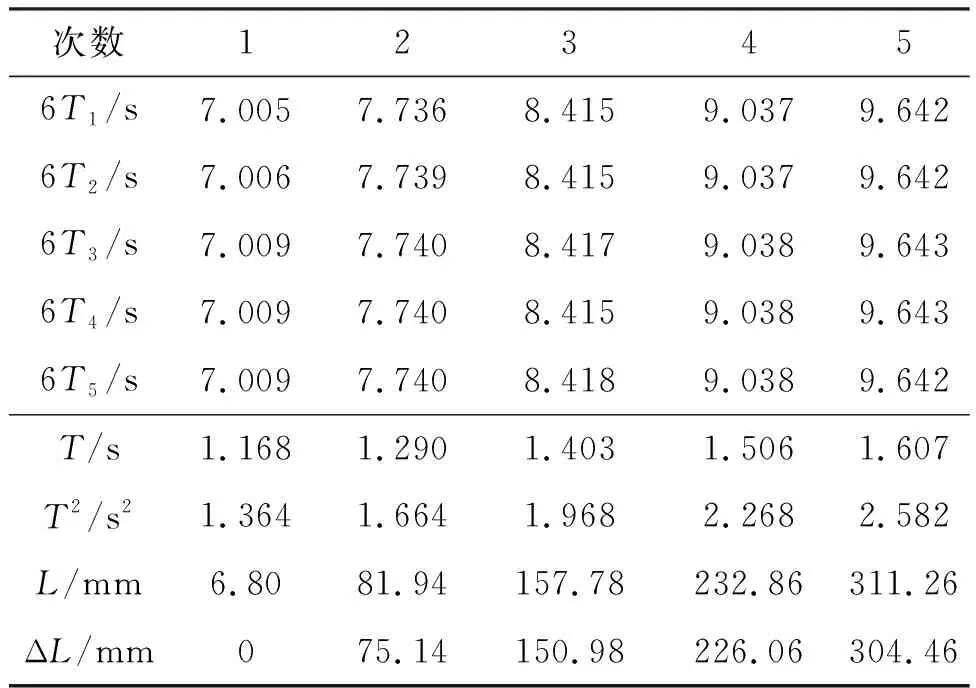
表5 直径0.30 mm尼龙线的实验数据

图2 直径0.30 mm尼龙线的实验数据拟合图

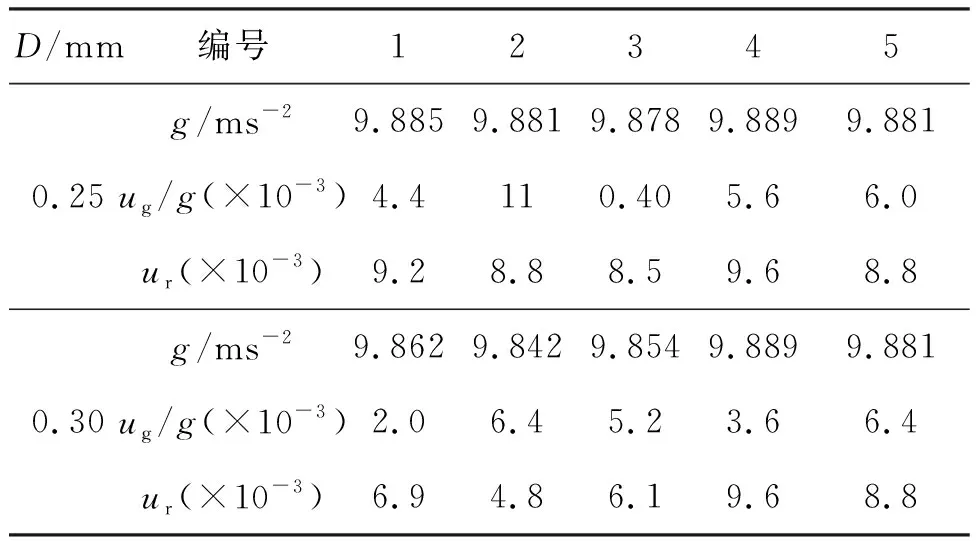
表6 不同直径(D)尼龙线的实验测量结果、测量的相对误差ug/g，以及测量值与公认值之间的相对偏差ur

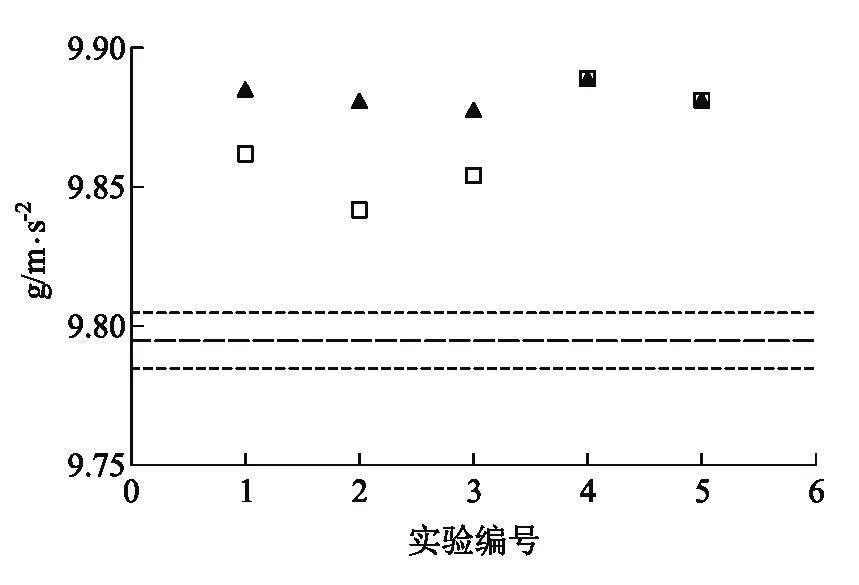
图3 直径分别为0.25 mm、0.30 mm的尼龙线的实验结果(图中实心三角形、空心正方形分别对应直径0.25 mm尼龙线、直径0.30 mm尼龙线的实验结果，长虚线是理论重力加速度值，两条短虚线是理论重力加速度值的千分之一误差的上下限)

表7列出了直径分别为0.20 mm、0.25 mm、0.30 mm的鱼线的实验测量结果、测量的相对误差以及测量值与公认值之间的相对偏差，图4为直径分别为0.20 mm、0.25 mm、0.30 mm的鱼线的实验测量结果分布图.

表7 不同直径(D)鱼线的实验测量结果、测量的相对误差ug/g以及测量值与公认值之间的相对偏差ur

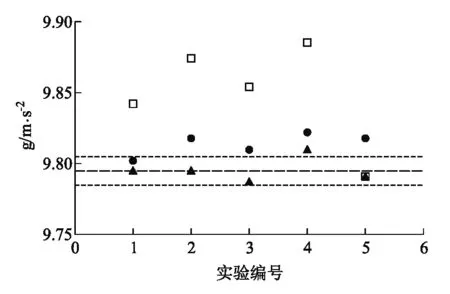
图4 直径分别为0.20 mm、0.25 mm、0.30 mm的鱼线的实验结果(图中空心正方形、实心圆圈、实心三角形分别对应直径0.25 mm鱼线、直径0.30 mm鱼线、直径0.20 mm鱼线的实验结果，三条虚线的物理含义同图3)

在两种不同直径的尼龙线中，直径0.30 mm的尼龙线测得的重力加速度g值更接近准确值. 在三种不同直径的鱼线中，直径0.20 mm的鱼线测得的重力加速度g值最接近准确值，直径0.30 mm的鱼线次之，直径0.25 mm的鱼线测得的重力加速度g值误差最大. 其中以直径0.20 mm的鱼线为摆线所测得的重力加速度g与公认值之间的偏差都在0.1%左右，其中80%测量值的偏差在0.1%以内，获得了较高的测量精度.

表8列出了直径同为0.25 mm的尼龙线和鱼线的实验测量结果、测量的相对误差以及测量值与公认值之间的相对偏差，图5为直径同为0.25 mm的尼龙线和鱼线的实验测量结果分布图.

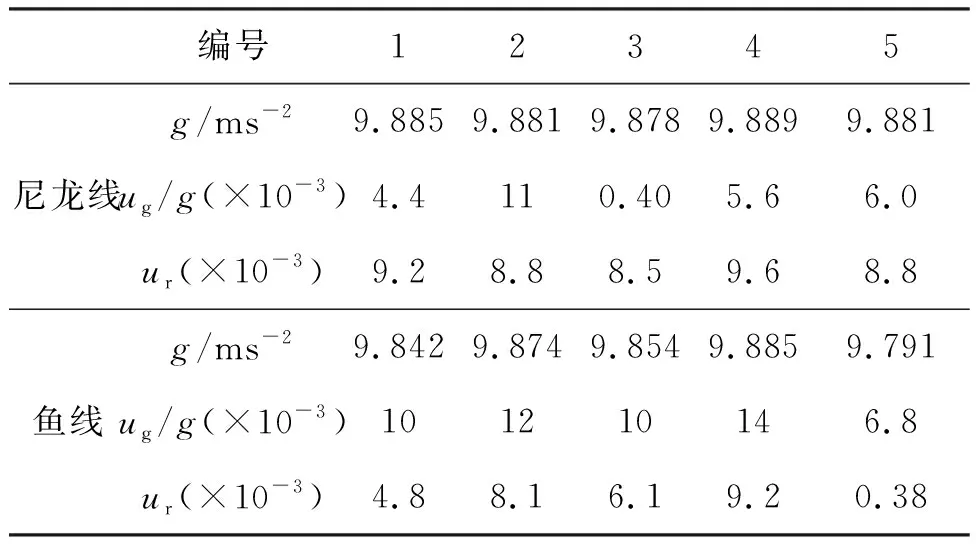
表8 直径为0.25 mm的尼龙线和鱼线的实验测量结果、测量的相对误差ug/g以及测量值与公认值之间的相对偏差ur

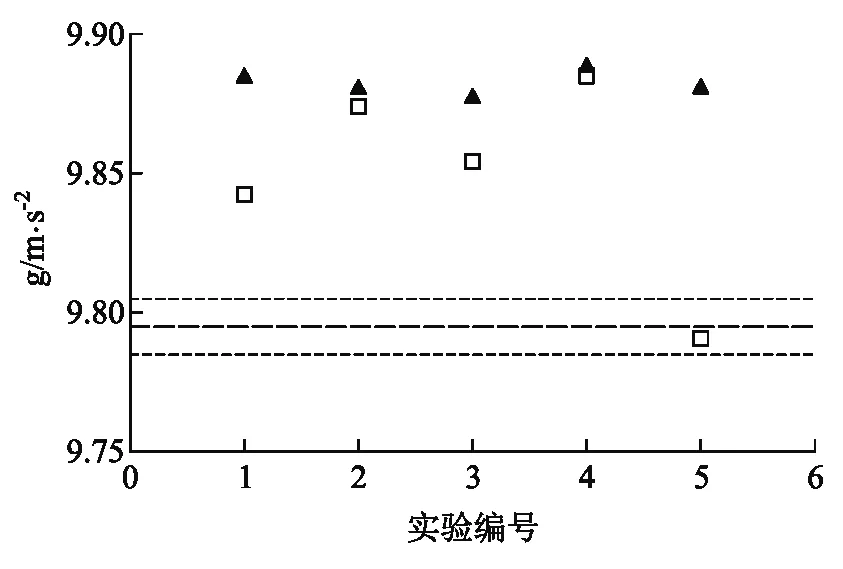
图5 直径为0.25 mm的尼龙线和鱼线的实验结果(图中实心三角形、空心正方形分别对应直径0.25 mm尼龙线、直径0.25 mm鱼线的实验结果，三条虚线的物理含义同图3)

表9列出了直径同为0.30 mm的尼龙线和鱼线的实验测量结果、测量的相对误差以及测量值与公认值之间的相对偏差，图6为直径同为0.30 mm的尼龙线和鱼线的实验测量结果分布图.

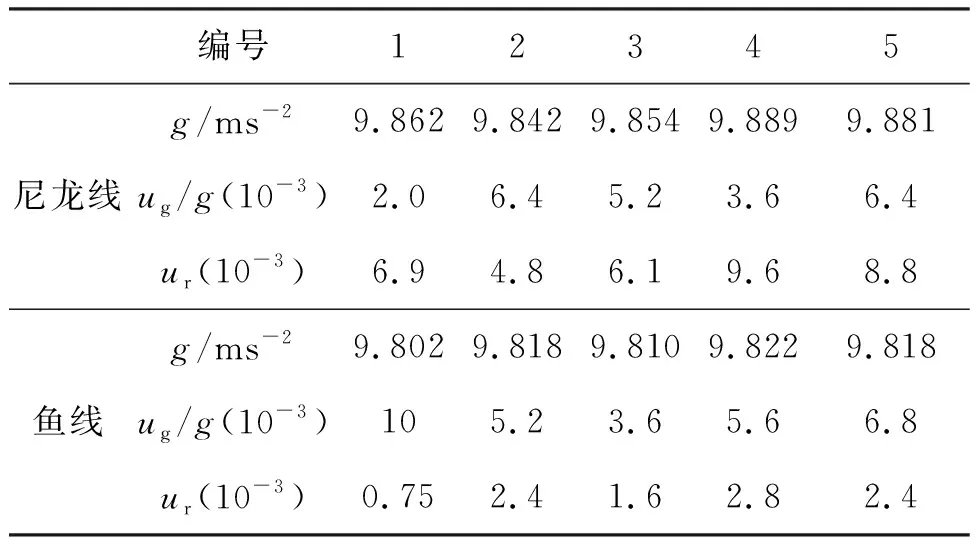
表9 直径为0.30 mm的尼龙线和鱼线的实验测量结果、测量的相对误差ug/g以及测量值与公认值之间的相对偏差ur

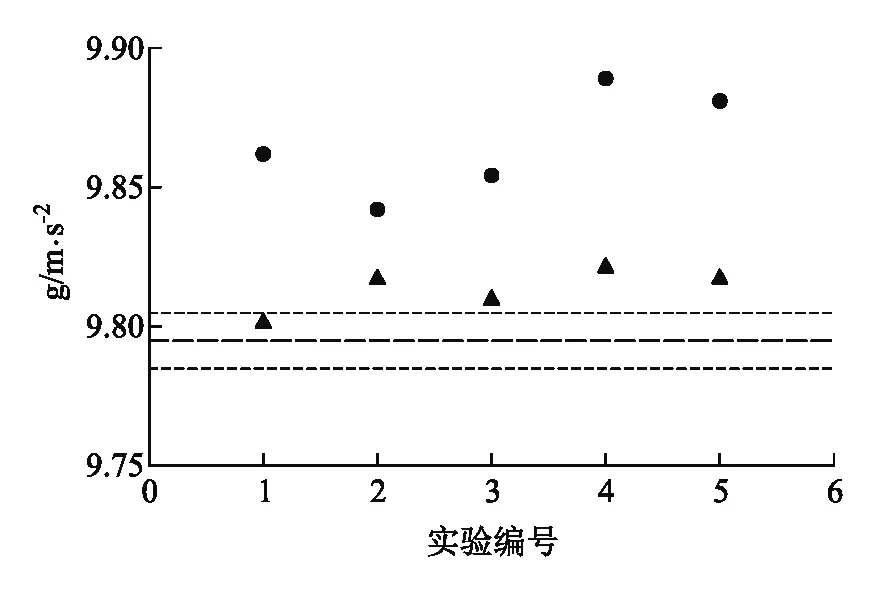
图6 直径为0.30 mm的尼龙线和鱼线的实验结果(图中实心圆圈、实心三角形分别对应直径0.30 mm尼龙线、直径0.30 mm鱼线的实验结果，三条虚线的物理含义同图3)

在两种不同材质的摆线中，无论直径为0.25 mm还是0.30 mm，采用鱼线测得的重力加速度g值均优于采用尼龙线测量的结果.

通过以上几组数据的分析可以发现：

1) 直径相同时，鱼线的测量结果明显优于尼龙线. 由于尼龙线是由三股细线绕制而成，实验时摆线的旋转不可避免，尼龙线越收越紧，摆线长度的实际变化量与测量值偏差较大，并且尼龙线质量相对较大，因此实验误差相对较大.

2) 不同直径的摆线对测量值的影响并不与直径呈线性相关. 摆线直径增大时，其质量增大，会增大实验误差，但根据杨氏模量E的定义公式E=FL/SL. 对于材料相同、直径不同的摆线，在摆线长度L和摆线受力F相同的情况下，摆线直径增大时，即横截面积S增大时，摆线因受力产生的形变量ΔL减小，因摆线伸长而带来的实验误差减小.因此对于材料相同、直径不同的摆线，不同直径导致以上两方面的差异都会对实验结果造成影响.

3.3 考虑单摆周期公式的一阶小量后对实验结果的影响

由单摆周期公式(2)，当θ很小时，近似得到公式(3). 在考虑单摆周期公式中的一阶小量之后，近似为

对直径0.25 mm的鱼线数据进行一阶小量的修正，结果如图7.

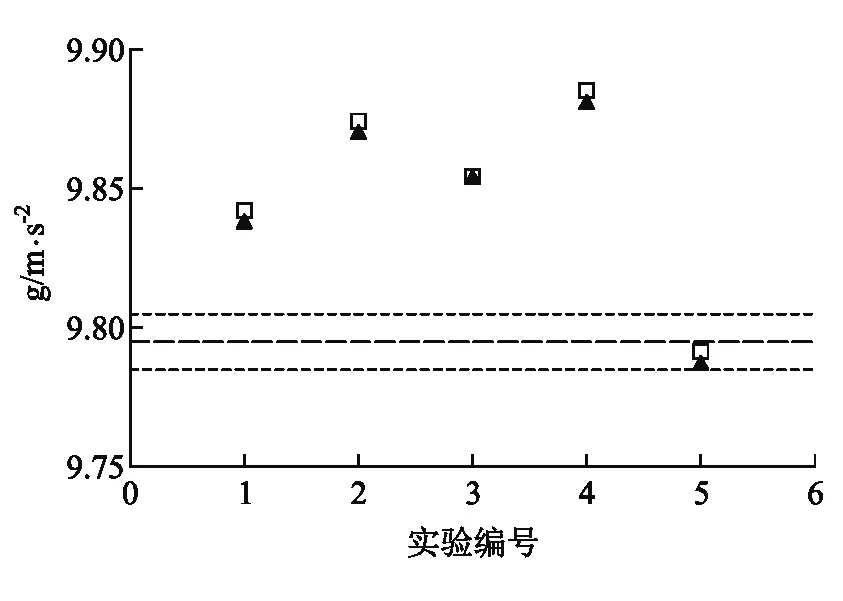
图7 直径0.25 mm鱼线，考虑单摆周期公式的一阶小量前后的实验结果(图中空心正方形、实心三角形分别对应直径0.25 mm鱼线考虑一阶小量修正前后的实验结果，三条虚线的物理含义同图3)

考虑单摆周期公式的一阶小量修正后的结果比未修正前(即忽略一阶及以上小量)的结果更接近真实值(实验编号5的数据可认为是实验的偶然性).但是否考虑单摆周期公式的一阶小量对实验结果的影响远小于摆线的直径和材质对实验结果的影响.

4 结论

通过将直接测量单摆摆长改进为测量摆长的改变量，可以提高重力加速度的测量精度，最佳实验条件下重力加速度的测量精度可达到0.1%. 在实验测量过程中，改变摆长时应使摆长逐渐增大.

在本文选取的5种不同的线中，直径0.20 mm的鱼线测量结果最优. 考虑单摆周期公式的一阶小量后使得实验结果更接近准确值. 但是否考虑单摆周期公式的一阶小量对实验结果的影响远小于摆线的直径和材质对实验结果的影响.