障碍物环境下电波传播的分区计算方法

李安琪 尹成友 甘泳机

（国防科技大学电子对抗学院，合肥 230037）

引 言

当今社会，在各个领域，不论是信息通信还是国防建设，研究不同地形环境下的电波传播问题变得越来越重要，因此考虑到实际地形情况，研究存在障碍物下的电波传播分析与计算非常必要.近年来，用于计算预测电波传播的方法主要有：模式理论法[1-3]、光学近似方法[4-5]、半经验公式法（ITU-R标准）[6]、时域有限差分法[7]、抛物线方程(parabolic equation, PE)近似法[8-10]. 其中PE是由波动方程近似化简之后得到的，属于一种迭代步进方法，是研究电波传播问题时最常用的方法，具有稳定性好和计算精度高的优点. 其他常用的方法，如模式理论法只适用于某些特定的情况，射线追踪法的精度不高，矩量法(method of moment, MoM)的计算量大，只适用于计算短距离传播的情况.

PE求解电波传播问题如图1所示. 在使用经典PE方法求解时将地面与障碍物视为整体，等效为起伏地形来处理，这种计算方法存在一定的缺陷：一是没有考虑障碍物与普通地形不同，两者介电常数存在差异；二是障碍物的存在导致电波传播的仰角过大，普通的PE近似不再成立[11]；三是没有考虑障碍物内部场值变化对空间中场值分布的影响. 因此实际上计算整个空间内场强的分布情况时，我们需要额外考虑存在障碍物的情况.

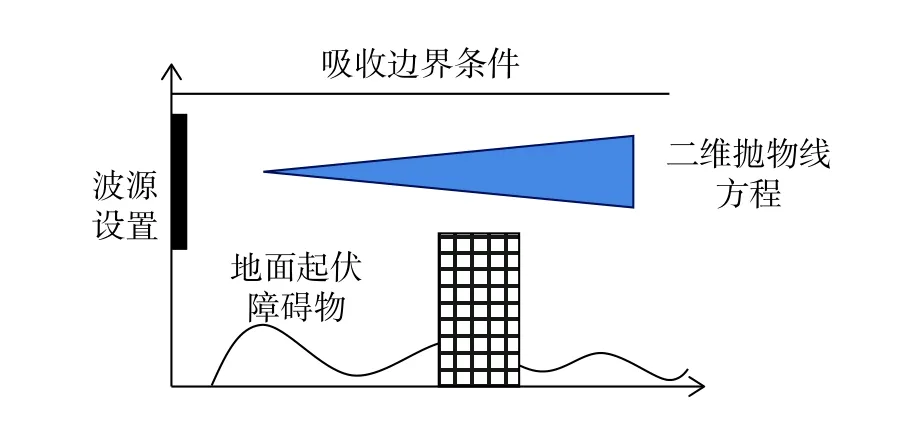
图1 PE法求解复杂环境电波传播示意图Fig. 1 Schematic diagram of wave propagation in complex environment

目前对于这个问题的主要处理方法来自于文献[12]，将障碍物上方空间计算的下边界往障碍物之下延伸一小段，内部空间的计算也往障碍物之上延伸至无穷远处，这样障碍物的上方和内部区域都变成了无穷大的区域，均可以使用离散混合傅里叶变换(discrete mixed Fourier transform, DMFT)进行求解，同时将连接处区域的场值使用两种算法的平均值代替. 显然这种方法存在一定的欠缺：向下延伸一小段的长度并没有给出计算方法，也没有较好的对这一小段长度进行求解的办法；该方法选取了边界上的一小段求平均值来保持场值连续，但这段的距离也没有较好的办法直接得出，因此计算精度不高；没有考虑到两个区域之间的互相影响，所以这种方法存在一定缺陷，我们需要寻求其他的方法来解决这个问题.

而当前已知的计算电波传播PE的求解方法主要有：有限差分(finite difference, FD)方法[13-14]、有限元方法[15-17]、分步傅里叶变换(split step Fourier transform, SSFT)方法[18-21]. 其中，FD法和有限元方法都属于数值计算方法. SSFT方法计算速度快，计算性能稳定，远距离电波传播问题上优势明显.有限元方法适用于低频信号，不适用于大气波导问题的求解，且计算量随着距离的增大而增大，也不适用于远距离问题的求解. 虽然FD方法和SSFT方法相比，计算时间和计算效率都不高，但可以更为灵活地处理边界条件.

本文将区域分解思想应用于该问题的求解，各子域分别采用不同算法进行计算，在目标区域采用差分法求解，并对边界进行处理，保证边界场值连续，在原先PE方法上提高了计算效率，扩展了适用范围.

1 问题描述

区域分解算法是指将整个区域上的大问题分解为若干子区域上的小问题分别进行求解，获得每个小问题的结果之后，通过级联即可获得整个区域上的解[22]. 这样每个区域上的问题不但可以独立求解，而且可以选择适合于该子域的最有效的方法，不同子域选择不同解法，并且求解规模较小. 假设地面为理想导体的情况下，对于电波传播来说，在遇到障碍物时，可以将分析的区域分解为无障碍物区和有障碍物区，具体如图2所示的 Ω1、Ω2区.

图2 区域分解示意图Fig. 2 Schematic diagram of domain decomposition

在 Ω1区电波传播满足PE，其上边界采用吸收边界，可以认为其到无穷远，下边界连接在障碍物顶部，可以采用阻抗边界条件，因此该区域PE的求解可以采用DMFT步进求解.

在Ω2区电波传播一样满足PE，其下边界是理想导体，对于水平极化波是第一类边界条件，而垂直极化属于第二类边界条件；其上边界与Ω1区的下边界相连，同样满足阻抗边界条件. 由于Ω2区上下封顶，PE不便于使用DMFT进行求解，因此该区域可以采用FD求解.

2 双向PE DMFT的计算

2.1 双向PE的推导

假设求解时谐场为 exp(jωt)，其中ω为角频率.在二维直角坐标系中我们对场量 Ψ 在不同极化情况下分别定义为方向. 则场量Ψ 满足二维波动方程

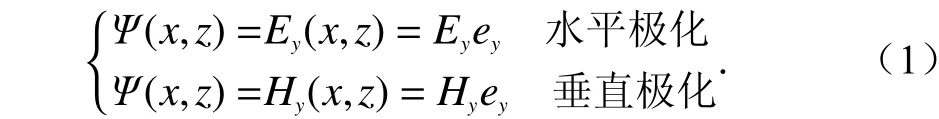
电磁波沿轴向传播，这里选择x轴为正向传播

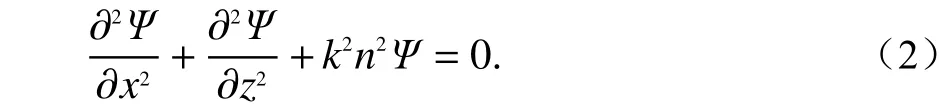
式中：k是媒质均匀环境中的波数，Ω1区中k为自由空间波数k0，Ω2区 中k为障碍物介质波数代表修正后的大气折射率. 在上述理论分析的基础上，假设折射率n不 随距离x变化而变化，将式(2)因式分解后得

分别引入两种不同的相位解调因子[3]

式中，ΨfΨb分别代表前向场和后向场. 因此本文采用的都是双向PE算法，将式(4)分别代入因式分解后所得式，求得前向传播和后向传播PE如下：

要得到方程(2)的解，方程(5)的前向和后向就必须在同一系统中进行求解，给定初始值和底部、顶部的边界值，就可以用步进法求解. 在求解完成后我们还会采用对前后场进行相位修正的办法来进一步改善计算精度，解决整体场值相位不匹配的问题[23].

2.2 边界条件的讨论

前面推导中都假设地面是理想导体情况下处理的，所以在平坦地面区域可以直接采用SSFT方法求解. 但在介质障碍物区域，对于 Ω1区的上边界，该假设不再成立，因此需要另外处理. 一种简便的方法是采用阻抗边界条件来获取边界上的场值关系. 媒质1和媒质2的分布如图3所示.

图3 阻抗边界示意图Fig. 3 Schematic diagram of impedance boundary

2.2.1 广义阻抗边界条件

对于水平极化波情况：Ψ=Ey，由Maxwell旋度方程可得

因此有边界条件为

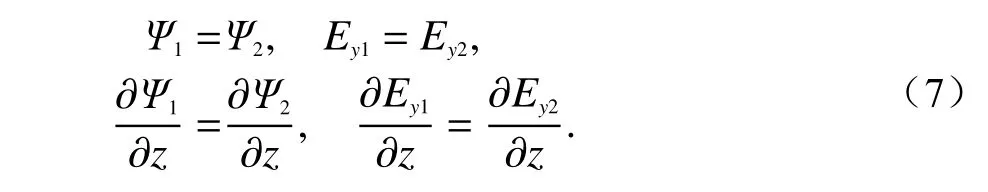
假设媒质2是均匀的，其复相对介电常数为

同样对媒质2采用PE求解，假设在分界面下初始场为0，近似认为在分段内不是x的函数，对式(4)中前向传播方程中的x分量进行Laplace变换，则

式中：k是自由空间波数；U(s,z) 为u(x,z)关于x的Laplace变换结果.

因为媒质2是均匀、有耗的，因此其电磁波在z→−∞是有界的，甚至是指数衰减的，有

α(s)应该具有负虚部，将式(10)代入(9)，并利用谱域的思想，得到

这样媒质2在边界处满足

利用媒质1与媒质2的边界切向场的连续性，可以得到媒质1边界满足

根据上面的分析，对于水平极化情况，比较式(12)和(13)可得到

同理可得垂直极化情况. 上述推导的关系式称为广义阻抗边界条件.

2.2.2 Leontovich阻抗边界条件

上述阻抗边界条件是在谱域下得到的，假设一个平面波入射到表面上：

对其进行Laplace变换得到

当对应的电磁波为消逝波，我们可以忽略. 当掠入射角较小时，对应窄角PE情况，对于水平极化波，有

同理可得垂直极化波情况. 显然这种边界条件适合 Ω1区的下边界.

2.2.3 Ω2区域上边界条件的确定

对于Ω2区的上边界来说，其边界由图3可以看出，此时它与 Ω1区 相比，两种媒质正好颠倒相当于空气，不具有大的模值时，上述Leontovich阻抗边界条件不再适用. 但由前面分析知，在介质的分界面上，对于水平极化波有如式（7）所示的情况. 同理可得垂直极化波情况.

同时由上述分析可得，Ω1区的下边界满足Leontovich 阻抗边界条件. 由于式（17）中δ(s)与s无关，对式（13）进行Laplace反变换可以得到水平极化波情况下 Ω1区的下边界条件，同理可得垂直极化波情况下的Ω1区下边界条件，因此可以表示为

假设Ω1区 贴近边界处折射率由边界切向场的连续性和式(18)可得 Ω2区的上边界条件为

由于上下区域在边界处交汇，边界处的值在步进过程中会同时代入两种算法进行迭代计算，我们选择将两种算法计算出的边界值取平均之后，再作为初值代入下一次的迭代过程. 这样既确保了边界切向场连续，又考虑了上下区域电波传播过程中场值之间发生的耦合作用，避免突然截断所导致的计算误差.

2.3 双向PE的DMFT方法求解

式(4)中对Q因子的处理方法有很多种，这里主要从宽角近似出发，将Q按Feit-Fleck模型展开，对应的Q展开式为[24-25]

将Q代入到式(4)中的Feit-Fleck宽角近似下的双向波动方程，通过DMFT方法求得步进公式uf(x+∆x,z),ub(x−∆x,z)：

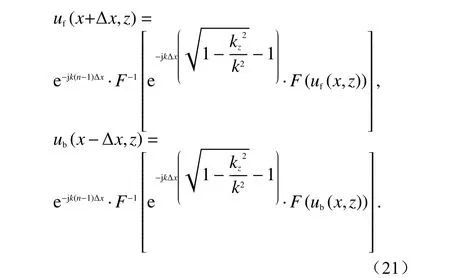
3 PE的FD计算方法

3.1 宽角PE的差分近似

使用FD法来求解PE，实际就是将PE中的一阶偏微分和二阶偏微分都用差分形式改写，从而通过步进方法求解，获得整个计算区域内的场值. 记：

式 中，zp为 垂 直 网 格 点. 令x0、x1、···、xm、···、xN表示水平网格点，x方向即为步进方向，网格划分如图4所示. 为了进行中心差商处理，设的中点为则可以得到点处的对x一阶差分和对z的二阶差分:

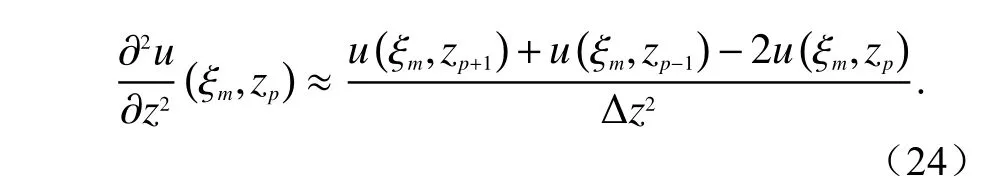
在PE的求解中，首先需要得到关于u的标量方程. 标准PE的限制主要在于难以准确计算大传播仰角的波束，由此可见标准PE是一个窄角处理方法. 因此，为实现宽角情况下的电波传播计算的PE方法，采用pade近似得到Q的近似表达式，即

取a=0.75,b=0.25，称之为Claerbout逼近. 下面开始对场强进行求解.

图4 FD网格划分示意图Fig. 4 Schematic diagram of finite difference mesh generation

3.2 电磁波前向传播的情况

首先讨论前向差分时前向传播方程，利用Claerbout展开：

将式（26）代入（4）中的正向传播方程后进一步化简得到计算方程

整理化简可得

式(28)为第p=1,···,N−1个方程. 为了完整起见，还需要包括上下边界的差分方程.

3.2.1 理想导体地面下边界的处理

对于水平极化，由于其值恒为0，相对简单，其边界方程为

对于垂直极化，则需要导出宽角PE的边界条件.

3.2.2 介质内部上边界的处理

此时仍采用宽角差分方程，由式(27)和(4)，取z=N,x=(xm−1+xm)/2点进行差分处理，依照式（19）有

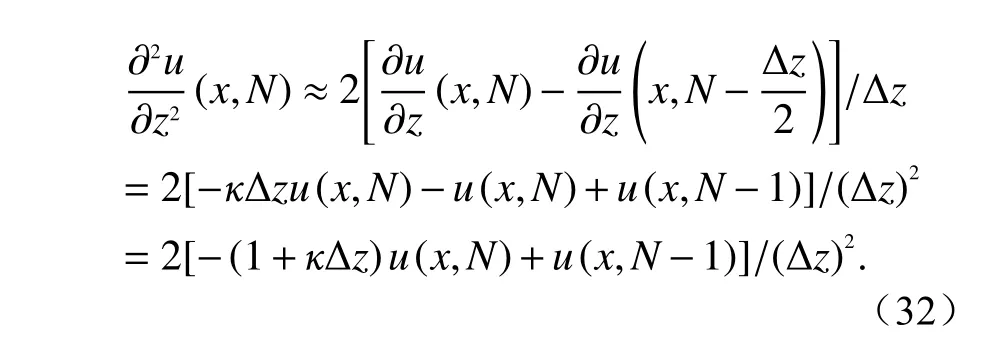
将式（23）和（32）代入式（27）得到计算方程

这样式(28)、(31) 和(33)共同构成了水平极化时0～N的前向差分PE.

PE差分解递推结构用矩阵可表达为

式中：Um是在xm处的场向量，

对于水平极化波，Am是一个三对角矩阵，

这种Crank-Nicolson FD结构，由于具有三对角特征，方程计算方便，而且具有非常好的数值特性，可以采用追赶算法快速计算，则方程(34)可以改写为

根据式(36)和(37)求解该矩阵，得到前向传播的Um.

3.3 电磁波后向传播的情况

后向传播的迭代情况同前向传播一致，所以后向传播的迭代矩阵和前向的完全一致.

通过前面的推导我们得到了电波传播矩阵，要求解差分方程，传统的方法是对Am求逆，但计算量大且速度慢，目前比较方便的方法是 LU算法，就是将正定的三对角系数矩阵A分解为上三角矩阵U和下三角矩阵L. 本文在 LU算法的基础上采用追赶算法，这种算法非常简单，且具有数值稳定的特点，在求解三对角矩阵方程中应用也很广泛[26].

将其具体应用到FD矩阵方程中，实现步骤如下：

1)计算Vm=BmUm−1；

2)对Am进行Crout分解，参数均已知；

3)求解方程组Ly=Vm；

4)求解方程组Ux=y，最终得到x.

通过以上4个步骤可由第m−1步的场值导出第m步的场值，因此只要给定每一步的初始场即可得到任意位置的场值.

4 仿真结果

4.1 单矩形介质障碍物情况下的电波传播分析

图5为单矩形障碍物仿真示意图，假设地面为理想导体，发射源工作频率30 MHz、高80 m、波束宽度 20◦、水平极化，辐射源等效辐射功率（equivalent radiation power, EIRP）为W，Z0为自由空间波阻抗. 矩形模型位于距离发射源752 m处，介质障碍物模型宽16 m、高100 m，媒质的电导率为10−5、相对介电常数为4. 计算得到的整体场强分布如图6所示. 从图6可以看到，地面反射与直达波之间形成干涉，导致波瓣分裂现象. 此外，介质障碍物产生的反射波与直达波形成干涉，导致各波瓣上形成干涉条纹. 障碍物内部也有相应的干涉存在.

图5 单矩形障碍物仿真示意图Fig. 5 Simulation diagram of a single rectangular medium obstacle

图6 单矩形介质障碍物情况下的Ey分布图Fig. 6 Distribution diagram of Ey in the case of a single rectangular medium obstacle

图7为三种算法在相同给定观察高度80 m下的整体场值比较，其中 PE算法是文献[12]计算结果，新PE算法是本文所提新算法结果. 可以看出，PE算法和新PE算法结果都与MoM的吻合较好，但新PE算法似乎吻合更好.

图7 单矩形介质障碍物情况下80 m处的Ey比较图Fig. 7 Comparison of Ey at 80 m in the case of a single rectangular medium obstacle

为进一步观察这两种方法在不同区域的场值计算精度，对图7提取局部场值如图8所示. 由图8（a）障碍物之前的局部场值可以看出，在等效源模型的基础上，障碍物之前新PE算法相位修正后的计算结果与MoM计算结果几乎一致，验证了新PE算法计算结果的精确性. 图8（b）中，新PE算法与MoM在障碍物内部区域计算的场值略有差异，而和文献[12]中的PE算法近乎一致. 这种误差来源于PE算法本身的缺陷，因为辐射源具有一定的波束宽度，波源照射到障碍物表面时不是垂直入射，而且角度偏差越大，障碍物内的计算误差越大. 图8（c）中，靠近障碍物部分时新PE算法与MoM的场值略有差异，但越是远离障碍物时，二者的结果就越一致. 在计算过程中，MoM平均用时159.6 s，文献[12]中的PE算法用时16.9 s，而新PE算法则用时7.6 s，计算速度优势明显.

图8 单矩形介质障碍物情况下Ey的局部场值比较Fig. 8 Comparison of local field values of Ey in the case of a single rectangular medium obstacle

4.2 双矩形介质障碍物情况下的电波传播分析

图9为双矩形障碍物仿真示意图，假设地面为理想导体，发射源工作频率30 MHz、高80 m、波束宽度 20◦、 水平极化，辐射源EIRP为W，Z0为自由空间波阻抗. 双矩形模型位于距离发射源750 m和900 m处，介质障碍物模型宽22 m、高100 m，媒质的电导率为1 0−5、相对介电常数为3. 双矩形介质障碍物下的整体场值分布如图10所示. 可以看出，直达波、地面反射波以及介质障碍物的反射波形成的波束与图6类似.

图9 双矩形障碍物仿真示意图Fig. 9 Simulation diagram of double rectangular medium obstacles

图10 双矩形介质障碍物下的Ey分布图Fig. 10 Distribution diagram of Ey in the case of double rectangular medium obstacles

图11所示为接收高度为80 m处双矩形介质障碍物下新PE算法和MoM两种算法得到的整体场值比较. 可以看出，在双矩形介质模型下，两种算法所得整体场值依然吻合得较好.

图11 双矩形介质障碍物情况下80 m处的Ey比较图Fig. 11 Comparison of Ey at 80 m in the case of double rectangular obstacles

图12所示为双矩形介质障碍物下新PE算法和MoM两种算法得到的局部场值比较. 可以看出，和单矩形模型类似，在障碍物之前新PE算法相位修正后的计算结果与MoM计算结果几乎一致，障碍物内部区域计算的场值略有差异，障碍物后的靠近障碍物部分两种算法的场值略有差异，随着离障碍物距离越远，二者的结果越一致.

图12 双矩形介质障碍物情况下Ey的局部场值比较Fig. 12 Comparison of local field values of Ey in the case of double rectangular medium obstacles

5 结 论

本文根据区域分解原理，提出了一种针对障碍物环境下新的双向PE算法. 该算法在无障碍物区域采用普通的DMFT算法，在障碍物区域进行区域分解，在障碍物上方的无限大区域采用DMFT算法，在障碍物内部的封闭区域则采用FD算法，有效解决了障碍物中电波传播问题. 在相同波源、天线等参数设置的基础上，用较为精确的MoM验证了近距离下新双向PE算法在存在单矩形和双矩形障碍物情况下的电波传播计算的精确性和有效性. 该算法与文献[12]已有的双向PE算法相比，新算法理论分析更为清晰，计算速度和精度都有一定提高. 本文研究的是规则形状障碍物地形下的电波传播问题，实际障碍物不一定是规则的形状，计算更加复杂，因此对不规则障碍物地形下的电波传播问题还需要作进一步研究.