一种基于分步线性最优估计的全球中低纬区域电离层foF2重构方法
陈龙江 甄卫民 欧明 於晓 宋方雷
(1. 中国电波传播研究所,青岛 266107;2. 电波环境特性及模化技术重点实验室,青岛 266107;3. 武汉大学电子信息学院,武汉 430079)
引言
电离层作为日地空间环境的重要组成部分,会对穿越其中的无线电波产生折射、反射、散射和吸收等效应,从而影响卫星导航、通信、雷达等诸多无线电信息系统的性能. 研究电离层的特征参数,掌握其时空变化特征和规律,对提升无线电信息系统的性能具有重要的实用价值[1]. 在诸多电离层特征参数中,电离层F2层临界频率foF2是短波通信、探测和电子对抗等领域最为重要的应用参数之一. 受太阳活动、地理位置、地磁扰动以及背景大气风场等多种因素的制约,电离层foF2呈现较为复杂的时空变化特征. 长期以来,电离层重构都是电离层研究的重点方向之一. 为了进一步提高电离层环境监测的精度和准确度,国内外学者对电离层foF2重构方法做了大量的研究. Stanislawska等人改进了Kriging方法,引入“电离层距离”来实现欧洲区域的电离层foF2重构[2-3]. 柳文等人在利用人工神经网络技术研究电离层月中值隔月变化规律的基础上,利用周年和黑子周期变化的数据训练网络,实现了电离层foF2等预测[4]. 王世凯等人在中国区域电离层重构中引入国际参考电离层(international reference ionosphere,IRI)[5]作为背景电离层约束,并对重构精度进行定量分析[6]. 刘瑞源等人以中国参考电离层(reference ionosphere of China,CRI)作为背景电离层,利用改进的克里格插值方法对中国区域电离层foF2进行重构,提高了重构的精确度[7]. 陈春等人在中国区域电离层foF2重构中同时考虑到纬度效应和经度效应,提高了区域重构的准确性和稳定性[8]. Galkin等以IRI作为背景场,利用实时同化映射技术进行空间插值,对全球电离层foF2重构[9]. 於晓基于弹性线性优化技术,利用中国电波传播研究所16个垂测站的foF2观测数据实现了中国区域电离层foF2重构[10]. Pignalberi等利用欧洲区域数字垂测仪自动判读的foF2和M(3000)F2数据,基于电离层IG12和R12最优化估计与克里格插值技术,建立国际参考电离层更新(international reference ionosphere update, IRIUP)模型实现欧洲区域电离层重构,有效提升了该区域电离层foF2及hmF2的重构精度[11].
针对全球范围内电离层测高仪分布较为稀疏的特点,提出了一种全球中低纬区域电离层foF2重构方法,该方法基于分步线性最优估计对电离层CCIR/URSI系数(由国际无线电咨询委员会/国际无线电科学协会联合提出的)进行调整,可大大降低电离层foF2重构时待估的未知系数数量,避免处理大型矩阵,从而可实现全球中低纬区域电离层foF2的快速准确重构. 基于2010—2016年的全球电离层无线电观测站(Global Ionospheric Radio Observatory,GIRO)测高仪[12]实测数据统计对比结果,验证了本文方法的有效性和准确性.
1 基于CCIR/URSI系数的foF2映射技术
IRI是研究电离层环境状态的基础模型之一,它利用CCIR/URSI系数映射技术计算电离层特征参数foF2的全球分布[13]. 该映射技术通过傅里叶级数展开来表示foF2的周日变化,即

式中:λG是地理纬度,−90◦≤λG≤90◦;φG是地理经度,−180◦≤φG≤180◦;T是世界时(U TC),以角度表示,−180◦≤T≤180◦. 傅里叶系数ai(λG,φG)是地理坐标和地磁坐标的函数,用以下级数形式表示:

式中:H(j) 是一组随着j变化的整数,H(j)=[11,11,8,4,1,0,0,0,0](j=0,1,2,3,4,5,6,7,8);χ是修正磁倾角纬度[14],χ=arctan(I(λM,φM)/cosφG),其中I(λM,φM)表示在地磁坐标 (λM,φM)上方350 km处的真实磁倾角;Ui,j,k是IRI中采用的CCIR/USRI系数,每组系数的个数为988.
将式(2)代入式(1),整理可得

式中:

从上文可以看出,IRI模型基于系数Ui,j,k可生成电离层特征参数foF2的全球分布,且在给定时间,IRI模型计算出的全球各点foF2的大小仅与系数Ui,j,k有关.
2 基于分步线性最优估计的电离层foF2重构方法
电离层重构是以多点观测数据,推断该参数在大面积区域连续的实时分布. 本文的基本思路是利用中低纬区域多个测高仪站点过去24 h的电离层观测数据分步调整系数Ui,j,k,进而实现中低纬区域电离层foF2重构. 具体实现步骤如下:
第1步 系数Ui,j,k扩 展. 将系数Ui,j,k的下标k的范围扩展到H(j)的最大值11,并且对扩展处的系数补零. 此时,式(3)可以改写为式(8)、(9)的形式,式(8)对应的是foF2的地理位置变化,式(9)对应foF2的地磁变化.

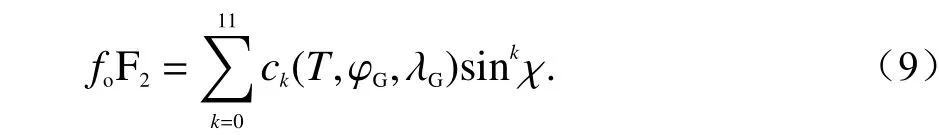
式中:

第2步 系数Ui,j,k初 始化. 引入校正因子Fa=R12/100以 获 得 等 效 黑 子 数R12[15],代 入Ui,j,k=完成系数初始化. 其中和分别代表太阳黑子数为0和100时的CCIR/USRI系数.
第3步 系数Ui,j,k三种变化调整. 先后引入校正因子和三组因子分别调整foF2周日变化、地理位置变化、地磁变化,如式(12)~(14)所示. 通过线性最小二乘拟合使得调整后的foF2与电离层观测数据之间误差的平方和为最小,进而求取校正因子. 最后,利用校正因子和分步调整式(2)、(10)和(11)对应的系数Ui,j,k.

CCIR/URSI系数Ui,j,k经过上述调整,其生成的中低纬区域foF2分布将与电离层观测数据的时间和空间相关性最佳匹配,可对电离层的实时状态进行重构. 相比单步线性最优估计方法,基于分步线性最优估计方法仅需要求解54个校正因子即可实现电离层foF2重构,而无需求解988个CCIR/URSI系数Ui,j,k,在目前全球电离层测高仪观测数据较为稀疏且存在缺失的情况下,可大大提升foF2重构过程中的稳定性和可靠性,从而满足全球中低纬区域电离层foF2快速、准确重构的目的.
3 结果与讨论
采用GIRO发布的中低纬度区域42个测高仪站点的foF2观测数据进行分析研究,该数据的时间采样间隔为15 min. 测高仪站点分布如图1所示,选择其中36个站点的数据参与中低纬区域电离层重构,其余6个站点的数据用于重构方法的有效性验证和误差分析.

图1 中低纬区域GIRO测高仪站点分布Fig. 1 Distribution of GIRO ionosonde stations in the middle and low latitudes
图2为2014年4月16日0 UT时刻,中低纬区域foF2重构结果与对应IRI结果,可以看出,与IRI相比,重构生成的foF2地图出现了明显变化,且重构的foF2值在多数区域出现下降. 从对比结果可以看出,通过CCIR/URSI系数调整,重构的电离层foF2与IRI模型默认的输出结果存在明显的差异.

图2 2014年4月16日00:00UT时刻中低纬区域foF2重构结果和IRI结果Fig. 2foF2 reconstruction result and IRI result in mid-low latitudes at 00:00UT on April 16, 2014
图3给出了参与方法有效性验证的6个测高仪站点2014年第98日—第106日共计8天的观测数据、foF2重构结果和IRI结果的比较. 从图3可以看出,重构结果与观测数据更为接近,且重构结果的变化趋势基本上与观测数据一致,吻合度明显优于IRI模型的计算结果. 同时,从图3可以看出,中纬4个站点(Juliusruh、Fairford、Millstone Hill、Eglin AFB)的重构结果与观测数据之间的吻合度要优于低纬的2个站点(Sanya、Anyang),这可能是因为低纬区域电离层比中纬区域的控制因素更为复杂. 进一步地,统计了2014年6个站点foF2重构结果、IRI结果与观测数据之间的绝对误差、均方根误差和相对误差,统计结果如表1所示. 可以看出,中纬4个站点foF2重构的绝对误差、均方根误差和相对误差均低于低纬2个站点,其中低纬的Sanya站的重构绝对误差最大,中纬的Juliusruh站的重构绝对误差最小,但两站重构的绝对误差均小于1 MHz. 另外,与IRI相比,2014年6个站点重构绝对误差和均方根误差的平均值分别减小了0.29 MHz和0.32 MHz,而相对误差的平均值下降了约5%,对比验证了本文提出重构方法的有效性.


图3 2014年6个站点的foF2观测数据、重构结果和IRI结果的比较Fig. 3 Comparison of observation data, reconstruction results and IRI results at 6 stations in 2014

表1 2014年6个站点重构和IRI的绝对误差、均方根误差和相对误差Tab. 1 Absolute error, root mean square error and relativeerror of reconstruction and IRI of 6 stations in 2014
由于电离层存在明显的年度变化,对所有参与方法有效性验证的测高仪站点各年整体的foF2重构误差和对应IRI误差进一步统计,图4给出了2010—2016年7个不同太阳活动年份下,foF2重构和IRI的绝对误差和均方根误差分布比较. 可以看出,foF2重构的绝对误差为0.45~0.72 MHz,均方根误差为0.65~1.1 MHz. 重构绝对误差和均方根误差都小于同年对应的IRI误差,计算7年的平均误差发现,重构的绝对误差和均方根误差相较于IRI分别下降了约38%和34%,再次验证了该重构方法的有效性. 从图4中还可以看出,重构误差从2010—2014年逐年增大,在2014年达到最大值后开始减小. 为说明太阳活动强度对重构精度的影响,我们统计了2010—2016年的年平均太阳黑子数,结果如图5所示. 分析发现,foF2重构绝对误差和均方根误差有随太阳活动强度增强而增大的趋势,与太阳活动存在较为明显的正相关性.接着,继续统计了2010—2016年7年重构相对误差,发现重构的相对误差无明显的年变化,各年重构的相对误差均在10%上下波动,这说明本文重构方法稳定性较好.


图4 重构和IRI的绝对误差和均方根误差的年度变化Fig. 4 Yearly variation of IRI absolute error and root mean square error of reconstruction

图5 2010—2016年的年平均太阳黑子数Fig. 5 Annual average number of sunspots from 2010 to 2016
同样地,根据电离层存在明显季节性变化的特点,图6给出了所有参与方法有效性验证的测高仪站点整体重构的绝对误差和均方根误差随季节变化的统计结果. 从图6可以看出,夏季重构误差最小,而其他三个季节则相差不大. 对于电离层而言,一般夏季期间电离层foF2处于全年的最小值,这可能是导致夏季重构误差相比较其他季节要偏低的原因.
由于电离层存在明显的当日变化的特点,图7给出了所有参与方法有效性验证的测高仪站点整体foF2重构均方根误差随地方时(LT)的变化结果.可以看出,白天重构的均方根误差小于夜间,重构的均方根误差除了在17:00之后出现明显增加外,其他时间段波动较小. 整体来看,重构方法有较好的稳定性.
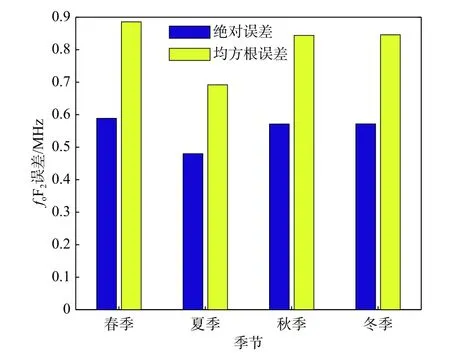
图6 重构绝对误差和均方根误差的季节变化Fig. 6 Seasonal variation of absolute error and root mean square error of reconstruction

图7 重构均方根误差随地方时的变化Fig. 7 variation of root mean square error of reconstruction with local time
4 结 论
电离层foF2是表征电离层状态变化的关键特征参量之一. 针对全球范围内电离层测高仪分布较为稀疏的特点,提出了一种基于分步线性最优估计的全球中低纬区域电离层foF2重构方法,并利用测高仪站点的电离层实测数据对重构方法进行了有效性验证. 基于2010—2016年的数据分析表明:
1) 相比于IRI模型,本文方法重构的电离层foF2与观测数据之间绝对误差和均方根误差分别降低了约38%和34%,有效提升了对电离层foF2的预测精度.
2) 电离层foF2重构误差存在较为明显的时间和空间变化规律:在纬度变化上,中纬区域的重构误差低于低纬区域;在年变化上,重构的绝对误差和均方根误差有随太阳活动强度增强而增大的趋势,重构的相对误差在10%上下波动,无明显年变化;在季节变化上,夏季重构误差最小,其他三个季节相差不大;在地方时变化上,白天重构误差低于夜间,且该重构方法有较好的稳定性.
考虑到该重构方法在低纬区域的误差相对较大,后期将进一步优化该方法在低纬区域的精度.此外,由于高纬度区域缺乏观测台站,如何将该方法应用到高纬区域电离层foF2的重构并保证精度,也将是本文下一步研究方向.
致谢:感谢美国马萨诸塞大学洛厄尔分校(UMass Lowell)和全球电离层无线电观测站(Global Ionospheric Radio Observatory, GIRO)的数字测高仪数据库(DIDBase)提供的foF2数据,同时也感谢国内的测高仪台站如SANYA等站.

