辛时域多分辨率算法在波导结构仿真中的应用
李磊 卫敏
(安徽大学电气工程与自动化学院,合肥 230601)
引 言
时域多分辨率(multiresolution time-domain, MRTD)算法是将矩量法(moment of method, MoM) 中的小波伽辽金法和多分辨率分析(multiresolution analysis,MRA)相结合[1-2],电磁场量在空间方向上用尺度函数和小波函数展开处理[3-5],在时间方向上用矩形脉冲函数进行展开. 与时域有限差分(finitedifference time-domain, FDTD)算法相比,具有良好的色散特性,从而可节省计算资源,提高计算效率.但是稳定度较低,对时间步的限制比FDTD算法更加的严苛,也就是“用时间换空间”. 文献[6]提出的交替方向隐式(alternating-direction implicit,ADI)-MRTD算法摆脱了传统MRTD对于稳定性条件的束缚[6],但是其数值色散特性较差. 龙格-库塔(Runge-Kutta, RK)-MRTD算法[7]在保持MRTD算法较好色散特性的同时进一步提高了数值稳定性,提高了计算效率,但该算法是能量耗散的. 本文把辛算法引入传统的MRTD算法中,在空间方向利用小波尺度函数进行离散处理,以获得良好的色散特性,在时间方向利用辛算子进行离散,从而改善MRTD算法对于稳定性条件的限制.
波导结构元器件在微波毫米波通信中具有广泛的应用,多年来波导结构的特性分析一直是电磁工程的重要研究方向. 波导结构主要包括波导内部的不连续(类谐振腔、填充介质、膜片、导体柱等),矩形波导缝隙,脊波导及其缝隙等更加复杂的结构[8]. 矩形波导是波导结构元器件中的典型代表,因此,辛时域多分辨率(symplectic multiresolution time-domain, S-MRTD)算法在矩形波导仿真中的研究,对于分析和理解其他波导结构特性时具有参考意义.
1 S-MRTD算法
1.1 Maxwell方程的Hamilton表示

式中:E是电场强度;H是磁场强度;ε是媒质中的介电常数;µ是媒质中磁导率.
将式(1)写成矩阵形式:

式中: ℜ为3维旋度算子表示形式;算符U和V含有三维旋度算子 ℜ.
1.2 空间离散
在空间方向上对上述方程进行离散,采用MRTD算法将电场与磁场用具有紧支撑的Daubechies小波尺度函数进行展开并代入Maxwell方程组,得到

式中:LS为 基函数的支撑域;a(v)为Daubechies小波尺度函数的连接系数.
1.3 时间离散
在时间方向上,利用辛算法进行离散处理,时间t取值为0~ ∆t时,式(2)的解可表示为

由于指数算符 exp(∆t(U+V))并不能显式计算,式(7) 仅仅是形式解,因此,采用辛积分传播子[9]得到 exp(∆t(U+V))的m级p阶近似展开为
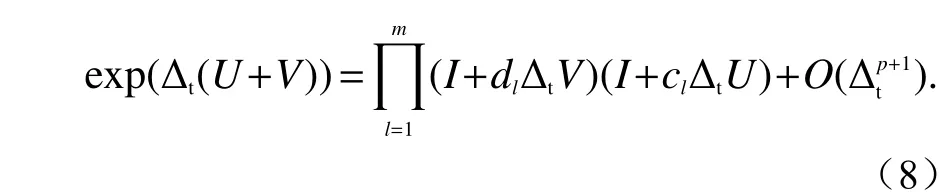
式中:m,p(m≥p)分别为辛积分传播子的近似级数与阶数;cl,dl分别为辛积分传播子系数,其取值如表1所示.
中国作为贸易出口大国,主要特征之一就是出口商品结构低级化。高铁涉及众多产业及技术,中国高铁走出国门,就能在极大程度上改善现状,带动大量产业迅速发展,实现技术上的不断突破。另外,庞大的市场必将造就一批拥有高端技术资金雄厚的国际化企业,带动包括高铁在内的一批高科技产品的对外输出,推动我国出口产品的转型,高端产品将代替低端技术、低端商品进入国际市场,推进中国出口贸易由产品贸易向技术贸易的转型,有助于“中国制造”向“中国创造”转变,影响深远。

表1 辛积分传播子系数Tab. 1 The coecients of symplectic integrator propagator
从式(8)可以看出,辛算法具有显式逐级递推的特点. 因此,同隐式算法和RK-MRTD算法相比,能够有效节省计算资源,提高计算效率.
在空间方向和时间方向分别利用MRTD算法、辛积分传播子算法离散后,建立了Maxwell方程的离散辛框架,即S-MRTD算法.
为了减少因为电场和磁场幅度差异引起的误差,经过如下归一化处理:

归一化后电场和磁场x方向上的迭代公式如下:

式中:

2 数值稳定特性和数值色散特性分析
2.1 数值稳定性分析
在文献[10-11]中详细分析了5级4阶的SMRTD算法稳定特性,为了简单起见,在均匀离散的情况,即∆x=∆y=∆z=∆时,稳定性常数可以定义为

CFLmax称为最大稳定性常数. 在算法的使用中,稳定性常数的选取不能超过最大稳定性常数,否则会造成程序的不稳定,数值计算结果出现发散. 基于D2小波尺度函数S-MRTD算法的最大稳定数常数列于表2中,为了能更好地对比S-MRTD算法对于稳定性条件的改善,基于D2小波尺度函数MRTD算法的最大稳定数常数也列在表2中. 从表2可以看出,相对于5级4阶辛算子,优化的3级3阶辛算子[12-13]对于算法的数值稳定特性有明显的改善.

表2 MRTD算法的最大稳定性常数Tab. 2 The CFLmax number of MRTD method
2.2 数值色散特性分析
使用统一的空间步,稳定性常数取CFL=0.4来绘制色散曲线. 图1(a)为算法相对相速度误差随空间分辨率(points per wavelength, PPW)的变化,图1(b)为算法相对相速度误差随稳定性常数的变化,其中平面波的入射角度为 θ=60◦,φ=45◦.

图1 相对相速度误差随PPW和CFL变化Fig. 1 Relative phase-velocity error vs. PPW and CFL
从图1(a)可以发现,3级3阶的S-MRTD算法和5级4阶的S-MRTD算法都具有良好数值色散特性,几乎和RK-MRTD算法相当,明显比ADI-MRTD算法和MRTD算法更为优越,且在相同的计算条件下,S-MRTD算法的数值计算结果精度更高. 从图1(b)可以看到,3级3阶的S-MRTD算法和5级4阶的S-MRTD算法都具有良好的数值稳定特性,同时有比RK-MRTD算法更为宽松的稳定性条件,这明显改善了MRTD算法苛刻的稳定性条件限制,而且在较高的稳定常数条件下,S-MRTD算法也能得到精确的数值计算结果. 由于3阶3级的SMRTD算法相较于5级4阶的S-MRTD算法有更少的时间步,更高的计算效率,故后续算例皆采用3阶3级的S-MRTD算法.
3 数值计算结果与分析
3.1 填充介质的谐振频率
矩形波导谐振腔的结构图同参考文献[1],尺寸a×b×c=1m×2m×1.5m ,空间步长 ∆s=0.25 m,稳定度性数CFL=0.4,时间步长 ∆t=3.3×10−10s,总计算时间步长为50000步,调制脉冲源频谱范围为15~40 MHz,扫描中心频率f0=30 MHz,扫频间隔0.01 MHz. 矩形波导谐振腔的频谱分布如图2所示. 谐振频率的解析解与仿真计算结果见表3,可见S-MRTD算法具有良好的计算精度.

图2 矩形波导谐振腔的频谱分布Fig. 2 Spectrum distribution of rectangular waveguide cavity

表3 谐振频率解析解与仿真结果对比Tab. 3 Comparison between analytical solution of resonance frequency and simulation results
3.2 波导的截止频率
非填充介质WR-3矩形波导,波导的横向尺寸a×b=0.864mm×0.432 mm,空间步长∆s=0.072 mm,稳定性常数CFL=0.4, 时间步长 ∆t=0.096 ps,总计算时间步长为10000步,调制脉冲源频谱范围为170~800 GHz,扫描中心频率f0=475 GHz,扫频间隔为0.5 GHz. 在频谱范围内激励的模式为 T E10、T E01、TE20、TE11(TM11)、TE21(TM21)、TE12(TM12)、TE22(TM22),各激励模式的截止频率如图3所示. 归一化电场能量其峰值对应的频率就是矩形波导的截止频率,从图3可以看出,S-MRTD算法对应的数值截止频率与解析解吻合较好. 在相同误差边界(0.3%)条件下,改变空间步长和CFL,MRTD算法和S-MRTD算法仿真所消耗的内存和CPU时间见表4. 从表4中数据可以看出,S-MRTD算法比MRTD算法大约节省69.1%的内存和58.5%的计算时间.

图3 WR-3矩形波导频谱范围内各激励模式的截止频率Fig. 3 The cut off frequency of rectangular waveguide

表4 两种算法消耗的计算机资源对比Tab. 4 The consumption of 2 computation resources
3.3 填充介质的波导散射参数
部分填充介质的WR-90矩形波导结构如图4所示, 波导横向尺寸a×b=22.86mm×10.16 mm,介质块放置在矩形波导底面上,空间步长∆s=1.27 mm,时间步长 ∆t=1.693 ps,稳定性常数CFL=0.4,总计算时间步长为20000步,调制脉冲源频谱范围为8~13 GHz,扫描中心频率f0=10 GHz,扫频间隔0.03125 GHz. 为了使S-MRTD算法在粗网格和较高的稳定性常数下仍能得到精确的计算结果,参数设置如下:空间步长 ∆s=2.54 mm,稳定性常数CFL=0.75,图5为矩形波导散射参数的数值结果.从图5可以看出,本文计算的散射参数与高阶辛时域有限差分(symplectic finite-difference time-domain,S-FDTD)算法[14]计算结果吻合度很好.

图4 内部填充介质的WR-90矩形波导Fig. 4 WR-90 rectangular waveguide filled with dielectric material

图5 WR-90矩形波导散射参数结果对比Fig. 5 Comparison of scattering parameters of WR-90rectangular waveguide
4 结 论
本文把优化的3级3阶辛算子引入到S-MRTD算法,对其数值稳定性和数值色散特性的分析显示了其对于ADI-MRTD和RK-MRTD算法在数值稳定和数值色散方面的优化特性. 应用该算法对矩形波导结构进行了研究,相关特征参数的数值仿真结果显示了优化S-MRTD算法的正确性,并且消耗更少的CPU时间和计算机内存. S-MRTD算法的引入为波导相关特性的分析提供了新的高效的计算算法.

