大型双锥椭圆笼形天线关键参数的影响分析

朱湘琴 吴伟 王海洋

（强脉冲辐射环境模拟与效应国家重点实验室, 西安 710024）

引 言

电磁脉冲(electromagnetic pulse, EMP)模拟器由于可以为复杂电子系统的效应实验提供EMP环境而获得广泛研究[1-8]. 根据模拟器所提供场的主极化分量的类型，可以将模拟器分为垂直极化和水平极化两种. 目前，国内外已有的水平极化EMP模拟器主要有：基于横电磁(transverse electromagnetic,TEM)喇叭的辐射波天线[1-6]及基于TEM喇叭的有界波天线[7-9]、双锥笼形水平辐射天线[10-14]等. 此外，文献[15-16]提到了一种水平极化的EMP椭圆混合型辐射波模拟器(如美国的TEMPS&AESOP模拟器及HPD模拟器)，这种模拟器建立在地面上方，可以提供自由空间及近地面EMP环境；这种模拟器的外形是将双锥水平笼形天线[11]的笼由水平状改为椭圆状而成，并对构成椭圆笼形的线栅进行了均匀的离散电阻加载. 文献[16]还采用近似解析的方法给出了该模拟器辐射场特征波形的预估，但并没有将这类模拟器关键参数对其辐射场的影响进行深入的模拟分析. 目前国内外公开文献也鲜有这方面的报道.

此外，考虑到EMP椭圆混合型辐射波模拟器通常尺寸比较大(如美国的TEMPS&AESOP模拟器及HPD模拟器分别架高20 m和30 m、长120 m和150 m)，且目前国内外文献对这类模拟器加载的电阻大小、电阻总个数及相邻电阻间距等并没有任何详细介绍，而电阻加载的目的仅仅是为了减小模拟器内的反射[16]，为此，在对这类模拟器关键参数的影响进行深入分析时，可以先不考虑模拟器电阻加载的影响，只对无电阻加载双锥椭圆笼形辐射天线关键参数的辐射特性影响进行模拟分析. 目前，国内还没有这方面的相关研究报道.

考虑到并行时域有限差分(finite-difference timedomain, FDTD)方法一次计算就可以得到整个频段的时域信息，且已被广泛应用于大型EMP模拟器的模拟计算中[8,11,17-18]，故本文将先建立无电阻加载的双锥椭圆笼形辐射天线模型，然后基于并行FDTD方法，研究给出该天线的几个关键参数对其辐射场的影响，并给出规律和机理分析.

1 天线的结构及计算方法

建立在地面上方的无电阻加载的双锥椭圆笼形天线结构如图1所示. 可以看出，该椭圆笼形天线由双锥及椭圆形的笼所构成，天线的锥半径和笼的半径相同，均设为r；双锥尖端与地面的垂直距离(即天线的架高)为h；两个笼与地面相交得到的两个圆圆心的间距(简称“圆心间距”)为L. 此外，设天线的双锥半角均为α，对应的特性阻抗Zc=60ln[ctan(α/2)][19-20]. 当构成天线椭圆形笼的线栅足够密时，可以将椭圆形的笼作为实体金属来处理.

图1 双锥椭圆笼形天线示意图Fig. 1 Configuration of biconical-ellipsoid cage antenna

采用基于MPI平台的并行FDTD方法[21]来分析天线的辐射场. 在激励源的设置上，采用同轴馈电的方式进行馈电[21]，同轴线的馈电阻抗与天线的特性阻抗Zc相同；在吸收边界的设置上，采用单轴各向异性介质完全匹配层(uniaxial perfect matched layer, UPML)吸收边界. 由于天线建在地面上方，因此FDTD计算中会有部分吸收边界与大地相接触，故计算时假设大地为电损耗均匀介质，需对UPML吸收边界特殊处理[22].

截断大地的UPML中电场z分量的FDTD迭代格式如下所示：

式 中：κξ=1+(κmax−1)(lξ/d)m，其 中 ξ=x,y,z，κmax为为UPML吸收边界与大地交界面的最大层数，lξ是ξ方向上UPML层靠近FDTD区的距离，d是UPML介质层的厚度，m是整数，截断大地时取m=20；Hx及Hy分别为UPML中磁场的x分量及y分量，其迭代格式分别与截断无电损耗介质的UPML中磁场对应分量的迭代格式相同[21]；σξ=其中为3个方 向 的 网 格 尺 寸； ε0为 真 空 中 的 介 电 系 数； εr为 与UPML内边界相接触的大地的相对介电系数； σ为其电导率. UPML中电场其他两个分量的FDTD迭代与上述类似.

2 关键参数对辐射场的影响分析

影响双锥椭圆笼形天线辐射场的可能因素有很多，下面将重点考虑椭圆形笼半径r、双锥半角α、架高h、圆心间距L及激励源半高宽(the full width at half maximum, FWHM)tw对天线辐射场的影响.

2.1 不同椭圆形笼半径的影响

设图1所示的双锥椭圆笼形天线的架高h=15 m，圆心间距L=61.118 m，天线的双锥半角α=32°. 天线采用同轴激励的方式进行激励. 激励电压源为双指数脉冲，其表达式为

取U0=2.602×105V、γ=4.0×107s−1及β=6.0×108s−1，得到激励电压的峰值为200 kV，上升前沿为2.5 ns，tw=23 ns. 使用并行FDTD算法进行计算时，取网格尺寸δx=δy=δz=0.036 m. 设天线下方大地的相对介电常数εr=10，电导率σ=0.01 S/m. 在距离地面hd=1 m的水平面上(如图1所示)，分别选择P1(0, 14, 0) m、P2(15, 14, 0) m、P3(15, 14, 12) m及P4(0, 14, 12) m 4个点为监测点；并在这4个监测点的正上方，距离地面hd=5 m的水平面上选择点、点、点及点为监测点. 设椭圆形笼的半径r分别取3.0 m、3.5 m、4.0 m及4.5 m，对应的上述各测点的清晰时间[11]，以及测点电场z分量(Ez)的峰值、上升沿和FWHM(后续分别简称为场的峰值、场的上升沿和场的FWHM)分别如表1和表2所示.

表1hd=1 m的水平面上4个测点的清晰时间以及Ez的峰值、上升沿和FWHMTab. 1 Clear-time at 4 testing points, and the peak-value, rise-time and FWHM of Ez in the horizontal plane hd=1 m

表2hd=5 m的水平面上4个测点的清晰时间以及Ez的峰值、上升沿和FWHMTab. 2 Clear-time at 4 testing points, and the peak-value, rise-time and FWHM of Ez in the horizontal plane hd=5 m

由表1可以看出，在距离地面1 m高的水平面上：

1) 椭圆形笼的半径r从3.0 m增加到4.5 m时，P1点及P2点场的峰值的最大相对差均小于0.3%，即这两个测点场的峰值受半径r的影响比较小；P3点场的峰值随着r的增大先增加，后趋于不变；P4点场的峰值随着r的增大而增大.

根据P1点、P2点、P3点及P4点的位置，可以估算出大地对这几个测点场作用的最短光程与激励源对这几个测点场作用的最短光程之差分别为6.67 ns、5.65 ns、5.34 ns及5.90 ns. 据此，结合激励源的峰值出现时间4.81 ns，可以预估天线下方的大地对上述4个测点场的峰值影响比较小. 另一方面，双锥椭圆笼形天线中双锥的长度为有限长度，其与椭圆形笼之间的连接处对测点场峰值的影响可以通过清晰时间表征. 当椭圆笼的半径r从3.0 m增加到4.5 m时，P1点及P2点的清晰时间分别都大于这两个测点场的峰值出现时间，而P4点的清晰时间则小于该测点场峰值出现的时间. 这就导致双锥干涉不会影响P1点及P2点场的峰值，椭圆形笼半径(即双锥锥底的半径)的变化不会影响P1点及P2点场的峰值，但会引起P4点场峰值的改变；且当笼的半径r越大时，椭圆形笼的辐射能力越强，因此P4点场峰值会随着r的增大而增大.

此外，与P4点类似，当r从3.0 m增加到4.0 m时，P3点的清晰时间均小于测点场峰值出现的时间，故r从3.0 m增加到4.0 m会引起P3点场的峰值增加. 但当r=4.0 m及4.5 m时，P3点对应的清晰时间分别为4.71 ns及5.57 ns，前者接近峰值出现的时间，后者大于峰值出现的时间，故当r=4.0 m及4.5 m时，P3点场的峰值差别不是很大.

2) 无论r取何值，P1点场的峰值最大. 这是由于P1点距离馈源最近，且该测点的清晰时间大于测点场峰值出现的时间(即场的峰值不受双锥干涉的影响).

3)r从3.0 m增加到4.5 m时，P1点场的上升沿的最大相对差小于2.5%，P2点场的上升沿基本保持不变，即上述两个测点场的上升沿受半径r的影响比较小. 而r从3.0 m增加到4.0 m时P3和P4点场的上升沿均发生变化.

根据1)的分析可知，当椭圆笼的半径r从3.0 m增加到4.5 m时，P1点及P2点的清晰时间分别大于这两个测点场的峰值出现时间；而r从3.0 m增加到4.0 m及r从3.0 m增加到4.5 m时，对应的P3点及P4点的清晰时间均小于该测点场峰值出现时间. 当测点的清晰时间大于测点场峰值出现时间时，不会对测点场的上升沿造成干扰，反之则会影响测点场上升沿的读取. 理论分析与模拟结果一致.

4)r从3.0 m增加到4.5 m时，P1点、P2点、P3点及P4点场的FWHM均小于激励源的FWHM.根据1)中估算出的大地对这几个测点场作用的最短光程与激励源对这几个测点场作用的最短光程之差，以及激励源的FWHM可知，天线下方的大地对P1点、P2点、P3点及P4点场的FWHM有影响，即地面反射的存在，导致上述4个测点场的FWHM减小.

由表2可以看出，在距离地面5 m高的水平面上：

1) 椭圆形笼的半径r从3.0 m增加到4.5 m时，点及点场峰值的最大相对差分别小于0.4%及0.2%，即这两个测点场的峰值受r的影响比较小；而点及点场的峰值随着r的增大而增大.

2) 当r从3.0 m增加到4.5 m时，点场上升沿的最大相对差小于2.4%，点场的上升沿基本不变，即这两个测点场的上升沿受椭圆笼半径r的影响比较小；点及点场的上升沿均发生变化.

3)当r从3.0 m增加到4.5 m时，点和点场的FWHM随r的增加而变宽；点场的FWHM随r的增大而变窄.

此外，对比表1和表2可知，1) 椭圆形笼的半径r从3.0 m增加到4.5 m时，半径的大小对P1点和P2点及这两个测点上方水平面上对应的P1′点和P2′点场的峰值和上升沿影响不大，这是由于这几个测点的清晰时间大于测点场峰值出现时间的缘故. 而P4点及点场的峰值随着r的增大而增大，这是由于这两个测点的清晰时间过小导致测点场的峰值受半径影响比较大的缘故. 2) 不管r取何值，P1点及其上方水平面上对应的点场的峰值在所属的水平面上最大，这是由于测点距离激励源最近的缘故. 3) 不管r取何值，距离地面5 m的水平面上的测点场的FWHM明显大于距离地面1 m的水平面上的对应测点. 这是由于距离地面1 m的水平面上的测点场的FWHM受地面影响的缘故.采用本文所述的模拟方法，模拟得到不同椭圆形笼半径r时，上述4个测点场随时间的变化如图2所示.

图2 天线半径不同时4个测点Ez的时域波形的比较Fig. 2 Comparison of Ez at 4 testing points as the antenna with different radii

对应表1和表2所示测点的清晰时间，从图2(a)及图2(c)可以看出：当清晰时间大于测点脉冲峰值出现时间时，测点场的峰值和上升沿受椭圆形笼半径的影响比较小，但脉冲的后延会受到影响；反之，若清晰时间小于测点脉冲峰值出现时间，则会使得测点场的峰值受到影响，如图2(b)及图2(d)所示.

2.2 不同双锥半角的影响

双锥椭圆笼形天线的架高h、圆心间距L、天线的激励源及天线下方大地的介质参数均与2.1节相同，设椭圆形笼的半径r=3.5 m，分别取双锥半角α=22°、32°及42°，对应的双锥天线的特性阻抗分别为196 Ω、150 Ω及115 Ω. 根据模拟，得到双锥半角α不同时距离地面5 m高的水平面上4个测点点、点、点及点电场z分量Ez随时间的变化如图3所示. 对应地，表3给出了上述测点的清晰时间以及场的峰值、上升沿和FWHM.

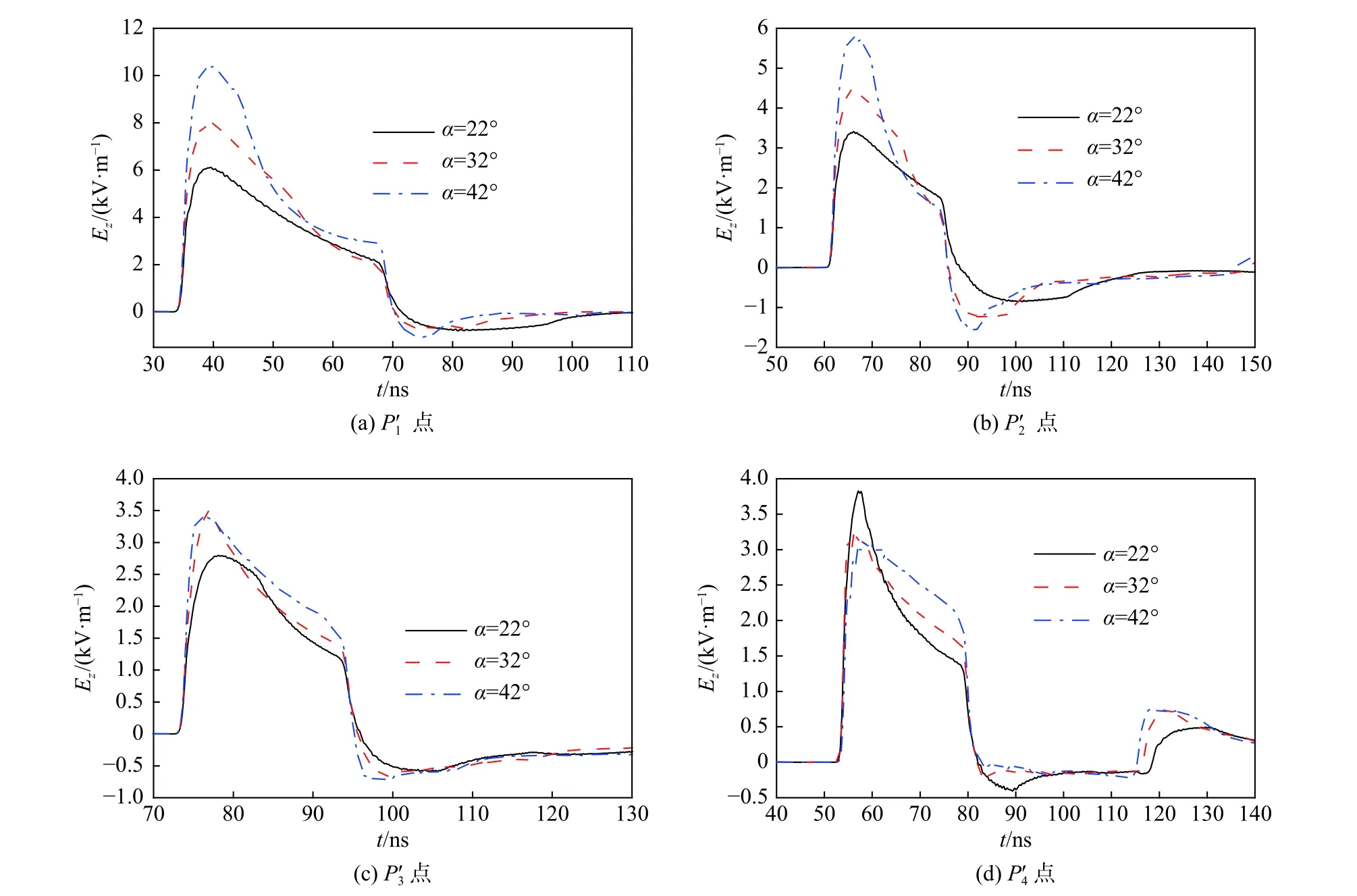
图3 天线双锥半角α不同时4个测点Ez的时域波形的比较Fig. 3 Comparison of Ez at 4 testing points as the antenna varies with different α

表3 双锥半角不同时4个测点的清晰时间以及Ez的峰值、上升沿和FWHMTab. 3 Clear-time at 4 testing points, and the peak-value, rise-time and FWHM of Ez as the antenna with different α

从图3和表3可以看出：

当保持双锥的锥底半径r不变，随着双锥半角α的增大，双锥的金属沿面减小，双锥低频辐射能力减弱，会使得从双锥流向椭圆形笼的电流增加，从而导致椭圆形笼的低频辐射能力增强，引起其正下方的点场的FWHM的增加.

考虑到天线的双锥半角直接影响了天线辐射区场的峰值、上升沿和FWHM，因此，需要根据工程实际选择合适的双锥半角.

2.3 不同架高的影响

双锥椭圆形天线的圆心间距L、椭圆形笼的半径r、双锥半角α、天线的激励源参数及天线下方的大地介质参数均与2.1节相同. 分别取天线的架高h=10 m、15 m及20 m，根据模拟得到位于距离地面5 m的水平面上的 点场的峰值分别约为16006 V/m、8040.04 V/m及5322.26 V/m. 这是由于激励源峰值电压不变时，架高越高，测点距离激励源更远的缘故. 以点场的峰值为归一化因子，给出天线架高不同时距离地面5 m的测试平面上42 m (x方向)×28 m (z方向)的范围内Ez的归一化峰值分布如图4所示.

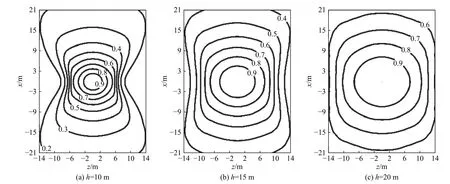
图4 天线架高不同时距离地面5 m的水平面上归一化Ez峰值分布比较Fig. 4 Normalized Ez on horizontal plane hd=5 m as the antenna with different h

从图4可以看出，天线架高越高，上述区域内场的分布越均匀，即与地面距离相同的水平面上的辐射场的均匀性越好. 这是由于天线架高越高，距离地面5 m的测试平面距离激励源越远，激励源到测试平面上的各测点的光程之差越小的缘故.

2.4 不同圆心间距的影响

双锥椭圆笼形天线的架高h、椭圆形笼的半径r、双锥半角α、天线的激励源参数及天线下方的大地介质参数均与2.1节相同. 分别取天线圆心间距L=51.118 m、61.118 m及67.118 m进行模拟.当取L=67.118 m时，整个FDTD计算区域的网格数约为23.8亿. 与2.3节类似，以点场的峰值为归一化因子，模拟给出yoz剖面上y方向距离地面1～5 m、z方向40 m的范围内归一化Ez峰值分布如图5所示. 可以看出，当天线圆心间距L越大时，上述测试区平面内|z|＞15 m的边缘处的场更均匀.这是由于L越小时，测试区边缘的测点越靠近椭圆形的金属笼，从而造成测试区边缘处场的畸变，使得场的均匀性受到影响.

图5 天线L不同时yoz剖面上归一化Ez峰值分布Fig. 5 Normalized Ez on yoz plane as the antenna with different L

2.5 激励源FWHM的影响

从2.1节和2.2节的模拟分析可知，椭圆形笼的半径r及双锥半角α的改变对距离地面5 m的水平面上的测点及响，但对这两个测点场的FWHM影响比较大，故分析激励电压源的FWHM对固定平面上测点场FWHM的影响. 设双锥椭圆笼形天线的架高h、圆心间距L、椭圆形笼的半径r、双锥半角α及天线下方的大地介质参数均与2.1节相同. 保持天线激励电压的峰值200 kV及上升前沿2.5 ns不变，模拟场的上升沿几乎没有影给出激励源FWHM从15 ns增加到56 ns时点及点场的FWHM变化如图6所示. 作为比较，图中还给了与这两点在同一水平面上的点及点场的FWHM变化.

图6 激励源FWHM不同时测点Ez 的FWHM变化Fig. 6 FWHM of Ez at several points with different FWHM

从图6可知，当激励源上升沿不变而FWHM增加时，上述4个测点场的FWHM也随之增加，但不是线性增加，有变缓的趋势出现. 特别是点及点，当激励源FWHM分别达到约40 ns及31 ns之后，这两个点场的FWHM受激励源FWHM的影响不是很明显.点及点场FWHM的非线性增加，主要是受双锥与椭圆形笼接头处(即清晰时间)的影响；而点及点场的FWHM除了受上述接头处影响外，还受到地面反射的影响.

3 结 论

本文基于并行FDTD方法研究分析了双指数脉冲激励的、位于地面上的大型双锥椭圆笼形天线的辐射场特性. 先建立天线同轴线馈电，然后模拟分析了天线的椭圆形笼半径、双锥半角、架高及圆心间距等几个关键参数对该天线辐射场的影响，给出了对应的机理分析. 本文所述理论对双锥椭圆笼形天线模拟器的工程设计具有一定的参考价值.