基于关节速度的液压比例驱动工程机械臂位姿控制

高 波，王珞豪

(山东科技大学 电气与自动化工程学院，山东 青岛 266590)

引言

工程机械是我国的重要产业之一，广泛应用于道路、建筑、矿山和水利等工程领域，是生产、建设的重要工程设备[1-2]。液压比例阀控系统拥有结构简单、输出力矩大、可靠性较高、响应快、传动效率及控制精度高等优点[3]。负载敏感系统具有效率高、体积小且结构紧凑等优点，并能对系统流量与压力关系实现自动控制，广泛应用于工程机械[4-5]，因此使用负载敏感液压比例阀控系统驱动机械臂关节。

由于阀控液压缸系统完成的是一个直线运动，伺服系统中常采用精度较高的位置传感器测出位置。但在实际工程机械应用中，在比例阀控缸安装位置传感器会使得系统复杂，可靠性与效率降低。一些工程机械尝试用倾角传感器获得部分关节的姿态并加以控制，取得了较好的效果，但局限性较大，只适用于少数应用。

为解决这个问题，本研究基于对机器人正逆运动学、阀控液压缸控制、陀螺仪姿态解算进行研究分析，实现机械臂位姿闭环控制，从而可以取代阀控液压系统位置闭环伺服控制。由此基础上通过MATLAB/Simulink软件实现基于关节速度控制的比例液压系统驱动机械臂闭环控制建模，仿真并验证方法的合理性和可行性。

1 工程机械臂机器人学分析

1.1 正运动学分析

对液压驱动机械臂位姿控制之前，需要进行必要的运动学分析，求得各关节连杆坐标变换关系以及机械手的运动学正解和逆解。使用D-H法建立机器人运动学模型，该方法通过4个参数连杆长度ai、连杆扭转角αi、连杆偏距di、关节角θi来描述机器人相邻连杆之间的位姿关系，进而建立机器人模型。本研究以喷浆机械臂为例[6]，各关节均采用摆动关节，取代原先为便于操控而设置的伸缩关节，使其结构更为优化，建立连杆坐标系如图1所示。根据连杆坐标系，可得各连杆坐标参数如表1所示。

图1 喷浆机械臂连杆坐标系

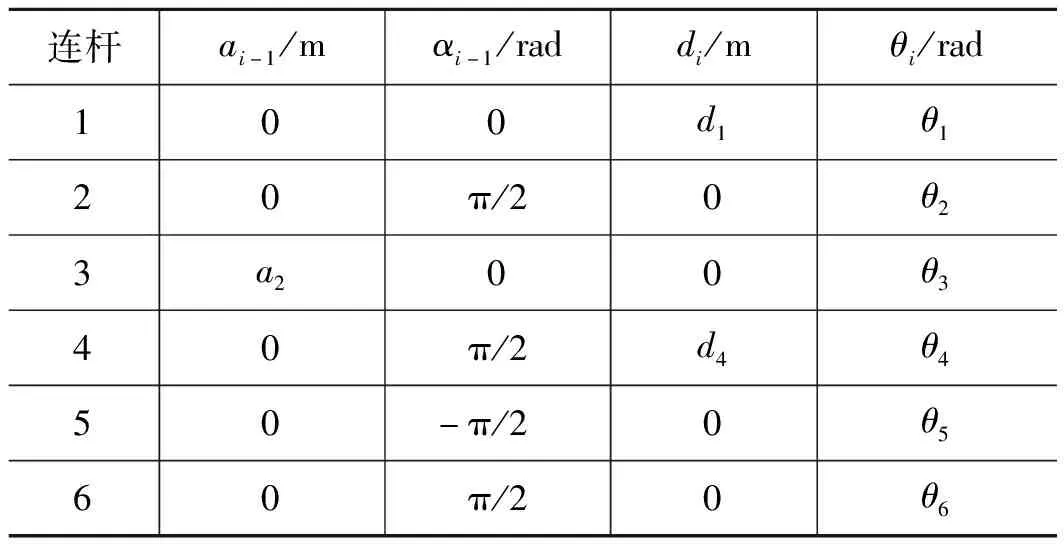
表1 喷浆机械臂D-H参数

其中d1=0.5，a2=2，d4=2。根据表1的各连杆参数，由连杆变换矩阵式(1)得到各连杆的变换矩阵：

Ai=

(1)

由此得出正运动学模型，机械臂末端坐标系相对于基坐标系的位姿变换矩阵如式(2):

(2)

使用MATLAB中的机器人工具箱构建机械臂仿真，验证了机械臂正运动学模型的正确性，为后面进行逆运动学分析奠定了基础。

1.2 逆运动学分析

逆运动学是由已知的机械臂末端位姿，计算机械臂的各关节变量，本研究采用代数法求逆解。

由于三轴加速度计在工程机械实际应用中受限于技术水平而导致累积误差较大。超高精度的捷联惯导系统位置累积误差仍可达到10 cm/h，因此对于本研究的六关节机械臂，选择使用2个陀螺仪分别装于关节3与关节6处获取姿态信息。关节3处的姿态信息用于对关节角θ1，θ2，θ3进行解算，关节6处的姿态信息结合前3个关节信息可以实现对θ4，θ5，θ6的解算，由此完成机械臂逆运动学分析。

1.3 陀螺仪姿态解算

陀螺仪能够通过测量载体运动角速度解算得出偏航角、俯仰角与滚转角获取姿态信息[7]。在进行机器人姿态解算时，本研究采用四元数算法[8]对姿态矩阵进行求解，通过四元数的变化对姿态矩阵进行更新，通过式(3)求得四元数：

式中，ωbx，ωby，ωbz由陀螺仪输出计算得到的角速度信息，利用式(3)求得的四元数表示为姿态矩阵，如式(4):

C=

(4)

由式(4)可得关节3处的姿态矩阵C3与关节6处的姿态矩阵C6：

(5)

(6)

1.4 逆运动学求解

1)求解关节角θ1，θ2，θ3

由于工程机械臂在结构上θ2与θ3同为俯仰角且轴线在同一平面内，故θ3处陀螺仪所测得同一姿态下θ2，θ3逆解时出现多解，为避免这个问题，本研究在θ2处安装一个倾角传感器输出θ2的值；也可对机械臂关节设计进行优化，避免出现这种冲突，如调换关节3和关节4，但如何优化效果最佳及其数学表达仍待进一步研究。

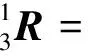
(7)

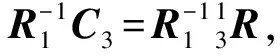
(8)

(9)

式中,C11，C13，C21，C23，C31为式(5)中矩阵C3的各个元素，由式(8)、式(9)可解得关节1、关节3的值θ1，θ3。

2)求解关节角θ4，θ5，θ6

(10)

(11)

式中,

r13=azsin(θ2+θ3)+axcos(θ2+θ3)cosθ1+

aycos(θ2+θ3)sinθ1

(12)

r23=azcos(θ2+θ3)-axsin(θ2+θ3)cosθ1-

aysin(θ2+θ3)sinθ1

(13)

r33=axsinθ1-aycosθ1

(14)

r21=nzcos(θ2+θ3)-nxsin(θ2+θ3)cosθ1-

nysin(θ2+θ3)sinθ1

(15)

r22=ozcos(θ2+θ3)-oxsin(θ2+θ3)cosθ1-

oysin(θ2+θ3)sinθ1

(16)

上式中ni，oi，ai为式(6)矩阵C6中各个元素，令式(10)、式(11)两矩阵的元素(1,3)、(2,1)、(2,2)、(2,3)、(3,3)对应相等可解得：

(17)

θ4=atan 2(r33,r13)

(18)

θ6=atan 2(-r22,r21)

(19)

由此根据已知陀螺仪解算的姿态矩阵可逆解求得各个关节的角度值，且机械臂末端位置也可通过正运动学一并解出，据此可实现位姿闭环以获得各关节速度给定值。

2 位姿闭环控制模型

工程机械臂的各关节通过负载敏感比例阀控液压系统驱动。负载敏感液压系统是一种根据系统压及流量需求动态调整提供所需求的流量和压力大小的液压回路[10]，使执行元件的速度仅与比例换向阀开度有关，而与负载压力无关。电磁比例阀是液压系统的流控元件，响应速度快且控制方便[11]。从而根据本研究内容建立电磁比例阀控液压开环系统，如图2所示。

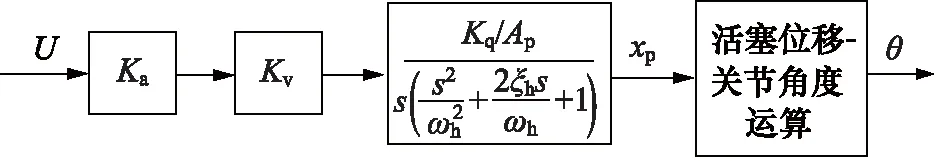
图2 比例阀控液压油缸数学模型

图2中，Ka(A/V)为PWM比例放大器比例系数；Kv为电磁比例阀流量增益，m3·A/s；Kq为阀的空载流量增益，m3·A/s；Ap为活塞有效作用面积，m2；ωh为液压固有频率；ζh为液压阻尼比[12]。

通过对阀控液压系统综合设计分析，其开环传递函数可以近似为：

(20)

连杆与液压缸不同的结构组合会使活塞位移与连杆间角度变换关系发生变化，本研究中液压油缸驱动喷浆机器人大臂、小臂关节的原理如图3所示[13]。

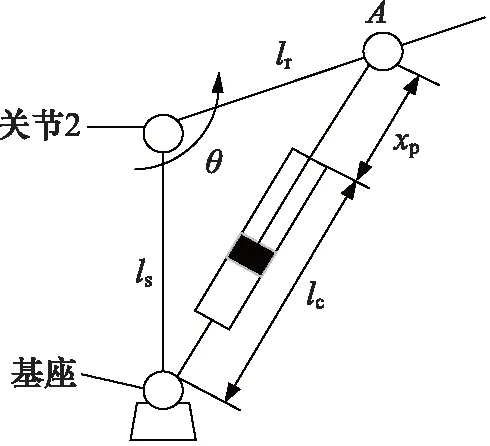
图3 液压驱动关节原理

图3中，ls为关节2与基座间的距离；lr为油缸与大臂连接处A至关节2间的距离；xp为油缸活塞位移；lc为油缸长度；θ为两连杆间的角度。根据图3由余弦定理计算可得，液压缸活塞位移与连杆间角度变换关系为：

(21)

通过对液压缸模型与机器人运动学的分析，可构建出位姿闭环控制总框图，如图4所示。

由图4可知，输入由目标位姿T逆解得到的各关节目标角度θT，同时通过装于机械臂的陀螺仪测出当前姿态，利用逆解算法解算出当前的各关节角度值θd，与目标关节角θT进行比较，以此偏差值进行调节控制，其输出作为关节速度信号给定输入到阀控液压系统，实现对机械臂的位姿调整，最终完成位姿闭环控制。也可以直接用位姿误差根据雅可比方程求解关节速度给定量，但是这种方法需要实时计算机器人逆雅可比矩阵，结构复杂且计算量大，影响系统实时性[14]。

图4 喷浆机械臂位姿闭环控制框图

3 闭环控制仿真

3.1 仿真模型构建

利用MATLAB的机器人工具箱对机器人进行运动学仿真并对建模的正确性进行验证。利用表1所列的D-H参数建立喷浆机械手模型。

根据第2节所述的闭环控制框图，通过 MATLAB/Simulink建立关节速度控制的液压驱动机械臂位姿闭环控制模型，仿真框图如图5所示。

1.目标关节角 2.比例增益 3.液压缸模型 4.机械臂模型 5.逆运动学解算模块 6.正运动学解算模块 7.末端姿态输出 8.末端位置输出

倾角传感器输出的θ2值与陀螺仪输出姿态矩阵C3，C6输入到逆运动学解算函数模块中，其输出的关节值通过正运动学解算模块得出当前机械臂末端位姿，同时与输入的目标值进行比较，通过控制器将关节速度量输入到液压油缸模型中，进而输入到由Simulink构建的机械臂模型中对位姿进行调整，实现整个闭环控制仿真。

3.2 闭环控制仿真验证

使用MATLAB/Simulink进行仿真，设置机械臂初始关节位置、目标关节位置,由于关节3结构原因，故设置关节3初始值小于0，具体仿真结果如表2所示。设陀螺仪漂移误差0.01(°)/h，陀螺仪白噪声背离标准0.01(°)/h,采样频率设置为100 Hz。设置θ1，θ4，θ5，θ6关节角速度不超过0.3 rad/s,大臂关节角θ2、小臂关节角θ3关节速度限定不超过0.2 rad/s。根据以上参数得到机械臂末端位姿、各关节角度值、速度变化仿真曲线以及陀螺仪测量值变化仿真曲线如图6、图7所示。

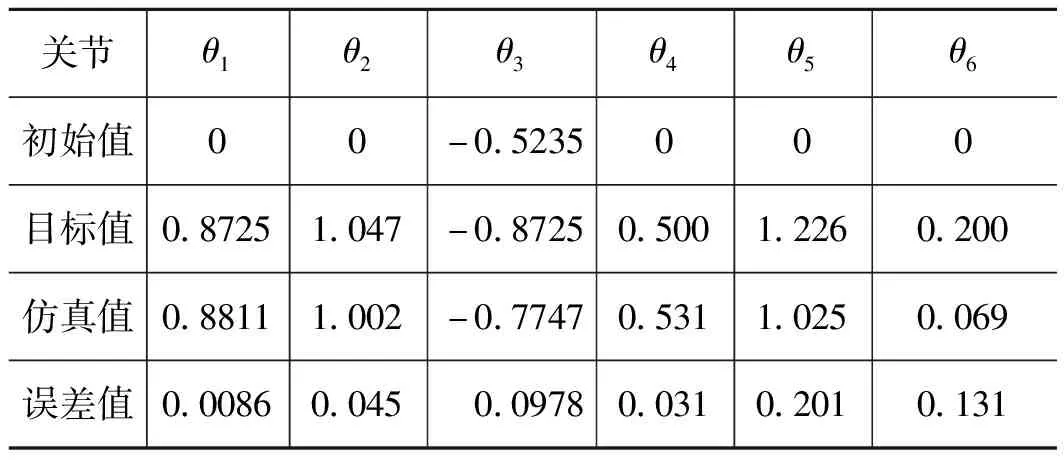
表2 喷浆机器人闭环仿真关节参数 rad/s

图7 陀螺仪测量值仿真

1)陀螺仪测量仿真

在引入漂移误差与白噪声后，对姿态角测量误差进行仿真，结果如图6所示。

陀螺漂移是惯导系统的主要误差源，会激励舒勒周期振荡、地球周期振荡及傅科周期振荡[15]。从图6结果曲线分析，陀螺仪测量误差呈现振荡特性。横滚角、俯仰角、航向角测量误差的标准差分别为0.0017，0.0023，0.0014 rad/s，变化趋势稳定。

关节3处与关节6处陀螺仪测量值仿真如图7所示。陀螺仪测量信号为角速度量，由图7可知关节3与关节6处陀螺仪测量值在仿真时间内趋近于0达到稳定状态。

2)位姿精度分析

由于陀螺仪输出包含了随机误差、噪声误差、漂移误差等，在实际应用中会对姿态角的解算造成影响。根据仿真过程中陀螺仪的输出数据，解算得到位姿测量轨迹，将其与位姿标准轨迹进行对比分析。姿态角变化及误差如图8所示。

从图8的姿态角误差变化可知，横滚角α、俯仰角β、航向角γ误差Eα，Eβ，Eγ最大值为0.167，0.028，0.103 rad，仿真时间内最终姿态相对误差角分别为-0.083，0.034，-0.028 rad，曲线基本呈稳定趋势，且满足精度要求。

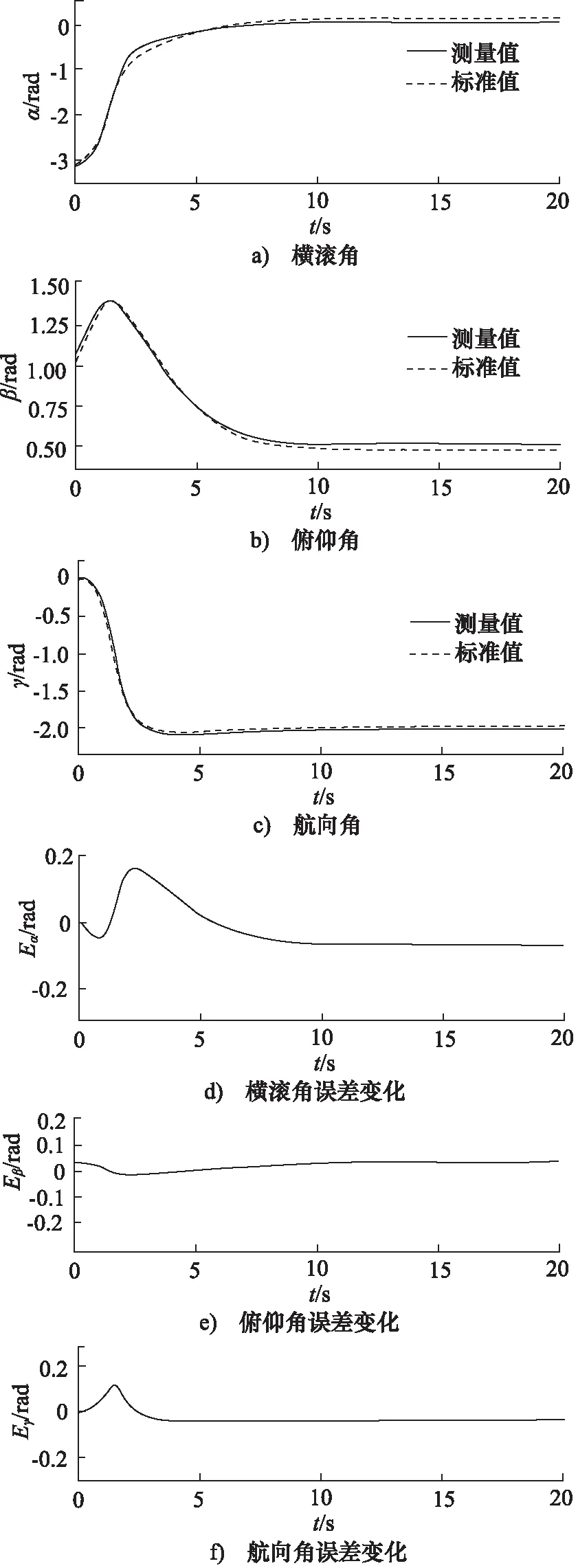
图8 姿态角及其误差变化

末端位置变化及误差如图9所示。将仿真解算的末端位置分量与标准值进行对比分析，X，Y，Z定位误差最大值为0.026，0.036，0.096 m，仿真结果误差Ex,Ey,Ez分别为0.014，-0.027，0.056 m，满足设计精度要求，并能够较稳定的跟踪标准轨迹。综合对位姿误差分析可知，陀螺仪测量误差会对位姿解算精度造成影响，但误差值在精度要求范围内，误差对系统稳定性的影响由以下仿真给出。

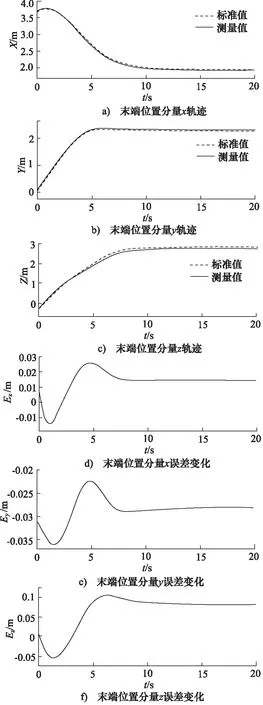
图9 末端位置及其误差变化

3)机械臂参数仿真

机械臂关节速度及误差变化仿真控制结果如图10所示。由关节速度曲线图10a、图10b可知液压驱动机械臂各关节值变化曲线平滑，各关节在速度限定范围内运动并最终收敛到0达到稳定状态。由误差曲线图10c、图10d可知各关节变化与目标值误差在仿真时间内不断减小并趋于稳定，角度参数的跟踪误差如表2所示，其控制精度满足要求。

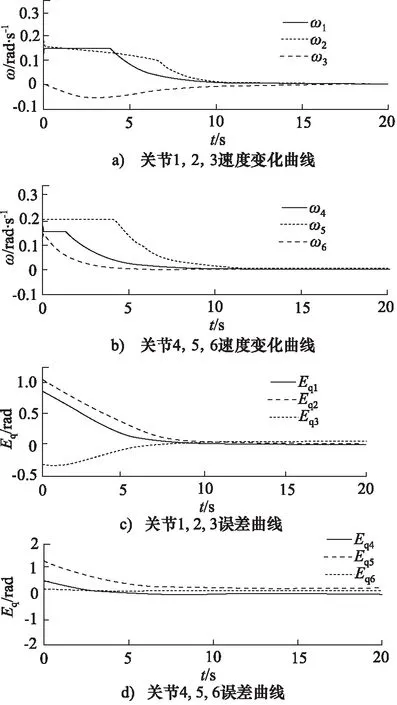
图10 各关节速度、误差变化曲线

末端位姿速度变化曲线如图11所示。液压驱动机械臂位姿闭环控制系统响应时间为20 s，机械臂末端在仿真运动过程中位姿速度变化曲线逐渐趋向于零保持稳定。在2个陀螺仪与1个倾角传感器联合定位下，结合机器人正逆运动学，所建立的液压驱动机械臂位姿闭环控制系统能相对稳定的达到仿真目标要求，输出结果与目标基本一致，验证了方法的可行性。

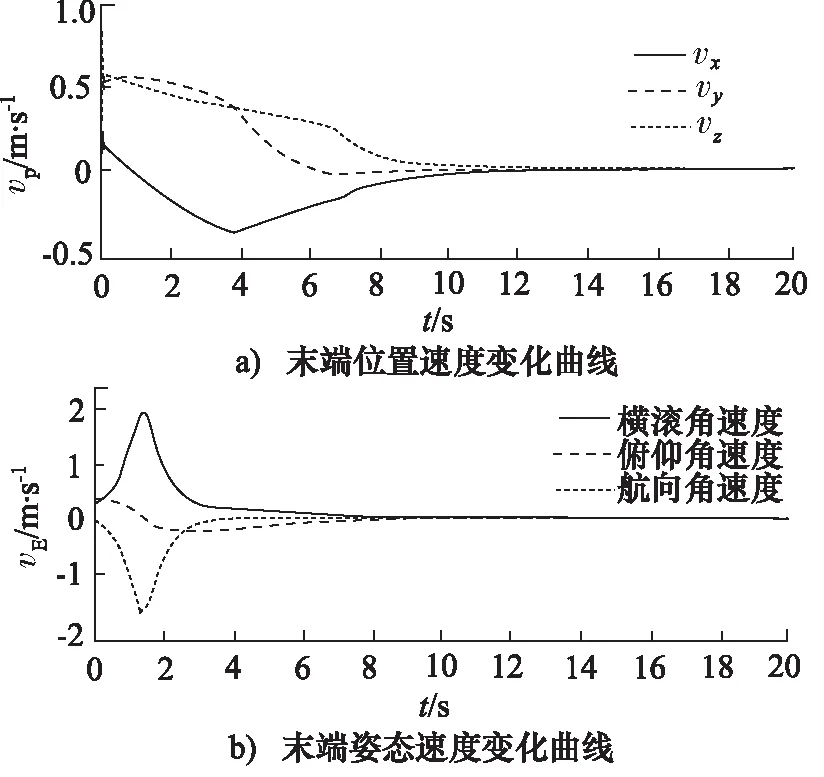
图11 机械臂末端位姿速度变化曲线

4 结论

针对在工程机械上液压系统因加装位置传感器而致使系统复杂的问题，本研究用机器人位姿闭环控制取代了液压系统中的位置闭环，并对于工程作业下惯导系统的加速度计误差较大的问题，使用误差较小陀螺仪解决机械手并采用激光雷达对其累积误差进行修正。运用机器人正逆运动学知识，分析了工程机械臂关节变量和末端执行器位姿之间的坐标变换关系，解决了机械臂运动学方程的建立以及由末端姿态逆解出各关节角的问题并建立了比例控制液压缸数学模型。利用MATLAB/Simulink进行建模仿真，得到各参数的曲线和数据，仿真结果表明了该控制系统的可行性。本研究对于液压驱动工程机械臂位姿闭环控制具有一定参考意义。此外，课题还存在待解决的问题需要进一步研究：

(1)高精度光纤陀螺仪的微型化；

(2)机器人关节布置的优化以及位姿解算的进一步数学分析。；

(3)位姿闭环处控制方法的研究。