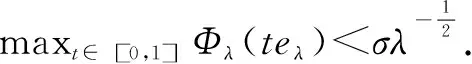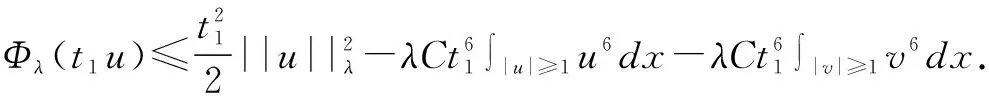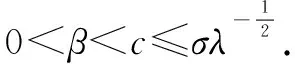一类临界的拟线性薛定谔方程组基态解的存在性
董 楠 王丽丽
(吉林省通化师范学院 134001)
本文主要在R3中研究耦合的拟线性薛定谔方程组
基态解的存在性,其中p,q≥2,4 拟线性薛定谔方程有着深厚的物理背景,具体可参考文献[1]-[3].近年来关于拟线性薛定谔方程组的研究有很多,本文参考文献[4]-[6].定义希尔伯特空间 假设以下条件成立,其中i=1,2: (V1)Vi∈C(R3)且存在常数b>0,使得m{x∈R3:Vi(x) (V2)0=Vi(0)≤Vi(x)≤maxVi. (K)0 定理1.1 假设(V1)-(V2),(K)成立.那么对∀σ>0,∃τσ>0,使得当ε≤τσ时,方程组(1)至少有一个正解uε∈(uε,vε). 令λ=ε-2,则对于λ→+,方程组(1)等价于 因此,对于∀λ>0,范数||·||等价于如下范数 方程组(2)对应的能量泛函为 利用变量替换u:=f-1(u1),v:=f-1(v1),其中f为如下定义 且f(t)=-f(-t),t∈(-,0]. 函数f的性质参看文献[7].变量变化后的能量泛函为 根据假设(V1)和(K)知Φλ为C1的且在E上有意义. 引理3.1 假设(V1)-(V2)和(K)成立.设(un)是泛函Φλ的(P.S.)c序列,则c≥0,且(un)在E中有界. 证明设(un)是一个(P.S.)c序列: 根据(K)及4 (3) 又由(K)和(V2)及函数f的性质可得 从而有 引理3.2假设(un)是引理3.1中定义的.则 因此,我们得到 引理4.1存在ρ,α>0,使得当||u||λ=ρ时,有 引理4.2 对于上述ρ,存在一个常数β>0,使得inf||u||λ=ρΦλ(u)≥β. 显然,对于任意的ε>0,存在Cε>0,使得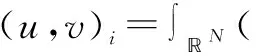
一、等价变分问题
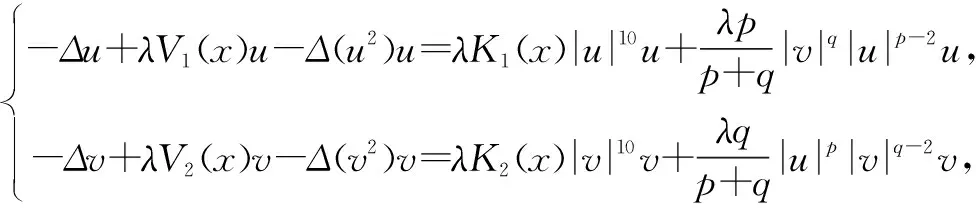
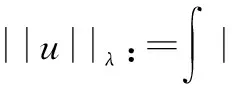
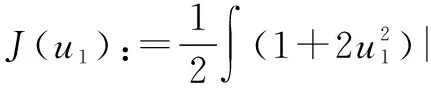
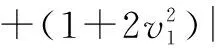
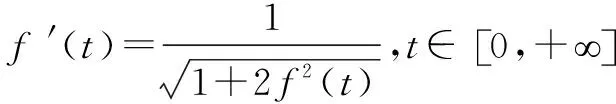
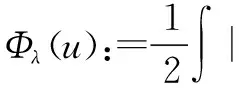
二、(P.S.)c序列
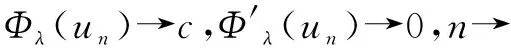
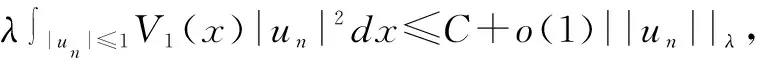
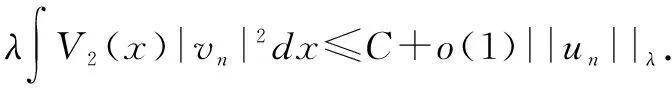
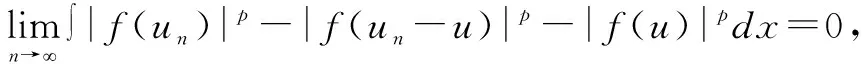
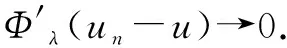
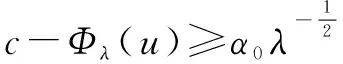
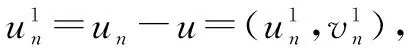


三、山路几何结构