探究式生成教学在课堂教学中的应用

涂立云

(江苏省灌南县第二中学 222500)

在某天的辅导课上，忽然间有一位学生拿着一张试卷向我走来并问到：“老师，我向您请教一个题目”.我一看标注才知道是江苏省海安高级中学高三某次模拟考试的填空题第14题.题目如下：

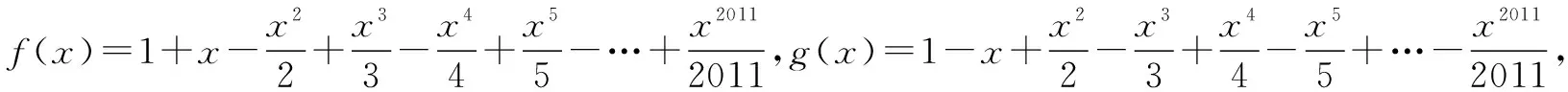
这是一道填空题的压轴题，难度可想而知.初看此题，是两个高次函数的零点问题，又是出自海安中学的高三考试压轴试题，顿感心中一片茫然，无从下手.此时一时想不到解决此题的好方法，但是又不能直接跟学生说自己不会做，该怎么办呢？心里焦虑万分，不知如何是好.当看到教室里坐着40多个学生，于是想到：如果集中大家的智慧，一起来讨论研究这个题目，也许能有意想不到的收获.于是我将题目用投影投到了黑板上，然后对讲台下的学生们说道：“同学们，这是某同学问老师的一道海安中学的试题，难度较大，老师一时还没有想到解题方法，现在我们大家一起来寻找解决此题的方法.首先请大家分析下题目的条件，你们能想到一些什么呢？”

经过5分钟的小组讨论交流，有同学站起来发言了.

生1：要求b-a的最小值，只要求出F(x)的所有零点中最小的零点和最大的零点就行了.

生2：F(x)的所有零点，即F(x)=f(x+3)g(x-3)=0的根，只需求出f(x+3)=0和g(x-3)=0的根即可.

生3：要求f(x+3)=0和g(x-3)=0的根，只需求出f(x)=0和g(x)=0的根，再分别向左和向右平移3个单位即可.

师：大家同意生1、生2和生3的分析吗？那么如何求f(x)=0和g(x)=0的根呢？本题难就难在求高次方程的根的问题.

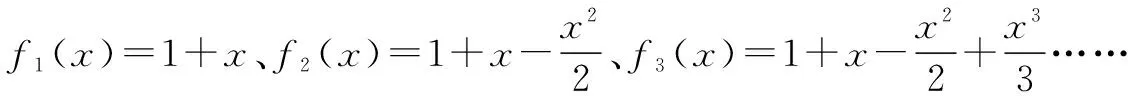
师：生4的想法符合归纳推理的思想.请同学按照他的思路试试看.

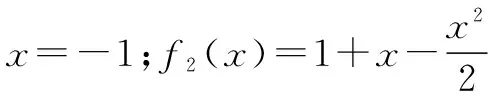
师：同学们，我们在学习用导数求曲线的切线方程时，是如何求三次方程的根的呢？比如：x3+3x2-2=0.

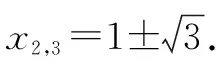
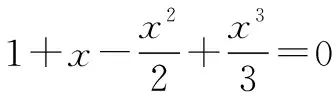
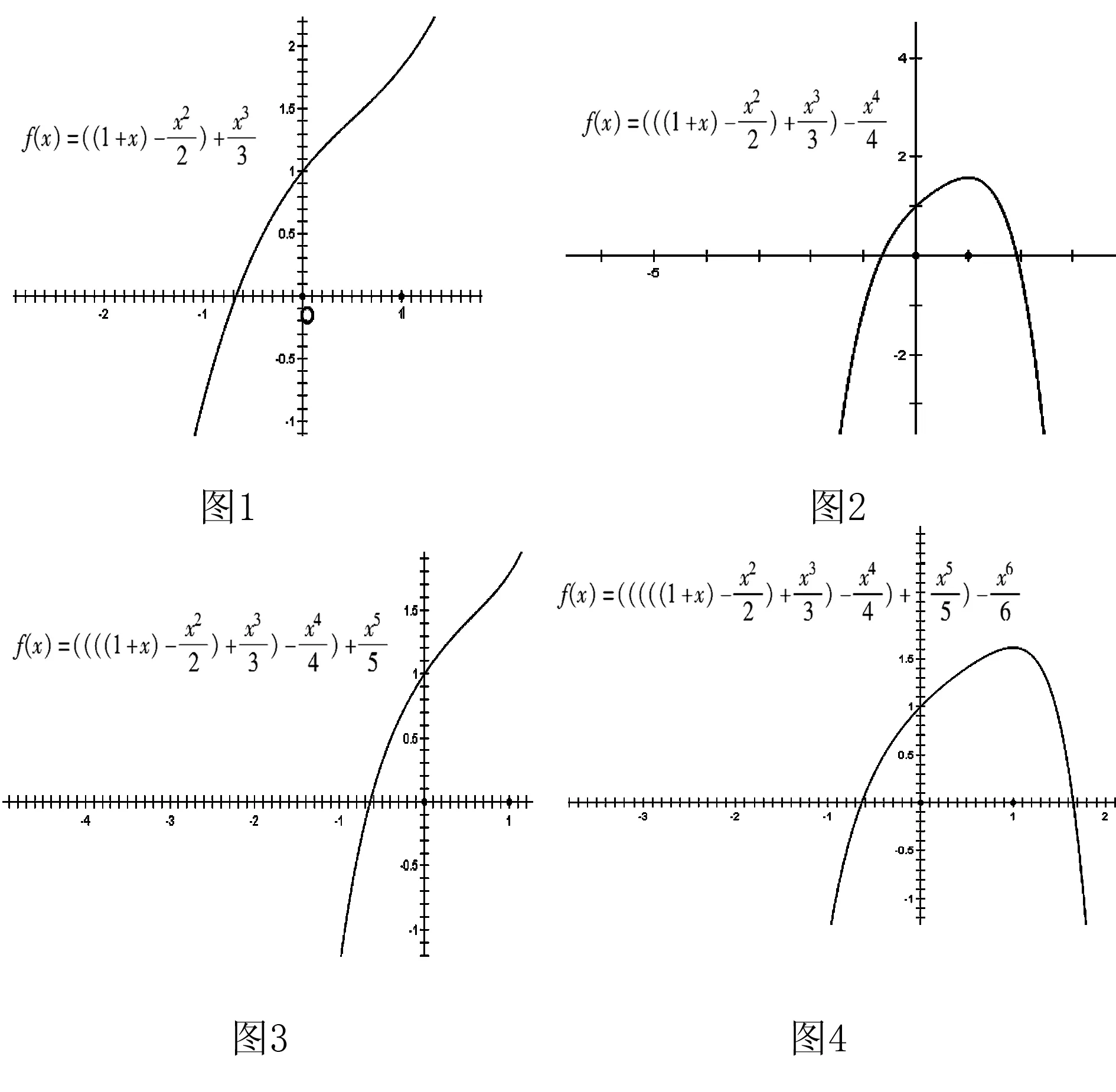
师：大家观察图形，你能得出什么结论呢？

生9：我猜测：当x的最高次数为偶数时，图形先递增，后递减，与x轴有两个不同的交点，分别在区间(-1,0)内和(1,2)内；当x的最高次数为奇数时，图形单调递增，与x轴有一个交点，在区间(-1,0)内.

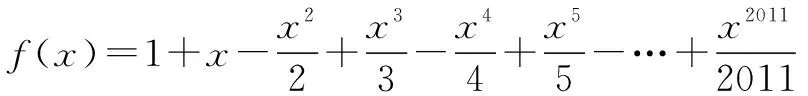
生10：可以利用导数来证明f(x)为单调增函数，利用函数的零点存在性定理来证明f(x)的零点在区间(-1,0)内.

师：好，现在我们的处理方法有了，请大家先动手试试看，再上黑板板演.

生11：f′(x)=1-x+x2-x3+x4-…+x2010(*)，再证明这个式子恒大于0，就可以了.

师：如何证明这个式子恒大于0呢？

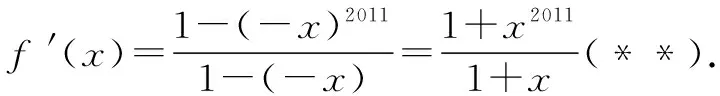
师：生12的想法很好，但是当x=0时，它不是等比数列；当x=-1时，不能用上述求和公式.

生13：当x=0时，f′(x)=1>0；当x=-1时，f′(x)=2011>0；当x<-1时，(**)式的分子、分母同时小于0，则f′(x)>0；当x>-1且x≠0时，(**)式的分子、分母同时大于0，则f′(x)>0.综上，f′(x)>0恒成立，因此f(x)为R上的单调增函数.

师：生13的讨论过程很全面.下面来证明f(x)的零点在区间(-1,0)内.

师：太棒了，现在我们已经把f(x)的零点范围确定了，那么是否可以用同样的方法来确定g(x)的零点范围呢？

生15：g′(x)=-1+x-x2+x3-…-x2010=-f′(x)<0，所以g(x)为R上的单调减函数.

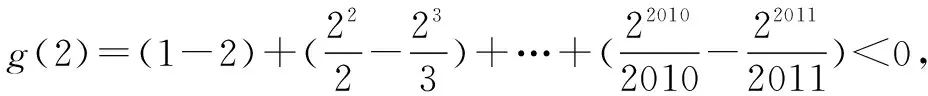
生17：所以f(x+3)=0的根在(-4,-3)内、g(x-3)=0的根在(4,5)内，则当a=-4,b=5时，b-a的最小值为9，即为所求.

数学教学是以解题为中心展开的，解题教学也是数学教学的重要环节.其功能是：培养学生运用所学知识解决实际问题的能力，在此过程中提高学生思维水平，培养独立分析问题、解决问题的能力.学生在自主探究思路的过程中，不仅仅是完成一道题目，更是宝贵的生命历程，心智的参与过程可使学生深切感知思想方法的来龙去脉.探究过程中思维的调控、优化，不仅是能力的提高，更是对学习信心的激励.教师在学生处于欲进不得欲罢不能之时，引导其改变途径，走出困境，容易使学生得到成功的快乐体验.此时学生收获的不仅是解题能力的提高，更是思维水平的提升和数学学习兴趣的激发，数学学习就会由苦变乐.