基于稚化思维理念的数学解题教学策略探究——以圆中动态问题为例

刘 雷

(江苏省苏州市吴江高级中学 215200)

一、研究背景

1.几个教学现象

在数学的解题教学中常常出现的几个现象：

现象一：教师课上题目讲评不完，未讲完的是否要讲？学生真正掌握了吗？

现象二：学生课上基本听懂，课下做题却束手无策，产生困惑；

现象三：同类题讲解多遍，学生还是经常错，感到无奈.

究其本质，这些现象产生的主要原因是课堂教学时未抓住学生的思维特点，忽视了学生作为初学者“思维幼稚”和迟缓的一面，以自己的理解方式灌输给学生，导致学生“食而不知其味”.

2.稚化思维理念

“稚化思维”是指教师在教育教学活动过程中充分关注学生原有的认知规律、知识储备、个人经验以及“最近发展区”，弱化或隐蔽自身权威，不以“专家”自居，有意识地把自己的思维水平降低到与学生相仿的思维水平，站在学生的角度设身处地地去揣摩学生的认知特点以及知识的生成过程中可能产生的障碍，力求和学生的认知与思维达到同频共振的状态.稚化思维，也可通俗理解为降低(教师)思维水平,“稚化”的对象是教师，“稚化”的目的是“智化”学生.

下面依托稚化思维理念，结合与圆有关的动态问题，来探究解题教学一般性策略.

二、策略探究

1.教师自我“稚化”，基于学生认知寻找解题突破点

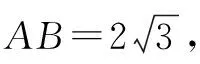
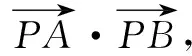
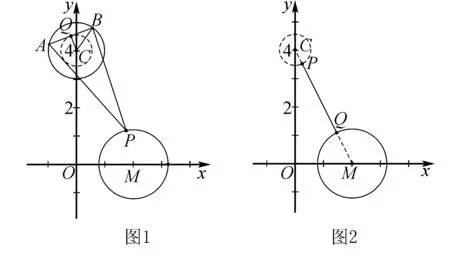
所以题目所求问题转化为求P,Q两点间距离的最小值，根据CQ=1，可得Q点轨迹是以点C为圆心，半径是1的圆，轨迹方程为x2+(y-4)2=1，而P点轨迹是圆M，所以问题转化为这两圆上的点之间的最近距离，结合图2，

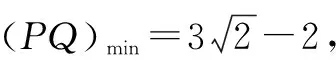
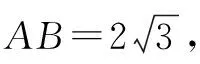
2.乘胜追击，从“稚化”教师到“智化”学生

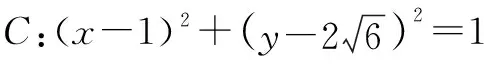
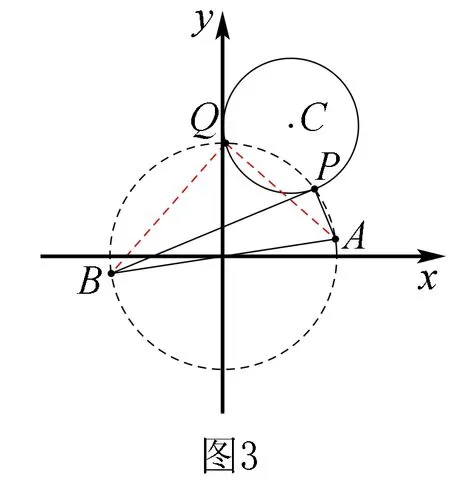
“稚化”教师的目的就是“智化”学生，首先通过例1让学生对此类问题有了初步认识和一次成功的心理体验，那么乘胜追击，通过例2让学生思维得到升华，强化此类题的解题经验和心理体验.

3.回归教材，“内化于心”

例3(苏教版必修2，P117第14题改编)已知P是直线3x+4y+8=0上的动点，PA,PB是圆x2+y2-2x-2y+1=0的两条切线，A,B是切点，C是圆心.

(1)求四边形PACB面积的最小值；

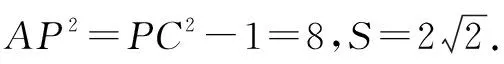
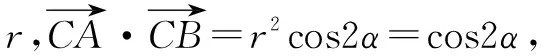
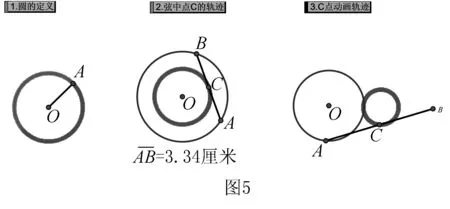
事实上，在具体的课堂教学中，根据内容可以适当利用多媒体技术或数学软件，如几何画板，Matlab等.如下图5所示的一些常见动点轨迹是圆的例子，让学生在学习之前通过直观感受，代数的严谨与几何的直观的巧妙结合.事实上，适当的结合多媒体技术对解题教学做出改善和创新，提高教学实效的同时也培养了学生的直观想象素养.

我们教师在平时解题教学中要善于利用稚化思维理念，进行有效解题教学，使学生达到做一题会一类的效果.“惑学生之所惑，想学生之所想”，多站在学生的角度思考问题，“稚化”教师思维，从而“智化”学生，提高了教学实效的同时也是从根本上把提高学生的数学核心素养落到实处.